三次函数图像的基本特点初探
段春林
【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089(2019)51-0122-01
我们把形如y=ax3+bx2+cx+d(a≠0,b,c,d∈R)的函数称为三次函数,对其图像的考查在高考命题中常常出现,有鉴于此,本文将对三次函数图像的一些特性作一初步探讨。
我们先从一个例子谈起:
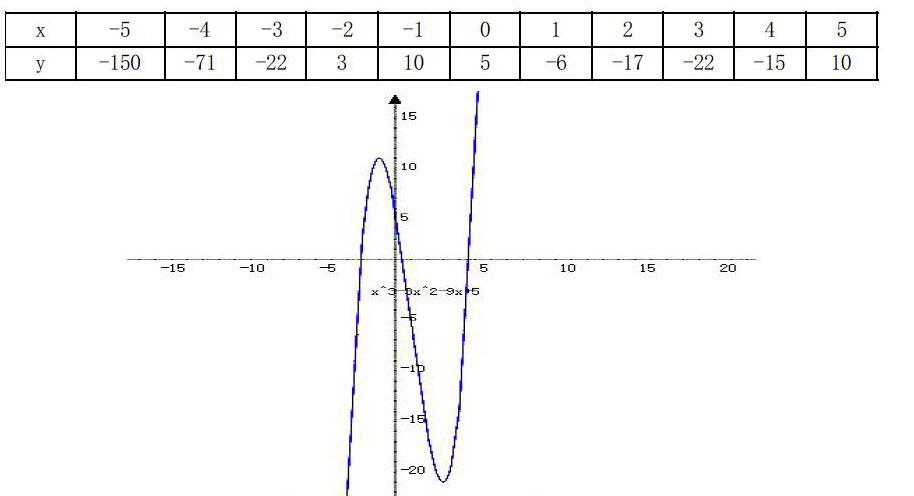
下图是y=x3-3x2-9x+5经过列表描点所画出的三次曲线。
从图中可以看出:曲线光滑且连续;
第一,从左向右看,曲线经由第Ⅲ象限而来,从第Ⅰ象限离去,这点从“优势原则”可得,优势原则可表述为:对于充分大的|x|,多项式的值取决于最高次项,即对于充分大的|x|,|x3|的值超过|-3x2-9x+5|,因此,对于充分大的|x|,由x>0推得y>0,由x<0推得y<0.
第二,此三次函数的定义域与值域均为R,是否一般三次函数都有这一结果?
第三,这个三次函数有两个极值点,极大值点(-1,10),极小值点(3,-22),这一情况可通过讨论y′得到,令y′=0,即x2-2x-3=0,得x=-1或x=3.
第四,曲线的纵截距为d=5.
第五,此三次曲线有三个零点,由零点存在性定理可知,三个根分别在(-3,-2),(0,1),和(4,5)之间,因为f(-3)=-22,f(-2)=3,f(0)=5,f(1)=-6,f(4)=-15,f(5)=10.
第六,此函数的单调区间∵y′=3(x2-2x-3)
令y′>0,得x∈(-∞,-1)∪(3,+∞),令y′<0,得x∈(-1,3),由此可知,x∈(-∞,-1)和x∈(3,+∞)时y=f(x)单调递增,当x∈(-1,3)时,y=f(x)单调递减。
第七,研究y″得到y″=6x-6,令y″>0,得x>1.
若x<1,y=f(x)为上凸函数,若x>1,y=f(x)为下凸函数,(1,f(1))是此函数图像的拐点;
第八,有对称中心,其对称中心是(-,f(-)).证明如下:
设函数y=ax3+bx2+cx+d(a≠0,b,c,d∈R)的对称中心为(m,n)。
按向量=(-m,-n)将函数的图像平移,则所得函数y=f(x+m)-n是奇函数,所以f(-x)=-f(x),即f(-x+m)-n=-(f(x+m)-n),于是f(-x+m)+f(x+m)-2n=0
化简得:(3ma+b)x2+am3+bm2+cm+d-n=0
上式对x∈R恒成立,故
3am+b=0am3+bm2+cm+d-n=0
得m=-,
n=am3+bm2+cm+d=f(-)。
所以,函数y=ax3+bx2+cx+d(a≠0,b,c,d∈R)的对称中心是(-,f(-))。
那么这个对称中心有无特殊性,即它是不是在图像的特殊位置呢?我们有了如下结论:若三次函数y=ax3+bx2+cx+d(a≠0,b,c,d∈R)有极值点(有的话,必有两个,一个极大,一个极小)(x1,f(x1))和(x2,f(x2)),则它的对称中心是两个极值点的中点(,f()).
证明:不妨设3ax2+2bx+c=0为f(x)的导函数方程,其判别式△=4b2-12ac>2.,設f(x)两极值点为A(x1,f(x1))和B(x2,f(x2)).
易知x=为y=3ax2+2bx+c的对称轴,∴f()=f(-)
故此时的对称中心是两个极值点的中点,同时也是函数 f(x)的拐点。
从以上结论可知,我们对三次函数图像的讨论主要集中在8个方面,即途经的象限、定义域、值域、有无极值、纵截距、零点个数、单调区间、拐点、对称中心。下面针对以上问题做一粗略讨论。
不妨设y=ax3+bx2+cx+d(a≠0)
∵y′=3ax2+2bx+c,y″=6ax+2b,
令y′=0(?鄢),其解的个数取决于△=4b2-12ac=4(b2-3ac)(?鄢?鄢)
令y″=0,解得x=-,此即为对称中心谈论的问题。
①若b2-3ac>0,(?鄢)式有两根,不妨设为x1、x2,y=f(x)有两个极值点A(x1,f(x1))和B(x2,f(x2)),有一拐点(-,f(-)),单调性为先单增(-∞,x1)后单减(x1,x2)再单增(x2,+∞);
②b2-3ac≤0,(?鄢)式有两等根,图像与x轴有一个交点,即有一个零点,无极值点,有一拐点,单调性为单调递增。
综上可知,三次函数y=ax3+bx2+cx+d(a≠0,b,c,d∈R)有:
①定义域和值域均为R;
②当a>0时,曲线(从左向右看)从第Ⅲ象限“进入”,经第Ⅰ象限“离开”;
③当a<0时,曲线(从左向右看)从第Ⅱ象限“进入”,经第Ⅳ象限“离开”;
④纵截距为d;
⑤曲线与x轴至少交一次(其交点个数由△和极值点的坐标综合得出,前面已讨论,不再赘述)。

