平面应力状态的解析法和应力圆法详解
陆仁强
摘要:材料力学是土木类专业学生必修的一门专业基础课,对于后续专业课程的学习具有重要的基础作用。但是材料力学由于其力学研究过程的复杂性和抽象性,使得学生在学习过程中存在较大的困难,而且感觉枯燥无味。笔者通过对材料力学课程的多年讲授,总结了一套简单易懂的教学方法,本文以“平面应力状态任意方向面上应力”的求法为例,通过例题讲述及结论分析,教学效果反思发现能够让学生很容易的理解该部分内容。本文的教学成果和方法,对于地方高校应用型专业课程的讲授具有一定的示范作用,可值得同类课程的借鉴采用。
关键词:平面应力状态;解析法;应力圆法
1 平面应力状态的概念及表示
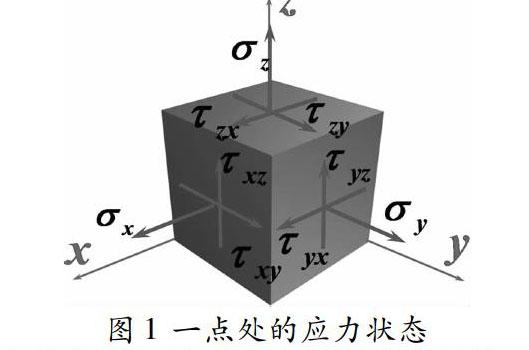
研究一个点的应力状态,通常围绕该点作一微小单元体,称为单元体,一般情形下,微元的不同方位面上的应力各不相同,用任意截面把该微元体截开,则截开面上也存在正应力和切应力,过一点处的所有方位面的应力集合,称为该点的应力状态。
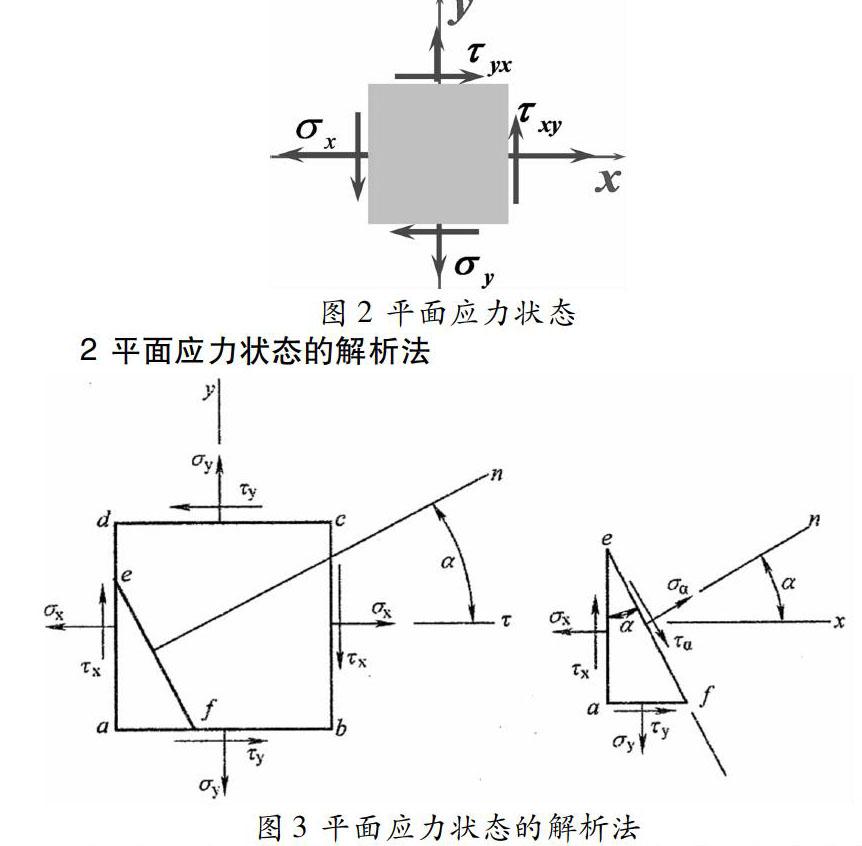
平面应力状态:微元各个面上所受应力的作用线都处于同一平面内,这种应力状态称为平面应力状态。根据立体几何知识可知,图1所示的空间应力状态要转变为平面应力状态,则σx、σy、σz三者中至少有一个为0,即(τzy、τzx)、(τxy、τxz)、(τyx、τyz)三对中至少有一对为0,由于通常习惯于用x、y平面,故假设σz和(τzy、τzx)等于0,这样,图1的空间应力状态就可以表示为图2所示的平面应力状态了。
2 平面应力状态的解析法
如图3所示,假设用任意一个截面把图中的平面应力状态截开以后,得到右边部分,截开面称为方向面,设方向面的法线方向为n。
根据微元的局部平衡,列静力学平衡方程:∑Fx=0∑Fy=0
画应力圆的技巧:1)若知道圆心坐标和半径,可画圆;2)若知道任何一条直径的两个端点也可以画圆。
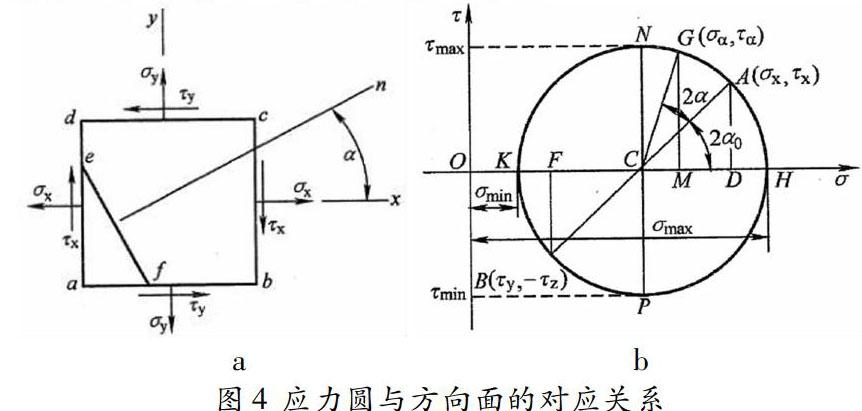
假设某应力状态为下图4a图,画出的应力圆为图4b图,也就是说图4a和图4b是等价的。下面先说明应力圆与方向面(即图4a和图4b)之间的对应关系:
(1)点面对应关系。在应力状态中指的是方向面,而到了应力圆中指的是点。比如(σx、τx),对应的是图4a中的左侧面,而对应到图4b的应力圆,找到坐标值为(σx、τx)的点为A点,也就是应力圆中的A点对应应力状态中的左侧面。同理,图4a中(σy、τy)所在的下侧面,对应到图4b应力圆中的B点。
(2)二倍角关系。图4a中的左侧面(σx、τx)和下侧面(σy、τy)为垂直关系,即夹角为90°,而到了图4b所示的应力圆中,其所对应的A点和B点却在同一条直径上,即夹角为180°,这就是所谓的“二倍角关系”,即:在应力状态中两个方向面的夹角若为α,则在应力圆中所对应的两个点所在半径的夹角将是2α。
(3)转向一致关系。在图4a所示的应力状态中,若以左侧面(σx、τx)为参考面,则下侧面(σy、τy)与之呈逆时针旋转的90°关系,对应到图4b所示的应力圆中,A点所在半径绕圆心逆时针旋转180°即到了B点所在的半径,这叫做“转向一致”,即:应力状态中两个方向面的位置与应力圆中对应的两个点的位置关系是一致的。
简记为:点面对应、转向相同、夹角两倍。
下面以例题为例说明应力圆的画法及应用:
例题在图示xy坐标系下,单元体的最大主应力σ1大致指向()。
(A)第一象限,靠近x轴(B)第一象限,靠近y轴
(C)第二象限,靠近x轴(D)第二象限,靠近y轴
解:
(1)确定应力圆的画法方式,可通过一条直径画圆,也可以通过圆心坐标及半径值画圆,本题采取第一种方式,由图可知,左侧面与下侧面呈90°,在应力圆上就恰好对应一条直径上的两个端点;
(2)已知左侧面上的应力值(σx>0、τ<0),在应力圆坐标系上找到相应坐标点设为A点,已知下侧面上的应力值(σy<0、τ>0),在应力圆坐标系上找到相应坐标点设为B点;
(3)连接AB点便得到应力圆的一条直径,将该直径绕中点转一圈便可得到应力圆,如图。
通过应力圆可得到的一些信息:
应力圆与横坐标轴的两个交点C、D对应的方向面即为主平面(因为其切应力τ=0),左边交点C的正应力对应最小主应力σ3,右边交点D的正应力对应最大主应力σ1。
根据上述应力圆可知,从A点逆时针转到最大主应力σ1所对应的D点,转动的角度肯定小于90°,而对应到应力状态中就肯定小于45°(根据二倍角关系)。故可得答案选A(注:题目问的单元体的最大主应力σ1大致指向,指的是最大主应力σ1所在的方向面的方向角)。
4 总结
本文以“平面应力状态的解析法和应力圆法”为例,通过例题讲解了应力圆法的绘制及应用解题的具体过程。该教学方法通俗易懂,没有太多的理论讲授,将理论贯穿于例题讲解的过程中,学生听起来不觉得枯燥乏味,也简单易懂。故本文提出的教学方法值得同类地方本科院校应用型课程的教学借鉴和推广采用。
参考文献:
[1]郭志昆,陈万祥,郭伟东,等.应力圆的解析与图解法证明[J].力学与实践,2016,38(5):581586.
[2]王云侠.平面应力状态下主应力与主平面的对应关系的探讨与研究[J].科技信息,2007,(35):531533.
[3]董春亮,卢小雨.平面应力状态分析的一种新方法[J].攀枝花学院学报,2015,32(2):7072.
[4]许杨剑,阮洪势,沈倩倩,等.材料力学教学中的编程实践——应力状态分析[J].力学与实践,2018,40(4):446450.
基金项目:2016年湖南科技学院教学改革研究项目“基于‘卓越工程师培养的‘大土木专业《理论力学》課程改革与实践”

