以一道课本习题为例谈阿波罗尼斯圆

■甘大旺

人教A版高中数学②的第124页习题4.1B组第3题∶已知点M与两个定点O(0，0)，A(3，0)的距离的比为1∶2，求点M的轨迹方程。

解法1：设动点M的坐标是(x，y)，则依题意得整理得x2+y2+2x-3=0。经检验，点M的轨迹方程是(x+1)2+y2=4。

解法2：①当点M在直线OA上时，由于，则动点M恰有两个位置M(1，10)，M2(-3，0)适合②当点M不在直线OA上时，由于，则 MM、MM分别是∠OMA 的12内、外角平分线，故MM1⊥MM2，则M在以M1M2为直径的圆上。

由①②可知，点M的轨迹是以线段M1M2的中点O'(-1，0)为圆心，以为半径的圆(如图1所示)，所以点M的轨迹方程是(x+1)2+y2=4。

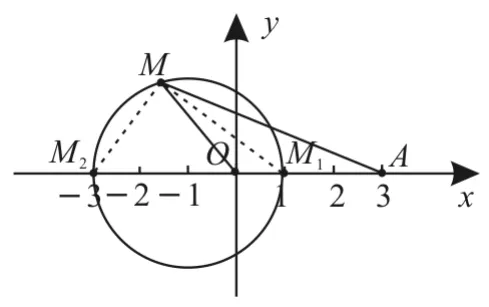
图1

反思：解法1运用直接求轨迹法，简洁快速;解法2运用几何求轨迹法，虽然解题过程稍长，但却能够自然而然地引导我们揭示这道课本习题的数学史背景——阿波罗尼斯圆。阿波罗尼斯是古希腊亚历山大早期的三大数学家之一(前两位是欧几里得和阿基米德)，仅凭一部巨著《圆锥曲线论》就使得古希腊几何学在世界数学史上登峰造极，而至少领先1500年。阿波罗尼斯发现了一个流传至今的结论∶“平面上到两个定点的距离之比等于定值(且该定值不为1)的动点轨迹是一个圆”。后来，数学界把这个圆称为阿波罗尼斯圆。

探索：在共线的顺次四点 M1(1，0)，M2(-3，0)，O(0，0)，A(3，0)中，已有等式，验证知由此我们可知，到两点M，1M2的距离之比为1∶3的动点N的轨迹方程是以线段OA为直径的圆，故圆的方程为(如图2所示)。

图2

发现：抽象思考上述解法2，尝试探索，不难提炼出一个概括结论，即定理1。

定理1：已知平面内在同一条直线上的顺次四点A，P，B，Q满足两个等式

(1)在该平面内到两点A，B的距离之比等于定值λ的动点M的轨迹是以线段PQ为直径的阿波罗尼斯圆。

(2)在该平面内到两点P，Q的距离之比等于定值μ的动点N的轨迹是以线段AB为直径的阿波罗尼斯圆。

验证：(1)(2)类似于上述解法2(过程略)。(3)如图3，不妨设四点A，P，B，Q顺次在x轴上，并用一维坐标分别标记为A(0)，P(p)，B(b)，Q(q)，由于λ，则，即(等比定理)(合分比定理，反比定理)，则，故解得

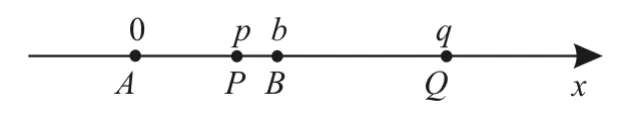
图3

定理1中的(1)(2)蕴含着两个相伴阿波罗尼斯圆的直径画法;反之，平面上任意两个相交圆是不是这种相伴的阿波罗尼斯圆呢?定理1中(3)的比值范围给予了否定。

除上述例题外，人教A版高中数学②还有两道涉及阿波罗尼斯圆的习题，分别是第4.3节140页“信息技术应用”的例题，144页第4章复习参考题的B组第2题。

下面再提供两道相关的跟踪练习题。

跟踪练习1：在△ABC中，AB=2AC，角A的平分线AD交BC于点D，且AD=kAC，△ABC的面积等于1，问∶当k为何值时BC最短?

审题方法：点D以分比为2内分线段BC，作其外分点E，则到两点B，C的距离之比等于定值2的动点A在以线段DE为直径的阿波罗尼斯圆上。

解题思路：单纯着眼于三角形的边角关系，可以选用三角法;着眼于转化为阿波罗尼斯圆问题，可以选用解析法。

解法1：根据cos∠CAB=cos2∠CAD，BD=2BC，运用余弦定理解答(过程略)。

解法2：依题意，记AB=2AC=2b，AD=kAC=kb。根据三角形的内角平分线定理，得则AD=2DC以分比作线段BC的外分点E，则到两点B，C的距离之比等于定值2的动点A在以线段DE为直径的阿波罗尼斯圆上，如图4所示。

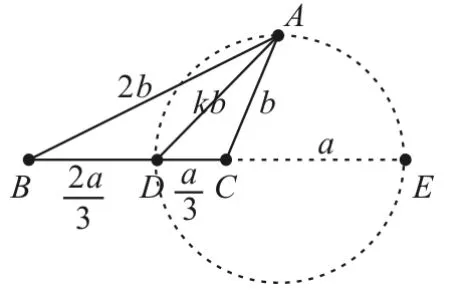
图4

再取该阿波罗尼斯圆的圆心O为原点，直线BE为x轴，建立平面直角坐标系xOy，则该阿波罗尼斯圆O的方程是x2+y2=依题意得则，代入圆O的方程得0，解得a2≥3。验证知当xA=0时，BC=a取最小值 3，此时，OA⊥DE，则所以，当时，BC最短。

变式训练1：已知点P到两个定点M(-1，0)，N(1，0)的距离之比为 2，点 N到直线PM的距离为1，求直线PN的方程。

提示：到两个定点M(-1，0)，N(1，0)的距离之比为2的阿波罗尼斯圆是(x-3)2+y2=8，直线PM的倾斜角为30°或150°，求得直线PN的方程是x±y-1=0。

变式训练2：正方形ABCD内部的一点P满足AP∶BP∶CP=1∶2∶3，求∠APB。

提示：先用阿波罗尼斯圆方程，后用余弦定理，也可单独用余弦定理，不妨设正方形的边长为1，最后求得∠APB=135°。

跟踪练习2：已知两点A(-2，0)，B(2，0)，点P满足，且PB⊥AB。试在x轴上寻找一点M，使得AP⊥PM。

审题方法：点P在到两点A，B的距离之比等于定值3的阿波罗尼斯圆上，考虑已知直角∠ABP=90°和目标直角∠APM=90°。

解题思路：把零散条件拼凑起来，运用方程组解答;巧妙转化，运用阿波罗尼斯圆。

解法1：设点M为(m，0)，解方程组(过程略)。

解法2：在直线AB上以分比λ=3找到线段AB的内分点P1(1，0)，P2(4，0)，则点P在阿波罗尼斯圆上，且满足PB⊥AB，如图5所示，该圆的圆心为。设点M为(m，0)，使得AP⊥PM，则由直角三角形中的射影定理，得即(-2)]·(m-2)，化简得2=4(m-2)，解得所以在x轴上寻找到的点M为，符合题意。

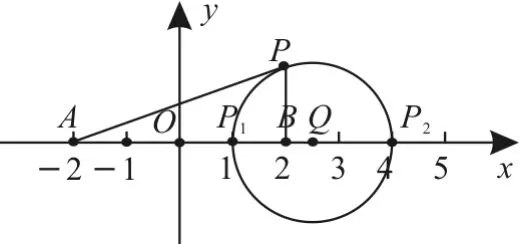
图5

发现：这里求出的点M重合于圆心，于是我们又可以提炼出一个概括结论，即定理2。

定理2：在平面上，线段AB以定值λ(大于1)为分比的内外分点分别为P1，P2，以线段P1P2为直径作阿波罗尼斯圆Q，作该圆Q的弦P3P4，则连线AP3，AP4是圆Q的两条切线。

变式训练3：验证定理2。

提示：可用解析法，用到定比分点坐标公式(过程略)。

变式训练4：如图6，过点A(-2，-1)作圆Q∶(x-2)2+(y-1)2=4的两条切线AT1，AT2，切点弦T1T2与连线AQ交于点H，圆Q与连线AQ交于点B，C，连接T2C。

图6

(1)求证∶T2C是∠AT2H的外角平分线。

(3)过点A作圆Q的割线与圆Q交于点M，N，与切点弦T1T2交于点D，试探究等式是否恒成立。

提示：则所以故TC是∠ATH的外角平分线。

(3)设割线MN的点斜式方程为y+1=k(x+2)，与圆Q的方程联立，消去y并整理成关于x的二次方程，用到韦达定理。T1T2⊥AQ，可求出连线T１T２的12方程是2x+y-3=0。由等式(xM+xN)+2·xMxN=4·xD。代入检验，等式恒成立。

说明：定理、跟踪练习与变式训练不但以阿波罗尼斯圆为数学史背景，同时还孕育着极点、极线、调和点列的萌芽，同学们在学习之余请多思考这几道题的特点。