一类左欧拉余代数及其欧拉双线性型

唐 帅

(泰州学院数理学院，江苏 泰州 225300)

0 引言

文献[1]针对基本余代数提出了左欧拉余代数的概念.基本左欧拉余代数相对于基本余代数而言具备一些特殊的性质.比如：在基本左欧拉余代数上可以研究类似于基本代数所具有的欧拉双线性型、Coxeter变换等内容；[1-2]当C是基本左欧拉余代数时，任意两个有限维左C-余模可以配成欧拉对[1]；在基本左欧拉余代数上可以定义并研究所谓的欧拉余模[3]等.目前许多基本余代数具有基本左欧拉余代数结构.比如：当C是基本的有限维余代数并且整体维数有限时，C是左欧拉余代数[1]；当C是右半完全余代数并且C的每一个单余模的内射维数有限时，C也是左欧拉余代数[1].有关左欧拉余代数上的相关结果可参见文献[1-4].

对秩为1的点Hopf代数的研究已经取得了许多结果.文献[5]给出了这类Hopf代数的分类，其分类结果可以追溯到文献[6]；文献[7]将这类Hopf代数的分类结果由有限维特征0的情形推广到无限维任意特征的情形，并研究了这类Hopf代数的模范畴中一类重要的对象——权模；文献[8-9]从Green环角度研究了这类Hopf代数的表示范畴的Monoidal结构.

本文主要研究一类秩为1的点Hopf代数H的余表示.利用Hopf代数H是基本余代数这一事实给出了同构意义下所有有限维不可分解左H-余模；完全刻画了任意两个不可分解左H-余模之间的余模态射空间，并据此回答了何时Hopf代数H作为余代数是左欧拉余代数；当H是左欧拉余代数时，给出了H的欧拉双线性型、欧拉二次型以及对应的Coxeter变换等结果.

1 预备知识

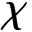
H作为余代数，余乘△与余单位ε定义为

△(x)=ɡ⊗x+x⊗1，△(a)=a⊗a，ε(x)=0，ε(a)=1，∀a∈G.

H的对极S定义为S(x)=-ɡ-1x，S(a)=a-1，∀a∈G.

显然{axi|a∈G，0≤i≤n-1}构成H的一组K-基.记Hi=KG⨁KGx⨁…⨁KGxi，0≤i≤n-1，则H0⊂H1⊂…⊂Hn-1为H的余根滤链.对k用数学归纳法容易证明

(1)

设M(a，i)=sociEa，其中a∈G，1≤i≤n.因为H是单列余代数[10]，H的任意有限维不可分解左H-余模形如sociEa[11]，其中1≤i≤n，a∈G.因此，集合{M(a，i)|a∈G，1≤i≤n}构成同构意义下所有有限维不可分解左H-余模.显然{a，ax，…，axi-1}为M(a，i)的一组K-基，并且不可分解余模M(a，i)由其基座Sa与向量空间维数i唯一决定.

2 左欧拉余代数

左H-余模M到N的余模映射的全体记为HomH(M，N).对于任意两个不可分解余模M与N，本文刻画了余模映射空间HomH(M，N)的维数，利用这一结果回答了何时H作为余代数是左欧拉余代数.

引理1对于任意a∈G，1≤k≤j，有商余模同构M(a，j)/M(a，k)≅M(aɡ，j-k).

soc(M(a，j)/M(a，k))=M(a，k+1)/M(a，k)≅Saɡk.

比较维数有M(a，j)/M(a，k)≅M(aɡk，j-k).

命题1(1) 对于任意a，b∈G，1≤i≤j≤n，有

(2) 对于任意a，b∈G，1≤j≤i≤n，有

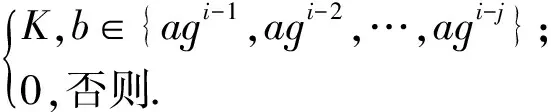
证明(1) 设α为M(a，i)到M(b，j)的非零左H-余模映射，则kerα为M(a，i)的子余模.注意到M(a，i)是单列余模，M(a，i)的所有真子余模在包含关系下形成子余模的序列0⊂M(a，1)⊂…⊂M(a，i-1).因而kerα∈{0，M(a，1)，…，M(a，i-1)}.由引理1知，商余模M(a，i)/kerα在同构意义下具有如下形式：

M(a，i)/kerα∈{M(a，i)，M(aɡ，i-1)，…，M(aɡi-1，1)}.

(2)

然而M(a，i)/kerα≅Imα⊆M(b，j)，因此Sb=socM(b，j)=socImα=soc(M(a，i)/kerα).此时结合(2)式可得Sb∈{Sa，Saɡ，…，Saɡi-1}，这就证得b∈{a，aɡ，…，aɡi-1}.为了证明当b∈{a，aɡ，…，aɡi-1}时，有向量空间同构HomH(M(a，i)，M(b，j))≅K，假设b=aɡk，其中0≤k≤i-1.注意到存在如下的从M(a，i)到M(aɡk，j)的余模映射φ：

其中：π为典范投射，ι为包含映射，中间的同构为相差一个非零常数的恒等映射(这是因为对于任意不可分解余模M，EndH(M)≅K).设β为M(a，i)到M(aɡk，j)的任意非零余模映射.类似于映射α的分析，有M(a，i)/kerβ≅M(aɡk，i-k)，因而kerβ=M(a，k).此时映射β有如下分解：

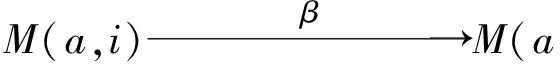
这就证明了β与φ仅仅相差一个非零常数，从而HomH(M(a，i)，M(b，j))≅K.

(2) 设α为从M(a，i)到M(b，j)的非零余模映射，因为

M(a，i)/kerα≅Imα∈{M(b，1)，M(b，2)，…，M(b，j)}，

故dimK(kerα)∈{i-1，i-2，…，i-j}.注意到soc(kerα)=socM(a，i)=Sa，因而

kerα∈{M(a，i-1)，M(a，i-2)，…，M(a，i-j)}.

(3)

由(3)式推出

M(a，i)/kerα∈{M(aɡi-1，1)，M(aɡi-2，2)，…，M(aɡi-j，j)}.

(4)

而Sb=socM(b，j)=socImα=soc(M(a，i)/kerα)，故(4)式表明b∈{aɡi-1，aɡi-2，…，aɡi-j}.若b=aɡi-k，其中1≤k≤j，类似于结论(1)的分析，余模映射空间HomH(M(a，i)，M(aɡi-k，j))为映射

M(a，i)→M(a，i)/M(a，i-k)≅M(aɡi-k，k)⊆M(aɡi-k，j)

生成的向量空间，因而HomH(M(a，i)，M(aɡi-k，j))≅K.

推论1对于任意a，b∈G，有：

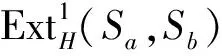
证明将函子HomH(Sa，-)作用于短正合列

0→Sb→Eb→Eb/Sb→0，

(5)

可得正合列

结合命题1可知

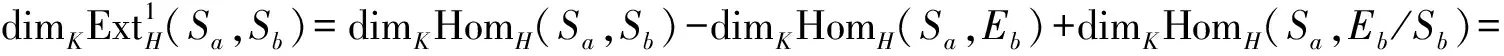
(2) 证明与上面类似，将短正合列(5)换为短正合列0→M(b，n-1)→Eb→Eb/M(b，n-1)→0即可.

定理1若群G的中心元ɡ是无限阶的，则H作为余代数是左欧拉余代数，即H满足左欧拉余代数的如下定义条件：

(1) 对于任意a，b∈G，HomH(Ea，Eb)总是有限维的；

(2) 任意单H-余模Sb具有内射分解

使得该内射分解中每一个内射余模都是基座有限的，并且对于任意不可分解内射余模Ea，总存在某个与Ea相关的正整数k使得

HomH(Ebɡjn，Ea)=HomH(Ebɡjn+1，Ea)=0，∀j≥k；

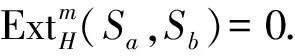
证明结论(1)可由命题1得到.

(2) 根据引理1，有如下短正合列：

0→Sb→Eb→M(bɡ，n-1)→0，

0→M(bɡ，n-1)→Ebɡ→Sbɡn→0，

⋮

0→Sbɡkn→Ebɡkn→M(bɡkn+1，n-1)→0，

0→M(bɡkn+1，n-1)→Ebɡkn+1→Sbɡ(k+1)n→0，

⋮

这就得到Sb的内射分解

(6)

显然，对于任意内射余模Ea，由命题1知存在某一k使得对于所有j≥k，

HomH(Ebɡjn，Ea)=HomH(Ebɡjn+1，Ea)=0.

(3) 对于Sb的内射分解(6)，由同调代数基本结论可知

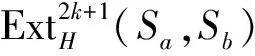
并且

因为ɡ的阶无限，对于任意a，b∈G，由推论1知最多存在一个k1使得

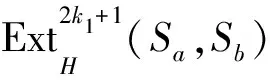
同时最多存在一个k2使得

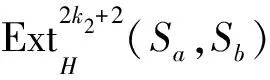
注1(1) 如果ɡ的阶有限，则ɡ的阶能够被n整除[7].此时H不是左欧拉余代数，这是因为在Sb的内射分解(6)中，内射余模都是周期呈现的，此时定理1中的结论(2)与结论(3)不再成立.

(2)Sb的第m-次余合冲定义为ΩmSb=Imdm-1，其中dm-1为Sb的内射分解(6)中的态射.对于任意k≥0，容易推出Ω2kSb=Imd2k-1=Sbɡkn，Ω2k+1Sb=Imd2k=M(bɡkn+1，n-1).

3 欧拉双线性型

类似于基本代数Cartan矩阵的定义，Hopf代数H作为余代数其Cartan矩阵定义为无限阶矩阵C=(cij)i，j∈Z，其中cij=dimKHomH(Ei，Ej)，即Sj在合成列Ei中的重数[1].由命题1可知，当j∈{i，i+1，…，i+n-1}时，cij=dimKHomH(Ei，Ej)=1；否则cij=0.因此Cartan矩阵C为无限阶上三角矩阵：

(7)

由文献[1]可知，H作为基本左欧拉余代数其Cartan矩阵C是左可逆的，即存在矩阵C-1使得C-1C=E，其中E为单位矩阵.且矩阵C-1可以写成如下形式：

(8)

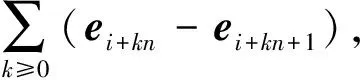
注意到向量乘积

因此，矩阵C-1也是Cartan矩阵C的右可逆矩阵，即CC-1=E.

证明(1) 注意到Hopf代数H的欧拉双线性型定义为Z-双线性型

b：ZZ×ZZ→Z，b(x，y)=x(C-1)TyT，

其中x，y∈ZZ.根据(8)式中矩阵C-1的表示形式，有

(2) 注意到Hopf代数H的欧拉二次型定义为

q：ZZ→Z，q(x)=b(x，x)，

其中x∈ZZ.由结论(1)可得结论成立.

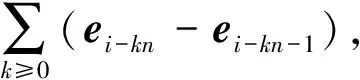
因此，当i=j-n+1时，矩阵Φ=-(C-1)TC中的(i，j)-元为-1；否则为0.因而矩阵Φ可以写成如下形式：

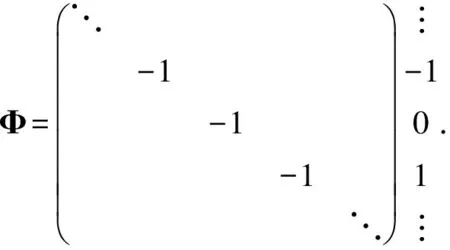
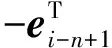
即Φ((xi)i∈Z)=(-xi-n+1)i∈Z.