基于迭代插值法的全井周电成像图像修复方法

彭 湃

(长江大学 地球物理与石油资源学院，湖北 武汉 430100)

0 前 言

电阻率成像测井能够得到井眼周围的二维电阻率图像，该图像能较为清晰和直观地反映井周的地层构造和结构特征。利用其图像的直观性和可视性，能有效的处理常规测井难以解决的问题[1-3]。但由于井径大小以及电阻率成像测井仪器结构上的特点，当仪器测量处于张开状态时，无法做到100%全井眼覆盖，各极板之间存在空白区域，导致了在电阻率测井图像上存在多个白色条带，不利于后续的图像处理与地质现象的识别。

电成像空白条带填充属于图像修复，即利用图像中已有的信息去修复图像中未知部分[4]。从数学角度看，图像修复是一个病态问题，没有足够的信息保证修复结果是唯一正确的，只能从修复后的图像是否接近或达到原图的视觉效果来评价修复的效果[5]。关于图像空白带的修复，前人已经开展了大量的研究[6-10],图像修复方法一般分为基于纹理合成的图像修复方法和基于结构的图像修复方法[11]。基于结构的修复算法主要是插值算法，例如反距离加权插值法，这也是应用最多、处理速度最快的一种插值算法。针对电成像空白条带的修复，康晓泉等[12]利用空白区域之间相邻极板的电阻率值对空白区域进行插值，实现了空白区域的信息填充。葛仕明等[13]提出了一种结合灰度和梯度方向的图像修复方法，得到了较好的电导率图像的平滑插值结果。孙建孟等[14]采用反距离加权插值和多点地质统计学方法，对斯伦贝谢公司FMI电导率图像数据进行了插值填充，获取了高质量的图像。插值算法原理简单、处理速度快，但是经反距离加权插值算法修复后的图像都还存在着明显的处理痕迹，即台阶现象，整体视觉效果不一致。

本文是以斯伦贝谢FMI电成像测井数据为例，结合FMI电成像测井仪器的结构特征，分析了经过传统反距离加权插值法修复后的图像易出现台阶现象的原因是传统插值方法在充填较宽空白带时没有考虑到影响点与待插值点间距离较远而带来的预测误差。我们针对该原因对传统方法做了改进，提出了基于迭代型反距离加权插值法的图像修复技术。该方法通过改变插值顺序，将已插值点添加为新的影响点进行插值，极大地利用了已插值点的影响，减少了影响点与待插值点间的距离，因此降低了由于影响点与待插值点距离较远而带来的预测误差；同时相当于增加了影响点的个数，使得修复结果更合理。并考虑到了电成像测井图中地质体大多具有横向展布的特征，在对空白带插值过程中同时加上横向上的均值平滑方法，使得修复后的图像更具有视觉一致性。将以上两种方法相融合，获得最终的修复成果图，对比于传统方法的处理结果，认为改进后的方法修复效果更好。

1 反距离加权插值法

1.1 反距离加权插值法原理

反距离加权插值法(IDW)是基于Tobler定理提出的一种插值方法，也称为距离倒数乘方法，属于一种加权插值法[4]。其原理是通过计算未测量点附近各个已知点的测量值的加权平均来进行插值。根据空间自相关性原理，在空间上越靠近的点其值就越接近，则其在最近待插值点处取得的权值就越大。因此IDW在邻近范围内插值误差对空间位置有着较强的依赖关系[15-16]。一般的表达式为：

(1)

式中，Z0为O点(待插值点)的估计值；Zi为影响点i的Z值；di为影响点i与点O间的距离；n为在估算中用到的控制点数目；r为指定的幂参数。定义每个影响点的权重为：

(2)

式(2)中λk为每个控制点的权值。

1.2 实现过程

1.2.1 计算插值区域宽度

针对实测电成像测井图像进行空白区域修复时，需要根据井径确定极板之间的空白区域。以FMI电成像测井资料为例，FMI仪器共有八个极板，分为四个主极板和四个副极板。图1为A井不带方位角的砂岩地层油基泥浆井中电成像测井原始图像。由图1可以看到，图中空白带分为宽窄不一的两类。根据A井的井径确定同一测量臂上的主极板与副极板之间的空白区域为3个像素点，即图中较窄空白带；不同测量臂的极板之间的空白区域为15个像素点，即图中较宽的空白带。采用传统的反距离加权插值法对图中两类空白区域进行修复。

图1 不带方位角砂岩地层油基泥浆井中电成像测井原始图像

1.2.2 选取影响点

在插值过程中，插值点受周围实测点的影响。以宽空白带(15个像素点间距)为例，选取空白道两侧3列(共6列)及插值点所在行上下2行(共5行)的实测点作为其影响点。如图2所示，为影响点选取示意图。图中A点为待插值点，B点为其影响点。沿图中箭头方向依次计算完中间行的插值点的值之后(即图中第3行)，滑动窗下移一个采样间隔，继续对窗口中间行进行插值。

图2 影响点选取

1.2.3 确定影响系数

将图2中所有点写成矩阵形式：

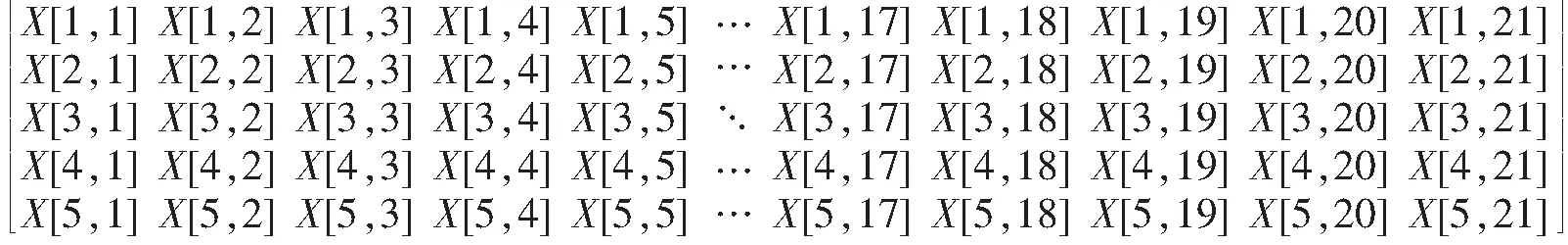
计算每个影响点到插值点的距离，例如X[1，1]到X[3，4]的距离为：

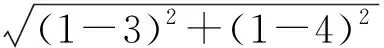
每个影响点对插值点的贡献不同，在计算权值时采用反距离加权法。根据公式(2)，权值的大小与影响点与待插值点的距离有关，是距离的r次方的倒数，根据实验经验r一般取2效果最好。则权值的公式为：

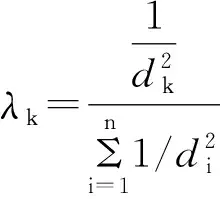
(3)

式中，dk为第k个影响点到待插值点的距离。

1.3 处理结果

处理结果如图3所示。图3(a)为不带方位角的电成像测井原始图像，图3(b)为采用传统反距离加权插值法填充后的图像。经过插值后的空白道虽然得到了消除，但是在极板与插值条带过渡区会出现明显的台阶现象，如图3(b)中4个箭头所指示位置，可见4条明显台阶线。可以看出在宽空白条带处均会出现明显的台阶现象，而窄空白条带处则不会出现，填充效果较好。针对这个问题，以及联系反距离插值法的原理，我们推测在宽空白条带处会出现台阶现象的原因是由于影响点距离插值点较远，导致预测的插值点的值不准确，从而在每个宽空白带处出现了明显的台阶现象；相反，在窄空白带处，插值法所带来的预测误差很低，修复效果相对较好。

图3 反距离加权插值法填充空白道前后图像对比

2 迭代型反距离加权插值法

2.1 迭代型反距离加权插值法原理

针对第一节中传统反距离加权插值法存在的问题，我们引入迭代型插值方法。以传统插值法为基础，改变其插值顺序，将每一个已插值点迭代入公式(1)中作为新添加的影响点，去重新估算离该点最近的插值点，依次重复，直到将空白带填充完整。在改进后的迭代型反距离加权插值方法中，充分利用了已插值点的影响，减少了影响点与待插值点间的距离，因此降低了由距离较远导致的预测误差；同时相当于增加了单个滑动窗中影响点的个数，使得估计值更加合理。

插值点的选取顺序示意图如图4和图5所示。图4中A点为待插值点，B点为影响点。首先在全井段下对图4中箭头指示方向的两列空白像素点进行插值，待该两列插值完成后得到图5所示结果(A点为已插值点，C点为待插值点)。在迭代算法中，将图5中已插值的A点作为新添加的影响点，迭代入公式(1)中进行计算插值，C插值点的插值顺序如图5中箭头指示方向。这样依次迭代插值，直到整个空白带处被充填完整。

图4 插值点选取示意图1

图5 插值点选取示意图2

2.2 横向上的均值平滑方法

考虑到在电成像测井图中地质体大多具有横向展布的特征，因此在通过迭代插值法计算完待插值点的值之后，再对计算结果做横向上的均值平滑处理，会使得过渡带更加平滑，修复后的图像更具有视觉一致性。本文中选取待插值点和待插值点左边第一个影响点作为中值平滑的参数。

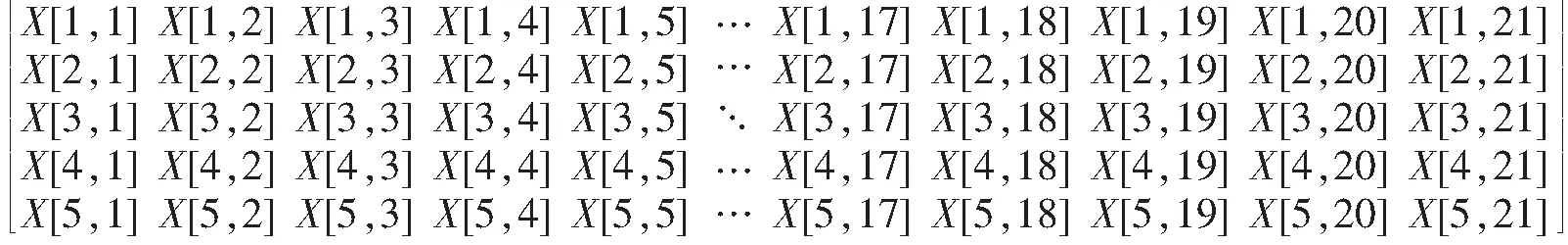
以点[3，4]为例，横向中值平滑后的结果为：

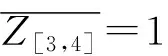
(4)

2.3 处理结果

将迭代型反距离加权插值法和横向上的均值平滑方法相结合，对空白带进行填充，处理结果如图6所示。

图6(a)为不带方位角的电成像测井原始图像，图6(b)为采用迭代型反距离加权插值法填充后的图像。可以看出经过填充后的宽空白条带和窄空白条带都得到了很好的消除，并且与原始极板有着较好的连续性。

3 处理结果对比分析

图7显示了采用不同方法进行图像修复处理的结果。图7(a)为不带方位角的电成像测井原始图像，极板之间空白区域较大。采用传统的反距离加权插值法对图7(a)所示的空白区进行插值，结果如图7(b)所示，在图中4个箭头指示处，存在四

图6 迭代反距离加权插值法填充空白道前后图像对比

条明显的台阶线。采用改进后的迭代型反距离加权插值法对图7(a)所示的空白区域进行插值，结果如图7(c)所示。对比修复后的结果图7(b)、图7(c)可以看出，采用迭代型反距离加权插值法修复后的图像较好的消除了台阶现象，修复后的图像中裂缝完整，不存在明显的台阶线，在视觉效果上都具有很好的一致性。

图7 采用不同修复方法得到的结果对比

4 结 论

1)经过传统反距离加权插值法修复后的图像在较宽的空白带处易出现台阶现象,影响了图像效果，不利于后续的图像处理和地质现象的识别；

2)传统反距离加权插值法修复的图像出现台阶现象的原因是IDW方法在邻近范围内插值误差对空间位置有着较强的依赖关系，当修复较宽的空白条带时，影响点距离插值点较远，导致预测的插值点的值不准确，从而在较宽空白条带处易出现台阶现象；

3)采用改进后的迭代型反距离加权插值法修复的图像中，空白带得到了很好的填充，同时台阶现象也得到了较好的消除，修复区与前后极板保持了很好的连续性，因此证明了该方法的正确性；

4)电成像空白条带填充后，有效的改善和提高了图像质量，更有利于后续成像图像的处理以及地质现象的识别。