基于量子神经网络的超深层储层评价*

李建平 梁胜松 范友贵

（1.东北石油大学计算机与信息技术学院 大庆 163318）（2.中国石油吉林油田公司 松原 138000）

1 引言

近年来，我国工业发展迅速，伴随着油气资源的需求也在日益增加，国内重要油田区块的开发已经进入中晚期［1］。为了提高石油采收量，国内科学家在油气勘探技术上不断向深层、超深层领域展开研究。对深层、超深层有利储层进行有效识别，是未来几年国内油气田勘探开发研究中所要解决的一个重点和难点问题，目前常用的方法需要通过勘探测井获取大量测井资料数据，然后通过专业人员对其进行分析才能判别。所以，研究出一套效率高、适应性强的算法，构建出可对储层进行定量定性分析的深层、超深层储层评价模型，对于提高油气田开发水平具有重要意义。

在当前国内外的人工神经网络领域，将量子计算和神经网络相结合的量子神经网络的已经成为了一个前沿课题。1995年，美国Louisiana大学Kak教授首次提出量子神经计算的概念在其发表题为“On Quantum Neural Computing”的论文中［2］。2000年，日本的Matsui等提出了基于量子比特描述的量子神经元模型［3］；2001年，俄罗斯的Altaisky基于量子信息处理原理提出一种量子神经网络模型［4］；2010年，巴西学者Adenilton在神经网络研讨会中首次提出一种量子无权神经网络模型，该模型基于概念量子记忆理论［5］，并设计了基于Grover搜索的学习算法［6］。2014年，日本学者Kazuhiko等提出了一种多层量子神经网络控制器，其主要基于实数遗传算法的训练［7］。国内对量子神经网络的研究也在日益加深，先后分析和改进量子神经网络模型［8］，提出了量子M-P和感知器的网络模型［9］，之后又相继提出了连续变量相干态量子神经网络模型［10］、衍生量子神经网络模型［11］和采用受控门Hadamard门构造输入为多维离散序列的量子神经网络，同时在其中也应用到了受控旋转门［12～14］。同样，量子神经网络在实际应用中也用途广泛，比如频谱感知［15］、音频水印［16］、网络攻击同源性判定［17］等方面。国内外众多学者不断在量子神经网络领域努力探索和研究，提出很多新的模型和理论，充分表现出量子神经网络在未来科学发展领域中的潜力。

深层、超深层储层处于盆地构造环境的下方，经过了长期的埋藏和压实、溶蚀等作用而形成［18］。深层、超深层有利储层识别的难点主要有两个方面。一是有利储层的识别过程中对特殊储层的形成机理认识不够充分、评价存在过度经验化的问题，二是对真实地质参数进行采集也是一个工程难点。针对深层、超深层储层识别问题，本文给出了基于量子神经计算的全新解决方案，应用结果表明，该方案在识别效率、泛化能力等方面相比于普通BP网络有较大优势。

2 量子神经网络模型

2.1 量子比特

量子在经典数字计算机中，信息被编码为信息位，单位是比特。不同于经典计算模式，在量子计算中，用0和1表示微观量子的基本状态，他们也是单量子比特的基态，单量子比特的任意状态都可以表示为这两个基态的线性组合。比特和量子比特的区别在于，量子比特的状态还可以是基态的线性组合，通常称其为叠加态。例如：

其中α、β是一对复数，称为量子态的概率幅，且满足 |α|2+|β|2=1，即量子态 ϕ 因测量导致或者以|α|2的概率坍缩（Collapsing）到0 ，或者以 |β|2的概率坍缩到1。量子比特也可借助三角函数表示为

其中φ表示量子比特 ϕ的相位。上式也通常表示为向量形式 ϕ =[cosφ sinφ]T。

2.2 通用量子门

在量子计算中，量子门可以对量子位的状态进行一系列的酉变换，发挥逻辑门的作用，实现逻辑变换的效果，因此，量子门也被定义为一种在一定时间间隔内可以对量子实现逻辑变换的装置。作为量子计算的物理实现基础，量子门在量子计算中占有重要地位。已经证明，量子门中存在通用量子门组与经典比特中与非门的通用性类似，由它们可以组成任意的量子门，一位相移门和两位受控非门可以组成最基本的通用量子门。

一位相移门定义为

2.3 量子神经元模型

本文提出了基于通用量子门的量子神经元模型，它的结构如图1所示，包括有输入、移相、聚合、翻转和输出五部分。其中，输入部分如图中的xi，用量子位表示；输出为量子位处于1状态的概率幅；移相和翻转操作分别由量子相移门R(θi)和受控非门U(γ)来实现。

图1 量子神经元模型

在图1中，式（4）定义了模型中的量子相移门R(θi)，对受控非门U(γ)定义如下：

其中 f是Sigmoid函数，C(·)的定义即式（4），输入部分xi先经过R(θi)移相，在通过图1中的求和符号实现聚合运算，定义如下：

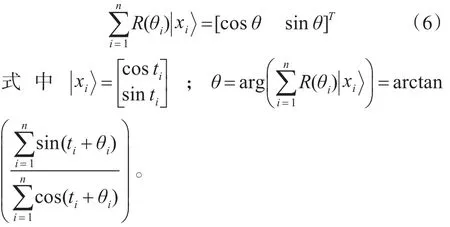
上式中的聚合结果经受控非门U(γ)作用，完成翻转操作，其结果如下：

量子神经元的输出值是经过翻转操作的量子位处于1状态的概率幅，也就是式（7）中的因此，量子神经元的输入输出关系为

2.4 量子BP网络模型

量子BP网络是按照BP网络的拓扑结构和连接规则由若干个量子神经元、传统神经元组成的，本文提出的三层前馈QBP模型拓扑结构如图2所示。其中，输入层有n个量子神经元，隐含层有p个量子神经元，输出层有m个传统神经元。各层神经元之间采用全连接。学习算法采用BP算法，利用量子计算特性可有效提升网络逼近能力。

图2 量子BP网络模型拓扑结构

该网络输入为xi，隐层的输出为hj，网络的输出为 yk，R(θij)是对隐层量子神经元进行更新的量子旋转门，wjk是隐层、输出层之间的连接权，可以将受控非门C(0)和U(αj)看做是从输入层到隐层的传递函数。各层之间的出入和输出关系描述为

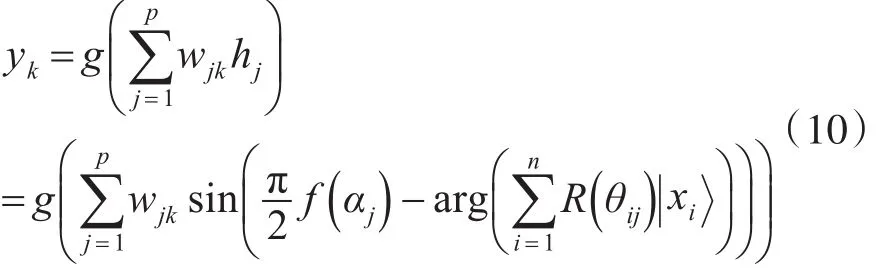
其中，i=1，…，n；j=1，…，p；k=1，…，m。

2.5 量子BP神经网络学习算法

2.5.1 训练样本的量子态描述

将量子神经网络应用于实际问题时，需要先将待训练的实值样本转换为量子态描述。设n维欧式空间下训练样本的实值向量为Xˉ =(xˉ1，xˉ2，…，xˉn)T，量子态转换公式定义如下：

2.5.2 网络参数更新规则

在量子BP网络模型拓扑结构中，共需要调整三组参数：θij—旋转参数，αj—翻转参数；wjk—连接权值。网络模型的误差函数定义为

3 基于QBP的超深层储层识别方案

为了验证本文提出QBP网络模型的先进性，本节将QBP网络与普通BP神经网络、基于正交基展开的过程神经网络（PNN）对比。

3.1 超深层储层识别指标集构造

建立和分析数据库会提高研究的效率。本节对收集的测井原始数据进行加工处理并建立数据库，对储层状况进行识别与分析，构造出评价指标集从而对深层、超深层储层识别展开研究，在样本数据库中建立数据和地下油层状况的对应关系是非常有必要的。

石油开发应用的基础之一就是油气储层识别，在我国的大部分油田中，一般采用对取芯井数据进行测试分析的方法进行研究，并结合实际采油数据进行综合分析处理，然后得到准确的储层识别分析结果，最后将实际结果和测试结果进行比较分析。

由于打芯井的造价很高，通过取芯井获取到的测井数据量相对较少。而且测井使用的技术方法多样，不同的测井方法所得的数据也会出现数据格式和结构之间不兼容的问题，所以在处理数据时需要对此加以注意。本文使用的取芯井测井数据源于同一油藏区块（徐深1、1-1、1-2、1-3、1-4共5口取芯井），地质构造相近、属性特征相似，并且具有相同的在测井技术和数据格式。

测井位点的间隔为0.125m，每个探测位点的所有属性集合作为一条记录进行保存，所有位点属性有效记录总量为14183。探测位点记录的维度包括：DEP（深度），LLD（深侧向电阻率），GR（自然伽马），CAL（井径），LLS（浅侧向电阻率），RHOB（补偿密度），CNL（补偿中子），DT（声波时差），POR（孔隙度）。

通过研究测井理论、分析现场数据资料并结合专家意见，最终选取LLD（深侧向电阻率），GR（自然伽马），LLS（浅侧向电阻率），RHOB（补偿密度），CNL（补偿中子），DT（声波时差）6个测井参数作为储层评价的指标集。

3.2 网络结构设计

根据网络结构设计原则，本文将徐深储层评价指标特征数据和储层类别数进行筛选，根据筛选后的数据来设置预测模型的结构。由于选做评价指标集的测井数据指标有6个，因此将QBP和普通BP网络输入节点设置成6个，PNN网络输入节点取1个，采用6个傅里叶基函数对输入实施离散傅里叶变换。各个模型的输出是6种储层类别，因此所有模型网络的输出节点都只有1个。为了提升模型的训练效率，同时保证网络优化能力，经多次实验，最终确定将网络结构中隐层节点数量设置为10个。

3.3 评价模型参数设计

储层地质类别划分为6个，因此网络的输出为6 级，每级宽度是 1∕6，整体划分作 0，1∕6，…，5∕6，1。所以，网络输出的精确度设置为1∕12。在QBP网络中，随机地选择之间数值赋给隐层旋转角度，随机选择（-1，1）之间数值赋给网络翻转参数，随机选择（-1，1）之间数值赋给输出层的权值。PNN和普通BP的参数在区间（-1，1）取随机值，学习速率设置为0.8，限定迭代步数取3000步。

3.4 储层识别方案设计

由于每个储层类别的储层厚度不同，各个储层数据样本集合的数据量存在很大的差别。但为了使网络训练样本更具有全局代表性，我们将上述的14183条数据全部用到网络学习预测中。而对于每一口井，取其数据量的90%作为训练集，剩余10%作为测试集，其中：

徐深1井训练样本3488条、测试样本387条；徐深1-1井训练样本2448条、测试样本272条；徐深1-2井训练样本3049条、测试样本339条；徐深1-3井训练样本2098条、测试样本233条；徐深1-4井训练样本1682条、测试样本187条；所有井用于训练的样本总数为12765条，测试样本1418条。

为了增强实验对比结果的可靠性，在训练样本、测试样本完全相同的情况下，对以上三种网络模型分别训练测试30次，将30次实验结果的平均值作为网络训练结果优劣的评价指标。

储层识别方案设计如图3所示。

图3 储层识别方案设计

4 超深层储层识别结果及分析

4.1 储层实测数据

在储层类别划分中通常包含有以下几个类别：油层、低产油层、油水同层、含油水层、可能油层；气层、低产气层、气水同层、含气水层、可能气层；水淹层、水层、干层。对松辽盆地徐深气田测井数据进行储层分层后得到了118个分层段。其中干层（储层级别为1）84个，差气层（储层级别为2）16个，气层（储层级别为3）10个，可疑气层（储层级别为4）1个，含水气层（储层级别为5）1个，裂隙油层（储层级别为6）6个。

以徐深1井为例，储层评价指标集实测数据如表1所示，其中，井号为徐深井区岩心井井号，井段储层类别中的1、2、3…，代表测量位点距离地面的深度，代表储层划分级别。LLD（浅侧向电阻率）、GR（自然伽马）、LLS（浅侧向电阻率）、RHOB（补偿密度）、CNL（补偿中子）、DT（声波时差）为储层评价指标集属性。

4.2 储层识别结果

用3种预测模型对样本数据分别学习和识别30次，QBP模型收敛数是29次，训练样本集中样本数目共有12765条，识别准确数的平均值为12332条，准确率的平均值等于96.61%；对于1418条测试样本识别准确数的平均值是1153条，准确率的平均值等于81.31%。

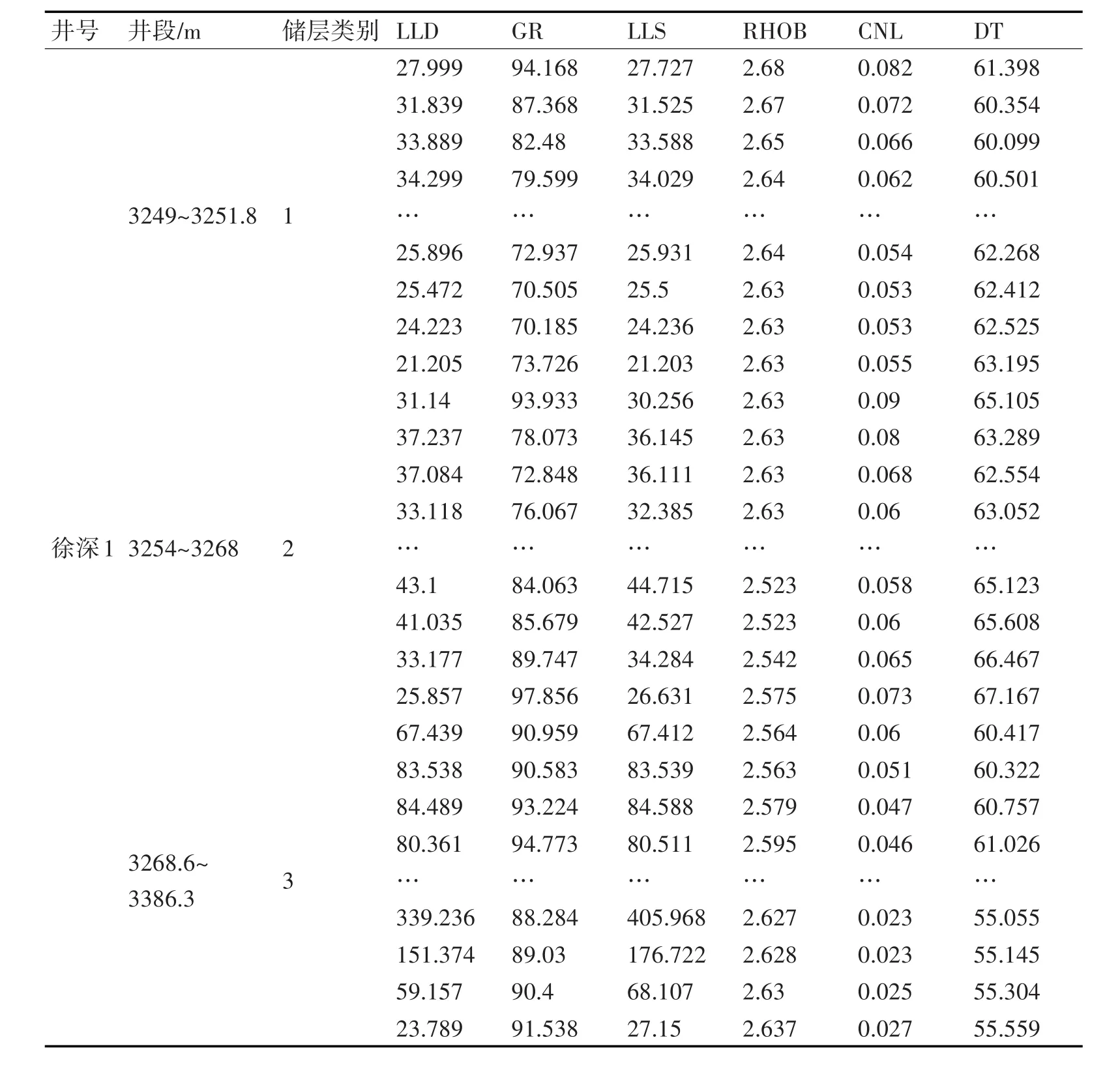
表1 测井位点分层数据

PNN预测模型的收敛次数是24，对于12765条训练样本集识别准确数的平均值是11466条，训练样本识别准确率的平均值等于89.82%；对于1418条测试样本集准确数的平均值是985条，准确率的平均值等于69.46%。

普通BP预测模型的收敛次数是20，对于12765条训练样本集的识别准确数的平均值是10601条，训练样本准确率的平均值等于83.05%；对1418条测试样本的识别准确数的平均值是925条，识别准确率的平均值等于65.23%。

三种评价模型训练结果见表2。

表2 QBP、PNN和BP网络30次训练结果数据统计表

预测结果表明，本文提出的QBP储层识别方法，对训练集的识别率非常高，正确率超过PNN模型6.79%，超过普通BP模型13.56%；观察测试样本的正确率可以发现，QBP同样表现出了较好性能，正确率超过PNN模型11.85%，超过普通BP模型达到了16.08%，真实反映了QBP用于识别徐深油气田储层识别所具有的评价优势。

4.3 识别结果分析

设计储层识别方案并对比识别结果发现，QBP预测模型相较于其他两种预测模型算法在多次重复训练过程中不仅具有领先的收敛次数，而且在对储层样本训练数据和测试数据识别准确率方面也占有较大优势。通过分析网络结构和模型训练算法，认为本文将QBP网络模型的分层中嵌入了基于量子计算机制而设计的量子神经元，提高了网络整体的非线性映射能力，同时提高了网络负载量，所以在储层评价指标集多维度、多数据量的训练过程中表现出结构设计上具有的理论优势。

5 结语

本文在分析测井数据源的基础上，设计了QBP网络模型的储层识别方案。首先，在综合储层评价理论与方法和分析测井数据的基础上，构建出了深层、超深层储层评价指标集；然后，根据量子神经网络的计算机制，对实际测井数据进行预处理操作，确定出网络模型的训练集和测试集数据样本；最后，通过实验证实了该方法对测井数据具有较高的学习能力和识别能力，也为解决油气田开发过程中的深层、超深层储层识别问题提供了一种较好的可行方案。