基于改进双适应度遗传算法的碎纸片拼接

张 岩，申 鹏，韩家宁，韩 超*

(1. 华北理工大学 化学工程学院，河北 唐山 063000；2. 哈尔滨商业大学 计算机与信息工程学院，黑龙江 哈尔滨 150000)

0 前言

文物修复、虚拟考古、司法物证鉴定等领域广泛存在着碎片拼接问题，大都可以近似归结为二维碎片的拼接问题[1]，将其抽象，可以近似看作轮廓曲线的匹配的一种特殊形式，而且目前大部分对碎片拼接复原方法的研究也主要集中轮廓曲线匹配上[2]，如，贾海燕等[3]人研究了碎纸片轮廓提取技术，通过碎纸片评分的大小来实现对碎纸片的拼接。朱延娟等[4]人提出基于 Hausdorffig 距离的多尺度轮廓匹配算法来解决碎片拼接问题。周丰等[5]人提出了基于角序列的与多尺度空间相结合的轮廓曲线匹配算法，也能很好的实现碎片的拼接问题。从理论上讲在物体拼接中，应用轮廓曲线的匹配关系，能够实现二维破碎物体的拼接[6-8]，其原理就是对边缘特征的识别与匹配[9]，但由于碎纸机的发明，碎片边缘正整齐，很难通过边缘识别技术对文件进行修复，所以形状在碎纸机粉碎的碎纸片的拼接中不能发挥作用。因此许多学者针对文档特征提取了不同的文本特征来进行拼接，王玉霞等[10]人根据碎纸片的左右边缘像素的相关性来实现碎纸片的拼接，罗智中等[9]人则利用多数文档的文字行方向和表格线方向平行且单一的特征来进行拼接，但由于采用的特征单一，匹配规则单一，匹配精度较低，人工干预几率大，而且单页文档经碎纸机破碎后其碎片都是成百上千个，计算量大、人工干预次数多且极易产生错误的匹配[11]，为此有必要进一步选择匹配特征和优化匹配原则。由于碎纸片大多来自同一页印刷文字文件被横切纵切为若干数量，形状均为相同的矩形，且两个碎纸片对象边界之间的破碎字符具有一定的相似性[12]。为此引入图像的灰度矩阵，灰度矩阵的每个元素对应到图像上的每个像素点，每个碎片均可以确定一个同型的灰度矩阵，灰度矩阵的特征反映了图像的特征。用matlab 的imread 函数读取图片的灰度信息，颜色越深，灰度值越大。为保证灰度匹配模型中绝对值的和不受这个约束的影响，同时简便计算，需将灰度值矩阵进行转化为0-1 矩阵，若灰度值矩阵中某个元素灰度值小于255，则0-1 矩阵中相同位置的元素值记为0，否则记为1。

1 碎纸片特征

1.1 碎纸片行高

由于英文按照四线三格的书写规则书写，因此行高可分占中间一格、上中两格和中下两格三类，如图1 所示。

图1 碎纸片的英文字母行高特征 Fig.1 The character of the letter height of a scrap of paper in English

经过对英文碎片和英文文档统计发现，只有每句开头和人名地名等是大写，其余均为小写，而在小写字母中，中间一格的使用率远远高于上下两格的使用率，故行高定义为中间一格竖直方向像素点之和，不同字母占格与使用率情况如表1 所示。由于中间一格的每行黑色像素点之和要远大于上下两格中每行黑色像素点之和，故可通过碎纸片上每行黑色像素点之和定位四线三格的位置。

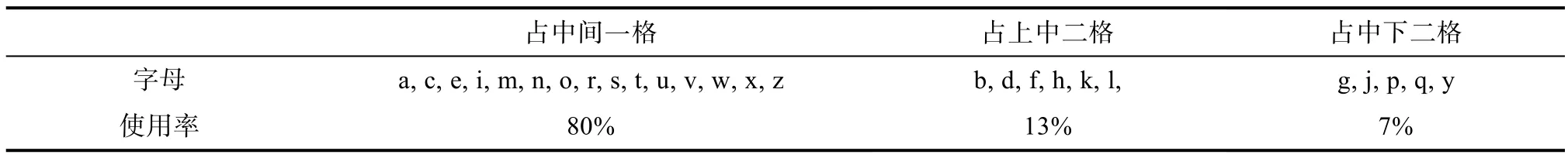
表1 不同字母占格与使用率 Table 1 The occupancy and usage of different letters

观察统计碎纸片上文字的字体及大小，找到某一临界值x（一行黑色像素点的和），假设碎纸片共有m行像素点，每行黑色像素点之和为，若，则i，j 为上中下三格的分界线，为行高。

1.2 行间留白

碎纸片确定行高之后，行与行之间的空白即为行间留白，行间留白高度为竖直方向像素点之和。

1.3 两侧留白

由于文档的书写规则，都会留有页边距，而文档的内部相对紧凑，故可通过左右两个方向的留白找出文档的最左和最右两侧的碎纸片，且相同一侧的留白大小应该相同。

2 碎纸片行间距类

将行及行间留白向右侧投影，如图2 所示，若遇到空白行超过行间留白高度时应按相应规则将其填补，如图3 所示。

本来介于碎纸片最上端和最下端之间的行高或行间留白的高度是固定的，但由于一些碎纸片的上下两格中的某些行黑色像素点之和大于临界值x，导致部分介于碎纸片最上端和最下端之间的行高或行间留白的高度有偏差，为解决这个问题，可先确定行高p 和行间留白高度q，并在每一个碎纸片中找到符合的最优行高(或最优行间留白高度)，以此为据向上和向下的q个像素点为行间留白（或p个像素点为行高），以次划分行和行间留白的位置。

图2 文字行及行间留白的右侧投影 Fig.2 Right side projection of text line and space between lines

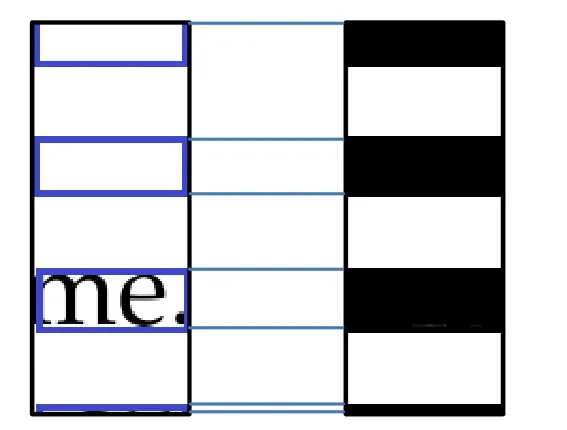
图3 规则填补 Fig.3 Replenish regularly

由投影可得出碎纸片的特征行向量，通过对特征行向量的相关性分析，可将碎纸片分成n 类，每一类即为文档的一大行。

3 边缘匹配度

3.1 分段最优边缘匹配度的计算

基于最小距离的边缘匹配度：

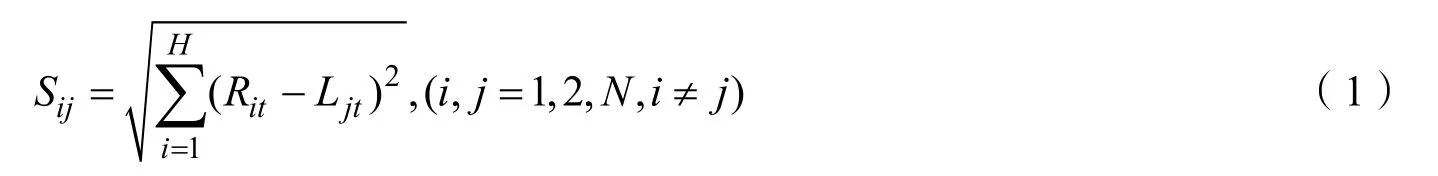
（1）由于文档的书写习惯，每段的最后一行通常会出现一部分空白行，若恰巧在此处被切割开，很难匹配到一起；

（2）由于两个字母（单词）之间有空白，恰巧挨着一个字母的结尾或另一个字母的开始切开，一侧有黑色像素点，一侧没有，也很难匹配到一起；

（3）由于某些文字的书写特征，如h,两竖和一横相连，若在相连的结点切开，也很难匹配在一起，如图4，此类英文字母还b，d，f，h，k，l，m，n，p，q，t，w，B，D，E，F，G，H，J，K，M，N，P，R，T，W，Y 等。

为此我们把基于最小距离的边缘匹配度进行优化，由于每类的行间留白的位置相同，故将每类中的碎纸片从行间留白的中线处切开，分成m 段，在计算匹配度时，分别计算两个碎纸片的每一段的边缘匹配度。并取其中最优值作为两个碎纸片的分段最优边缘匹配度。

第ij 碎纸片的第k 段边缘匹配度：

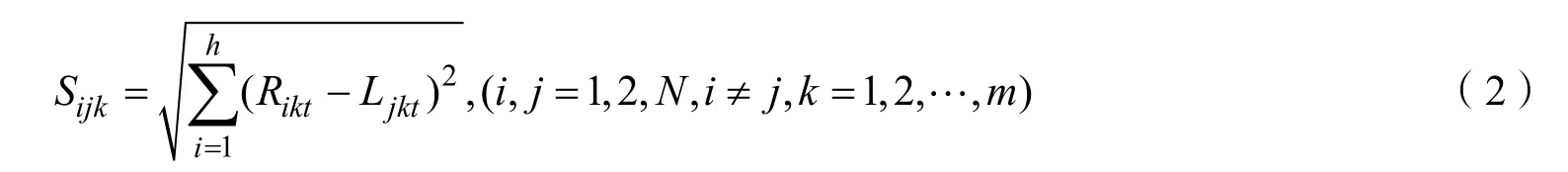
但应注意，若进行匹配的两个边缘皆为空白，应剔除，不并入计算。

3.2 分段空白列宽匹配度计算

在计算边缘匹配度时发现出两侧留白外，经常有左或右边缘没有黑色像素点的情况，如图5 所示。

图4 匹配效果 Fig.4 The matching effect

图5 段落左侧或右侧边缘无黑色像素点情况 Fig.5 No black pixels on the left or right edge of the paragraph

此时边缘匹配度为0，但出现匹配错误，为解决此类问题引入分段空白列宽匹配度，即两个单词之间的空白像素点之和Vk 是固定的，以此来推断空白列的匹配问题。同样将每类中的碎纸片从行间留白的中线处切开，分成m 段，分别计算两个碎纸片的每一段的空白列宽匹配度，并取最差值作为两个碎纸片的分段空白列宽匹配度。

则ij 碎纸片第k 段空白列宽匹配度：

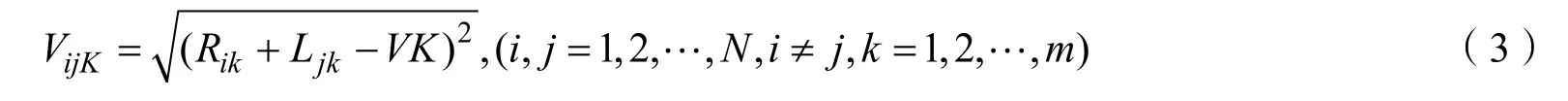
4 基于双适应度遗传算法的碎纸片拼接复原模型的建立

本模型采用双适应度遗传算法来解决多目标优化，其中拼接方案的两个适应度Fs和Fv分别依据分段最优边缘匹配度和分段空白列宽匹配度设计，具体流程如下图6。

初始种群p0的生成：根据分段最优边缘匹配度生成初始种群p0，大小为50。

交叉：将父代与适应度函数值相近的父代进行配对，再采用单点交叉，交叉率为1。

变异：本模型采用的变异率为0.05，随机地取两个在0到17之间的整数，对这两个数对应位置的基因进行变异，得到新的染色体。

具体计算步骤如下：

Step1：计算行高和行间留白；

Step2：通过规则填补后的投影进行字符定位及碎纸片的聚类；

Step3：计算分段最优边缘匹配度和分段空白列宽匹配度；

Step4：找出两侧留白，确定每一大行的开头结尾；

Step5：将所有类按碎纸片数量进行排序，根据分段最优边缘匹配度和分段空白列宽匹配度调用双适应度遗传算法并由从多到少的顺序对每类进行拼接，多余的碎纸片并入下一类；

Step6：每类拼接完后，进行横向拼接，方法同上。

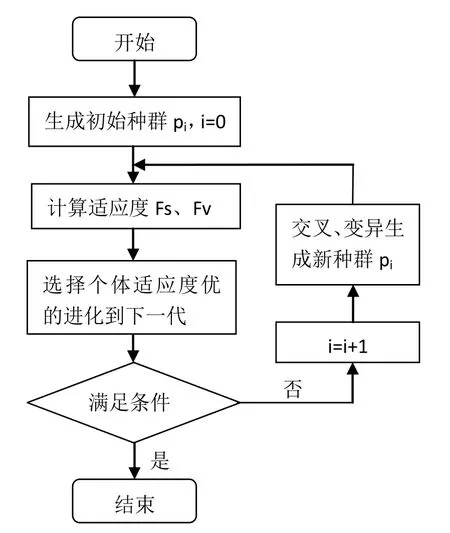
图6 双适应度遗传算法流程图 Fig.6 Flow chart of dual fitness genetic algorithm

5 实验过程

（1）计算行高和行间留白，通过规则填补后的投影进行字符定位及碎纸片的聚类，共分12 类，其中19 个碎纸片占10 组，18 个占1 组，1 个占1 组。

（2）找出两侧留白，确定每一大行的开头结尾，开头碎纸片编号为19，20，70，81，86，132，159，171，191，201，208，结尾碎纸片编号为31，44，82，109，112，115，127，143，146，147，178。

（3）将只含1 个碎纸片的那类并入碎纸片少的一类，调用双适应度遗传算法对每类碎纸片进行拼接，人工干预后，进行横向拼接，结果如表2 所示。

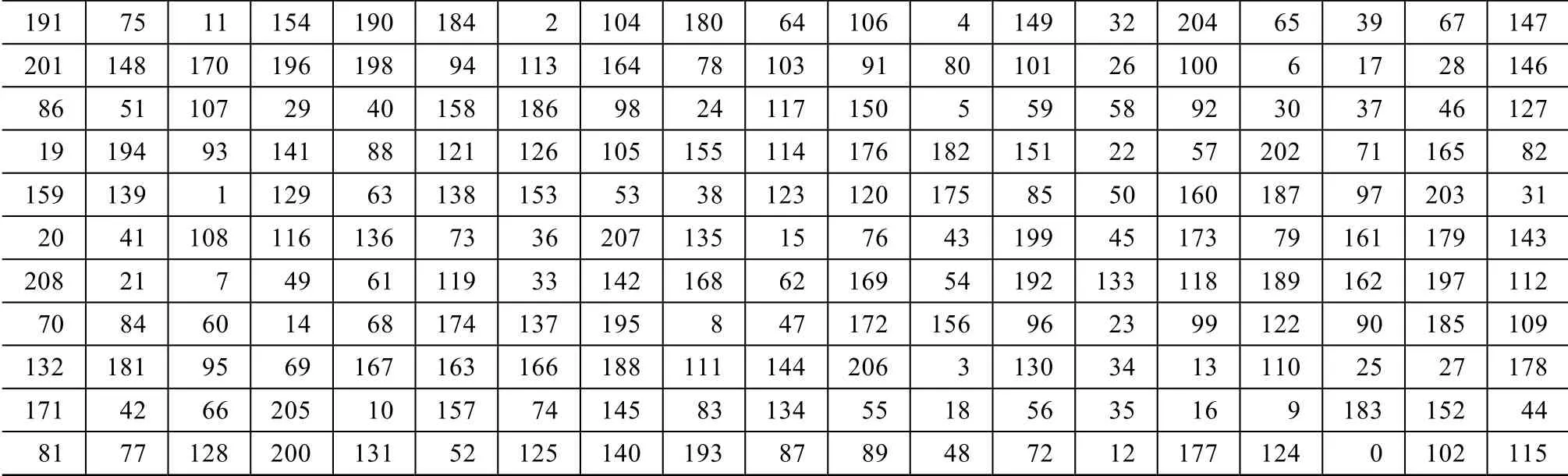
表2 拼接结果 Table 2 Stitching result

在进行人工干预之前，共有4 个碎纸片拼接错误，准确率达到98.1%，人工干预后准确率达到100%。其中拼接错误主要出现在一个碎纸片上文字信息过少或者一行中四线三格的上下两格使用率过高，导致字符定位不准确，为后续拼接带来了麻烦。

也应注意，在碎片拼接后，需要字符识别技术的支持，通过光学字符识别模型，将碎片拼接图像中的文字处理成可编辑的文本格式[12]，才能进一步提高碎片拼接的高效性。

6 结论

（1）通过对英文碎纸片的行高、行间和两侧留白分析，得到了对碎纸片字母利用率和占格分布情况统计的一般方法；

（2）通过设计规则填补而进一步定位字符位置，并通过最有行高（最优行间留白）优化字符位置，使得准确率达到了98%；

（3）设计并优化了分段最优边缘匹配度，避免了由于切割线两侧部分位置匹配度过低而导致的整体匹配度下降问题；

（4）设计了分段空白列宽匹配度，解决了由于进行边缘匹配计算的两个碎片边缘皆为空白而引起的分段最优边缘匹配度失灵的问题，建立了基于双适应度遗传算法的碎纸片拼接模型，得到了一般规则碎片的拼接方法；

（5）基于本文的研究，碎纸机可进行升级优化，以避免碎纸片拼接带来的不良影响，可变换切割矩形的大小，也可尽可能多的从空白处切开等。