IPM电机反电动势设计对系统性能影响的分析

童 童，陈 彬，胡余生，卢素华

(1．空调设备及系统运行节能国家重点实验室，珠海519000;2．珠海格力节能环保制冷技术研究中心有限公司，珠海519000)

0 引 言

内置式永磁电机(以下简称IPM电机)具有装配工艺简单、结构强度高、可靠性好的优点，目前很多表贴式永磁电机(以下简称SPM电机)的结构都逐渐向IPM结构进行切换［1］。从数学模型上看:SPM电机的d轴和q轴电感值相近，且通常数值较小，一般采用id=0控制。IPM电机的d轴和q轴电感不相同，且q轴电感通常较大［2］，通常采用弱磁控制，以获得更大的合成转矩。

在电机理论计算及仿真中，电机的激励都采用理想正弦波电流［3］，通过数学模型可得出反电动势大小对于电机性能不造成任何影响的结论。鲜有基于PWM驱动、进行每个载波周期内电流分析的案例。反电动势的设计并未引起足够重视。

本文首先从高反电动势电机(以下简称高反电机)和低反电动势电机(以下简称低反电机)的电流波“毛刺”大的问题思考，从每个载波周期内的现象分析解释了该实验现象，且得出了过低的反电动势使得磁势谐波增加，引起铁耗增加的结论。然后进行实验数据分析，发现过高的反电动势使得母线电压饱和，弱磁控制引起的驱动电流增加。最后，结合设计经验，给出了如何统一过低和过高反电动势引起的矛盾问题，总结了针对系统效率最大化的反电动势设计原则。

1 理想波形下反电动势对系统性能影响分析

在理想正弦波电流条件下，建立IPM电机的数学模型，IPM电机d轴和q轴电感不相同，其转矩式如下:

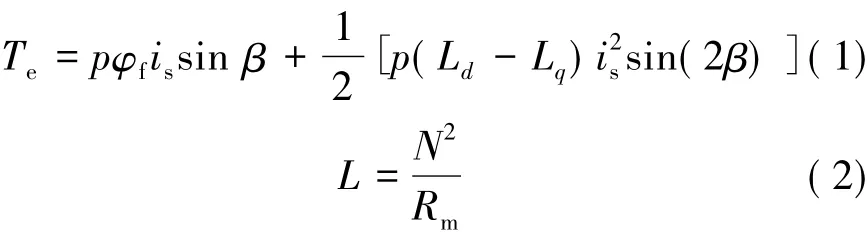
式中:p为转子极对数;φf为空载磁链;is为合成电流值;β为弱磁角;Ld，Lq分别为该电流下的直、交轴电感;N为绕组匝数;Rm为磁力线所经路线的磁阻。

由式(1)和式(2)可得:

电机损耗可以按照下式计算［4］:

式中:i为定子相电流;r为定子相电阻。

当槽面积和槽满率一定时，不考虑漆膜的影响，则有:

关于铜耗，式(3)和式(6)分别代入式(4)得出结论:在相同槽满率以及槽面积的情况下，同一定子铁心的电机，无论如何改变其匝数(反电动势)，相同的转矩输出下，其铜耗是不变的。

当导磁材料位于交变磁场中被反复磁化，此时B－H曲线在四象限所围成的关系便是磁滞回线，此时导磁材料中将引起能量损耗，称为铁心损耗。铁心损耗分为两部分:磁滞损耗和涡流损耗［4］。

工程上，常用ph表示磁滞损耗:

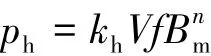
式中:kh为导磁体材料决定的磁滞损耗系数;f为磁场交变频率;Bm为磁化过程中的最大磁通密度，n通常取 1．5～2．0。

在IPM电机中，将其进行d，q轴模型等效后，涡流效应下，铁耗的等效表达式［5］:

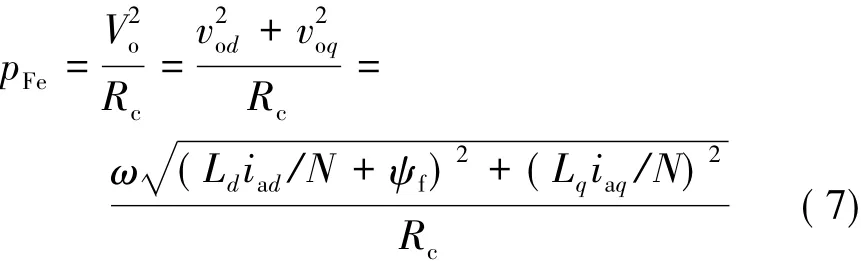
式中:Rc为所取环流的铁心等效电阻;ψf为永磁体产生的磁链;iad，iaq为涡流电流 d，q 轴分量;vod，voq为涡流电压d，q轴分量;Vo为涡流环路电压。

通过以上数学模型分析，反电动势对于电机损耗是没有影响的，而在实际PWM驱动下，该结论需要进一步讨论。

2 PWM波驱动下不同反电动势电机波形分析

如图1所示为基于PWM调试的电压波形。PWM波存在占空比，因此电流不可能是光滑、连续的，以上基于平滑的正弦波分析得出的结论需重新分析。

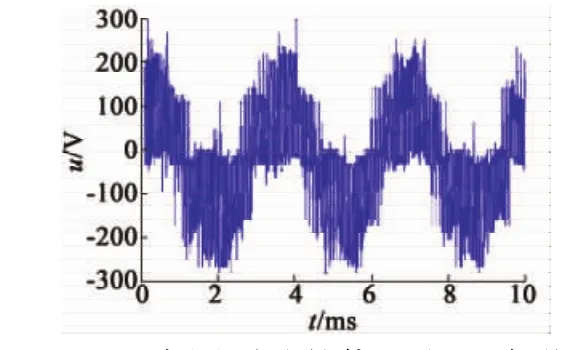
图1 实际测试的绕组电压波形

＇假设某驱动载波频率为fc，高反电机和低反电机绕组匝数分别为N1和N2，且N1/N2=κ。根据式(1)可得出:在同负载下，电流有效值I1/I2=1/κ;故U1/U2=κ，具体到每个载波周期内，高反电机PWM波的占空比α1同低反电机PWM波占空比α2存在以下关系:α1=κα2。

电感所形成的反电动势分为旋转反电动势和变压器电势，即:

IPM电机在一个载波周期内的旋转角度内，电感变化不明显，旋转反电动势很小，主要为变压器电势，式(8)可以简化:

取每个载波周期内波形分析，如图2和图3所示，由于L∝N2，结合式(9)得出，受电感差异的影响，高反电机和低反电机的电流上升斜率k1/k2=1/κ2不同［6］，故磁势变化斜率(N1k1)/(N2k2)=1/κ。下降过程亦然，有效值相当的情况下，斜率变化越大，对应分解后谐波的频率越高，从而导致铁耗增加［7］。低反电机的电流波形在宏观上显示为电流毛刺增加。

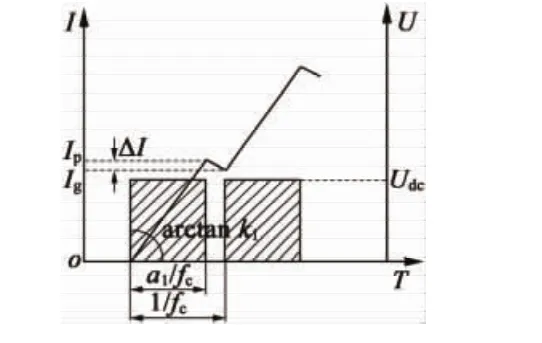
图2 高反电机每个载波周期电流、电压示意图

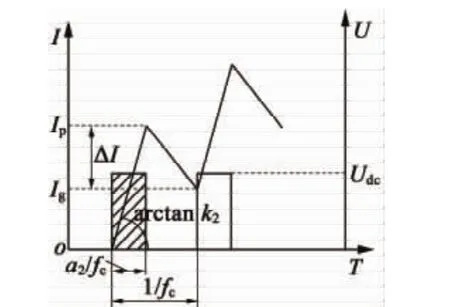
图3 低反电机每个载波周期电流、电压示意图

3 不同反电动势样机对比测试论证

以一款2．5 kW的IPM电机(p=3)为研究对象，高、低反电动势两种方案同期测试，分析电流谐波、铁耗以及系统效率的差异，为有效突出反电动势对电机和系统效率的影响程度，对比方案如下。

高反电机:58匝，低反电机:27匝。控制器载波:2．5 kHz，额定转速:3 600 r/min，额定负载:6．5 N·m。电流波形对比如图4、图5所示。

从电流波形上看，低反电机电流有效值接近高反电机电流有效值的2倍，符合式(3)。低反电机电流波形的“毛刺”明显大于高反电机。进一步的FFT分解，其27、29高倍频的谐波幅值相对较高，且产生了同载波频率相同的41倍频(2．5 kHz)。

图4 高反电机电流波形及FFT分析

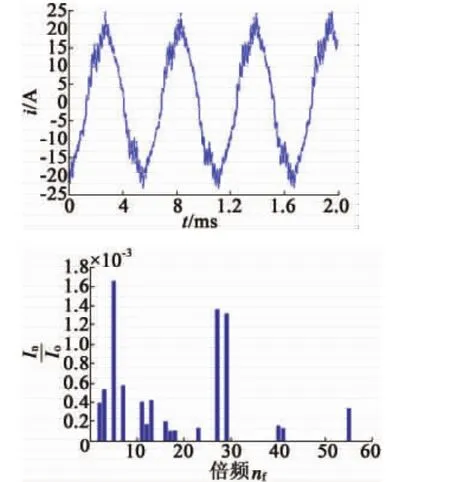
图5 低反电机电流波形及FFT分析

进一步的损耗对比如图6～图9所示。

从铜耗上看，低反电机略大于高反电机。主要是由于低反电机磁势(N2k2)变化较快，载波周期内控制不及时引起的超调导致，可认为是基本相当的。

图6 铜耗对比

从铁耗上看，低反电机明显大于高反电机。同前述分析一致，由于高频谐波导致涡流损耗的增加。

图7 铁耗对比

控制器的逆变模块同绕组在电路上看是串联的，低反电机运行电流大于高反电机，逆变模块的通态损耗增加，导致控制器损耗增加;随着负载的增加，二者损耗差异越来越大。

铁耗和控制器损耗的综合作用使得高、低反电机的系统效率差异明显。从实测曲线看，基于相同冲片结构的高反电机和低反电机的系统效率差达到4%。在实际设计中，虽然设计值不会距离最优目标值差一倍，但通过该实验足以看出反电动势设计对系统效率最大化的重要性。

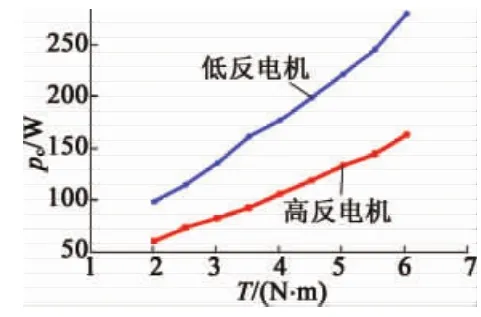
图8 控制器损耗对比

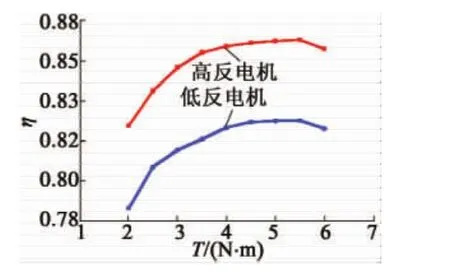
图9 系统效率对比

4 基于反电动势系统效率最大化设计总结

以上分析明确了高反电机的优势，但过高的反电动势也会导致系统效率下降。原因如下:控制器所采用的交－直－交的变频方式中，直流母线电压存在一个极限值，对于单相功率板，电压利用系数按0．95计算，开PFC(功率因数校正)情况下，最大输出电压有效值可达到240 V左右。电压饱和后，转速或负载继续增加，需要进行弱磁控制，控制器需增加额外弱磁电流，二次侧模块损耗以及电机铜耗均有增加。

表1和表2为上述实验对比样机在高速(4 800 r/min)时测试数据。可以发现，低反电机电压未发生饱和，线电压随输出转矩增加而逐步增加;高反电机在4 N·m时电压已经开始饱和，输出继续增加时，安匝明显大于低反电机。从效率上看，甚至出现了高反电机低于低反电机的情况。此时，若进一步考虑控制器二次侧模块损耗，系统效率加剧下降。

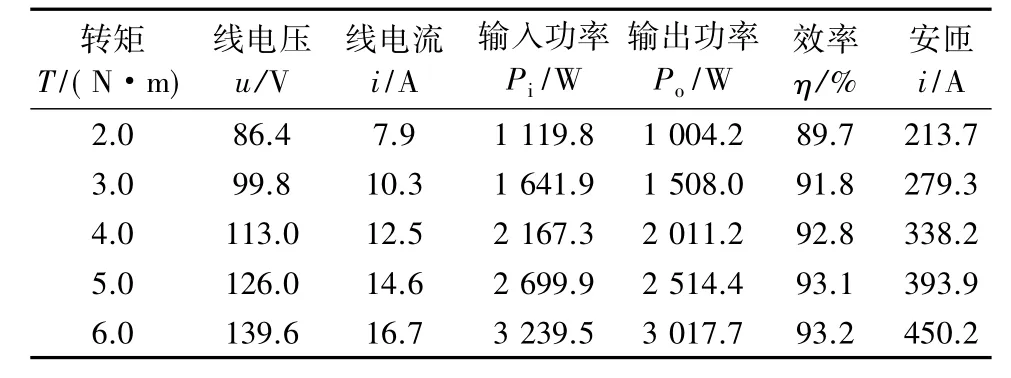
表1 低反电机4 800 r/min测试数据

表2 高反电机4 800 r/min测试数据

反电动势对电机性能影响总结如表3所示。

表3中的三个因素界定了最佳系统效率下反电动势范围:

(a)基于原方案提高绕组反电动势，最大工况下，绕组电流值i不得大于模块保护电流Imax，否则电机工作区间不达标。

(b)在增加反电动势、提升系统效率的过程中，避免效率下降，应当满足以下:Δi2(r+Rc2)＜－ΔpFe。其中Δi2为绕组提升过程中，弱磁电流增加部分，Rc2为控制器模块二次侧等效电阻。可以通过IGBT功耗仿真软件得出。ΔpFe为反电动势增加对于铁耗抑制的变化量。

表3 反电动势高低对电机损耗影响

假设电机在额定转速下以最大负载运行时电压刚好达到饱和，以此时的反电动势e0、铁耗值pFe0、绕组安匝Ni0为基准。通过多个不同反电动势样机的测试，不同反电动势标幺值下铁耗标幺、绕组安匝标幺的情况，如图10所示。可以参照图10选取合适的标幺值。

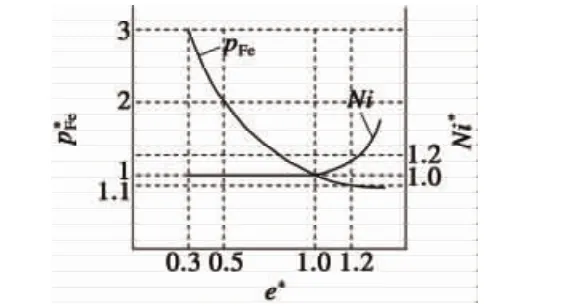
图10 不同反电动势标幺值下铁耗和安匝曲线

通常电机选型时需要关注以下几点:常规运行区间、极限运行区间，对于需要综合能效较高的场合，将最大系统效率点设计在常规运行区间附近，满足极限运行区间的能力，标幺值可取 1．0～1．05;对于经常出现极限运行区间，可以将最大系统效率点设计在靠近极限运行区间附近，标幺值可取0．8～0．9。

5 结语

本文在IPM电机数学模型的基础上，从理论和实际的差别点着手分析，找出了低反电机驱动电流“毛刺”大的原因，并发现高反电机通过自身电感来抑制磁势变化斜率，通过降低谐波达到降低铁耗的内在机理。

从设计实验、测试数据、损耗分析几个方面验证了分析结论。实验效果明显，两款样机的系统效率差值达到了4%，说明了反电动势的设计对于电机性能影响的程度。通过优化反电动势来提升系统效率也是一种最为经济的方式。然而IPM电机的驱动受到母线极限电压的限制，过高的反电动势也会由于弱磁角度变化引起性能下降。

为解决以上矛盾，总结分析了反电动势对电机的设计影响，给出反电动势设计的选取原则和考量因素。有助于电机设计者在根据不同的使用条件合理选择反电动势的大小。