决策曲线分析在R语言中的实现

中南大学湘雅公共卫生学院流行病与卫生统计系(410078)

陈乐陶 杨土保 陈 橙 张静航 贺志敏 郑 赞 秦家碧△

受试者工作特征曲线(receiver operator characteristic curve,ROC曲线)作为一种临床预测模型,被广大医学研究工作者使用。ROC曲线利用真阳性率和假阴性率作图,得到灵敏度和特异度的关系,确定诊断试验的最佳临界值,并通过曲线下面积(area under curve,AUC)比较不同模型的优劣。但ROC曲线唯一关注的就是预测模型的准确性,并不能在实际临床模型效用判断中提供帮助[1]。而决策曲线分析(decision curve analysis,DCA)恰好弥补了这一缺陷。DCA是一种能体现临床结局变量并可用于评估和比较不同预测模型的方法，受到越来越多来自医学研究工作者的重视。近些年,在医学外文期刊例如Lancet、JAMA、J ClinOncl等中陆续有文章采纳、介绍并推荐DCA的应用[2-4]。

方法与原理

1.背景介绍

DCA最早由Andrew J.Vickers和Elena B.Elkin在2006年介绍并发表于Medical Decision Making杂志上[1]。作者以一项预测前列腺癌患者是否应该接受全精囊切除手术的研究展开对DCA的阐述。前列腺癌的治疗手术在切除前列腺的同时往往还要切除全部精囊,以防止癌细胞扩散到精囊发生精囊浸润(seminal vesicle invasion,SVI)。SVI只有在切除手术后才能被检测,而对于那些实际并没有SVI的患者来说,将承受尿失禁或阳痿等较严重的副作用。所以有研究者建议对于SVI预测发生率高的患者直接采取精囊全切手术,而对于预测发生率低的患者采取精囊尖端保留的手术治疗。保留精囊尖端能避免切除重要的神经和血管,可减少副作用的发生风险,同样也会增加癌症复发的可能性。如何选择手术方法成了外科医生和患者共同面临的问题。之前的研究者普遍采用ROC预测,但并不能判别该模型结局的实际临床效益。所以Vickers引进了DCA这种方法,在不同的SVI发生率下,权衡患者可能得到或损失的临床效益(如健康、经济、精神等方面),通过比较净获益(net benefit,NB)值的大小预测实施哪种手术方法。至今为止,DCA已经被广泛应用在癌症研究且逐渐扩展到其他研究领域中[4]。

2.应用领域

DCA方法实质上是根据不同影响因素构建的模型来预测临床结局。通过预测不良事件发生的概率制定干预措施,从而改善患者健康、提高个性化治疗的应用,促进公共卫生领域的发展[5]。目前DCA方法主要应用于预测诊断试验结局、术后结局及比较不同模型的优劣。例如预测前列腺癌患者存在SVI的概率[1](预测诊断结局),预测心脏手术后患者的死亡率[6](预测术后结局),选择评价房颤患者口服抗凝药出血风险的最优模型[2](比较不同模型优劣)。同时,为了完善和改进DCA方法,很多研究者就其方法学进行深入的研究与探索。

我们在Pubmed上以decision curve analysis为关键词限定在题目和摘要检索,共检索出259篇相关文献。从2006年到2016年有关DCA主题的发表文献数量及趋势见图1。这表明DCA模型已经受到了越来越多来自医学相关工作者的关注,并逐渐渗透、应用于实际临床科研中。

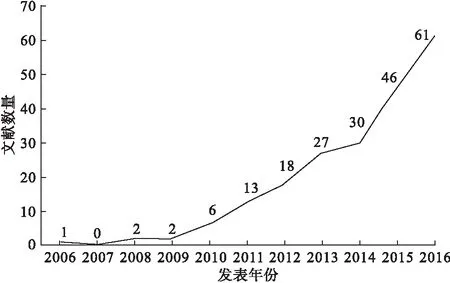
图1 在Pubmed上检索的不同发表年份下关于DCA的发表文献数量趋势图

3.DCA原理

DCA的产生基于一个原则[7],即假阳性(如不必要的活检)和假阴性(如漏诊癌症)的相对损失值可以用阈概率表示。假定患癌症的概率大于20%时应选择活检,那么当受试者患癌症的概率小于20%时,漏诊癌症产生的损失值是接受不必要活检损失值的四倍,这意味着阈概率的值决定了损失的相对比值。总之,阈概率的值既可以决定受试者的临床结局又可以使用临床净效益函数对真阳性和假阳性的临床结果建模:

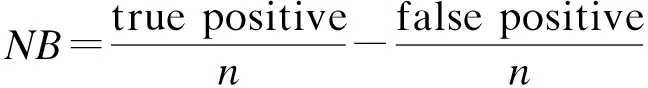
其中,n为样本量、Pt为阈概率、true positive、false positive分别为真阳性和假阳性患者的数量。NB就是根据这一理论平衡了收益值与损失值之间的关系。如果受试者的NB在可接受范围之内,就会被建议采取干预或相应治疗措施[4]。

DCA曲线的产生可以分解为以下步骤[7]:

(1)选择合适的阈概率Pt；

(2)受试者A发生不良结局的概率为a,当Pa>Pt时,为阳性；

(3)计算真阳性和假阳性的个数；

(4)计算净收益值；

(5)改变Pt值并重复上述步骤。

事实上,DCA曲线的产生就是通过一系列阈概率的变化从而改变NB的大小。

4.DCA与ROC的联系与区别

ROC和DCA都属于预测模型,都可以用来评价不同模型的优劣,但ROC和DCA在理论构建上有着本质区别[5]。

ROC结合了所有灵敏度与特异度，通过比较AUC决定预测模型的准确性。但在实际临床应用中,AUC值最大并不代表模型最优。就好比上文中提过的前列腺癌患者的全精囊切除手术,尽可能降低假阳性患者的数量是决策者需要考虑的问题,尽管此时的ROC未必最优。另一方面,对于极端情况,准确性已不那么重要。比如患病的概率小于0.2时可以不做任何干预或治疗措施,概率大于0.8时应采取措施,细小的概率差异显然不会影响医生的决断。而当概率在0.2～0.8之间时,是否采取措施才是医生和患者需要考虑的,此时显然要使用DCA这种预测模型。

DCA是用来预测临床结局变量的模型。DCA最适用的情况是，有症状预示可能患病但未被确诊时,是否采取及采取何种筛查方法来诊断疾病。由于筛查方法往往存在着不同的风险和副作用,受试者患病的概率、可能的副作用、患者的意愿及医生的经验都会影响最终的决定。很显然,在极端情况下如何抉择并不难,而在特定的区间概率范围内就依靠DCA提供决策评价。ROC与DCA具体的区别如表1所示。

表1 ROC与DCA区别

实例分析

为了更好地说明DCA方法的应用,我们以一项病例对照研究为例具体展示R语言的操作。该研究目的是探究不同影响因素与冠心病发生的关系。研究对象为湖南省长沙市居民,研究样本量为324,其中冠心病患者组156人,对照组168人,自变量分别为x1(年龄)、x2(高血压史)、x3(高血压家族史)、x4(吸烟)、x5(高血脂史)、x6(动物脂肪摄入)、x7(体重指数BMI)等,结局变量为Y(是否发生冠心病)。查阅文献资料得出中国城市居民的冠心病发病率约为1.3%[8]。

为比较不同变量构成方式对冠心病发生的预测,在此构建三种模型。模型single、triple、total分别代表纳入一种、三种及全部变量,即分别探讨单因素、部分研究因素、全部研究因素与冠心病发生的关系,通过DCA作图,直观观察并选择预测结局的最佳模型。

(1)安装程序辅助包

DCA的绘制无法直接在R软件中实现,需另下载专有的DCA相关R辅助软件包。

在R (3.4.1) 软件中直接输入以下程序,即可以下载完成绘制DCA所需的安装包。

library(devtools)

install_github(“mdbrown/NetBenefitCurve”)

或直接输入install.packages(“rmda”)

rmda:为risk model decision analysis的缩写,是绘制DCA所需的R辅助包

(2)读取数据

安装包下载安装成功后,直接在R软件中输入下列程序：

setwd("D:\DCA")

Data<-read.csv("coronary heart disease.csv",header=TRUE,sep=",")

library(rmda)

数据以D盘DCA文件夹下名为coronary heart disease的excel格式存储的

read.csv:读取excel格式的数据;library(rmda) 激活R辅助包。

(3)构建三种模型

single<-decision_curve(Y～x7,data = Data,family=binomial(link =′logit′),

thresholds= seq(0,1,by = 0.01),confidence.intervals =0.95,

study.design= ′case-control′,population.prevalence=0.13)

探讨单因素与结局变量的关系;在logistic回归基础上,以Y为因变量,x7为自变量构建模型。thresholds设定阈概率的范围为0～1,也可根据具体实际情况规定阈概率范围。该例研究为病例对照研究,人群发病率为1.3%。

需要说明的是,此套R程序同样适用队列研究,只需将代码’case-control’换为’cohort’,将population.prevalence= 语句删除,即可。

triple<-decision_curve(Y～x1+x2+x7,data = Data,

family = binomial(link =′logit′),thresholds= seq(0,1,by = 0.01),

confidence.intervals =0.95,study.design = ′case-control′,

population.prevalence = 0.13)

探讨部分研究因素与结局变量的关系。

total<-decision_curve(Y～x1+x2+x3+x4+x5+x6+x7,data = Data,

family = binomial(link =′logit′),thresholds = seq(0,1,by = 0.01),

confidence.intervals= 0.95,study.design = ′ case-control’,

population.prevalence= 0.13)

探讨全部研究因素与结局变量的关系。

4.绘制DCA

List<-list(single,triple,total)

将single、triple、total三条曲线并列在一张表格上

plot_decision_curve(List,curve.names= c(′single′,′triple′,′total′),

cost.benefit.axis =FALSE,col = c(′red′,′green′,′blue′),

confidence.intervals =FALSE,standardize = FALSE,

xlab="Threshold Probablity")

以Threshold Probablity为横轴,Net Benefit为纵轴,绘制DCA曲线图。如只需单条曲线预测模型,将代码List换为single或triple或total,在names和col保留想要的曲线名称和颜色即可。

图2 对三种不同模型进行比较的决策曲线分析图

决策曲线的解释依赖于预测曲线的净收益与两种极端情况曲线的净收益相比较。在特定的Pt中,拥有最高的净收益值的策略是最优的。图2是三种不同预测模型结局获益的比较。五条曲线分别代表:三种不同纳入因素的预测结局;所有受试者都不是冠心病患者(Pa

讨 论

ROC曲线、校正曲线及分类表等评价方法主要注重如何提高预测模型的准确性,对模型之后的临床结局关注甚少。但往往临床结局的预测结果会直接影响医生的决断,而一味地追求准确性可能会忽视患者真实的需求[9]。

DCA方法实质上是根据不同影响因素构建的模型来预测临床结局。通过预测不良事件发生的概率制定干预措施,从而改善患者健康、提高个性化治疗的应用,促进公共卫生领域的发展。作为一种评价诊断试验、预测模型和分子标记的新兴方法[7],DCA正逐步应用于医学研究中。如何准确绘制DCA曲线也成为当前需要解决的问题。到目前为止,并没有具体文献指导操作DCA的绘制方法。本研究以实例为证,阐述针对队列研究和病例对照研究,如何在R软件中实

现DCA曲线的绘制,方便医学研究工作者的使用,为推进DCA方法的应用与探索提供帮助。