基于排队论模型的《卫生统计学》课程中心建设优化研究*

四川大学华西公共卫生学院流行病与卫生统计系(610041)

张 韬 吴芸芸 刘元元 高 旸△

近年来,高校学生探索和创新意识逐渐增强,学习兴趣日益浓厚,提出的问题质量和数量都明显增多。由于班级人数多、课堂时间少,同学们的问题不能及时得到解答,而任课教师随堂为同学们答疑解惑的时间和精力有限,如何提高教师为学生答疑的效率进而满足学生的需求,成了亟待解决的问题。

为提高课后答疑效率,本授课团队(由一位任课教师和两位研究生助教组成)在2017年春季学期利用四川大学课程中心平台,鼓励学生将问题发布在课程中心的论坛模块,由授课团队对问题进行在线解答。在此基础上,本研究首次运用排队论模型对课程中心排队系统及应用效果进行研究,从而对授课团队的人员配备情况进行优化设计,并为课程中心的优化提供参考。

对象与方法

1.资料来源

本研究选取四川大学2017年春季学期《卫生统计学III》课程某班的149名同学为对象,调查其在课程期间(2017年3月12日至5月19日)对课程中心的使用情况及利用效率,具体包括发帖类型、发帖时间以及帖子被回复的时间。其中,课程中心的发帖类型包括“答疑解惑”、“学习收获”和“心得分享”三种,时间单位按天计。

2.研究方法

鉴于设计课程中心的目的是提供课后答疑解惑的在线平台,同时在这个平台上提出问题和等待解答的过程具有一定的随机性,因此可以通过将该平台上提出的问题看作“顾客”、将答疑者看作“服务窗口”或“服务机构”,从而把课程中心理解成一个随机排队系统。在此基础上,本研究将课程中心的建设优化的实际问题转化成为排队系统的参数求解与优化的数学理论问题。排队论是运筹学的重要分支学科,主要通过数理方法研究如何优化服务机构,使得服务机构既能满足顾客的需要,又能使服务机构自身最为精简[1]。目前排队论模型已广泛应用于交通、运输、银行、旅游和医疗等行业[2-6]。在本研究中,排队论模型的具体应用过程包括课程中心排队系统的建立、模型参数及其估计和课程中心排队系统的优化。

(1)课程中心排队系统的建立

排队系统主要由输入过程、排队规则和服务窗口三部分组成。其中,除了上述提到的服务窗口以外,输入过程刻画问题按怎样的规律到达课程中心,排队规则反映服务窗口(即答疑者)以怎样的方式提供答疑服务。以下是本研究对这三个部分的具体设置和规定。

①输入过程

在课程中心排队系统中,由于每个同学可能提问的个数是随机的,因此问题源是无限的。如果各个同学在课程中心提问的时间间隔相互独立,那么单位时间内课程中心的提问发帖数则服从泊松分布,设参数为λ,则课程中心两个提问发帖的时间间隔(即到达时间间隔)服从期望为1/λ的负指数分布。通过拟合优度卡方检验可判断课程中心排队系统的到达时间间隔是否服从负指数分布。

②排队规则

课程中心平台不限定系统容纳的最大发帖数,因此系统能够容纳的问题数是无限制的。在课程中心平台,答疑者通常遵循“先提问先解答”的规则。

③服务窗口

由于在实际的教学过程中,课程中心里提出的问题主要是由任课教师和研究生助教进行解答的,因此本次建模暂时不考虑学生之间相互答疑的情况,从而将课程中心排队系统的服务窗口个数设定为c,其中c是授课团队的人数。本门课程的授课团队共有一位任课教师和两位助教组成,因此c=3。在以上假定的前提下,进一步定义从答疑者开始思考提出的问题到该问题被答疑者回复的时间为服务时间。一般情况下,服务时间的分布是随机的,此时服务时间服从参数为1/μ的负指数分布。其中,μ是指每个答疑者平均每天能解答的问题数,1/μ为平均服务时间,即每个问题从开始思考到被解答的平均时间。通过拟合优度卡方检验可判断课程中心排队系统的服务时间是否服从负指数分布。

综合以上三部分的特征,系统可表示为M/M/c/∞(图1),即问题来源是无限的,问题进入系统的时间服从参数为λ的负指数分布,课程中心平台服务时间服从参数为μ的负指数分布,系统设置c个并联服务窗口,系统对排队的问题数没有限制。由此本研究得到课程中心随机服务系统模型。

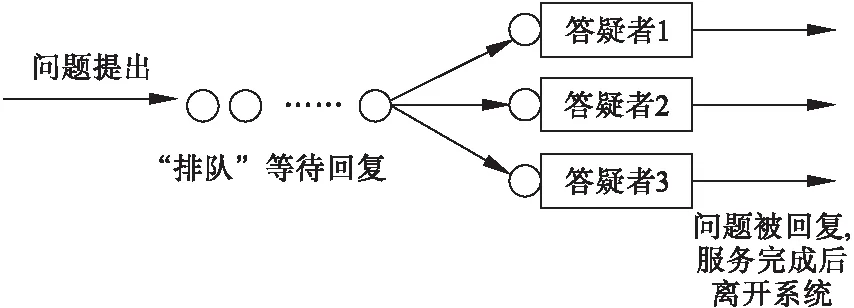
图1 课程中心排队系统示意图

(2)课程中心排队系统的主要参数及其估计

排队服务系统的主要参数包括服务强度(ρc)、问题等待回复的概率(Pwait)和队长(Ls)。

②问题等待回复的概率是指当某个问题被提出来以后,由于各种原因(如问题本身较为复杂,答疑者需要一定的时间理解和解答)导致该问题不能立即被回复、因而需要等待的概率。采用Erlang等待公式[7]可计算问题被提出来后需要等待回复的概率为:

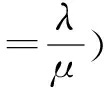
③队长指系统中等待回复的问题的期望值,当队长越小且问题等待回复的概率越低时,排队系统效率更高。平均队长的计算公式为:

(3)课程中课程中心排队系统的优化

本研究以“保持适当的服务强度”作为排队服务系统的主要优化目标。根据国内外的研究显示,当服务强度处于70%～80%时,服务机构能保持最佳的工作水平和服务质量[2]。所以,有必要使系统维持一个合理的服务强度ρc(ρc<1),使得答疑者在学期中能够得到适当的工作量,从而保证其较高的服务效率和服务质量。进一步从服务强度ρc的定义中可以发现,与服务强度相关的指标包括λ,μ和c。其中λ和μ主要与学生的主观能动性有关,而授课团队的人数c则直接与课程中心的建设密切相关。因此,从课程中心建设的角度出发,本研究拟以求解ρc的相对最优值作为实现主要优化目标的手段。另外,考虑到问题等待回复的概率Pwait和队长Ls也与课程中心的建设有关,同时也是c的函数,因此在实现主要优化目标的前提下,本研究还将“限定Pwait和Ls在相对最优范围内”作为次要优化指标。

结 果

1.数据整理

在数据整理阶段,仅筛选出“答疑解惑”类型的帖子进行整理。在此基础上,具体计算两个指标:一个指标是时间上相邻的两个问题的到达时间间隔(以下简称“到达时间间隔”),其计算方式是时间上相邻的两个问题的提出时间之差(为保守起见,不足1天的按0.5天计算)。例如,A问题是在3月24日提出的,当天晚些时候又有B问题被提出,而紧随其后的C问题是在3月25日提出的,那么A和B的到达时间间隔为0.5天,B和C的到达时间间隔则为1天。另一指标是问题从提出到被回复的时间间隔。理论上讲,该时间间隔=该问题从提出到被答疑者开始关注的时间间隔+该问题从被答疑者开始关注到被回复的时间间隔。但在实际操作过程中,由于授课团队的三名成员约定每人至少每半天浏览一次课程中心,加之时间以天为单位,因此一个问题从提出到被答疑者开始关注的时间间隔几乎可以忽略不计。在此情况下,可以近似认为问题从提出到被回复的时间间隔约等于该问题被服务的时间(以下简称“服务时间”)。

2.到达时间间隔规律与服务时间规律

(1)全时段到达时间间隔规律

在课程期间,学生平均每天在课程中心提问的发帖1.232篇,图2展示了从3月12日到5月19日期间,课程中心每天提问的发帖数。由该图可以看出,考试前一天(5月19日)提问发帖数急剧增加,属于离群值,本文不纳入分析。此外,3-4两个月与5月份的到达时间规律差异较大,进一步使用t检验比较3-4月与5月的到达时间间隔与服务时间,发现这两个时段之间差异有统计学意义(到达时间间隔:t=2.32,P=0.0253;服务时间:t=2.31,P=0.0242),故应分段进行分析。

(2)3-4月到达时间间隔规律与服务时间规律

在课程期间,学生平均每天在课程中心提问的发帖1.232篇,图2展示了从3月12日到5月19日期间,课程中心每天提问的发帖数。

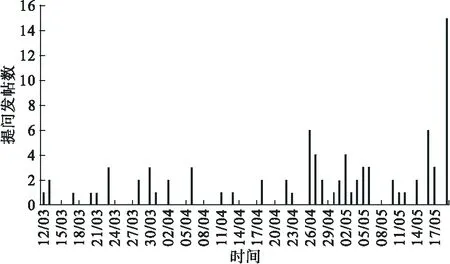
图2 课程中心每天提问发帖数直条图

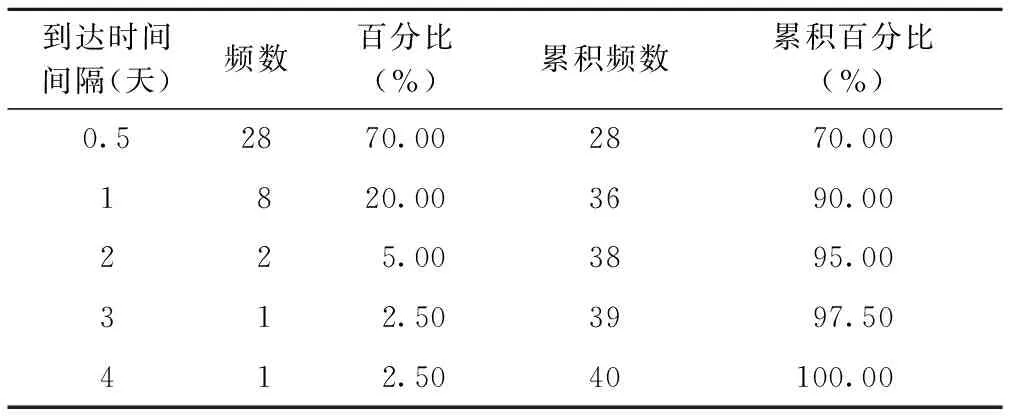
到达时间间隔(天)频数百分比(%)累积频数累积百分比(%)0.52870.002870.001820.003690.00225.003895.00312.503997.50412.5040100.00

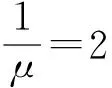
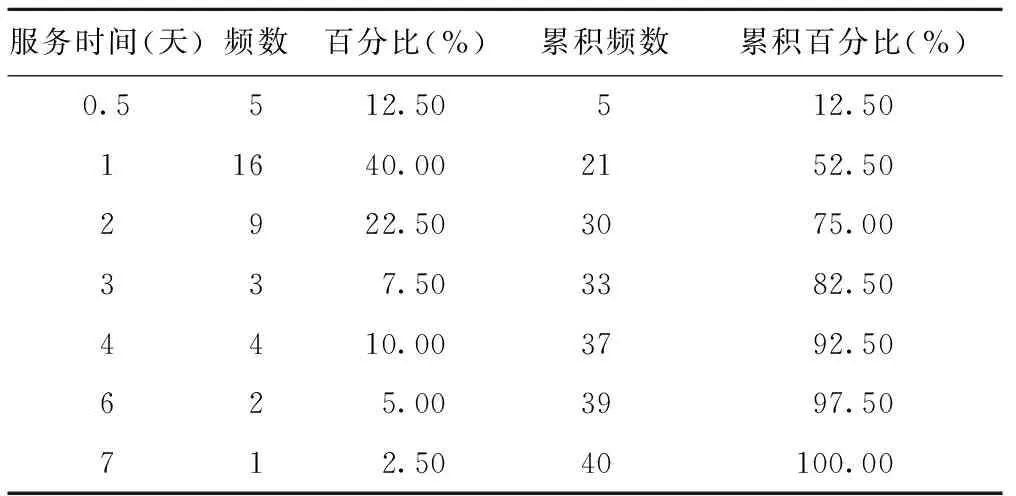
表2 3-4月课程中心服务时间的频数分布表

(3)5月到达时间间隔规律与服务时间规律

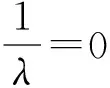
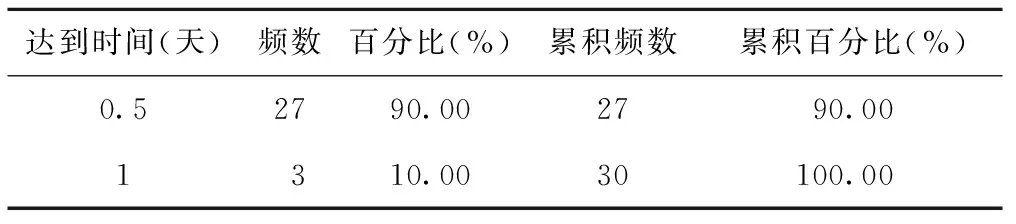
表3 5月课程中心到达时间间隔的频数分布表

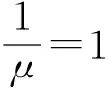
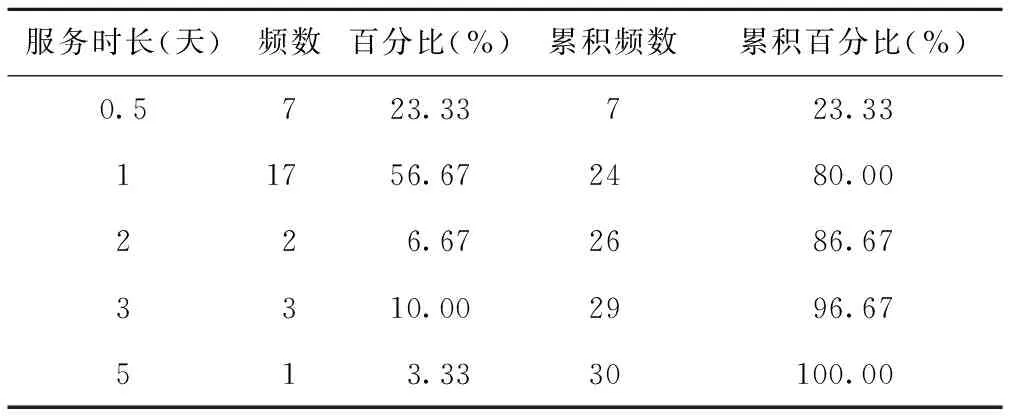
表4 5月课程中心服务时间的频数分布表

3.排队服务系统的主要运行指标及优化设计

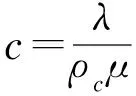
表5 3-4月和5月配置不同授课团队人数时排队服务系统指标

讨 论

本研究首次将排队模型运用到卫生统计学课程中心建设的优化研究中,对课程中心学生的排队系统的结构进行验证和模拟,较好地揭示了学生提问和回复问题的时间分布规律,进而为今后课程教学教师及助教的配备,以及课程中心的优化提供了一定的参考经验。

1.为合理配置教师及助教提供量化依据

根据蒙特卡洛仿真法模拟结果,3-4月份当授课团队配置三人时,教师工作强度为0.83,问题提出后(问题到达课程中心后)平均约4个问题在排队等待,需要等待概率是0.57;当授课团队配置四人时,教师工作强度为0.6,问题提出后平均约2.7个问题在排队等待,需要等待概率是0.27;5月份的结果显示,当授课团队配置三人时,教师工作强度为0.77,问题提出后(到达后)平均约3.7个问题在排队等待,需要等待概率是0.55;当授课团队配置四人时,教师工作强度为0.58,问题提出后平均约2.5个问题在排队等待,需要等待概率是0.24。可以看出,如果授课团队配置四人,则教师工作强度在0.58～0.6,在一定程度上会造成教学资源的浪费,本学期授课团队配置三人(通常一位任课教师和两位助教)时较为合理。

2.根据班级特点动态调整,实现排队系统的优化

本研究展示了如何建立排队论模型,并结合班级特点和调查资料分布特征等情况估计模型参数,从而运用于课程优化设计的整个过程。实际上,通过上述过程可以发现,排队论模型提供了一种操作简单(只需要考虑λ,μ和c等少数几个参数)、易于理解(排队的现象在生活中随处可见)的优化设计方法,除了《卫生统计学》以外,对于其他学科的课程建设也有较高的实用价值。

3.课程中心在线提问系统的优势

课程中心在线提问系统能极大的提高回答问题的效率。鉴于同一门课学生的疑问有共同之处,因此可以在一定程度上避免教师的重复答疑,促进学生间知识共享。从模型的结果可以看出,配置一位任课教师和两位助教教师的情况下,基于课程中心平台问题回答的平均等待时间少于3天,基本能保证学生的问题都能得到及时的回复;而传统意义上,学生在课后学习产生的疑问,往往只能等到下次上课的时候才有机会提问,从而导致一部分同学的问题不能得到及时有效的解决。同时,课程中心能够将问题记录在论坛里,学生长期都能够看到,还可以对提出的问题进行讨论和分享,从而达到“教学相长”的协同效果。

根据全时段到达时间间隔规律部分可以看出,考试前一天(5月19日)提问发帖数急剧增加,这应该与学生“临时抱佛脚”的心态有关。一方面提示今后教学的开展需要更加强化平时的要求;另一方面说明把课程中心作为一种辅助教学手段的同时,还是需要与考前答疑等传统教学手段相结合。综上,网络课程中心作为一种全新的教学方式渗透到高等教育的教学过程中,实现了网络教学与课堂教学的有机结合,这将对学校推进网络平台学习、促进教学质量和提高学生学习效率起到积极作用。