积分补偿随机共振在盾构机轴承故障检测中的应用

梁 波，余振军，蒲凭山，王晓兰

（1.兰州理工大学 电气工程与信息工程学院 电气与控制工程国家级实验教学示范中心，兰州 730050；2.甘肃省工业过程先进控制重点实验室，兰州 730050；3.陇南师范高等专科学校，成县 742500；4.陕西有色天宏瑞科硅材料有限责任公司，榆林 719208）

0 引言

提取故障特征频率是实现轴承故障诊断的重要前提条件，目前常用的方法是通过抑制噪声来提高信号的信噪比，但当故障信号频率和噪声频率接近时，滤除噪声的同时，也可能损害故障信号的质量。另外，设置合适的阈值是进行高品质消噪的基础，但在强噪声干扰下，如何设置合适的消噪阈值也是消噪的难点。

近年来，意大利学者在研究冰川与气候问题时发现，微弱信号在发生随机共振[1,2]条件下，也能产生较高能量输出。研究表明，在一个非线性双稳系统中，当系统输入噪声增加时会发生随机共振现象，使部分噪声能量转化为微弱故障信号能量，极大提高输出信号信噪比[3,4]，并且当噪声强度增加到某一最佳值时，可将输出信号频率峰值最大化[5,6]。然而随机共振仅适用于绝热近似物理条件下的小参数情况[7]，而实际工程问题中信号频率高达上千赫兹，远远超出了随机共振的应用范围。

针对大参数输入信号问题，文献[7,8]提出二次采样随机共振的方法检测微弱信号，该方法的优点是线性压缩实际测得的大参数信号，使之适应随机共振条件下的小参数要求，经双稳态非线性随机共振系统得到响应输出。但是在实际工程应用中，输入信号的各种特征值都是未知数，而进行随机共振必须选择合适的采样频率以及压缩频率，对于大参数信号来说，如何更好的选择合适的二次采样频率需要更进一步的研究。文献[9]提出一阶线性系统调参广义随机共振的特征提取方法，该方法通过调节一阶线性系统参数，可以得到信噪比取极大值的广义随机共振现象。但是该方法仅适用于周期信号与噪声信号作用下的一阶线性系统，而且不能保证输出谱图上特征信号能达到理想的识别性，必须确定合适的采样频率fs和非线性系统结构参数a使信号可识别性最佳。因此，如何选择一个合适的参数a值对特征信号频率的判别有着直接的影响。文献[10]提出基于非线性系统随机共振的方法，该方法可以检测出多频周期性弱信号以及强噪声背景下较大频率的多频周期性信号，同时也能识别和探测某些调制在载波中的弱信号。但是这些信号频率基本上都在1Hz以下，远远低于工程上高频信号的频率，所以该方法不能使高频信号产生随机共振响应。

本文在以上研究的基础上，综合随机共振方法的检测特点，针对大参数信号难以实现随机共振的问题，提出了一种基于积分补偿调节大参数的随机共振方法，并在轴承故障信号检测中加以应用，同时在LabVIEW软件环境下，编写故障诊断程序，实现信号采集、特征提取、故障判断等功能，仿真及实验验证了理论方法的可行性。

1 基于积分补偿调节大参数的随机共振的轴承故障诊断原理

1.1 基本原理

积分补偿调节参数的随机共振故障诊断流程图如图1所示，首先由AD采集轴承振动信息，获取轴承振动信号角频率，即补偿系数；其次对随机共振系统的非线性方程进行相应的积分补偿，并建立新的非线性随机共振系统模型，同时重新运行新建立的系统模型进行随机共振，并得到系统输出信号；最后对输出信号进行FFT变换，得到轴承故障振动信号的频谱，再对AD采集的轴承故障信号进行特征频率计算，将计算出的特征频率值和输出信号的FFT频谱进行对比分析并诊断出故障类型。

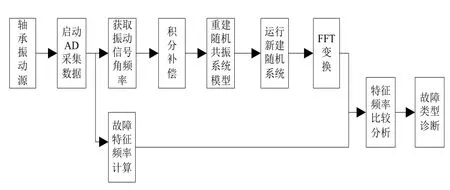
图1 积分补偿调参数的故障诊断流程图

1.2 滚动轴承故障特征频率

盾构机主轴承是典型的滚动轴承，其常见的失效方式包括磨损、疲劳腐蚀、压痕和胶合失效等。滚动轴承在运动过程中失效造成的损伤或缺陷必然会使其产生一定频率的宽带冲击[11]。通常将这种冲击称为轴承的故障特征频率，其一般处于低频，是进行故障诊断的重要信息特征之一。轴承各元件的故障特征频率按下式计算。

外圈故障频率f0：

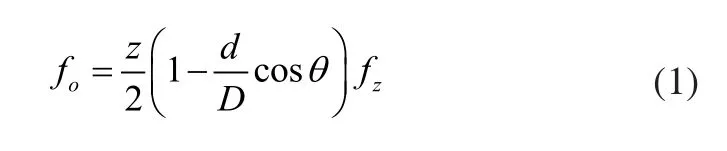
内圈故障频率fi：

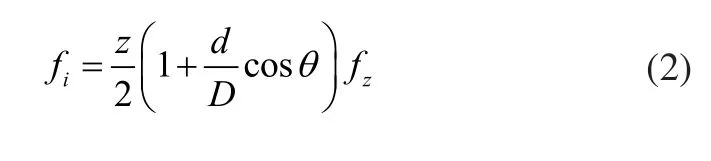
滚动体故障频率fb：

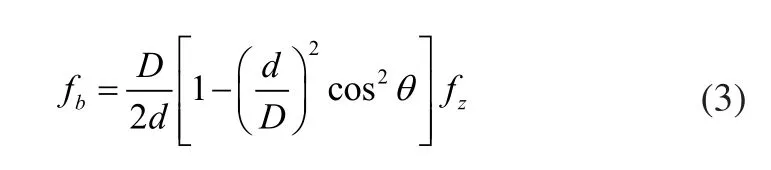
式中：fz为转频；D为轴承节径；d为滚动体直径；z为滚动体个数；θ为接触角。

1.3 随机共振原理

非线性系统在一定条件下，高频噪声的部分能量可以转移到低频信号中，从而提高信噪比达到微弱信号检测的目的，该协作效应称为随机共振。双稳态随机共振系统的数学模型可以用郎之万（Langevin）方程来描述[12]；

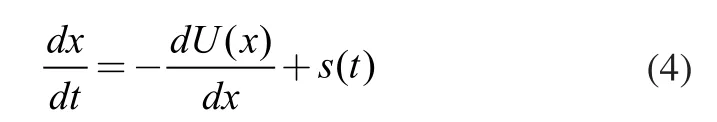
通常势函数U(x)的表达式如下：

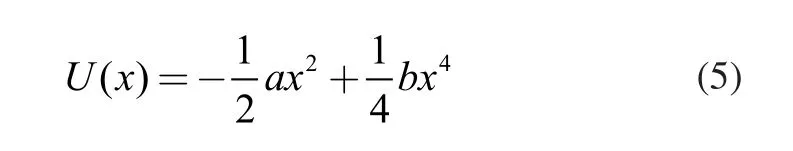
s(t)为含有噪声的微弱信号，可表示如下：

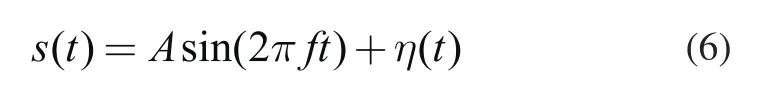
将势函数式(5)和输入信号式(6)代入式(4)中得：

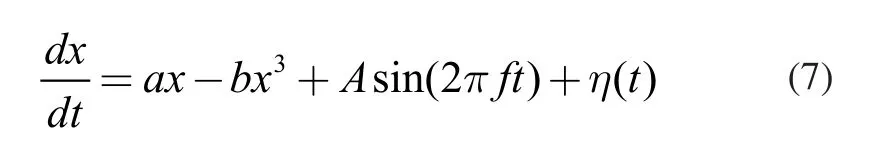
式中，a、b为非线性双稳系统的结构参数；通常a=1，b=1，A为信号幅值，f为信号频率；为白噪声，且满足：

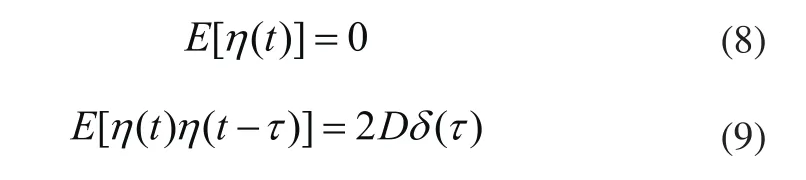
式中D为噪声强度。

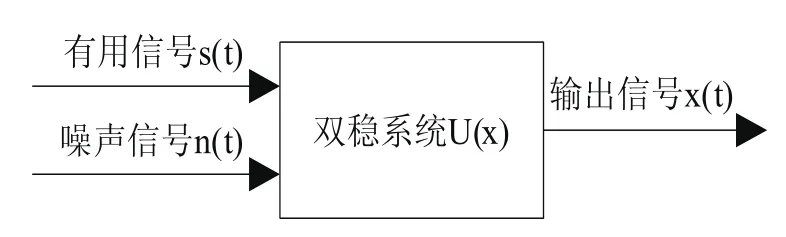
图2 双稳随机共振系统

因此随机共振的产生需要满足2个条件：

1）由噪声引起的平衡态间的跳变必须与输入信号周期同步，即为Kramers逃逸率。

2）弱信号的幅度A与临界值Ac相比不能太小，否则即便在噪声帮助下仍不能克服势垒而发生随机共振。

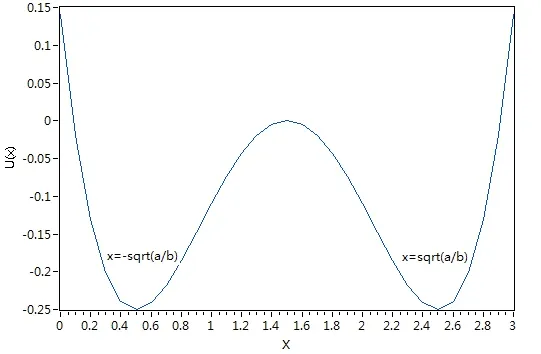
图3 势函数U(x)

令式(7)中a=1，b=1，A=0.03，f=0.01Hz，且噪声强度D=0.03，采样频率fs=5Hz，建立随机共振系统模型。利用四阶龙格库塔法对式(1)进行求解，并作时域和频域分析。系统输入信号和输出信号的时域波形图以及FFT变换后的频谱图分别如图4和图5所示。

从图4(a)可以看出，该时域信号为非线性随机共振输入信号和噪声信号的混叠，并且输入信号被噪声信号完全淹没，对该时域信号作FFT变换，得其频谱如图4(b)所示，可见当噪声信号干扰较小时，在0.01Hz处存在幅值较小的谱峰。若将图4(a)中信号通过随机共振系统进行处理，可以得到如图5(a)所示的时域正弦波形，对其作FFT变换，得其频谱如图5(b)所示，可见0.01Hz处出现的谱峰幅值较随机共振之前明显增大，随机共振对系统信噪比的优化显而易见。

然而，对于不同的输入信号，非线性随机共振系统不可能都能趋近随机共振状态，因此需要对于随机共振系统自身的参数进行调节从而使系统能对不同的输入信号进行理想的随机共振响应。

1.4 积分补偿原理

由于一般非线性系统（参数a=1，b=1）中存在阻尼，且从Kramers逃逸率rk的表达式可以看出，rk不能突破极限值因此该系统无法对高频信号进行提取，只能与0＜f＜0.112Hz的小参数信号产生随机共振。

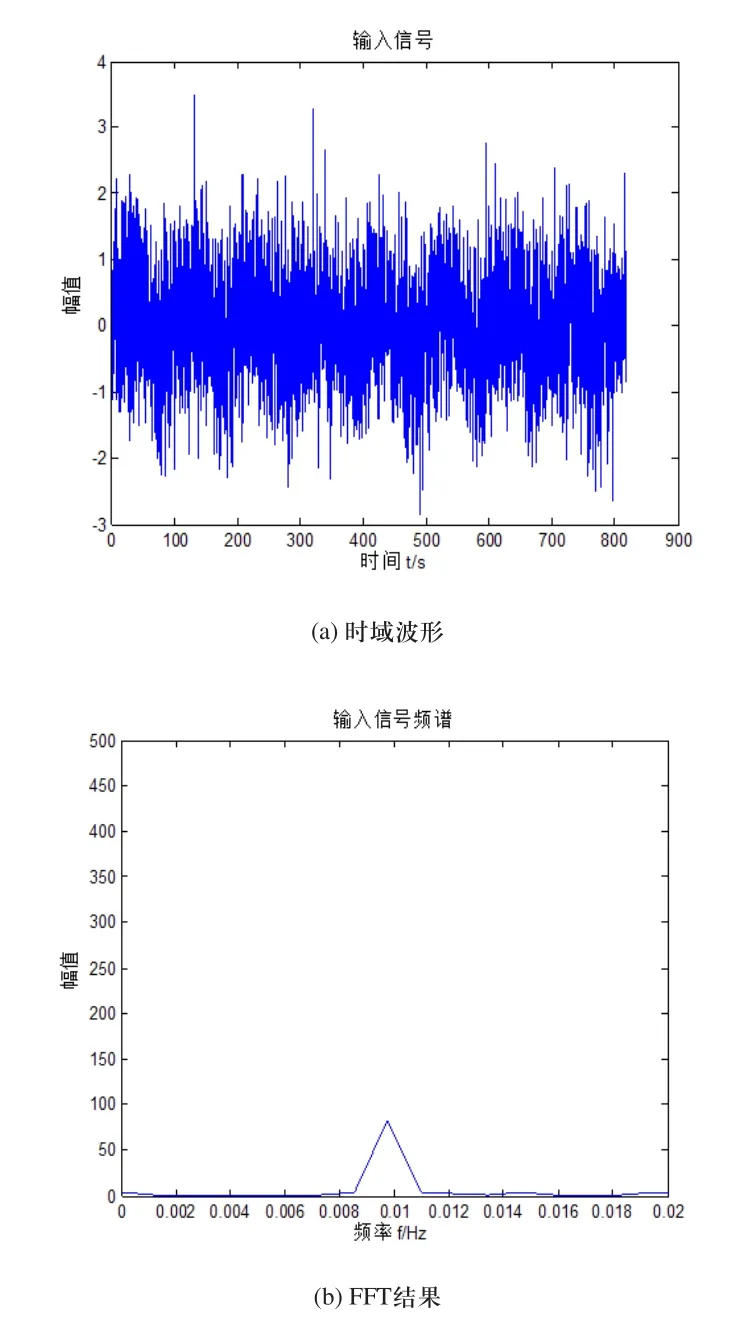
图4 输入信号时域图和频谱图

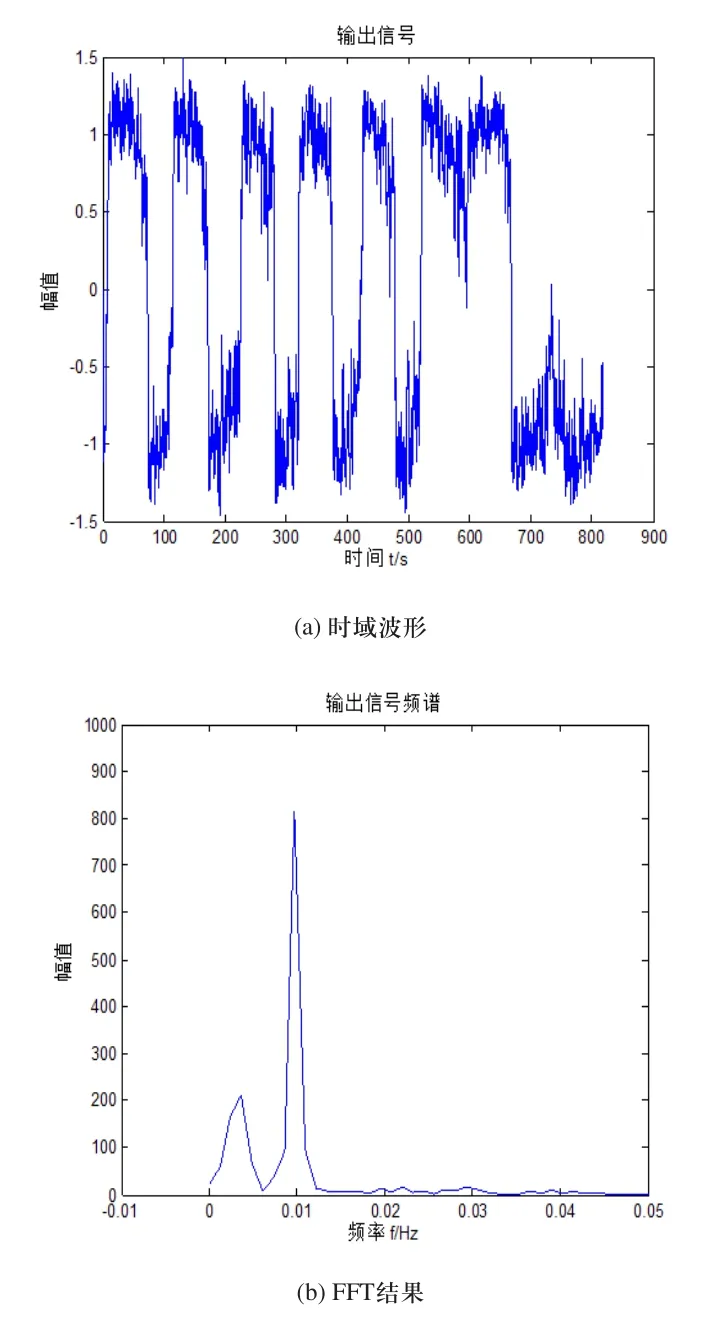
图5 输出信号时域图和频谱图

大量的仿真数据表明，在没有满足随机共振小参数信号的条件下，输入信号的频率越高，系统阻尼比越大，对应输出信号频谱幅值就越低，系统也不会产生随机共振。从式(7)中可以看出，在系统模型中周期信号被直接输入到状态导数dx上，所以阻尼对于系统的作用其实是一个积分环节，此时系统输出信号的幅值将变为原输入信号幅值的倍，其中正弦信号的角频率为ω。表达式如下：

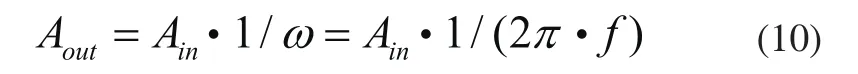
由式(10)可得输入信号频率越高，其输出幅值越低，能量衰减也越严重，所以输入的大参数信号没有足够的能量穿越双稳态非线性系统的势垒，从而不能使系统达到随机共振状态。

由于随机共振方法在大参数信号检测应用中的局限性，本文采用“积分补偿”的思想来实现工程实践中大参数信号的随机共振。所谓积分补偿随机共振，即在系统上增加一个放大环节抵消阻尼对输入信号的衰减作用，使得输入信号能够穿越双稳态系统的壁垒。具体方法是在式(1)的基础上增加放大环节Gain，对该系统进行相应的积分补偿：

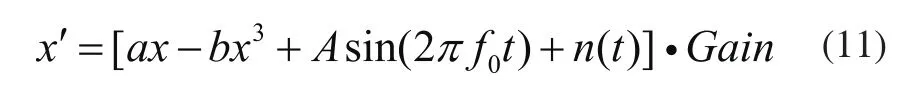
由式(11)积分补偿方程再次建立新的非线性随机共振系统模型，同时将放大环节的Gain值赋值为原输入信号f的2π倍，对其衰减程度进行相应的补偿，同时应用新建立的系统模型进行随机共振。此时大参数信号可满足或接近随机共振所要求的小参数前提条件，实现大参数信号的随机共振。

2 积分补偿调节大参数随机共振检测方案的实现

外部通过加速度传感器测量旋转机械振动，振动信号经过AD模块转换为对应数字量并通过USB接口送入上位机。上位机采用LabVIEW完成基于积分补偿调节大参数随机共振方法的主轴承故障诊断程序，程序流程如图6所示。

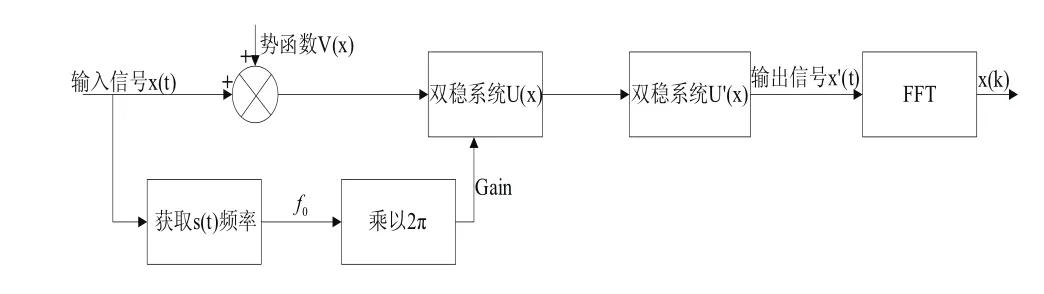
图6 积分补偿调节大参数随机共振法流程图

积分补偿具体运算过程如下：

1）用LabVIEW的输入信号为x(t)和势函数V(x)建立双稳随机共振系统U(x)。

2）从输入信号中获取有用信号s(t)的频率f，并乘以2π，得到积分补偿系数Gain。

3）给1）中建立的系统U(x)乘以补偿系数Gain，并建立新的双稳系统U′(x)。

4）启动双稳系统U′(x)，产生随机共振，并输出信号x′(t)。

5）输出信号x′(t)进行FFT变换，获得x′(t)的频谱x(k)。

6）将输出信号的频谱x(k)谱峰的频频率和计算出的故障特征频率进行对比分析，诊断出轴承故障类型。

3 基于随机共振方法的信号仿真分析

假设(7)式中的参数分别为a=1，b=1，A=0.31，f=40Hz，D=0.31，仿真采样频率fs=2000Hz，采样点数N=4000，数值计算步长Ts=h=0.0125。信号经图2随机共振系统得到输出响应，并作时域和频域分析。输入信号的时域波形图和频谱如图7、图8所示，信号经过积分补偿调参随机共振系统后的时域波形图和频谱如图9、图10所示。

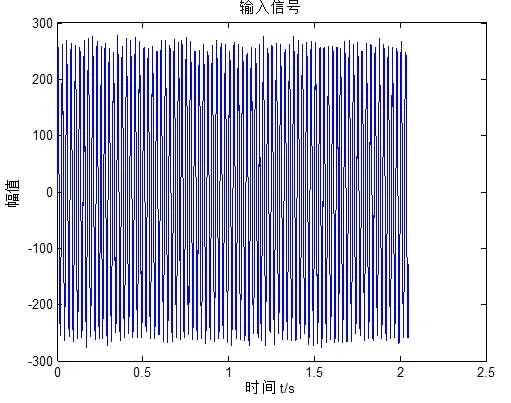
图7 输入信号的时域波形图

图8 输入信号的频谱图

从原始信号的时域图和频谱上可以看出信号完全无法识别。但是经过积分补偿随机共振系统后，时域图具有了一定的周期性，并且频谱图上谱峰最大的点对应的频率为40Hz。

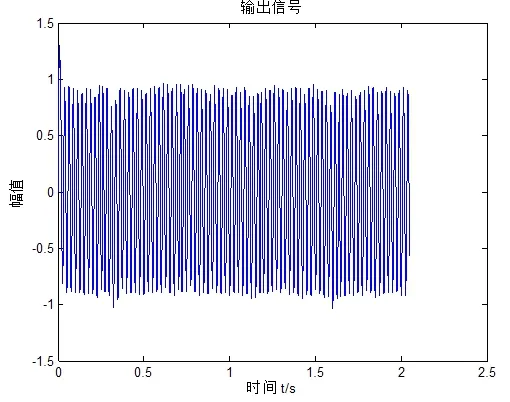
图9 输出信号的时域波形图

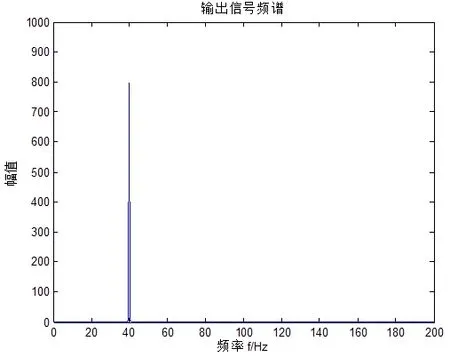
图10 输出信号的频谱图

4 随机共振方法在轴承故障分析中的应用

对于施工中的盾构机，较重的负荷使轴承易出现多种故障。但其故障初期的特征信号比较微弱，往往被工作环境中的各种噪声所淹没，因此可利用随机共振方法进行特征信号提取。

实验对象选用6205-2RS深沟球轴承，其滚动体直径为7.94mm，轴承节径为39.03mm，滚动体个数为9个，接触角为0o。使用电火花加工技术在轴承外圈滚道上布置故障直径为0.18mm的故障点来模拟滚动轴承的外圈故障。试验时轴承转速为1797r/min，信号采样频率为20kHz，分析频率为10kHz，基本采样点数N=3072，采样时模拟抗混滤波器的截止频率为3kHz，包络分析时带通滤波器的通带为4～10kHz。由轴承参数以及故障特征频率公式计算可得，轴承外圈故障特征频率为107.573Hz。同时为了模拟实际工况，给实验数据增加噪声强度D=2的高斯白噪声，图11为加噪后轴承发生外圈故障时加速度传感器所采集的径向振动信号，图12是该信号的FFT分析结果，其低频信号幅值较小，并存在较大的噪声干扰，不利于故障诊断。

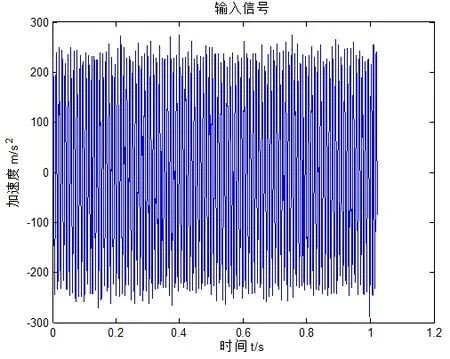
图11 轴承故障时径向加噪振动信号

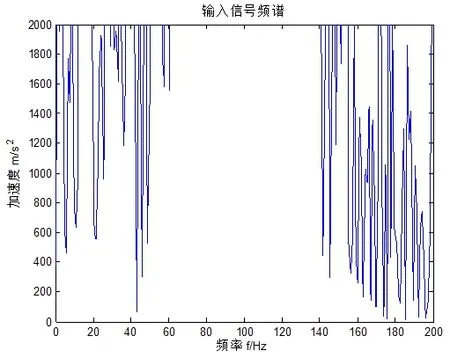
图12 轴承故障时径向加噪振动信号FFT频谱

现对原输入信号进行积分补偿调节大参数，随机共振系统参数设置如下：a=0.1，b=1，系统的积分补偿系数为Gain=2πf≈675.6，噪声强度D=2，数值计算步长h=0.00005。信号经过积分补偿调节参数随机共振后的输出信号的时域图和频谱图如图13、图14所示。

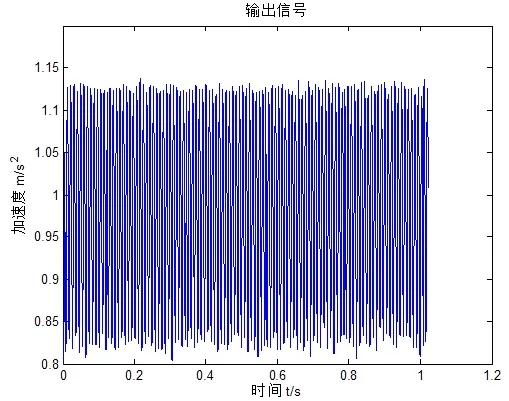
图13 积分补偿调节参数后的轴承故障时径向输出信号时域图

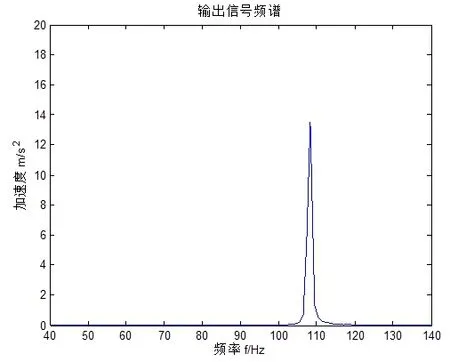
图14 积分补偿调节参数后的轴承故障时径向输出信号的频谱图

对比图12与图14可以明显地看出：图14中滚动轴承外圈特征频率处存在很明显的冲击性峰谱线，同上述理论分析的故障特征频率f=107.573Hz基本吻合，从而验证了积分补偿调节大参数的随机共振方法的有效性。

5 结论

由于主轴承振动信号为大参数信号，FFT方法难以识别幅值较小的故障频率成分。而普通随机共振系统在具有阻尼的情况下会对大参数信号幅值产生严重衰减作用，从而难以实现大参数信号的随机共振并提取轴承故障特征频率。本文针对此问题，采用积分补偿调节大参数的随机共振方法对故障特征频率进行提取，仿真与实验证明了本方法的有效性。