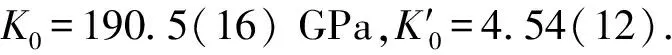高压下铬的状态方程和强度研究*

熊 伦 李 斌 刘 景

(1．四川文理学院智能制造学院，四川 达州 635000； 2．达州智能制造产业技术研究院，四川 达州 635000； 3．中国科学院高能物理研究所，北京 100049)

0 引 言

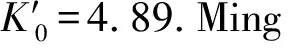
需要注意的是，文献报道[1-4]的体弹模量存在差异.体弹模量的确定非常依赖于静水压状况[5].由于传压介质的固化，没有传压介质能在压力超过15 GPa以后还能提供完全的静水压环境[6-9].以He作为传压介质可以非常好地达到真实的热动力学状态，因为它帮助减小由于剪切力而引起的效应[10].另一方面，尽管有一些对铬的状态方程研究的文献，但是到目前为止，还没有文献对其强度进行研究.

本文中，用角散径向衍射技术在准静水压环境以He作为传压介质研究压力加到47 GPa，得到了压力-体积(P-V)压缩曲线.此外，利用角散径向衍射技术研究了铬到68 GPa的强度.

1 实验设计

铬样品购买于阿法埃莎(Alfa Aesar)公司，颗粒粒度小于22 μm，样品的纯度是99.2%.对于角散轴向X射线衍射实验，用台面大小为300 μm的改进型的Mao-Bell 金刚石对顶砧.对于充氦气(He)的准静水压实验，T301封垫被预压到约35 μm厚度，并在压痕中间打直径为160 μm的样品孔.40～50 μm大小的样品片被放到样品孔中心位置，再放上一颗大小约为10 μm的红宝石作为压标[11].用气体加压装置加到30 000 psi高压(等价于0.165 GPa)，取出后再用机械装置对DAC进行手动加压到3 GPa.

选用台面直径为300 μm的两柱全景DAC进行径向衍射实验.预压Be封垫到约25 μm厚度，在压痕的正中间打大小为60 μm的样品孔.样品被压片，再被填入到样品孔中.在样品表面的中间位置装入直径为10 μm的红宝石作为压标[11].选择红宝石，是因为其没有衍射峰，从而可以避免衍射峰重叠.为了增大剪切力，径向衍射实验不加传压介质.实验中DAC转过28°以减小Be封垫的衍射峰影响[12].

轴向衍射实验和径向衍射实验均在北京同步辐射装置的4W2实验站上进行，实验的单色光波长是0.619 9 Å，半高全宽分别是30 μm(水平)和12μm(垂直).衍射谱由Mar345成像板接收，接收到的数据由Fit2D软件[13]进行分析，距离和角度由CeO2进行标定.径向衍射每个压力点在采谱前先放置30 min使样品中的应力充分释放，随后采谱，采谱时间为15～20 min.轴向衍射技术的曝光时间为7 min.

2 理论介绍

X射线径向衍射数据用Singh,Singh[14]和Balasingh[15]提出的晶格应变理论进行分析.根据该理论，测得的dm(hkl)是Ψ角(金刚石对顶砧加压方向和hkl衍射面法向的夹角)的函数，可以表示为：

dm(hkl)=dp(hkl)[1+(1-3cos2ψ)Q(hkl)]，

(1)

其中dm(hkl)是测得的d值，dp(hkl)是静水压环境下的d值.

公式(1)中的Ψ表示为：

cosψhkl=sinβcosδcosθhkl+cosβsinθhkl，

(2)

其中θ是衍射角，δ是成像板中的几何角度，β等于28°(径向衍射实验将DAC转过28°).

公式(1)中的Q(hkl) 是晶格应变，可以表示为：

(1-α)(2GV)-1}，

(3)

G是剪切模量，下标R和V分别表示Reuss近似(压力连续)和Voigt近似(应变连续).上标X表示由于不同的hkl引起的平均效应.a确定了Reuss近似和Voigt近似的比重.在绝大多数高压实验中，令a=1.由此，差应力的公式[16]可以推导出来：

t=6G，

(4)

表示所有Q(hkl) 的平均值.G是粉末样品的剪切模量，而且G可由超声波结果外推和理论计算得到.

3 结果与讨论

对于准静水压实验，衍射谱的一维积分图见图1.图中可以看到铬的三个峰(110)、(200)、(211)一直存在，而且铬一直保持bcc结构到实验的最高压力47 GPa.

图1 轴向衍射准静水压实验的衍射谱积分图

对于径向衍射实验，采集得到的衍射谱用Fit2D软件[13]处理，再用Multifuit4.2[17]软件进行进一步分析.选择衍射环从90°到180°，每5°进行积分.铬的径向衍射实验研究到68 GPa，压力由红宝石压标[11]给出.图2为径向衍射不同压力下ψ=54.7°时的衍射谱积分图.图中可以观察到铬的bcc结构的四个峰(110)、(200)、(211)、(220)在整个压力范围内一直存在，实验压力范围内没有发生相变.衍射峰位由Multifit 4.2[17]用Pseudo-Voigt函数拟合得到.

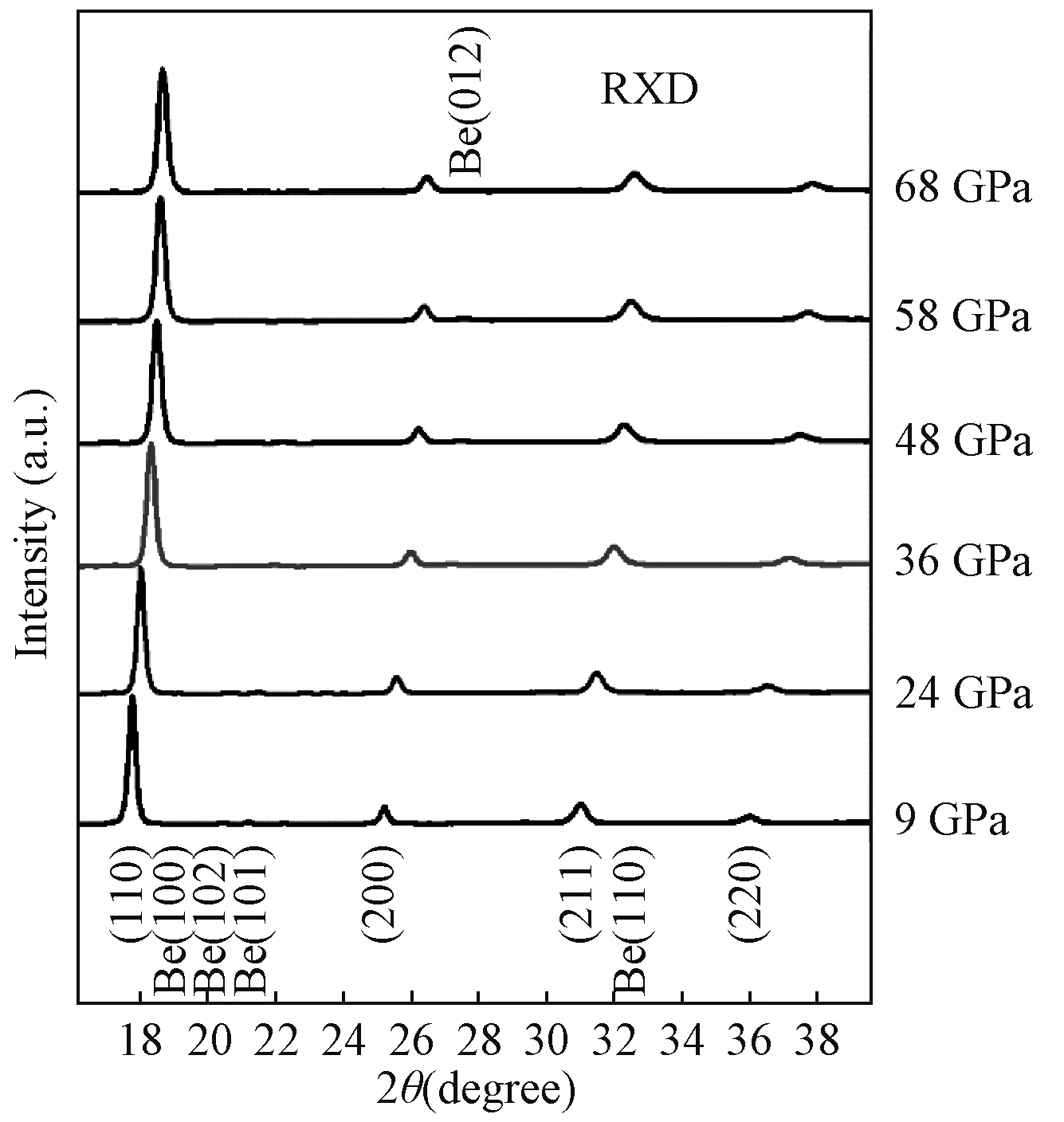
图2 径向衍射在各压力下ψ=54.7°时的衍射谱积分图

对dm(hkl)随1-3cos2ψ的变化关系进行线性拟合，拟合图见图3.可以看出，拟合结果符合晶格应变理论[14-15]提出的线性关系.

图3 dm(110)随1-3cos2ψ 变化的线性拟合图

对于角度色散X射线衍射(ADXRD)实验，晶胞参数由GSAS软件[18]的Le-Bail精修得到.轴向衍射实验的P-V压缩曲线见图4，作为比较，早期的轴向XRD数据[3-4]也被放到图4中.

体积随压力的变化关系由三阶Brich-Murnaghan方程拟合，其中三阶Brich-Murnaghan方程表示为[19]：

(5)

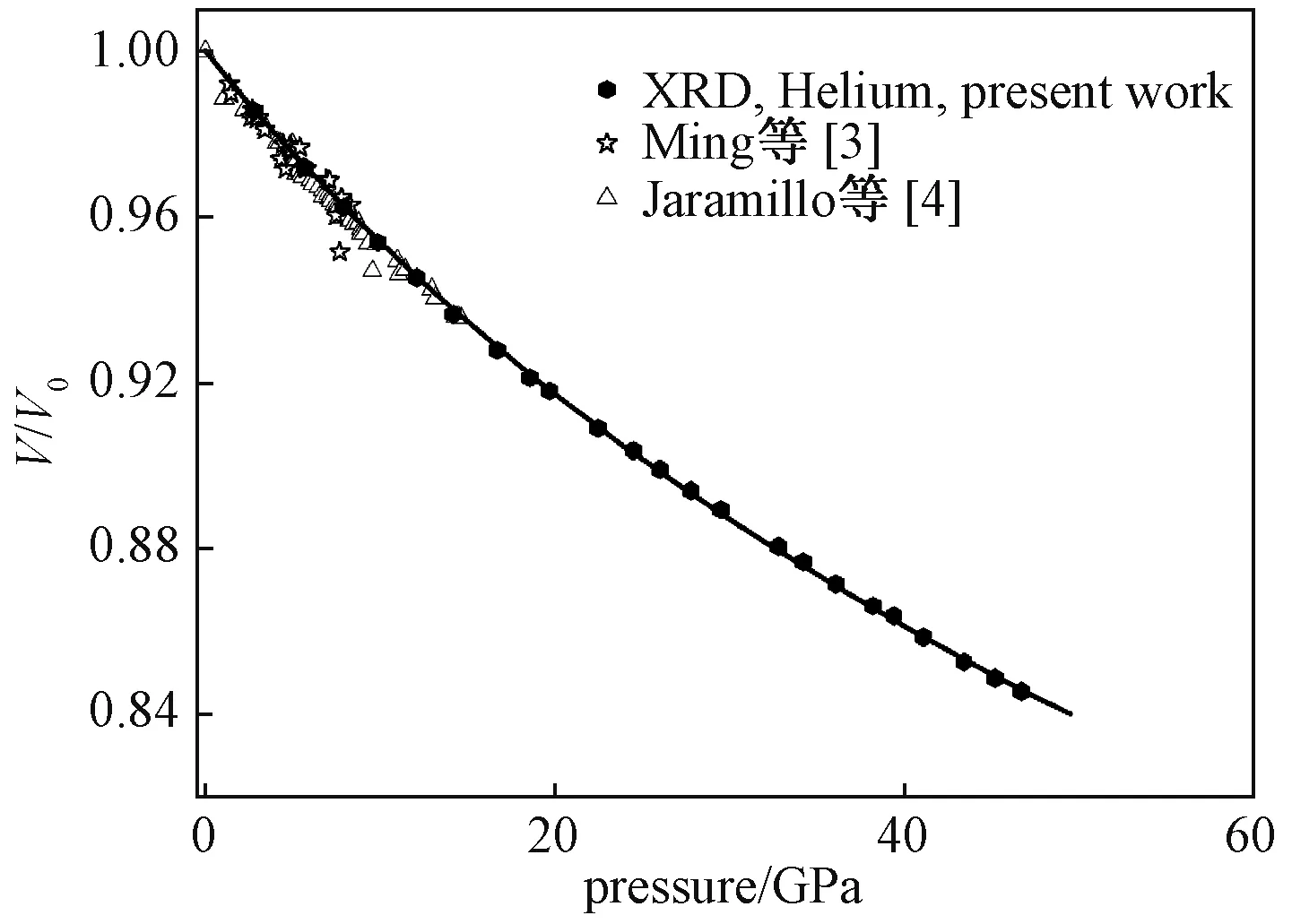
图4 P-V压缩曲线

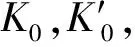
表1 本实验拟合得到的以及文献中的体弹模量及其一阶导数对比.星号表示由晶胞参数的一阶Birch方程拟合得到的结果；酒精表示体积比为4∶1的甲醇乙醇混合液

由线性拟合可以得到Q(hkl)，然后对所有的峰取平均可以得到t/G.图5是铬的P-t/G图.从图中可以看出，t/G在超过19 GPa后变得平坦，表明此时铬由于屈服发生塑性形变，此时t/G的数值为0.005.

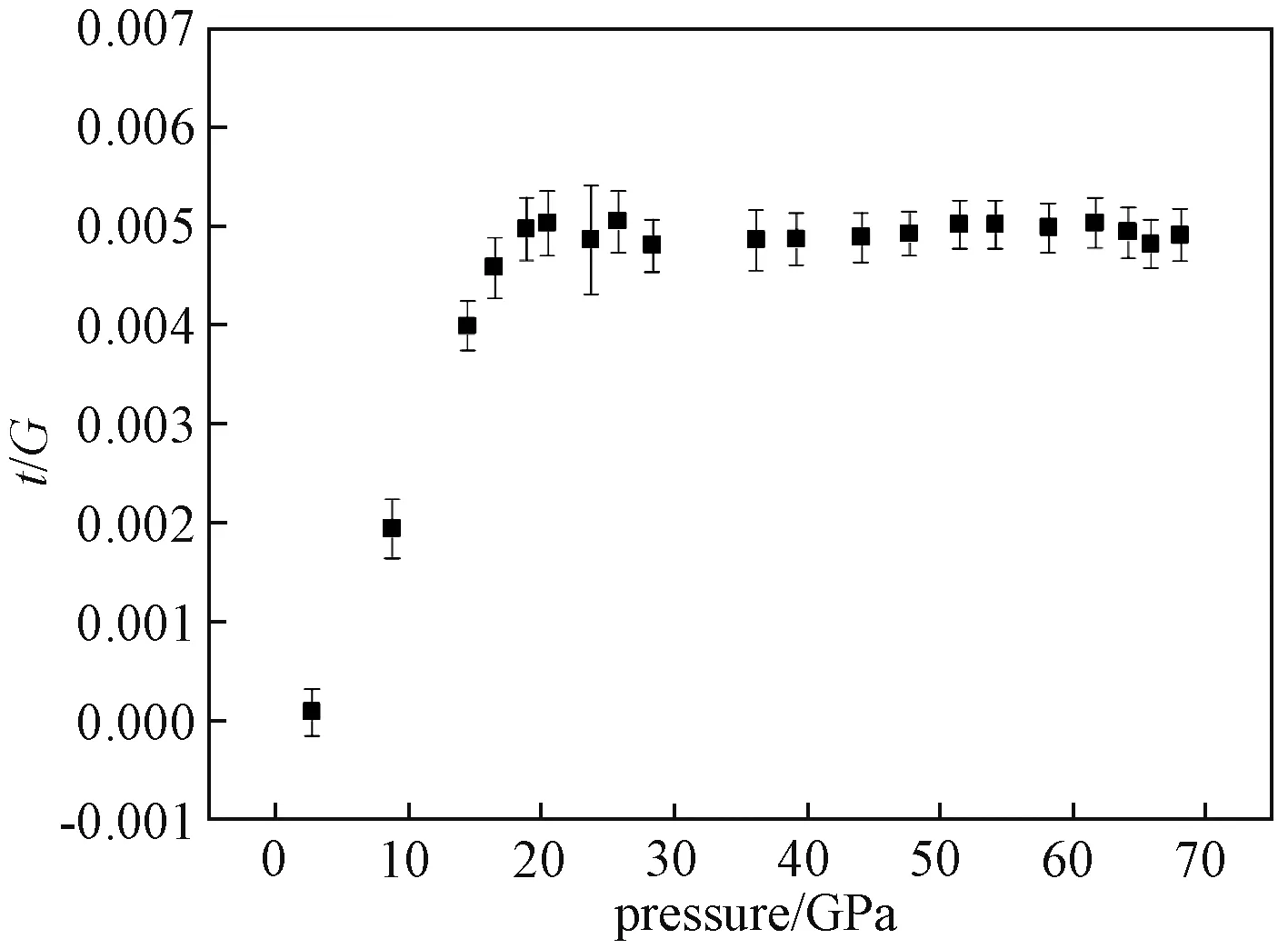
图5 t/G随压力的变化图

图6 铬的差应力随压力的变化图

如果知道高压下的剪切模量，每个压力点的差应力可以由公式(4)得出.对于多晶样品，高压下的剪切模量G可以由以下公式[20]得出：

(6)

此处f=12[(V0/V)2/3-1]，K0和G0分别是室压下的体弹模量和剪切模量.利用铬常压时的剪切模量和其一阶导数[21]，根据公式(6)可以求出铬在高压下的剪切模量.

图6表示铬的剪切力随压力(P-t)的变化关系图.从3～19 GPa，剪切力可以拟合为：t=-0.122(25)+0.046(2)P(GPa).可以看到，在超过19 GPa后，t变化非常缓慢，说明此时铬由于塑性形变而达到屈服，此时的剪切力为0.72 GPa.在68 GPa时，差应力达到最大值，且为0.95 GPa.

4 结 论