莽草酸分子活性及光谱的密度泛函研究

龙 威

(广东石油化工学院化学工程学院，广东 茂名 525000)

八角是我国南方大陆地区广泛生长在湿润、温暖半阴环境中的一种常绿乔木，高可至20 m，树皮灰色或红褐色，又名八角茴香，是我国烹饪行业最典型的食用级香料之一，也是肉类食物常用的调味品[1]. 莽草酸则是存在于八角的干燥成熟果实中的一种重要成分，CAS号为138-59-0，化学名为3,4,5-三羟基-1-环己烯-1-羧酸，其化学式为C7H10O5，属于一种多元烯醇酸的有机化合物[2]. 药理上，莽草酸分子通过影响花生四烯酸代谢，抑制血小板聚集，抑制动、静脉血栓及脑血栓形成，具有抗炎、镇痛作用，可作为抗病毒和抗癌药物中间体，受到了医学界的关注[3-6].

莽草酸的另一种用途就是制备抗亚洲禽流感病毒药物，它被医学称为世界上对付禽流感的唯一武器[7]. 八角茴香在药学界引起轰动，是因为其中的莽草酸可制备成达菲，从而有效地抑制H5N1型禽流感病毒的扩散[8-10]. 法国茴香酒制造商阿尔贝·埃尔格里西这样声称：治疗一位感染禽流感患者需要10粒达菲，等同于13 g八角茴香. 因此，莽草酸的药用价值巨大，每公斤的价格在200美元左右，质量特别好的高达50美元/g. 莽草酸对人的心血管疾病也有明显的疗效，马怡和孙建宁[11]通过实验发现三乙酰莽草酸和异亚丙基莽草酸分子均有明显的抗血栓形成和抑制血小板聚集作用，脱氢奎尼酸(DHQ)与莽草酸脱氢酶(SDH)联合形成DHQ-SDH双功能酶，可增加人体内代谢物从DHQ到SDH域的转移效率，维护心血管的健康.

图1(a)为八角茴香的实体图，它生长快速产量高，且不易生虫害；图1(b)为莽草酸的平面分子结构图，六元环上有一个碳碳双键，环外连接有3个羟基和1个羧基.

莽草酸的药理价值巨大，从植物体八角出发，经过化学分离和提取工艺获得莽草酸的研究受到了广泛的研究和关注[12-13]. 如：王晓强等[14]通过实验树立了一种有效的高效液相法能准确地测定八角属部分植物果实中莽草酸的含量；刘东彦等[15]则利用了大孔吸附树脂能实现纯化雪松松针中的莽草酸和总黄酮，并且有利于莽草酸的进一步分离；国外的Mardones等[16]发明了一种毛细管区带电泳和液相色谱联用方法测定了莽草酸的含量；Bhadra等[17]则发现了八角茴香标准化提取物莽草酸可以高效地发挥抗胆碱酯酶活性；Kim和Park等[18]则利用莽草酸有效地合成了一种新药磷酸奥司他韦，这种药物可以取代达菲而发挥同样的效果；Postina等[19]则通过医学实验发现利用莽草酸可形成解聚素金属蛋白酶，进而可预防阿尔茨海默病，降低淀粉样斑块的形成，减少相关疾病缺陷. 因此，莽草酸已在国际科技上具有重要的地位，除了药理用途外，还可以广泛地运用于电解原理[20]、工业滤膜[21]及高分子薄膜复合材料[22]等领域. 对应而言，莽草酸独特结构分子的性质，在量化计算理论研究领域尚未有报道，本文拟从化学理论计算和分子模拟的角度出发，探讨莽草酸分子的活性、分子光谱等性质，有利于科学解释分子活性，进一步指导后续实验，具备重要的理论指导意义.

图1 植物八角及莽草酸的平面结构

1 研究方法

基于前期对分子活性和分子光谱的研究基础[23-24]，本研究采用相似的方法对莽草酸分子进行了理论计算研究. 分子构型、红外光谱IR、核磁共振氢谱等计算全部在Gaussian03程序[25]中完成.计算中选择密度泛函(B3LYP)方法，基组水平为6-311+g,d(p)，由于分子中所有原子为非金属原子，所以无需考虑赝势，但所有计算均是考虑极化连续介质模型(PCM)，溶剂为水. 根据理论计算模型基本原理，基态分子构型优化后均匹配进行了Freq的振动分析验证，所有的频率均为正值，表明本研究选择的计算对象是势能面上稳定的点. 频率计算的相对校正因子为0.960 3，相对能量的计算均考虑了零点能校正能误差. 考虑概念密度泛函方法在预测化学反应活性和局域选择性方面，无论是在理论上还是在实践上，都是非常有效的[26]. 在DFRT 框架中，全局性反应活性指数如化学势(μ)和化学硬度(η)可分别表示为：

μ=-χ=(∂E/∂N)ν,

η=(∂2E/∂N2)ν=(∂μ/∂N)ν

式中,E为体系的总能量，N是体系的电子总数，ν为外部势能，μ可定义为电负性χ的负值. 根据Mulliken原理[27]，μ=-χ=-(I+A)/2. 而Pearson[28]认为，η=I-A，其中I和A分别是第一电离势和电子亲和势. 根据Koopman的闭壳层理论，I≈-EHOMO，A≈-ELUMO，其中EHOMO为分子最高占据轨道(HOMO)能量，ELUMO为分子最低空轨道(LUMO)能量.Liu[29]提出了亲电性指数ω，ω=μ2/2η，及亲核力差值指数ΔEn=-A+ω=(μ+η)2/2η，亲电力差值指数ΔEe=I+ω=(μ-η)2/2η.

定域反应活性指数应用Fukui函数分别是电子密度ρ(r)对电子数N的一阶微商[30]. 因为f(r)=(∂ρ(r)/∂N)ν；由于Fukui函数是非连续性的，运用有限差分近似方法简化亲电Fukui函数f-(r)、亲核Fukui函数f+(r)，可以获得：f-(r)=ρN(r)-ρN-1(r)；f+(r)=ρN+1(r)-ρN(r)，在式中ρN(r)、ρN-1(r)、ρN+1(r)分别是中性分子、阳离子和阴离子的电子密度[31]. 主要的计算工作在单机微型计算服务器上完成，部分计算借助了中科院超算远程计算格点Ggrid服务完成，部分图像处理借助Multiwfn 3.3程序[32]进行分析和绘制.

2 结果与讨论

2.1 分子构型分析

基态分子的构型如图2所示，八角主要成分莽草酸(shikimic acid)，其分子内原子编号如图2所示. 莽草酸分子是由一个六元碳环和醇羟基、羧羟基共同结合，这种扭曲式的分子结构，使得分子不能实现所有原子共平面，左侧的三个羟基并非同时向上，O(12)呈现向下弯曲，而O(10)和O(11)原子超向平面上方，分子中存在着一定的不饱和结构，依据原子编号，将构型优化计算得到的键长、键角、二面角数据列于表1.

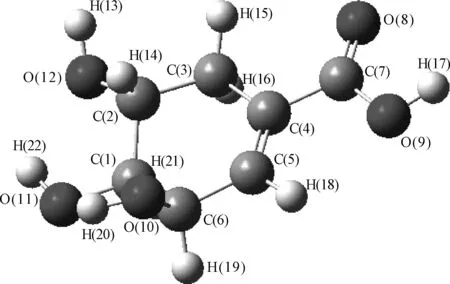
图2 莽草酸的分子结构和原子编号

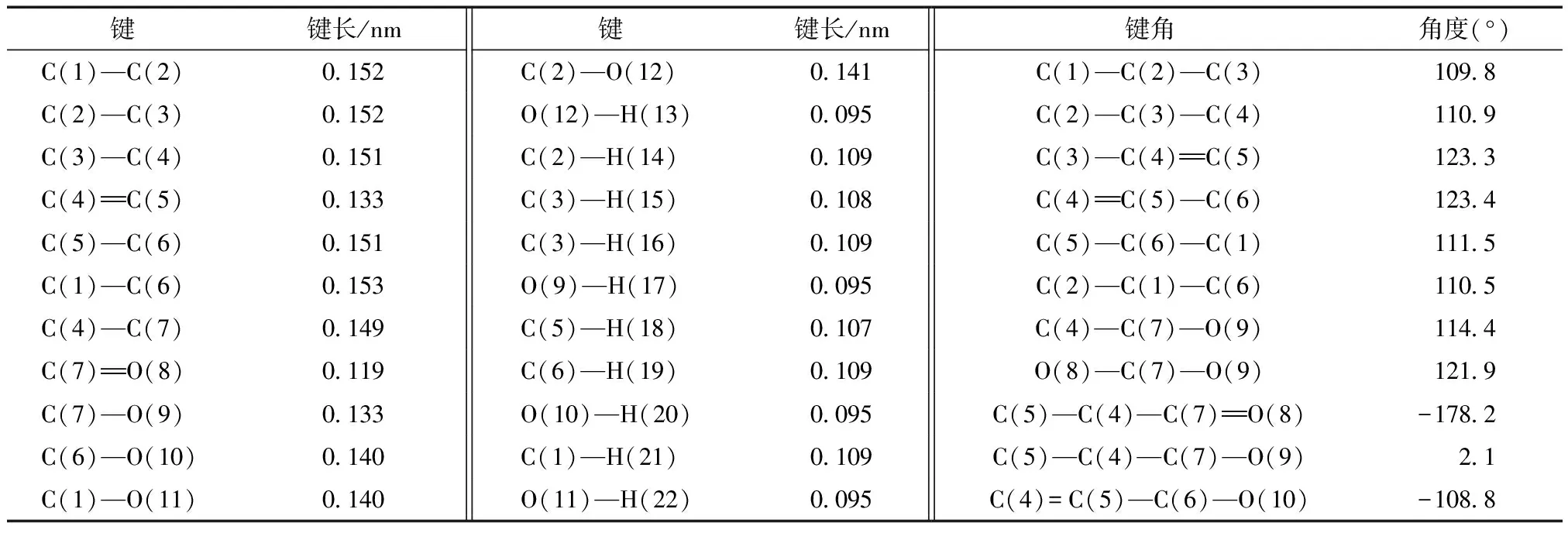
表1 分子中键长、部分键角数据

2.2 红外光谱与振动分析

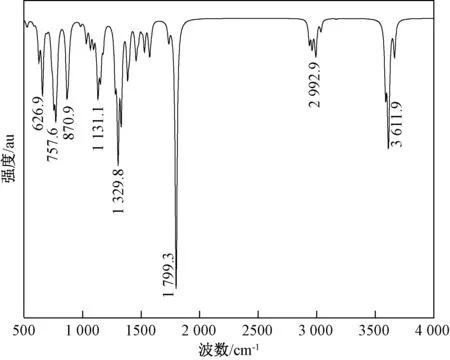
图3 莽草酸分子的红外光谱图

2.3 核磁结果分析

莽草酸分子中C、H原子核磁共振氢谱模拟计算的化学位移数值列于表2，C原子的核磁共振化学位移均比较强，主要集中在130～150 ppm区域，其中C(4)、C(11)原子的化学位移较大，这可能是因为连接的O原子的较大电负性导致；左边环中C(1)、C(2)、C(6)原子的化学位移相对最大，这也是因为碳原子连接的O原子的强电负性导致；其余C原子所处的环境基本一致，所以它们的核磁共振谱化学位移约为120 ppm. H原子的核磁共振化学位移也出现了明显的差异，其中与O原子直接相连的H原子化学位移大，而碳碳双键上的H原子的化学位移最小，这主要归因于周围环境的吸电子或供电子效应的不同. 密度泛函的计算结果，与刘富发等[34]报道的实验数据相比较，相对误差约为3.24%，这也充分说明了本研究的计算结果是较准确和可信的.

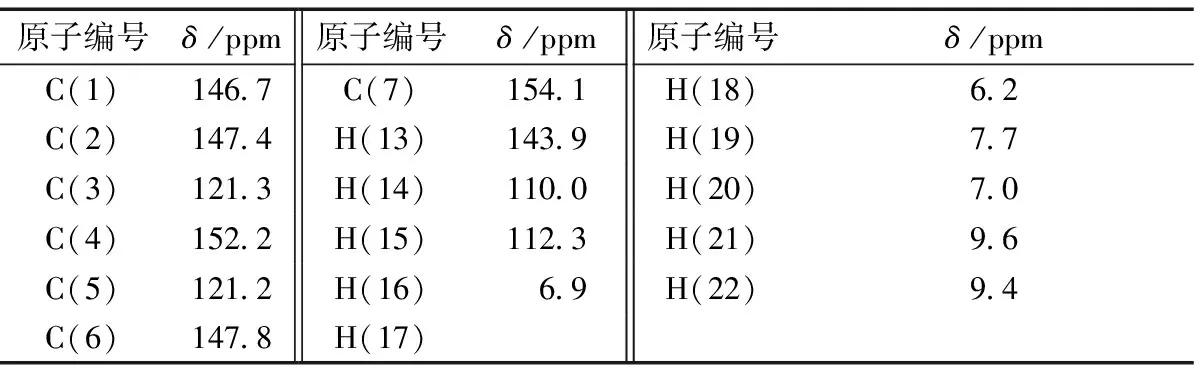
表2 莽草酸分子中C、H原子的核磁共振化学位移

注：δ化学位移.

2.4 电荷、自然轨道(NBO)分析与分子轨道

分子内原子所带的电荷多少可以推断出分子活性部位，归属于亲电或亲核部位及强弱.本研究同样适用量子化学中的密度泛函方法，在优化几何构型的同时就给出了各个原子的Mulliken电荷数值，同时NBO方法也能推测其Natural电荷数值，两者均列于表3进行对比.由表3可知：分子中带正电荷最多的为与O原子直接相连的C原子，这是由于所连的O原子强电负性缘故；分子中羧基中氧原子所带的负电荷最多，表明其部位可能作为亲电取代的活性位点；没有连O原子的C原子带有微量的负电荷，是由于周围的H原子的供电子效应所导致. 两种方法体现的整个分子中原子所带电荷分布是基本一致的，O原子带的负电荷最多，同时也反映了所计算的电荷的准确性较理想.

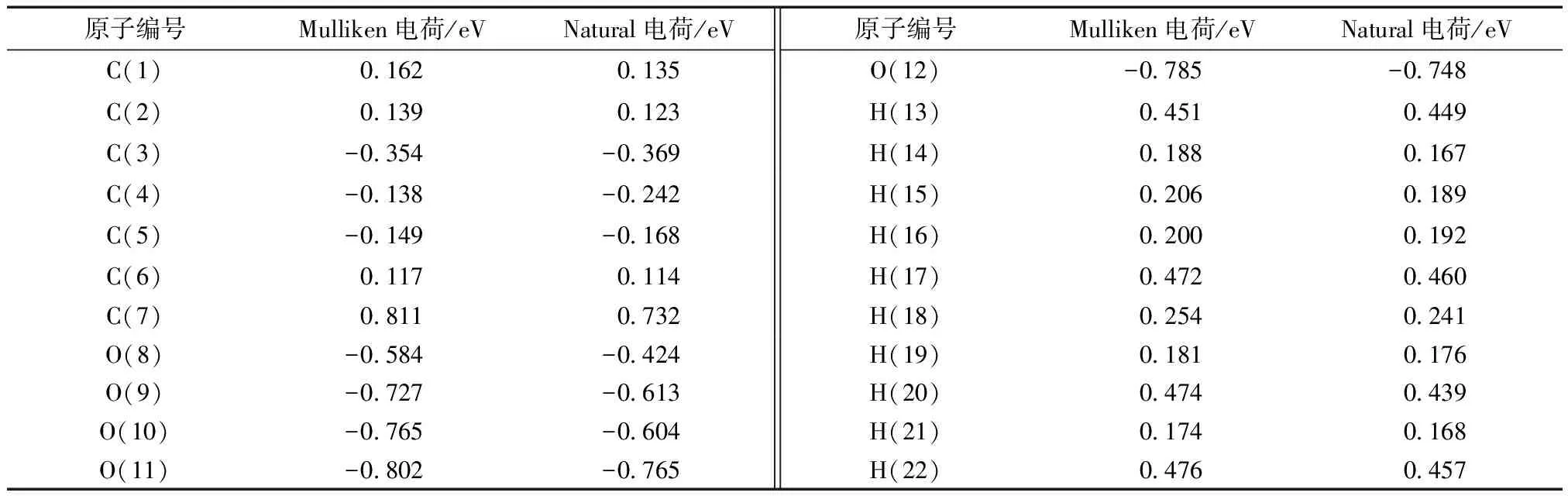
表3 莽草酸分子中各原子的Mulliken及Natural电荷

图4 分子轨道能级、电子密度、静电势图

表4 莽草酸分子中NBO分析的化学键二级微扰能

2.5 Fukui指数及药理活性分析

密度泛函活性理论(DFRT)的活性指数在无机和有机化学体系中用于判断分子的反应活性，已具备了较好的科学认可和广泛的应用. 朱尊伟等[35]曾提出Fukui函数和局域软度可应用于判断亲电加成反应的区域选择性，通过计算探究和讨论了溴苯硒与不对称苯乙烯的亲电加成反应中，Fukui函数可以很好地诠释HCl容易进攻马氏碳原子的原因.崔宝秋等[36]曾使用Fukui函数扫描蚯蚓血红蛋白活性中心，显示了蚯蚓血红蛋白的活性中心由铁离子转移到质子化的氧原子，能对其血红蛋白的载氧功能产生被抑制或减弱的特殊现象，对微观生物活性点上的分子作用机制做了较好的理论解释.Morrison[37]曾深度解读Fukui函数与波函数计算的内在联系，提出外部临界电子的效应在Fukui函数计算中是不可忽视的重要部分.宋淼[38]也曾系统地使用Fukui函数对呋喃和吡咯及其衍生物性质进行系统的理论研究，成功地预测了五元杂环化合物可能发生的亲电反应活性位点，表明计算结果与实验具有良好的匹配性.

表5 莽草酸分子的DFRT下活性指数(eV)

注：I.第一电离势；A.电子亲和势；η.化学硬度；μ.化学势；ω.亲电指数；ΔEn.亲核力差值指数；ΔEe.亲电力差值指数.

图5 Fukui指数扫描图注：f+(r).亲核Fukui函数；f-(r).亲电Fukui函数； f2(r).二次方Fukui函数.

2.6 热力学性质

分子的能量数据对分子的性质也能发挥重要的作用，本研究在相同的基组水平和方法上，利用B3LYP方法对莽草酸分子的热力学性质进行了详细的计算. 获得了不同温度在100～1 000 K范围内的标准状态下的等压比热容(Cpθ)和标准状态下的热熵变(Sθ)数值(表6)，莽草酸分子的Cpθ随温度的升高变化不大，但Sθ随温度的升高变化较大，表明分子在的热效应受温度的影响不大，但分子构型变形度受温度影响明显，这对进一步实验做了有力的理论补充.

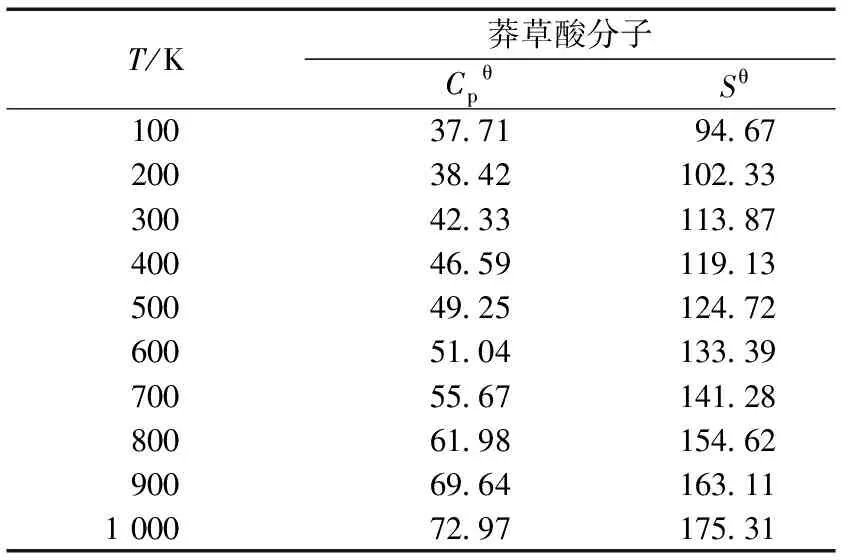
表6 不同温度的热力学性质参数

注：T.温度，k;Cpθ.标准状态下的等压比热容，J/(kg·K);Sθ.标准状态下的热熵变.

3 结 论