利用ANSYS进行压载挤淤有限元分析

孔德怡,李天文

(海军东海工程设计院,上海 200083)

1 概 述

我国东南沿海广泛分布着淤泥质软弱土,土层的含水率和灵敏度高,承载力极低,土性很差,不经处理无法用于工程建设。为了保证新建海堤、道路等设施的安全性,必须进行地基处理。常用的地基处理方法是堆载或真空预压法。但是预压法工期长,需要处理的面积大,成本较高。而海堤、道路呈条状布置,在工期要求紧张的条件下,可以选择挤淤法针对条状区域进行处理,以达到速度快成本低的效果。但是挤淤法的理论计算和实践经验较少,需要针对性研究。杨光煦[1]根据土的极限滑动平衡理论推导了挤淤公式,被《地基处理手册》引用。闫澍旺等[2]改进了理论计算假定,考虑了压载体形状和隆起部分土的影响,推导了挤淤公式并进行了室内试验。汪洪星等[3]用ABAQUS分析了大高度堆载的挤淤深度。本文尝试用ANSYS分析压载挤淤问题,并分析其与土的极限承载力的关系。

2 压载挤淤深度理论计算

2.1 常用挤淤公式

压载挤淤法的定义是依靠换填材料的自重,使软弱层遭受破坏后被强制挤出而达到置换土体改良土性的方法。根据目前的工程实践,压载挤淤法适用于厚度在10 m以内流动性大,基本无硬壳层的大面积流塑状淤泥地基处理。

根据以上定义,压载导致其下软弱土发生了剪切破坏,土体沿破坏面发生滑动。随着压载体下沉,滑动面逐渐扩展,其上的抗滑力矩也逐渐增大,再加上隆起土的自重反压作用,滑动逐渐稳定停止,土体建立了新的平衡状态。因此可以根据土的极限平衡原理计算不同压载高度对应的挤淤深度。工程中常用的计算公式如式(1)、(2)。

(1)

(2)

其中cu为淤泥层抗剪强度(kPa)；γ、γs分别为淤泥和压载体重度；b为压载体宽度；d为压载体在淤泥层中的下沉深度,即挤淤深度；H为压载体高度。计算简图见图1。

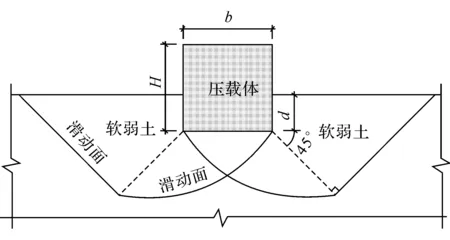
图1 压载挤淤计算简图

式(1)是《地基处理手册》给出的计算公式[1],式(2)是文献[2]的理论推导公式。比较两者发现,公式构成基本相同而具体的系数有所不同,且前者计算压载高度应大于后者。根据文献[2]的模型试验数据,式(2)与试验数据更为吻合。

2.2 土的极限承载力与压载挤淤的关系

从图1的破坏形式可以看出,如果把压载体比作是上部结构的话,则压载挤淤过程与在上部结构荷载作用基底土的破坏过程相同。也就是说,压载挤淤问题本质上就是土的极限承载力问题。这个问题已有许多专家学者进行过研究。比较经典的有斯肯普顿公式和汉森公式[4]。其中斯肯普顿公式假设基底光滑,且忽略基础底面以上两侧土的抗剪强度,而将这部分土作为分布在基础两侧的均布荷载来考虑。这部分均布荷载限制了塑性区的滑动隆起,使得地基承载力得到提高。这种假设对于浅埋基础误差不大,但是当埋深较大时就可能与实际情况差别较大。而汉森公式则通过深度系数来考虑基础底面以上两侧土的抗剪强度对承载力的提高。

为简化起见,以下分别针对饱和软黏土(φ=0°)列出土的极限承载力公式。式(3)是斯肯普顿公式,式(4)是汉森公式。

Pu=5.14c+γd

(3)

Pu=5.14dcc+γd

(4)

H=Pu/γs

(5)

其中c为饱和软黏土的粘聚力(kPa)；dc为考虑基础埋置深度的计算系数；Pu为土的极限承载力；其他与式(1)、(2)相同。根据公式(3)～(5)也能得到压载体高度H和挤淤深度d之间的关系。对比斯肯普顿公式与汉森公式,两者区别在于基础埋置深度系数,该系数一般大于1.0,则一般情况下汉森公式计算得到的压载体高度要大于斯肯普顿公式。

3 压载挤淤深度有限元计算

通过理论计算公式虽然能够得出压载挤淤深度,但是推导过程中对实际问题进行了较大简化,一般只适用于简单场地,在实际应用中具有较大的局限性。而有限元方法通过数值计算,不但可以考虑基底以上土的抗剪强度,而且可以分析如土层分布不均匀、不均匀压载等复杂场地问题,研究各个参数的敏感性,为后续工程提供数据支撑。

本文采用ANSYS有限元软件进行分析。其中土体用PLANE82平面应变单元模拟，土的本构关系采用Drucker-Prager破坏准则。但由于理论计算一般均采用摩尔-库伦破坏准则,所以为了便于比较,采用等效安全系数k将土参数进行折算[5],详见式(6)～(8)。

c′=c/k

(6)

(7)

(8)

其中φ为原始内摩擦角,c为原始粘聚力,k0为摩尔-库伦准则下的安全系数,k为Drucker-Prager破坏准则下的安全系数。令k0=1.0即可得到摩尔-库伦准则下极限状态对应Drucker-Prager破坏准则下的安全系数。

图2 模型2(与汉森公式对比)

为减少单元数目提高运算效率,取一半土体进行分析,左上角的缺口模拟压载体挤淤区域,其深度即挤淤深度,见图2。模型左侧施加对称边界条件；模型底部约束水平和竖向位移；右侧约束水平位移；缺口处竖向边界约束水平位移,用以模拟压载体对土体的约束。

为了得到某挤淤深度d对应的压载体高度H,可施加一个均布荷载Pu于挤淤区底面,采用试算法进行分析。即通过不断增大该均布荷载直至模型计算不收敛,则前一级荷载就是该挤淤深度对应的压载。根据式(5)即可得到压载体高度H。

3.1 与极限承载力理论计算公式对比

首先与理论计算公式结果进行对比,以验证有限元法分析压载挤淤问题的适用性。土的原始粘聚力取12 kPa,原始内摩擦角取0°,代入式(8),安全系数k为1.155。

与斯肯普顿解对比时,模型挤淤区深度取0,并且在右侧土体表面施加均布荷载p0,其中p0=γd,用以考虑压载体底面以上土自重的影响,模型详见图3。与汉森公式对比时,直接按图2所示模型计算,程序自动考虑压载体底面以上土的自重和抗剪强度。

图3 模型1(与斯肯普顿解对比)

图4 有限元解与斯肯普顿公式解对比

图5 有限元解与汉森公式解对比

通过图4、图5对比,有限元解与斯肯普顿公式和汉森公式计算结果误差均较小,且变化趋势相同。从整体分析,随着挤淤深度的增大,压载体高度也随之增高,且近似呈线性关系。ANSYS解比极限承载力理论公式解大。由此说明利用ANSYS有限元模型能够较好地分析压载作用下土的极限承载力问题,证明了压载挤淤问题本质上就是土的极限承载力问题，有限元计算的压载体高度偏于安全。

3.2 与挤淤公式对比

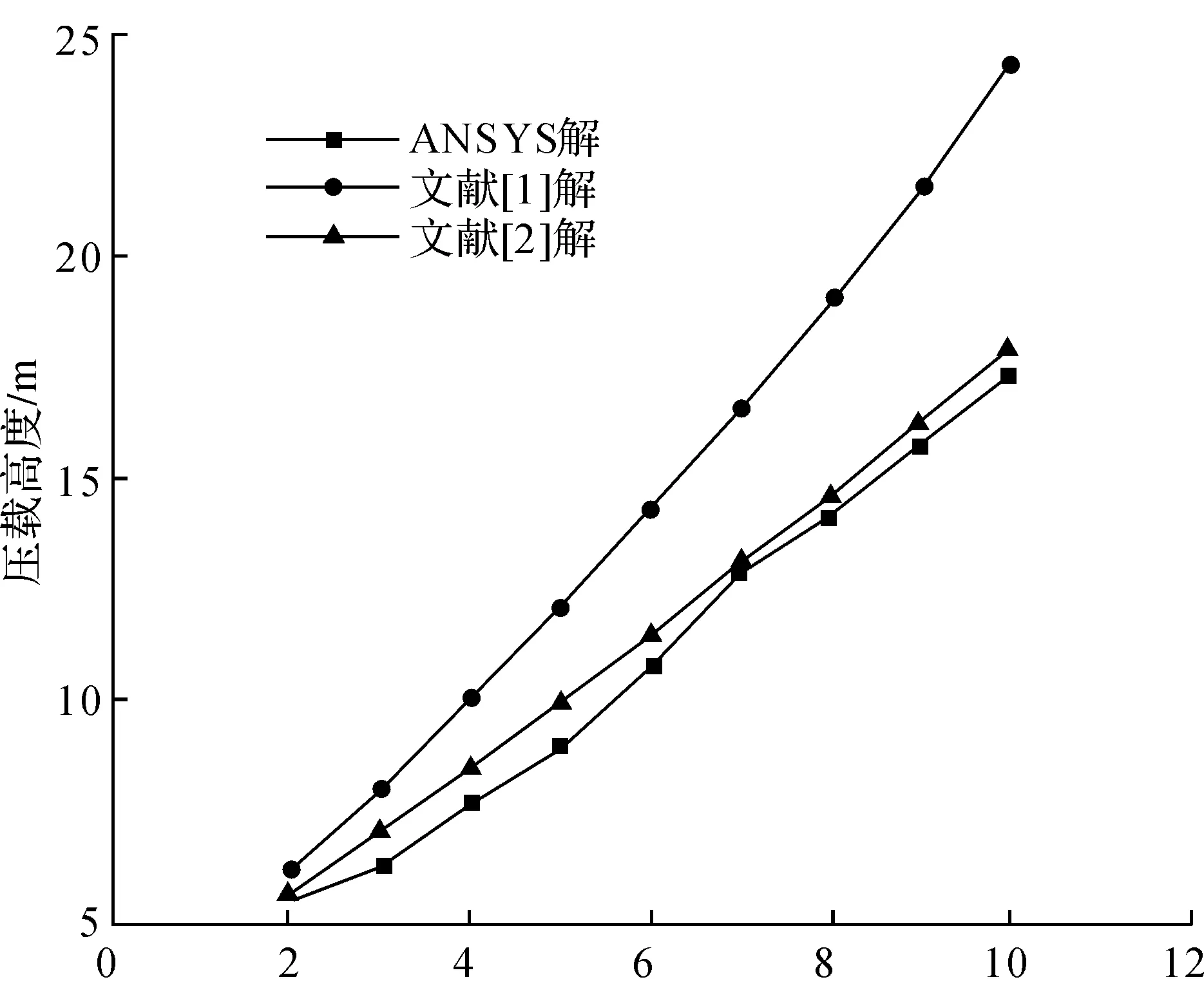
图6 有限元解与挤淤公式解对比

接下来将ANSYS解与挤淤公式(1)、(2)结果进行对比,进一步评价有限元法的适用性。考虑到淤泥被挤出后在四周隆起,该部分土的自重对挤淤效果有影响,有限元分析时将隆起部分土的自重按照三角形分布荷载加载至四周土体表面。其中隆起部分土体总重等于被挤出部分土体总重(即图2模型左上角缺口区域土体总重),分布宽度根据图1中理论滑动面范围确定。此种简化与文献[2]推导时的理论假设相同。

从图6对比可以得知,ANSYS解与文献[2]即公式(2)结果相差较小,而公式(1)解则较两者偏大。这与文献[2]的试验结果相互得到验证,进一步证明了ANSYS模型的有效性。从图7可以看出,在土体即将破坏时,内部塑性区分布与图1假设滑动面相似,但是弧形滑动面比图1长,且并不是严格的面滑动,而是相邻区域进入了塑性；土体表面出现了明显的隆起现象,与工程实际现象吻合。

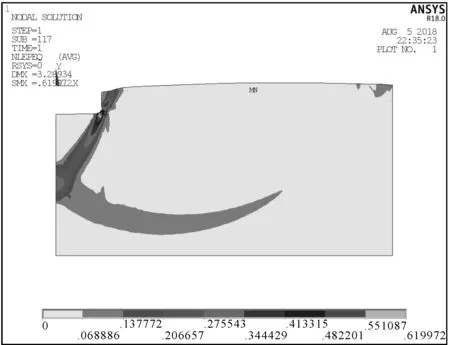
图7 土体滑动破坏时的塑性应变云图

3.3 双层地基挤淤分析

以上均针对均匀软土进行分析,但是实际工程场地通常分布着双层土,一般来说上软下硬。接下来利用ANSYS有限元模型分析上软下硬双层地基条件下的挤淤情况。其中上层仍为饱和软黏土,参数与前文算例相同，下层为硬质黏土,粘聚力为15 kPa,内摩擦角12°。以2 m挤淤深度模型为例进行分析。

图8 不同软土深度对应的压载体高度(d=2 m)

图9 软土深度10 m时塑性云图(d=2 m)

图10 软土深度20 m时塑性云图(d=2 m)

从图8可以得出,随着软土深度增大,压载体高度先是迅速减小,然后逐渐增大,最终稳定至均匀软土计算值附近。根据图9可知,当软土深度很小时,由于下层硬质土的直接支撑作用,上部荷载直接传导至下部硬质土,因此需要较大的压载才能使软土破坏,且此时的破坏模式与图1完全不同。根据图10、图11可知,随着软土深度的增大,逐步过渡到图1所示的破坏模式。当硬质土层在滑动面范围内时,软土在软硬接触面形成应力集中导致破坏,此时所需的压载较小；随着硬质土层埋深的增加,最终过渡到图1的完整滑动破坏模式,此时的压载体高度与前文分析结果以及式(1)、(2)相近。

在实际工程中,压载挤淤常在淤泥深度小于10 m 的场地条件下采用,与图9所示情况类似。因此可以推断,在上软下硬土层场地,且软土厚度不大的情况下,所需压载体高度较理论计算值大,即应超载挤淤。根据以上算例,至少超载20%。

图11 软土深度50 m时塑性云图(d=2 m)

4 结 语

通过比较土的破坏模式,可以得到以下结论：

1)压载挤淤问题与土的极限承载力问题本质上都是软弱土层在外荷载作用下发生剪切破坏,土体沿破坏面滑动,顶面隆起的过程。

2)文献[1]提出的压载高度计算工程偏大,文献[2]提出的计算公式与有限元计算、室内试验数据吻合较好。

3)利用ANSYS可以较好地模拟土在外荷载作用下发生破坏的过程,可以用来分析土的极限承载力及压载挤淤问题。

4)通过分析软硬双层地基的挤淤问题可以推断,常见的薄层软土挤淤需要更重的压载体才能保证较好的挤淤效果。