基于结构自适应的神经网络预测NBA比赛结果

卞 捷

（美国亚利桑那大学，亚利桑那州 AZ85621）

1 引言

1.1 NBA和比赛预测

美国职业篮球联赛（NBA）是全美最大的男子篮球职业联赛，它吸引了30支球队和全世界最出色篮球运动员来争夺冠军。NBA在美国非常流行，许多媒体比如ESPN和TNT会对NBA每场比赛进行转播。NBA这项联赛每年不仅能从球票贩卖、赞助活动已经电视转播版权这些方面获得巨大的商业利益，还衍生出巨大的比赛博彩市场，而博彩市场的发展又高度依赖于赛前准确的比赛结果预测[1]。

幸运的是，有很多预测比赛结果的方法，本文使用BP神经网络来模拟比赛双方的特征与比赛结果的映射函数。考虑到采用不同的ANN结构会得出不同的测试误差和复杂度，本文致力于寻找一种某种程度上最优化预测准确率的BP神经网络。

1.2 人工神经网络中训练、测试和训练次数关系曲线

如图1所示，随着训练次数的增长，训练误差会相应递减，但是测试误差会随之先递增再递增。所以，在测试误差到达其所在极小点之前，训练误差和测试误差都随着训练次数的增长而减小；在测试误差曲线到达其所在极小点后，训练误差曲线下降的同时测试误差曲线随训练次数上升。因此，我们需要将训练次数确定在测试误差曲线到达极小点的位置。

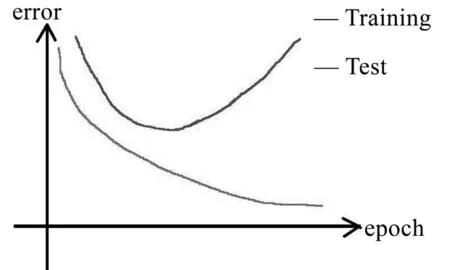
图1 人工神经网络中训练、测试和训练次数关系曲线

2 实现步骤

2.1 准备数据集

文中数据集从NBA官网获取，数据分别存放在两个txt文件“gameresultofFEB.txt”和 “teamperformanceofJAN”中。“gameresultofFEB.txt”中记录了NBA 2016—2017常规赛季二月份每场比赛的比赛数据，包含了每场比赛的对阵球队名、比赛最终得分以及用逻辑变量代表的比赛胜负关系（取1代表球队1获胜，取0代表球队2获胜）。“teamperformanceofJAN.txt”中则记录了NBA每支球队在2016—2017常规赛季1月份的所有比赛的平均表现，其中包含了许多球队特征比如比赛胜率、三分球命中数、篮板球数等。

收集完这些数据后，通过编程生成适合输入人工神经网络的数据集，数据集中的每个数据点由第一个球队的特征信息、第二个球队的特征信息以及比赛历史记录的胜负结果（1代表第一个球队获胜，0则代表第一个球队告负）组成[2]。

2.2 利用结构自适应的人工神经网络预测比赛结果

在准备好数据集后，将它划分成两部分：前100个样本数据用作训练集，剩下的65个样本数据作为测试集。这样划分的根据是因为数据集是由时间顺序排列的，在进行预测的时候，我们总是使用过去的数据来对未来的结果进行预测，毕竟，我们不能使用未来的数据来预测过去的比赛结果。然后，考虑到结构的简洁和效率，我们这里将隐含层的个数设置为2个（通常情况下，我们将隐含层个数设置为1～3个）。

在将隐含层个数确定为2之后，剩下来BP神经网络的具体结构由每个隐含层节点分配个数确定。本文先将训练迭代次数设置为500（因为对于文中使用的数据集的大小，500训练迭代次数不会引起过度拟合），然后我们将第一个隐含层节点个数和第二个隐含层节点个数（i,j）设置为i=5,10,15,...,75和j=5,10,15,...75的各种组合，对各种（i,j）组合的人工神经网络结构进行训练并且测试结果，最终再选取其中测试误差最小所对应的（i,j）结构来作为最理想的BP神经网络结构，某种程度上这相当于一种限制深度的greedybest搜索。

在确定好ANN的结构后，通过对一系列不同训练迭代次数的测试，我们可以寻找到最接近测试误差曲线极小点的节点位置，这个节点既不会带来过拟合也不会带来欠拟合，并且是所找到的对应最小的测试误差位置。这里所对应的测试误差将会作为文中结构自适应神经网络最终的测试误差[3]。

2.3 实验结果与结论

训练迭代次数为500时各种隐含层可能结构的测试误差情况如表1所示。

表1 训练迭代次数为500时各种隐含层可能结构的测试误差情况

这里我们选取表格中最小的测试误差位置作为所确定的隐含层结构，最终确定的隐含层结构是第一个隐含层节点个数为70，第二个隐含层节点个数为20（考虑到简洁性，文中以节点个数5为间隔枚举，如图2所示）。

图2 隐含层结构及节点

根据图3确定本文所使用的结构自适应的BP神经网络的测试误差为0.338 5（epoches=2 600）。

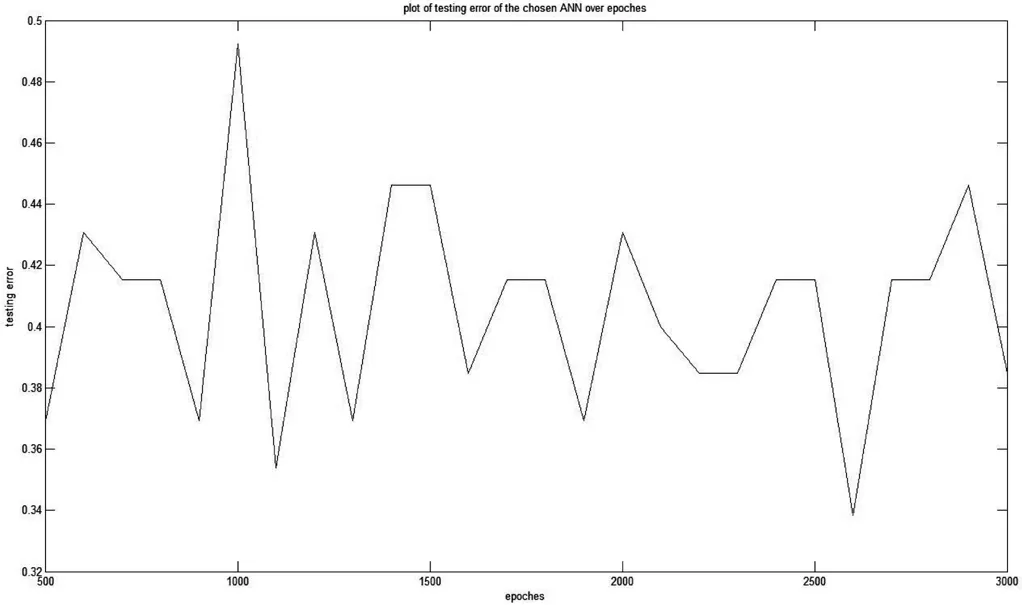
图3 不同训练迭代次数下此神经网络的测试误差分布

为了说明70-20的隐含层结构是最优的，我们还对其他一些接近70-20的隐含层结构（比如70-25，75-20）进行测试。

根据图4确定在70-25的隐含层结构下测试最小误差为0.369 2。

根据图5确定在70-15的隐含层结构下测试最小误差为0.338 5。

根据图6最终的测试误差为0.353 8。

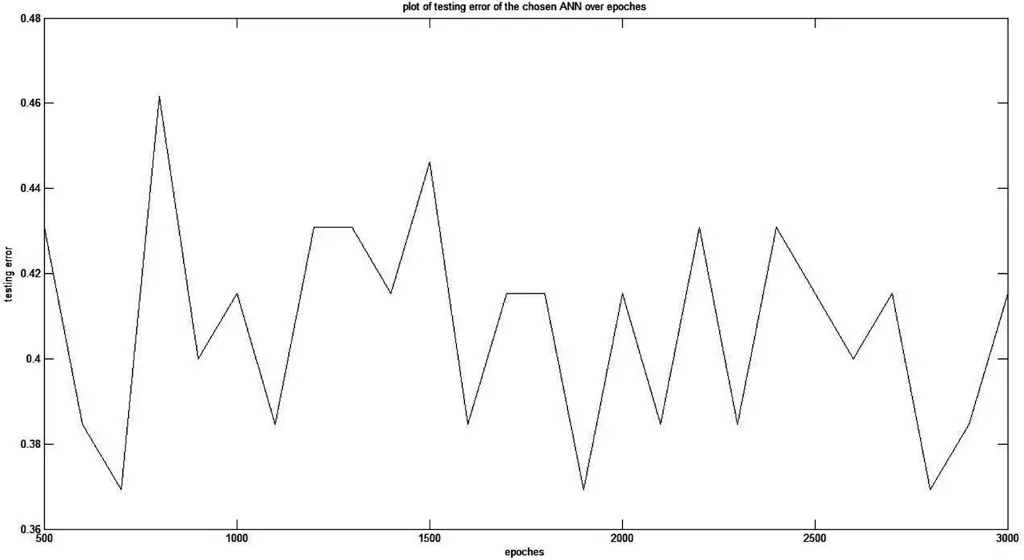
图4 当隐含层结构为70-25的测试误差与训练迭代次数分布

图5 当隐含层结构为70-15的测试误差与训练迭代次数分布

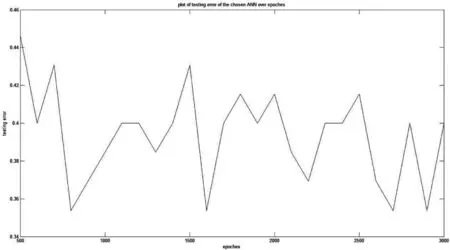
图6 当隐含层结构为65-20时的测试误差分布

根据图7，此结构的测试误差为 0.338 5。

从表2可看出，我们从训练次数500次（考虑到训练集大小500次不会带来过拟合）根据最小化测试误差所选择的70-20隐含层结构的测试误差也是它相邻结构的最小测试误差。因此证明本文中的方法可以寻找到BP神经网络的局部最优结构，有时候甚至是全局最优结构。

表2 各隐含层结构测试误差汇总

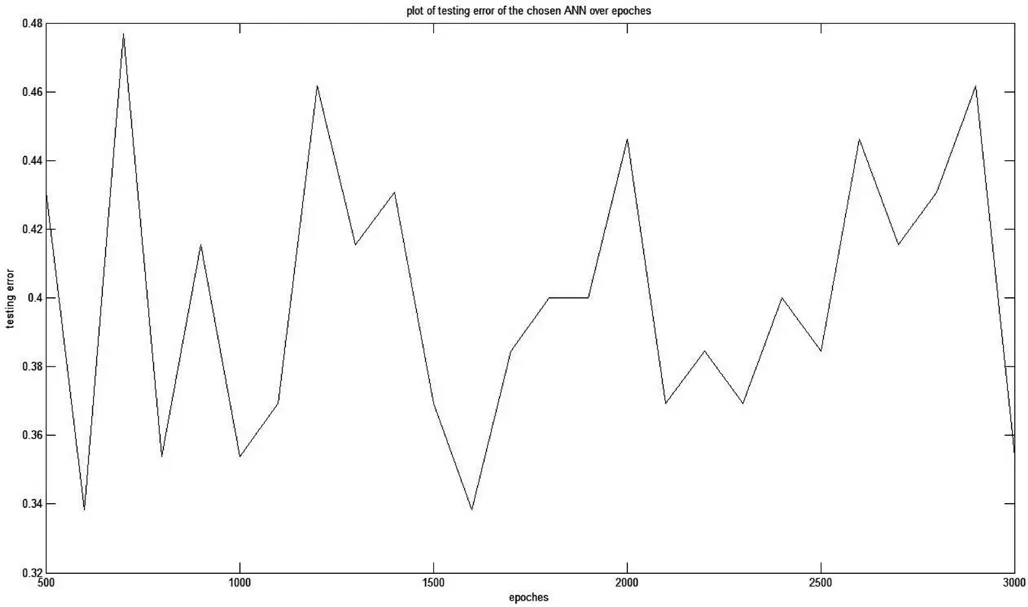
图7 当隐含层结构为75-20时的测试误差分布

通过应用文中的结构自适应的BP神经网络，我们将NBA比赛胜负结果的预测准确率提高到了66.15%。我们先将训练迭代次数定为一个不会带来过拟合的次数，然后计算不同隐含层结构下的测试误差，通过最小化测试误差，我们选择最小测试误差所对应的结构作为理想的隐含层结构。在找到此种结构之后，对此结构在不同训练迭代次数下的测试误差进行计算，这一过程的必要性在于随着训练迭代次数的增加，人工神经网络预测会发生欠拟合和过拟合现象，而我们所需要的是介于欠拟合和过拟合之间的那部分。之后通过与相邻隐含层结构人工神经网络之间的比较，我们发现本文所提出的理想隐含层结构确实是在局部最理想的人工神经网络结构[4]。

3 有待改进的部分

（1）数据集中数据的特征量众多，其中一些特征可能与我们的预测结果无关，所以有选择地忽略其中某些量可能提高本文方法最后的预测准确率。

（2）现实世界中的数据比如本文使用的NBA比赛数据存在噪声，所以在确定理想的人工神经网络结构时可以使用一些方法比如加权投票来减弱噪声带来的影响。

（3）输入数据与预测结果之间的映射函数依赖于马尔科夫过程，这意味着我们的预测结果主要依赖于最近时间的输入数据，所以本文的预测结果可以通过增加更多最近时间的输入数据来提高预测正确率。