基于点云切片技术的曲面拟合方法研究

张开源，郑德华，张崇军

（1.河海大学 地球科学与工程学院，江苏 南京 211100）

三维激光扫描仪是以“面”的测量手段采集点云数据，由于其具有测量精度高、工作速度快、采集信息量大等诸多优点，故而又被称为“实景复制技术”[1]。该技术能实现迅速、海量获取三维点云，是测绘领域的一大创新[2]。

三维激光扫描数据处理的结果是通过进行物体表面曲面拟合来建立三维模型。由于获取的点云是海量数据以及目标物体的形态具有多样性等特点，使得对该类数据处理难度变大。现有的大部分点云曲面拟合方法拟合得到的结果能够保留一部分甚至绝大部分的原始点云特征，但有时也会出现局部失真的情况，尤其是对于复杂曲面，从而造成拟合结果精确性不高，影响拟合的效果。此外大部分点云曲面拟合方法的时间复杂度较高，拟合效率较低，尤其是针对包含多种曲面特征的复杂区域，拟合效率更低。为了能够有效地对点云数据进行处理，引入了数据分割方法。数据分割[3]不仅实现了对点云的分块和合并处理，而且建立了点云数据间的拓扑结构，为后续整体点云进行分块曲面拟合提供了便利。

本文首先引入切片方法来对点云数据进行曲面拟合，切片方法通过投影将点云数据实现降维处理，可以克服曲率和法矢变化带来的部分影响。通过切片处理，将整体点云数据分割成适量切片，能克服复杂曲面的不利影响。然后对基于切片的点云曲面拟合方法进行改进，从多个方向上对切片后的点云进行处理，得到点云拟合区域的拟合数据。为提高整体点云的光滑性，可使用基于移动最小二乘的方法对拟合后数据实现整体光滑处理。该方法保证了点云曲面拟合的质量，保留了更多的原始点云特征，可有效提高点云曲面拟合的精确性。

1 基于切片技术的点云曲面拟合方法

基于切片的点云曲面拟合方法可以分为两步：切片数据的获取及投影拟合。对切片数据的获取，分别采用定宽和自适应切片两种方法来对点云数据进行处理。对切片的投影拟合，引入移动最小二乘方法来提高切片的拟合精度。同时，提出使用双向切片法来提升点云曲面拟合的稳定性和可靠性。

1.1 点云切片宽度

在点云数据中，以某一指定方向为法方向，沿该方向设置一个平面族Γ，则某一平面E的表面线即为该平面处的点云切片，其本质为平面E和点云相交后得到的点云区域。在实际应用中，由于各种因素的影响，要严格以平面上的点来计算获取该平面处的点云切片是无法实现的，因此引入“切片宽度”，即将该平面E沿着法方向的两侧各移动相等宽度，生成两个新的平面El和Er，则两个新的平面El和Er中间的点云即为该平面所在的点云切片。点云切片宽度的确定是基于切片的点云曲面拟合方法研究的关键步骤之一，主要可以分为两大类：定宽切片宽度的确定和自适应切片宽度的确定。

1.1.1 定宽切片宽度的确定

定宽切片是比较常见的切片获取方法，它是通过计算获得切片的宽度，以此宽度为基准对点云数据进行切片处理，获得许多宽度相等的切片。目前常用的切片宽度计算方法为密度法，通过计算得出点云的密度，然后确定切片的宽度。本文介绍基于空间格网划分的密度法[4-5]，这种方法是以K邻点搜索中的空间分块策略方法为基础的[6]。根据划分好的空间包围盒网格，统计网格中空的包围盒个数来进行计算：

式中，Vt为所有小包围盒的个数；Ve为所有空的小包围盒的个数；K为邻近点的个数；n为点云的总数。

根据公式求解点云数据密度，进一步求解切片宽度：

式中，k1为经验系数，一般取值4～8。

1.1.2 自适应切片宽度的确定

定宽切片处理得到的切片宽度是一样的，适用于曲率变化小的平缓点云或平面点云。对于曲率变化较大或局部密度不均匀的区域，如果仍使用定宽切片的处理方法，得到的切片进行投影之后，就会出现厚度相差较大的情况，会对后续拟合产生重大影响，进一步影响到点云曲面的拟合。因此，本节引入一种自适应的切片获取方法，通过对切片投影厚度的控制，来调节切片的宽度，得到宽度不等的点云切片数据。自适应切片方法的主要思想是：

1）首先确定自适应处理过程中一些基本变量，例如以沿X轴为切片方向，则取最小值和最大值Xmin、Xmax作为切片的起止点。设切片的初始宽度为ΔX，这个初始宽度可以通过密度法计算得到。

2）在X1=Xmin时作为第一个切片平面，根据计算得到切片的初始宽度△X，则在X2=X1+ΔX时取第二个切片平面，两个平面之间的数据即为第一个切片数据。

3）将第一个切片数据投影到切片平面上，得到切片投影数据，判断切片投影数据的最大厚度是否超过设定的阈值。若超过设定的阈值，则进入到步骤（4）；若没有超过，则进入到步骤（5）。

5）比较X2是否超过Xmax，如果超过Xmax，则令X2=Xmax，进入步骤（6）；如果没有超过Xmax，则令X1=X2，X2=X1+ΔX，重复步骤（3）中的操作。

6）提取切片数据，处理完成。

1.2 切片拟合

点云切片数据的投影拟合是基于切片的点云曲面拟合方法的另一个关键步骤，根据切片处理方法得到点云的切片数据，对切片数据进行投影处理，然后拟合投影数据。本文引入了移动最小二乘法[7-9]（moving least square，简称MLS）来对切片的投影数据进行拟合。首先求出切片数据中每个数据点的紧支撑域，选取合适的权函数和基函数后，根据相应公式即可求出拟合后的数据。基于MLS法的拟合方法，通过选取不阶基函数和权函数得到不同的精度和光滑度，能够在一定程度上克服最小二乘法适用于数据量不大、切片形状简单的情况，但对于线形复杂、数据量较大的切片数据，则需要进行分块拟合。

1.3 基于双向切片技术的曲面拟合

在利用切片技术进行曲面拟合时，单一方向的切片方法能在一定程度上满足点云数据曲面拟合的需要。大量的实验表明，不同方向的切片得到的拟合数据效果不同。在对实验对象做切片处理时，求出的最佳切片方向仅仅是针对某一部分数据而言，不存在对所有点云数据的切片效果都最佳的切片方向。

由于不同方向切片的拟合效果具有差异性，不同方向的切片拟合效果具有不稳定性，对多个方向进行切片得到的切片数据具有一定的优势互补性。本文提出使用一种基于双向切片优势互补的点云曲面拟合方法，通过在多个方向上对同一实验对象做切片处理，得到不同方向的拟合数据。为避免拟合数据过多而造成误差累积，选取其中拟合效果最好或具有优势互补效果的两个方向的数据，然后根据移动最小二乘法原理，采用稳健光滑方法对两个方向的拟合数据进行去噪光滑处理，可得到最终的拟合数据。具体算法流程如下：

1）对待拟合点云数据进行多方向切片拟合处理，根据条件选择其中拟合效果最好或具有优势互补的两个方向切片数据，使用移动最小二乘法进行整合处理；

2）将原始点云数据和整合后的点云数据进行比较和计算，得出拟合后点云数据中每个数据点的残差Vi以及中误差σ；

4）利用剩下的点重新计算，循环执行（2）～（3）环节，直至所有点的误差都在要求范围内为止；

5）利用移动最小二乘法对最终得到的点云数据再次进行光顺处理，即可得到最佳拟合结果。

相比于最小二乘法而言，移动最小二乘法的拟合函数构造相对简单，由于引入紧支撑域，能有效提高拟合数据的光滑度，且稳健过程能有效剔除拟合过程中产生的粗差，保证了最终的拟合精度。

2 实验案例及分析

使用Trimble GX型号三维激光扫描仪对石质雕像进行测量，得到点云数据，对预处理过的数据进行分割，获得石质雕像的点云数据。由于雕像表面凹凸不平，毫无规则，所以选取整块雕像点云数据进行实验和选取部分雕像点云数据进行实验效果类似，为方便后续的实验对比，在聚类分割后的某一区域中截取一部分具有代表性的点云数据进行实验。

截取点云及其附近数据共5 768个，然后提取点云数据的外边界数据步骤为：①取K值为30，进行K邻点搜索；②计算数据点的法矢，并对其做方向一致性调整；③根据点云数据边界探测度量原则探测点云数据的边界点；④使用旋向法对点云数据的外边界进行提取，得到点云数据的外边界数据。

对点云数据使用三次多项式拟合方法做拟合处理，得到函数为：

根据曲面函数对点云曲面数据及其附近数据进行内插计算得到插值数据，再根据边界数据对点云曲面拟合数据进行提取，得到拟合数据共2 479个（见图 1）。

使用基于切片的点云曲面拟合方法对点云曲面进行拟合，主要有定宽切片方法和自适应切片方法。使用基于自适应切片（X方向）的点云曲面拟合方法对点云数据进行切片、拟合处理得到切片拟合数据，得到33条切片数据、拟合数据5 380个（见图2）。使用密度法计算得到点云定宽切片的宽度为12.5 mm，使用基于定宽切片（X方向）的点云曲面拟合方法对点云数据进行切片、拟合处理得到切片拟合数据，得到48条切片数据、拟合数据2 357个（见图3）。

基于双向切片优势互补的曲面拟合方法，在多个方向上对同一实验对象实现切片化，选取其中优势互补的两个方向（本实验使用X、Y轴两个方向进行处理）上的数据，使用稳健移动最小二乘方法进行综合处理，得到最终的拟合数据共8 736个（见图4）。

图1 基于多项式方法的点云曲面拟合效果图

图2 基于自适应(X方向)切片的点云曲面拟合效果图

图3 基于定宽(X方向)切片的点云曲面拟合效果图

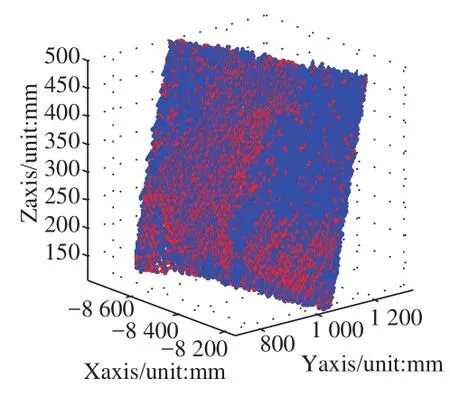
图4 基于双向切片优势互补的点云曲面拟合效果图

将本文使用的点云曲面拟合方法所得到的拟合效果进行整理，以使用最普遍的多项式曲面拟合方法为参照对象，将其他方法得出的结果与其比较，计算各方法提升的精度百分比（见表1）。

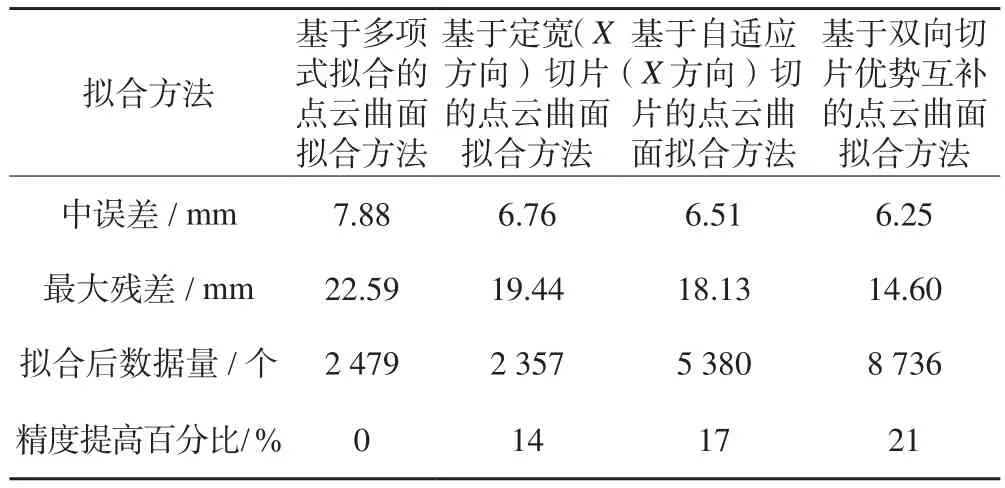
表1 不同点云曲面拟合方法拟合效果对比表

以散乱无规则、表面凹凸不平且分布不均匀的点云数据进行实验，从以上各种方法的效果图可以看出，这些方法的拟合数据能够覆盖原始点云曲面区域，满足点云曲面拟合的要求，根据实验得到如下结论：

1）对比不同点云曲面拟合方法的拟合效果，面对表面情况复杂、密度不均匀的点云，非切片法曲面拟合效果一般，切片法拟合效果明显优于非切片法拟合效果，非切片方法法拟合的中误差在6.99～7.88 mm，最大残差在21.26～22.59 mm。切片方法拟合的中误差在6.25～6.76 mm，最大残差在14.60～19.44mm。由拟合的效果可以看出，对含有多种曲面特征的点云曲面数据进行拟合，基于切片的点云曲面拟合方法优于其他方法。

2）基于定宽（X方向）切片拟合的中误差为6.76 mm，最大残差为19.44 mm。基于自适应（X方向）切片拟合的中误差为6.51 mm，最大残差为18.13 mm。自适应切片能够根据点云曲率和厚度的变化合理地进行切片处理，由拟合的效果可以看出基于自适应切片的方法优于基于定宽切片的方法。

3）基于双向切片优势互补的拟合方法的中误差为6.25 mm，最大残差为14.60 mm。使用单向切片方法对点云曲面拟合的效果具有不稳定性，因此本文提出使用双向切片优势互补的方法来提高点云曲面拟合的稳定性。由拟合的效果、拟合后数据量及精度提升百分比可以看出，基于双向切片优势互补的点云曲面拟合方法明显优于单向切片方法。

3 结 语

使用单向的点云切片方法能够快速、高效地对点云曲面数据进行拟合，由于切片方向不是唯一的，造成点云曲面拟合效果存在不稳定性。本文提出了一种基于双向切片优势互补的点云曲面拟合方法，选择拟合效果最好或具有优势互补效果的两个方向的数据，利用移动最小二乘方法进行稳健光滑处理来获得最终的拟合数据。根据实验结果分析，相对于多项式拟合方法、单向切片方法，基于双向切片优势互补的点云曲面拟合方法在精度和稳定性方面均有了明显提升。但本文主要对双向切片方法进行了研究，在今后的工作中，可以进行深入研究一种基于三维空间特征方向或者更多方向的切片方法来提高点云曲面拟合结果的稳定性和可靠性。