Some Geometric Invariants of Pseudo-Spherical Evolutes in the Hyperbolic 3-Space

H.S.Abdel-Aziz ,M.Khalifa Saad, and A.A.Abdel-Salam

1 Mathematics Department,Faculty of Science,Sohag University,82524,Sohag,Egypt.

2 Mathematics Department,Faculty of Science,Islamic University of Madinah,170 El-Madinah,ΚSA.

Abstract:In this paper,we study the pseudo-spherical evolutes of curves in three dimensional hyperbolic space.We use techniques from singularity theory to investigate the singularities of pseudo-spherical evolutes and establish some relationships between singularities of these curves and geometric invariants of curves under the action of the Lorentz group.Besides,we defray with illustration some computational examples in support our main results.

Keywords:Pseudo-spherical evolutes,evolute curves,hyperbolic 3-space.

1 Introduction

The study of the extrinsic differential geometry of submanifolds in hyperbolic space is of special interest in relativity theory.On the other hand,the evolute of a space curve in Euclidean differential geometry is defined to be the locus of the center of osculating circles of the curve.The principal tools for the study of evolutes are the Frenet-Serret formulae and the distance squared functions on curves.In our case,we adopt a special pseudoorthogonal frame in H+3(-1).We also define hyperbolic height functions on hyperbolic space curves.With the aid of a bit of singularity theory of hyperbolic height functions,we study singularities of evolutes and establish the relation between these singularities and hyperbolic invariants of the original curve.Torii studied other objects related to hyperbolic plane curves by using a similar framework and method as used [Torii(1999)].Here,for convenience,we concentrate only on the hyperbolic evolutes of space curves.Similar descriptions for Euclidean plane curves are found in Bruce et al.[Bruce and Giblin(1992)].

For a curve γ ∈ H+3⊂E14,we choose the unit tangent vector field T(s)and another normal vector fields E1(s)and E2(s)along γ(s).As a result,we construct a pseudoorthonormal frame { γ(s),T(s),E1(s),E2(s)}along the curveγ.Also,we define two families of functions on a curve which are a timelike height function HTand a spacelike height function HS.Differentiating these functions,we obtain two new invariants σHand,whose properties are characterized by some conditions of derivation of HTand HS.

For instance,

if and only if σH=0and some other conditions [Bruce and Giblin(1992)].

Consider the surface M = H+3(-1),in this case,we define two important curves; hγin the hyperbolic space and dγin de Sitter space by observing the conditions of first and second derivation of HTand HS,respectively.We callhγ,a hyperbolic evolute of γrelative to Manddγ,a de Sitter evolute of γrelative toM.We show that the hyperbolic evolute hγis constant if and only if σH=0.In this case,the curve γis a special curve on the surfaceM,which is called a hyperbolic-slice(or an H-slice)of M.Also,we show that the de Sitter evolute dγis constant if and only if σD=0and define a special curve on the surface Mcalled a de Sitter-slice(or a D-slice)ofM .We consider H-slice and D-slice of M which is the model curves on the surface M[Sato(2012)].As an application of the theory of unfolding of functions,we give a classification of singularities of both the hyperbolic evolute and the de Sitter evolute in Theorem 4.2,which is one of the main results of this work.

The curves and their frames play an important role in differential geometry and in many branches of Science such as Mechanics and Physics,so we are interested here in studying one of these curves which has many applications in Computer Aided Design(CAD),Computer Aided Geometric Design(CAGD)and mathematical modeling.Also,these curves can be used in the discrete model and equivalent model which are usually adopted for the design and mechanical analysis of grid structures.So,we are looking forward to see that our results will be helpful to the researchers who are specialized in this field.

2 Basic concepts

In this section,we introduce some definitions and basic facts which are needed in the subsequent sections(for more details see [Izumiya,Pei and Torii(2004); Liu(2014)]).

Let R4denotes the four-dimensional vector space.For any

We call(R4,〈,〉),the Minkowski 4-space and denoted by E14.We say that a vector x∈E14is spacelike,lightlike or timelike if 〈 x1,x2〉＞0,〈x1,x2〉=0or〈x1,x2〉＜0,respectively.The norm of the vector x ∈E14is definedFor a nonzero vector υ ∈E14and a real numberc ,we define a space with pseudo normal υby S(υ,c)={x∈E14|〈x,υ〉=c}.

We call S(υ,c)a spacelike space,a timelike space or a lightlike space if υis timelike,spacelike or lightlike,respectively.

Now,we define a hyperbolic space by

and de Sitter 3-space by

For any x=(x1,x2,x3,x4),y =(y1,y2,y3,y4)andz=(z1,z2,z3,z4)∈E14,the pseudo vector product of x,y and z is defined as follows:

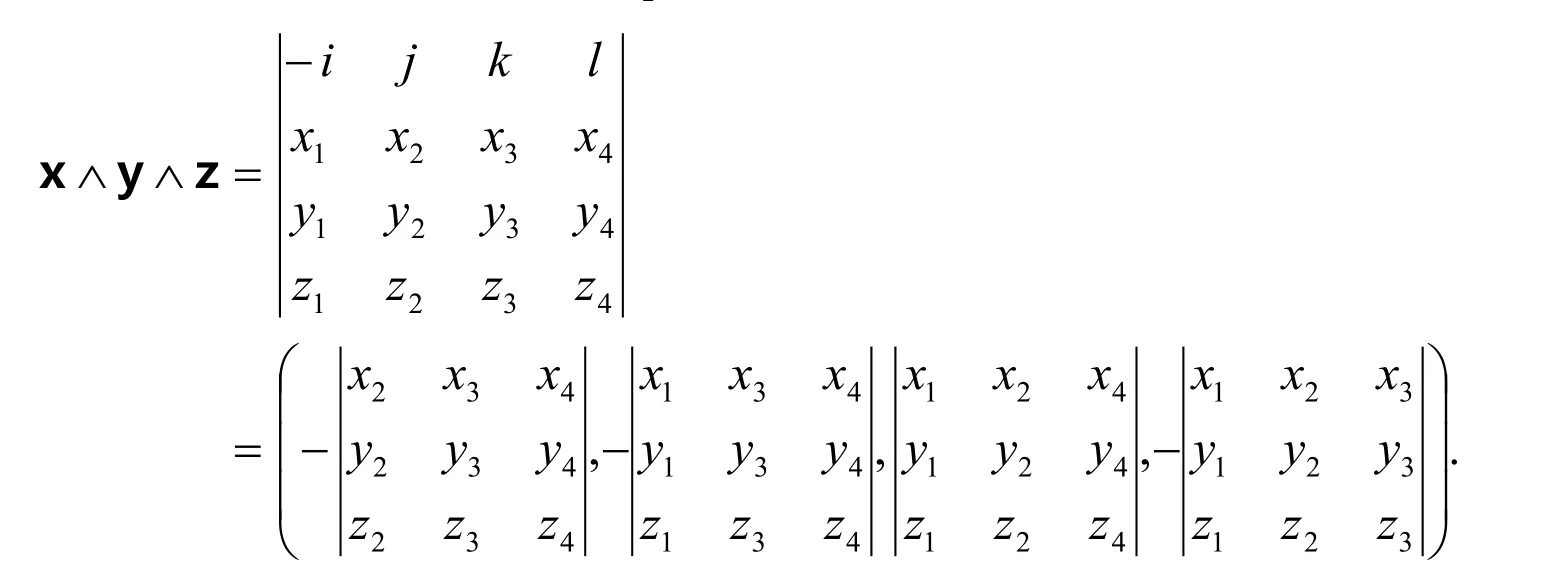
We now prepare some basic facts of curves in hyperbolic 3-space.

Let γ:I → H+3⊂E14;γ(t)=(x1(t),x2(t),x3(t),x4(t))be a smooth regular curve in H+3for any t ∈Iwhere Iis an open interval.

Here,we construct the explicit differential geometry on curves in H+3(-1).

Let γ:I → H+3(-1)be a regular curve.Since H+3(-1)is a Riemannian manifold,then we can reparameterize γby the arc-length.Hence,we may assume that γ(s)is a unit speed curve.So,we have the tangent vector T(s)=γ′(s)with

Moreover,define E2(s)=γ(s)˄T(s)˄E1(s),we have a pseudo orthonormal frame{γ(s),T(s),E1(s),E2(s)}of E14alongγ.By standard arguments,under the assumption thatT′(s),T′(s)≠-1,we have the following Frenet formulae:

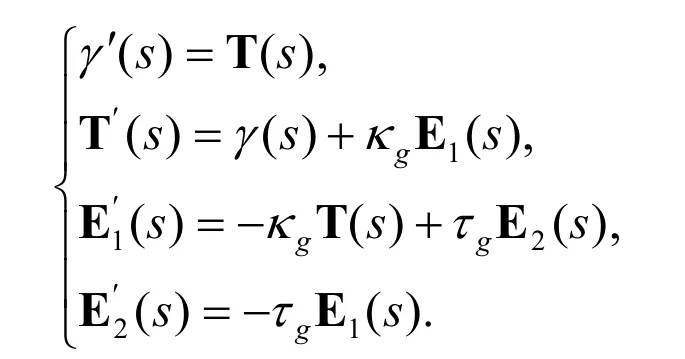
or in the matrix form:

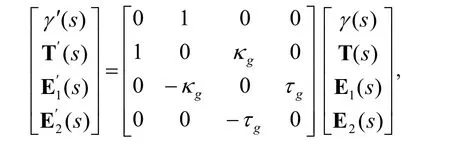
where

are the geodesic curvature and geodesic torsion of the curve γin H+3(-1),respectively(see [Liu(2014)]).

Since

therefore,the condition T′(s),T′(s)≠-1is equivalent to the condition κg(s)≠0.Moreover,we can show that the curve γ(s)satisfies the condition κg(s)≡0if and only if there exists a lightlike vector csuch that γ(s)-cis a geodesic.Such a curve is called an equidistant curve.

3 Height functions

In the following,we introduce two families of functions on a curve γ:I→H+3lying on a spacelike surfaceM.Suppose thatwe can define these functions as follows:

3.1 Hyperbolic time-like height function

We call HT; the time-like height function of γon M= H+3(-1).We denote hυT(s)=HT(s,υ)for any fixedυ∈H+3(-1).We have

From Frenet formulae,we have

Sinceυ∈H+3(-1),there are λ,μ,ν∈Rsuch that υ =λγ(s)+μE1(s)+νE2(s),therefore 〈υ,υ〉=-1,hence

which implies λ=κgμ,and

then,we have

therefore

if and only if υ=λγ(s)+μE1(s)+νE2(s),-λ2+μ2+ν2=-1and λ=κgμ,it means that

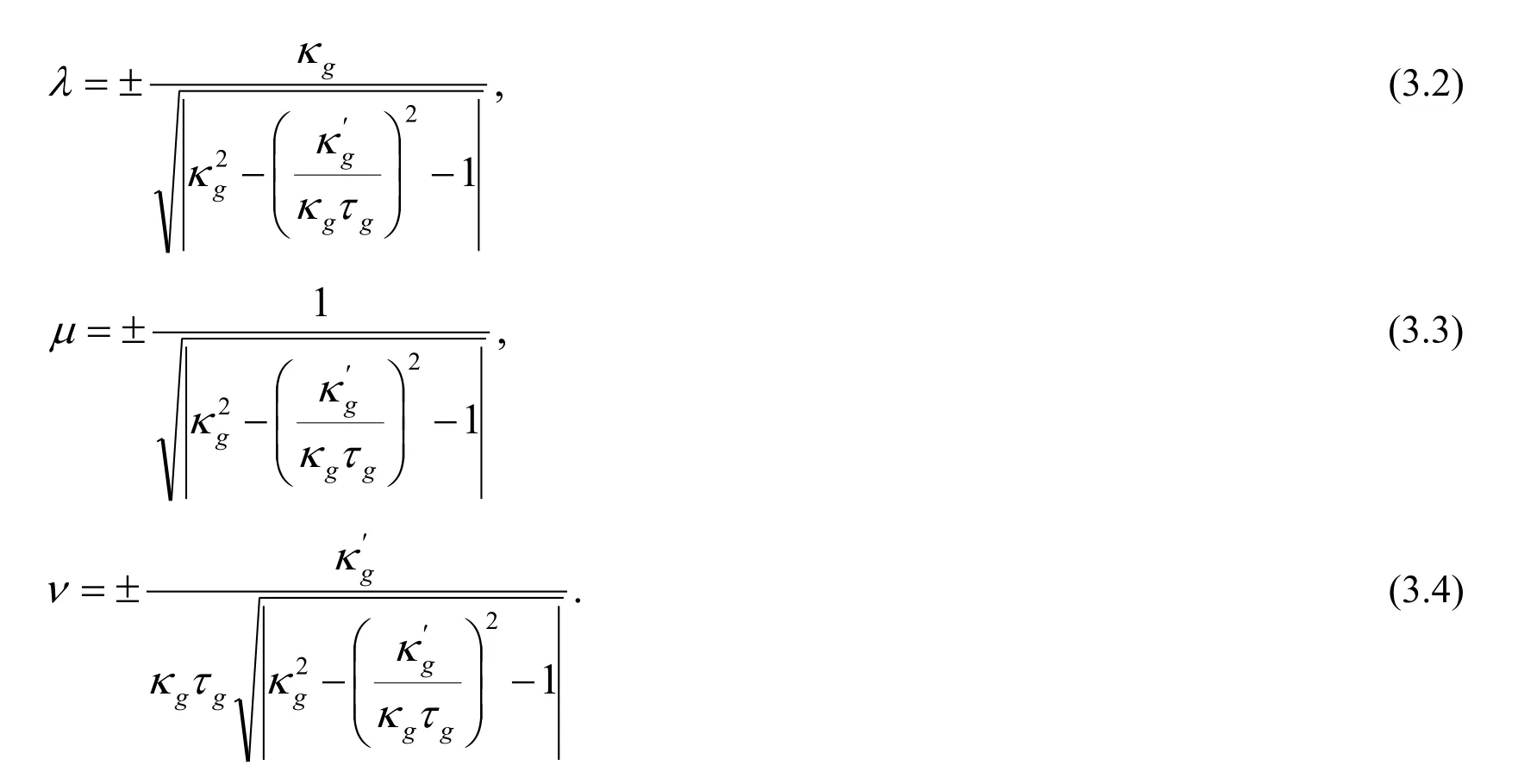
Since λ,μ,ν∈R,therefore we can consider under the condition Moreover,we obtain

and then

Differentiating Eq.(3.5)and using Eqs.(3.2)-(3.4),we get

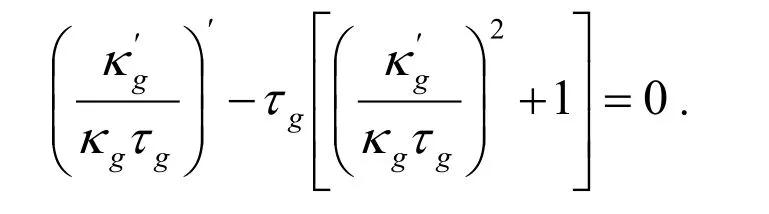
Now,we define σHas

If we calculate the fifth derivative of HT,we can show that the above conditions and

are equivalent to the conditions σH(s)=0and σ′H(s)=0.As a consequence,we have the following proposition.

Proposition 3.1 Suppose that T′(s)≠0.For any(s,υ)∈ I ×H+3(-1),we have

1)(hυT)′(s)=(hυT)′(s)=0if and only if υ=λγ(s)+μE1(s)+νE2(s)where λ,μ ,ν∈ Rsuch that -λ2+μ2+′ν2=-1.

2)(hυT)′(s)=(hυT)′(s)=(hυT)′(s)=0if and only if

3)(hυT)′(s)=(hυT)′(s)=(hυT)′(s)=(hυT)(4)(s)=0if and only if

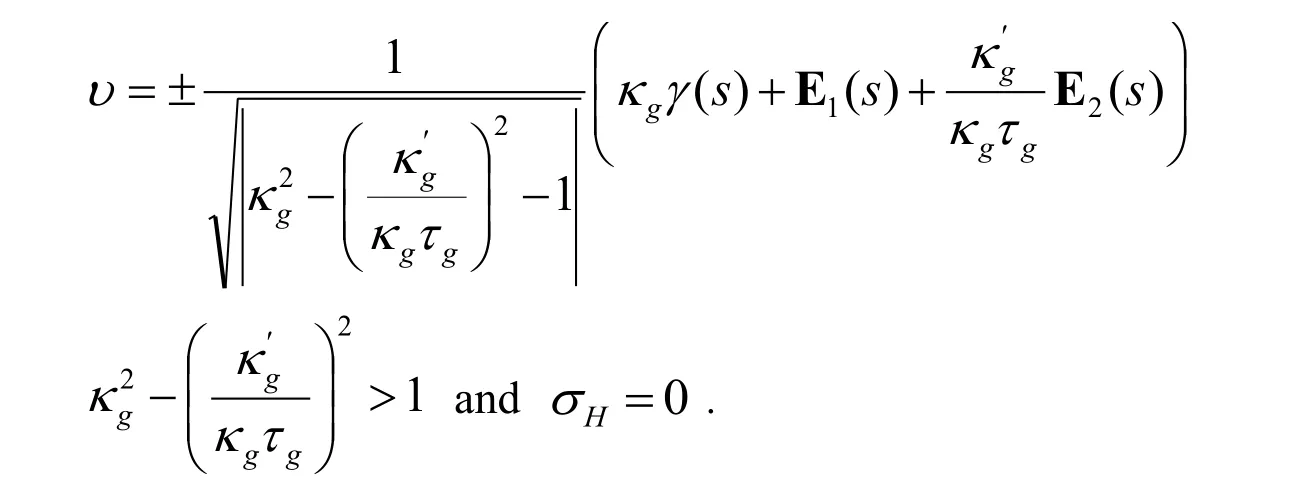
4)(hυT)′(s)=(hυT)′(s)=(hυT)′(s)=(hυT)(4)(s)=(hυT)(5)(s)=0if and only if

In the light of Proposition 3.1,we have the invariant σH.So,we define the curve hγ:I → H+3(-1)as follows

and we call it a hyperbolic evolute of γ relative to M.

By straightforward calculations,we havehγ′(s)=0,if and only if σH(s)≡0.Also,hγ=υ。is constant if and only if σH(s)≡0.

From Proposition 3.1,we have hυT。is constant,that is,there is a real number c ∈ Rsuch that 〈γ(s),υ。=c〉.It means that I mγ= P(υ。,c)∩M.It suggests that curves of the form P(υ,c)∩Mfor υ∈H+3(-1)are the candidates of model curves onM.

These curves play a similar role to curves in Euclidean space and call them(hyperbolicslices or H-slices)of M.

3.2 De Sitter space-like height function

We call HS; the spacelike height function of γ on M,where

HS:I ˄S13→R;(s,υ)↦(γ(s),υ).

We denote hυS(s)=HS(s,υ)for any fixed υ ∈S13,and by using Frenet-Serret formulae,we get

Since υ ∈S13,therefore there exist λ,μ,ν∈R,such that

where υ ∈S13,then 〈υ,υ〉=1,so we have

this leads to

Also,we have

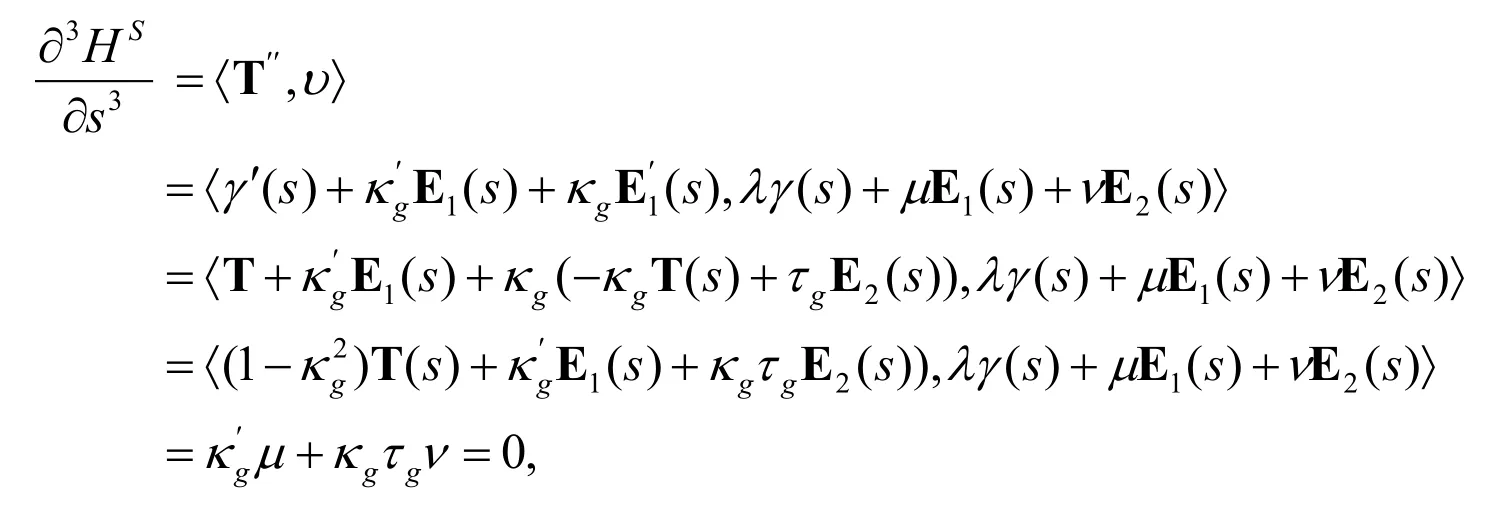
therefore

Hence,the following is satisfied

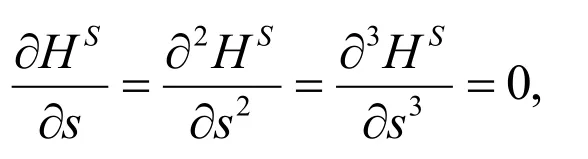
if and only if υ=λγ(s)+μE1(s)+νE2(s),-λ2+μ2+ν2=1and λ=-κgμ,it means that

Since λ,μ,ν∈R,therefore we can consider the conditionso we have

Moreover,

then

After using the values of λ,μand νin Eq.(3.8),we obtain

therefore,we can show that the above conditions with the extra condition:

are equivalent to the conditions σD(s)=0and σ′D(s)=0.As a consequence,we have the following proposition.

Proposition 3.2 If T′(s)≠0.Then,for any(s,υ)∈I×S12,we have

1)(hυS)′(s)=(hυS)′(s)=0if and only if υ=λγ(s)+μE1(s)+νE2(s),where λ,μ,ν∈R;-λ2+μ2+ν2=1.

2)(hυS)′(s)=(hυS)′(s)=(hυS′)′(s)=0if and only if

3)(hυS)′(s)=(hυS)′(s)=(hυS)′(s)=(hυS)(4)(s)=0if and only if

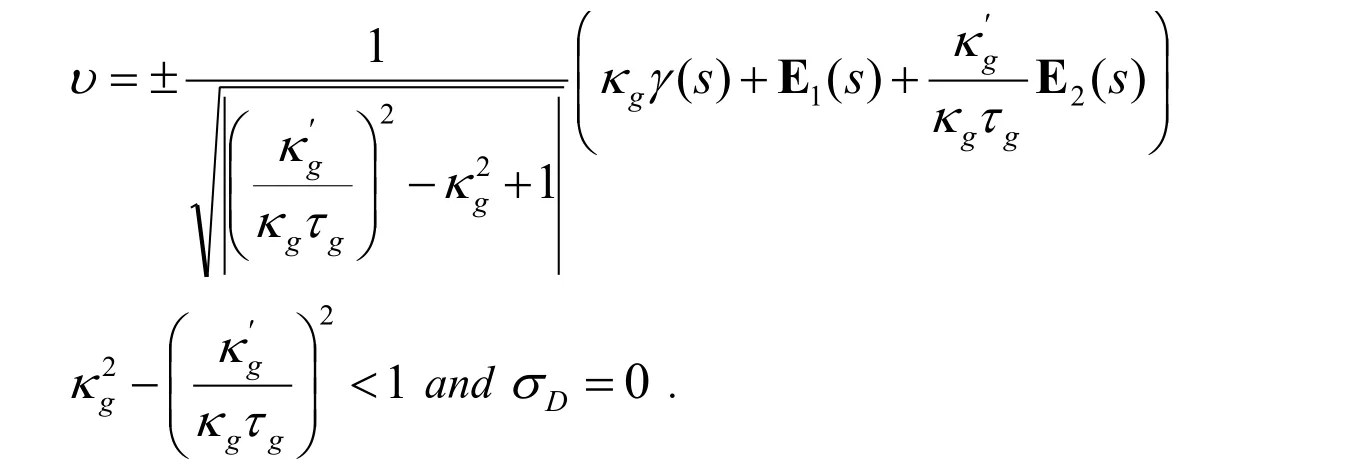
4)(hυS)′(s)=(hυS)′(s)=(hυS)′(s)=(hυS)(4)(s)=(hυS)(5)(s)=0,if and only if

According to this proposition,we have the invariant of σD.So,we define the curve dγ: I →S13by

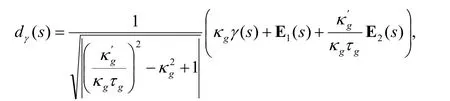
and we call dγ; a de Sitter evolute of γrelative toM.

By straightforward calculations,we have dγ′(s)=0if and only if σD(s)=0.Therefore,d=υis constant if and only if σ(s)≡0.Using Proposition 3.2,we have hTγ。is constant,that is,there is a real number c ∈Rsuch that 〈γ(s),υ。=c〉.It means that Imγ= P(υ。,c)∩M .It suggests that curves of the form P(υ,c)∩Mfor υ ∈S13are the candidates of model curves on M.Also,these curves play a similar role to curves in Euclidean space and we call them(de Sitter-slices or D-slices)of M.

3.3 Hyperbolic(De Sitter)invariants of curves

In this section,we study the geometric properties of the hyperbolic evolute of a curve in H+3.For any r ∈Rand υ。∈H+3or υ。∈S13,we denote

PS1(υ。,r)={υ∈H+3|〈υ,υ。〉=r},and we call it a pseudo-sphere in H+3with center υ。.

Proposition 3.3 If γ:I→H+3be a unit speed curve with κg′≠0.Then,τg≡0if and only if

and γis a part of a pseudo-sphere in H+3whose center is υ。.

Proof.We denote

then,we have

Therefore,P±(s)′≡0if and only if τg≡0.Under this condition,we put

and

Thus,it is easy to show that γ(s)is a part of the pseudo-sphere PS1(υ。,r).

Let γ:I→H+3be a unit speed curve withFor any s。∈I,we consider the pseudo-sphere P S1(υ。,r。±)where υ0=hγ(s)and

Therefore,we can give the following proposition.

Proposition 3.4 Under the above assumptions,γand P S1(υ。,r。)have at least 4-points contact at γ(s。).

Proof.We assume that P S1(υ。,r。)⊂H+3.In this case,we consider the hyperbolic timelike height function HT.By definition,we haveProposition 3.1(2)means that γand P S1(υ。,r。)have at least a 4-point contact at γ(s。)Ifthen we adopt the hyperbolic spacelike height function HS,and the assertion follows from exactly the same arguments as those of the previous case.

We call P S1(υ。,r。)in Proposition 3.4,the osculating pseudo-sphere(or,the pseudo-sphere of geodesic curvature); its center υ。is called the center of geodesic curvature.So,the hyperbolic evolute is the locus of the center of geodesic curvature.

4 Unfolding of functions of one variable

In order to investigate the singularities of pseudo-spherical evolutes,we apply the theory of unfolding of functions.First,we give a quick review on this theorem of one variable.Detailed descriptions are found in Bruce et al.[Bruce and Giblin(1992); Izumiya(2013)].

for i= 1,...,r.Then,F is called a(p)versal unfolding if the(k-1)×rmatrix of coefficients α(ji)(j= 1 ,...,k-1)has rank k -1;(k-1≤r).Under the same condition as the above,Fis called an ℜ-versal unfolding if the k ×rmatrix of coefficients(α0i,αji)has rank k(k ≤r),where

Now,we introduce an important set concerning the unfolding relative to the above notions.The bifurcation set BFof F is

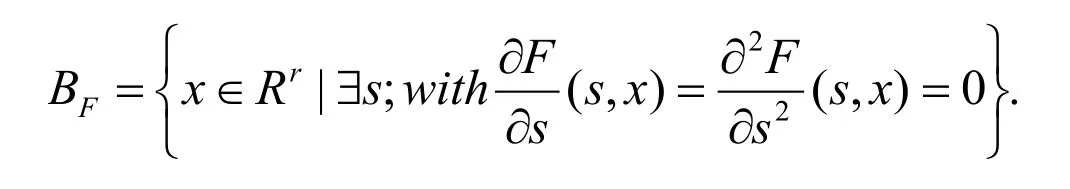
Therefore,we have the following fundamental result of the unfolding theory.

1)If k=3,then BFis locally diffeomorphic to C × Rr-2,

2)If k=4,then BFis locally diffeomorphic to S W × Rr-3,

where C={(x1,x2)|x12=x23}is the ordinary cusp(see Fig.1)and

SW={(x1,x2,x3)|x1=3u4+u2v,x2=4u3+2uv,x3=v},

is the swallowtail surface(see Fig.4).

Figure 1:The ordinary cusp

We consider that HT(s,υ)(respectively,HS(s,υ))is an unfolding of(s)(respectively,(s)).So,we have the following proposition.

Proposition 4.1 Let γ:I→H+3be a unit speed curve withThen,we have

Proof.We denote γ(s)=(x1(s),x2(s),x3(s),x4(s)),

HT(s,υ)=it follows that

From Proposition 3.1,hυT(s。)has a type A4at s。if and only if

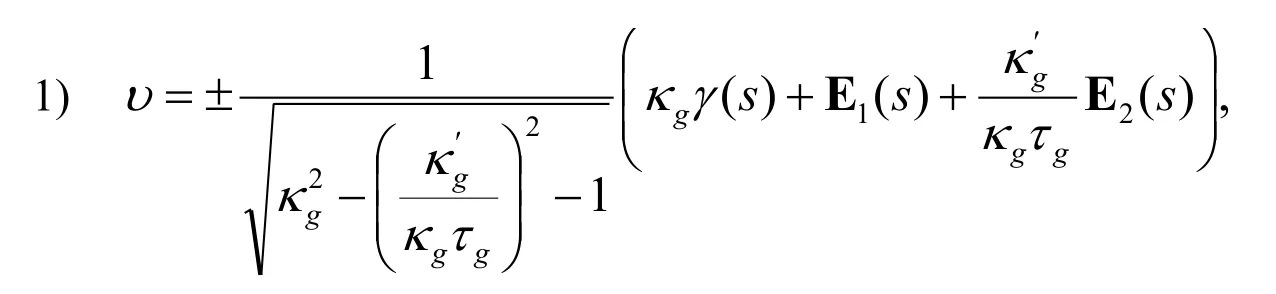
For this purpose,the following matrix

must be non-singular.Therefore,we calculate the determinant of it as follows

or in another form

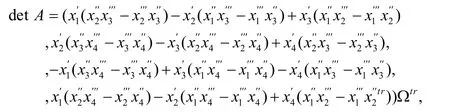
where

and Ωtris the transpose of a matrix Ω.Then we get

by using Frenet formulae,we can write

where

then we have

By the same way as the above,if we consider the spacelike height function HS,we can prove Proposition 4.1(2).

Theorem 4.2 Let γ:I → H+3(-1)be a regular curve such thatThen we have the following assertions:

(A1)The hyperbolic evolute at hγ(s0)is regular if σH(s0)≠0.

(A2)The following conditions are equivalent:

1.The germ of the hyperbolic evolute at hγ(s0)is diffeomorphic to a Swallowtail surface,

2.σH(s0)=0and σ′H(s0)≠0,

(B1)The de Sitter evolute at dγ(s0)is regular if σD(s0)≠0.

(B2)The following conditions are equivalent:

1.The germ of the de Sitter evolute at dγ(s0)is diffeomorphic to a Swallowtail surface,

2.σD(s0)=0and σ′D(s0)≠0,

Proof.(A1)By the assertion of Proposition 3.1,we have hγ′(s)=0if σH(s)=0.It means that the hyperbolic evolute at hγ(s)≠0is regular if σH(s)≠0.

(A2)By Proposition 3.1,the bifurcation set of HTis

By Theorem 4.1 and Proposition 4.1,the germ of the bifurcation set is diffeomorphic to a Swallowtail surface if σH=0and σ′H≠0.Moreover,we have other equivalences from Proposition 3.3 and Proposition 3.4.This completes the proof of(A1)and(A2).If we consider the spacelike height function HS,then we can prove the remaining assertions of the theorem.

5 Computational examples

In this section,we consider some illustrative examples to explain the evolute curve on a surface of graphical representation in H+2(-1)and H+3(-1).From Theorem 4.1,the evolute curve in H+2(-1)at hγ(s0)is regular if σH≠0,and is the ordinary cusp locally if σH=0,and σH′≠0,see Example 5.1 and Example 5.2 .

Example 5.1 In H+2(-1),we have the hyperbolic Frenet formulae of a curve γ:

where κgis the geodesic curvature of γin H+2,which is given by

The hyperbolic evolute of γis given by

Here,we have

Now,suppose that X(u,v)=(u2,u3,v)be a cuspidal edge surface,see Fig.2.We investigate the following curve

From Eq.(5.3),we have

Since E=γ˄T ,therefore we get

therefore,we have

from Eqs.(5.3),(5.4)and(5.7),we get

Then,we have

and so

At the point u=0,we have

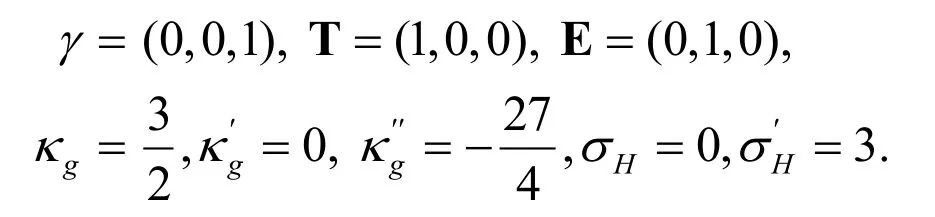
Thus,the hyperbolic evolute of γhas a cusp at the origin.

Now,we find the equation of the hyperbolic evolute curve of cuspidal edge surface.From Eqs.(5.2),(5.3),(5.6)and(5.8),we have

Figure 2:The curve γ,Cuspidal edge surface Ψ

Example 5.2 In this example,we consider a spacelike curve γ(s)lying fully on an oriented ruled surface Ωin H+2(-1),as follows

(see Fig.3).We investigate the following curve:

it follows that

From Eq.(5.11),we get

where E=γ˄T ,and we get

therefore,we have

using Eqs.(5.9),(5.11)and(5.13),we get

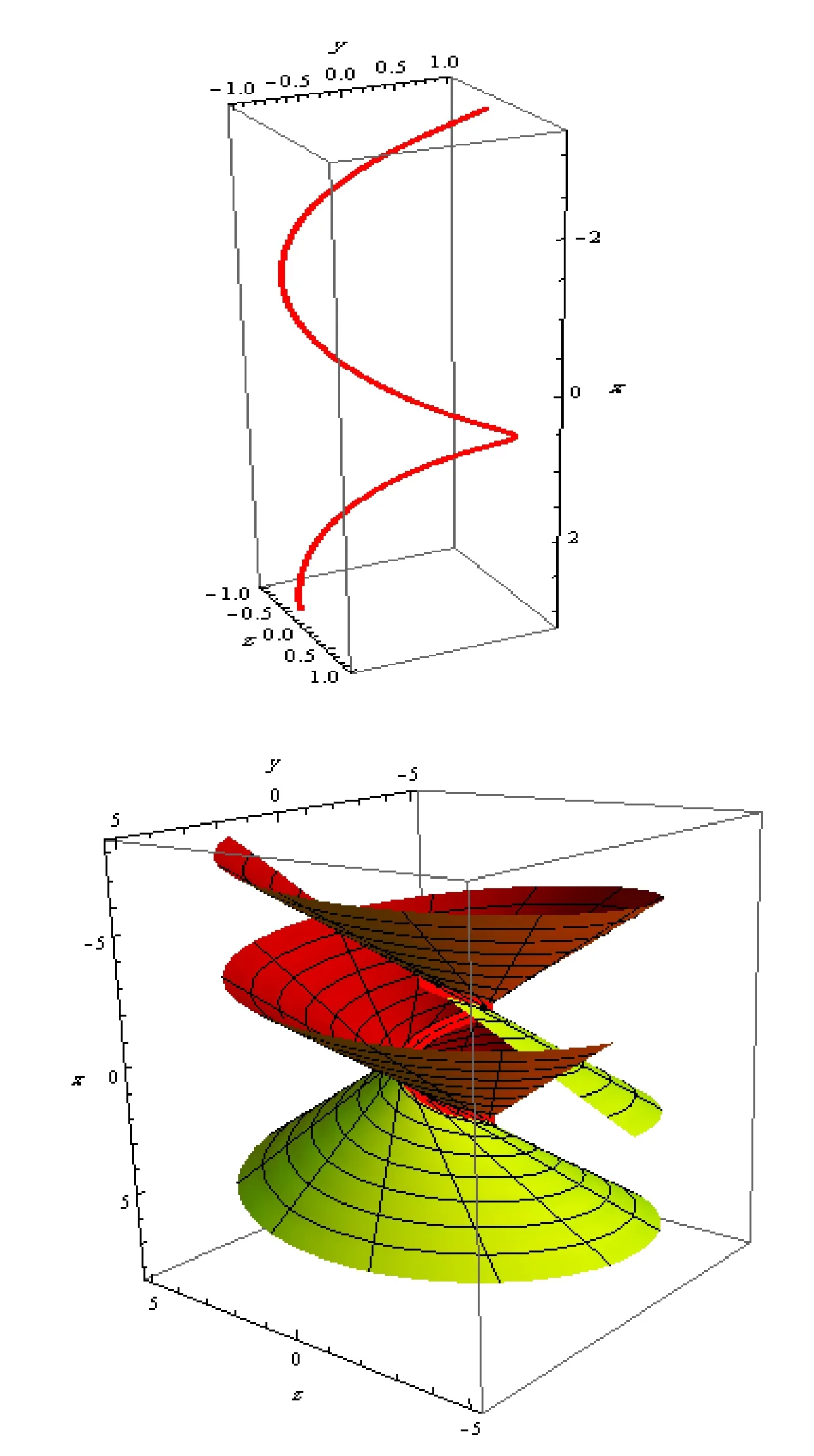
Figure 3:A spacelike curve γ(s)lying fully on an oriented ruled surfaceΩ

Example 5.3 Suppose that Φ(u,v)=(3u4+u2v,4u3+2uv,v)be a Swallowtail surface(see Fig.4).In this example,we investigate the following curve βin H+3(-1):

it follows that

and

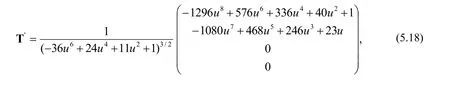
from Eqs.(5.16)and(5.18),we get

therefore

Then,from Eqs.(5.19)and(5.20),we get

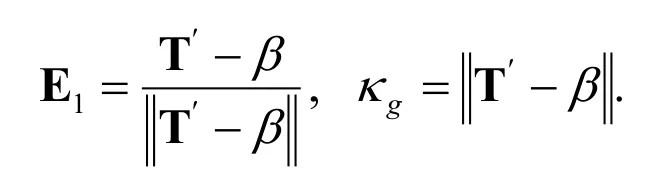
And we have

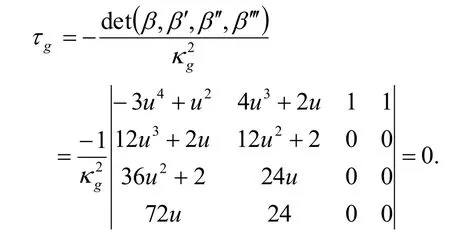
So,at the point u=0,we obtain

and

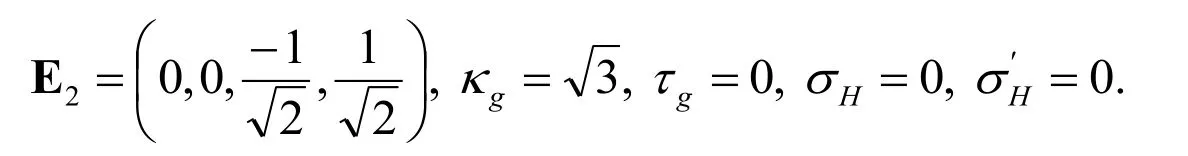
Finally,from the previous calculations,we can find the equation of the evolute curve in hyperbolic 3-space as given in Eq.(3.7).

Figure 4:The Swallowtail surface),(vuΦ

6 Conclusion

In the three dimensional hyperbolic space,the pseudo-spherical evolutes of curves are studied.Also,some relationships between singularities of these curves and geometric invariants under the action of the Lorentz group are obtained.Furthermore,some computational examples in support of main results are given and plotted.

Acknowledgment:The authors are very grateful to referees for the useful suggestions and remarks for the revised version.