基于融合GMM聚类与FOA-GRNN模型的推荐算法

李毅鹏，阮叶丽，张杰



基于融合GMM聚类与FOA-GRNN模型的推荐算法

李毅鹏，阮叶丽，张杰

（中南财经政法大学信息与安全工程学院，湖北 武汉 430073)

针对传统基于物品的推荐算法由于数据稀疏性导致的低推荐精度问题，提出了一种融合GMM聚类和FOA-GRNN模型的推荐算法。该算法首先使用高斯混合模型（GMM）方法对物品特征进行聚类；然后根据聚类结果分别构造评分矩阵，并使用Slope One算法填充评分矩阵；最后计算用户对物品的相似度预测评分作为输入，通过FOA-GRNN模型输出最终的评分。基于movielens-2k数据集的实验结果表明，与其他3种算法相比，该算法能够更好地处理高稀疏性数据，推荐精度更优，并能够在一定程度上解决冷启动问题。

推荐算法；GMM聚类；果绳优化；广义回归神经网络；Slope One算法

1 引言

随着互联网技术的发展，人们在线获取的数据越来越丰富，然而大量无关冗余数据严重干扰了人们对有用信息的选择，这种现象被称为“信息过载”。因此，推荐系统成为帮助用户获取有用信息的必要工具，其原理是基于用户的兴趣偏好、历史评分、需求、行为等信息产生一个排序序列，将排序靠前的商品或信息推荐给用户。近年来，越来越多的个性化推荐方法被相继提出，协同过滤推荐算法由于其推荐过程自动高效，并且仅利用用户对物品的评分信息而被广泛使用，成为互联网时代的新宠。协同过滤推荐算法有2种不同的推荐途径，分为基于用户的协同过滤和基于物品的协同过滤。

虽然协同过滤算法由于其简单、有效和准确性而被广泛应用，在信息时代节约了用户获取信息的时间代价，但是用户评分数据的稀疏性和冷启动问题成为制约其推荐精度的主要原因。对此，国外学者率先进行了相关研究，Deshpande等[1]提出SVD奇异值分解法可以对用户−项目评分矩阵进行降维，通过删除冗余信息实现降低数据稀疏度的目的。Rendle[2]则从贝叶斯原理出发，使用贝叶斯概率修正用户对项目的预测评分，降低了算法的预测偏差。Ocepek[3]就冷启动的问题，在传统协同过滤算法基础上加入用户认知信任信息，提升了推荐精度。国内学者在协同过滤推荐算法的研究上虽起步较晚，但已取得了可观的研究成果。张锋等[4]首先将机器学习的思想融入协同过滤算法中，利用BP网络降低数据稀疏度，取得了不错的实证效果。詹增荣[5]则通过RBF函数插值法对稀疏数据进行填补，接着采用SVM进行评分预测，使算法克服了数据质量的不足，增加了稳定性。张玉连等[6]另辟蹊径，提供了一种简单高效的优化方案。用最小二乘法对Slope One算法进行加权，从而实现对稀疏数据的填充。郭兰杰等[7]考虑到“朋友关系”可能影响不同用户对于物品的选择，故引入用户社交网络信息对物品相似度计算和最终预测评分阶段的缺失值进行填充，在降低评分误差的同时提高了分类准确率，但却增加了相关数据获取的难度以及算法整体的复杂性。针对传统协同过滤算法未充分重视用户反馈信息的问题，张宇等[8]提出了基于正负反馈的支持向量机协同过滤，筛选了用户较为喜欢的物品进行排序，加快了算法的推荐速度。庞海龙等[9]将真实评分与预测评分的插值作为线性回归模型的输入训练模型，从而产生最终推荐，为缓解数据稀疏性提供了另一种解决方案。与此同时，丁永刚等[10]提出码本聚类的思想获取用户评分风格信息，降低了推荐成本。龚敏等[11]利用-means方法对用户进行聚类，提高了推荐算法的可扩展性。陶维成等[12]则引入灰色关联度的聚类方法对物品特征进行聚类，取得了类似的实证效果。杨大鑫等[13]在上述研究的基础上，利用最小方差对-means算法进行优化后对用户聚类，对协同过滤算法做了进一步改进。

综上所述，国内外学者对协同过滤算法的改进大多是从稀疏矩阵的填充以及用户信息的扩展两方面提出，对物品特征之间的联系兼顾较少，或考虑到物品类别，但未对用户项目评分做进一步优化，并且对用户信息的扩展增加了数据获取的难度。因此，本文从物品特征出发，提出了融合高斯混合模型（GMM）聚类和果蝇优化−广义回归神经网络（FOA-GRNN）模型的推荐算法，结合物品特征信息以及广义回归神经网络（GRNN）模型的非线性拟合能力产生推荐。

2 融合GMM聚类和FOA-GRNN模型的推荐算法

基于高斯混合模型聚类算法、果蝇优化算法、广义回归神经网络，本文构建了融合GMM聚类和FOA-GRNN模型的协同过滤算法。整套算法以基于物品的协同过滤算法为核心加以优化，算法构建的基本流程细化如下。

2.1 基于物品特征的GMM聚类

相较于-means等传统的聚类方法，GMM聚类不用指定类别的个数，将样本特征假设为服从高斯分布，在大样本条件下更符合中心极限定理，最终的聚类结果是每个样本分属于不同类别的概率，相较于-means聚类更为合理，同时GMM算法的时间复杂度较-means有所减小，降低了算法运行开销。

2.2 计算物品相似度以及用户−物品预测评分

2.2.1 结合GMM聚类结果计算物品间相似度

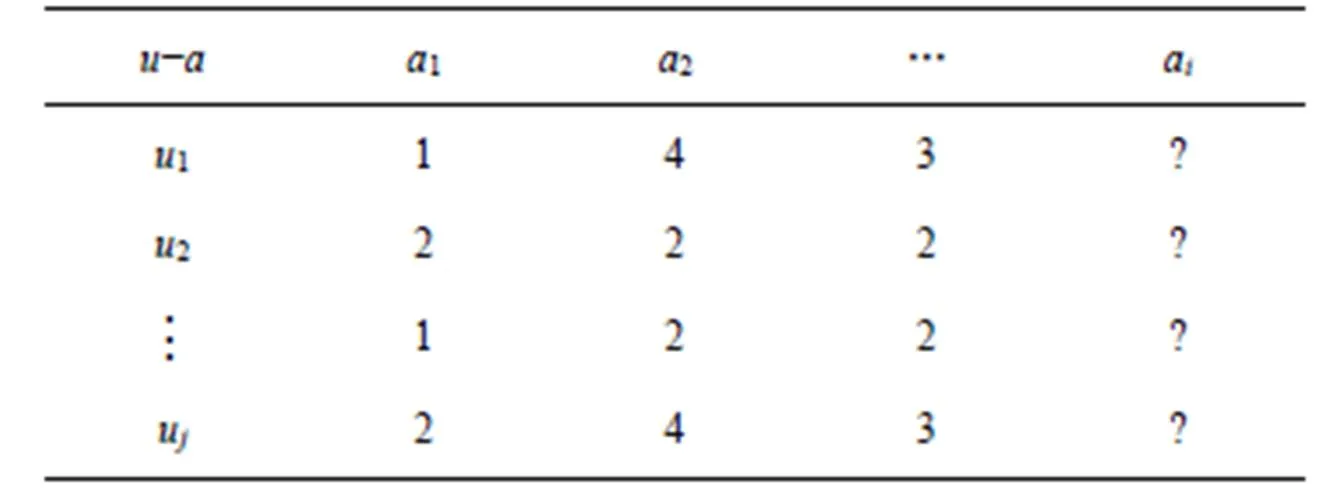
表1 用户−物品评分矩阵

与传统协同过滤算法只通过用户评分矩阵计算物品之间相似度不同，本文提出的算法结合了对物品特征进行GMM聚类的结果，将物品的特征信息深入融合到物品相似度计算中。根据2.1节的假设，所有物品被聚为类，对于每一类中的物品，分别计算其与同属于一类中的其他物品的相似度，相似度采用常用的皮尔逊相似度度量，即

2.2.2 基于物品相似度预测评分

在相似度计算的基础上，通过用户对物品的最相似邻居的评分值进行相似度加权后得到用户对物品的评分预测值，计算公式如下。

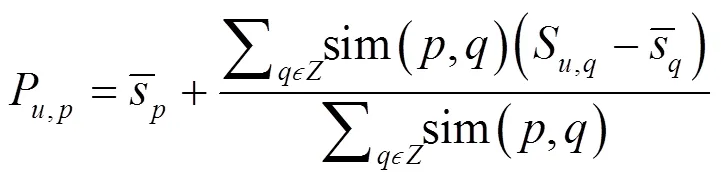
其中，表示物品的最相似邻居集合。

2.2.3 Slope One算法填充缺失值

由于用户评分矩阵的高稀疏性，对式(1)、式(2)的计算有所不便。在此采用Lemire等[14]于2005年提出的一种有效的缺失值填充方法，即Slope One算法[14]，本文在式(1)、式(2)的计算过程中采用Slope One算法对可能的缺失值进行选择性填充，Slope One算法重复利用用户−物品评分矩阵中已评分数据，计算相关的未评分数据以改善数据的稀疏性。

2.3 FOA-GRNN模型预测最终评分

用户−物品评分矩阵中的缺失值由式(2)的计算结果代替，将所有相似度预测评分作为GRNN模型的输入，以聚类结果为依据，按物品所属类分别训练FOA-GRNN神经网络模型，以FOA-GRNN神经网络模型的输出结果作为最终的预测评分。

表2 第类用户对物品评分信息

2.4 评价指标

本文选用推荐算法常用的2种评价指标来评价算法推荐结果的优劣[15-16]，这2种评价指标分别为平均绝对误差（MAE）和均方根误差（RMSE），即

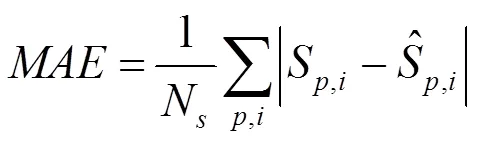
3 实验分析

3.1 实验数据集

本文采用的实验数据集是推荐系统常用的movielens-2k数据集，包含在HetRec2011 Dataset中。该数据集是movielens 10M数据集的扩展，包含更多的电影特征信息。除了基本的“release time”“genre”外，还有“Top Critics Rating”“Top Critics NumReviews”“Top Critics Score”“Audience Rating”等连续型数据，相比movielens 10M数据集更加利于项目聚类算法的开展。该数据集的核心是2 113位用户对10 197部电影的评分，共855 598个记录，而每部电影只有84个评分记录，保证了高稀疏度的数据要求，因此，本文选用该数据集作为融合GMM聚类和FOA-GRNN模型推荐算法的实验数据集。

3.2 实验结果分析

对movielens-2k数据集的电影信息进行整理后发现，其可供聚类使用的有效特征数为16个，剔除其中含有的无效记录后可供研究的电影数目为10 105个，即整个实验的物品数目为10 105个，用户数目为2 111个，涵盖855 598个评分记录，其中不难发现实验数据集的评分稀疏度已达到96%。本文所提算法的第一步根据电影特征对10 105部影片进行聚类，由于电影特征数较多，在此先用PCA主成分分析法对电影特征进行降维，并识别出3个主成分，再对主成分进行GMM聚类。GMM聚类能够自动生成聚类的簇数，并不需要自己设定，最终的聚类结果如图1所示。

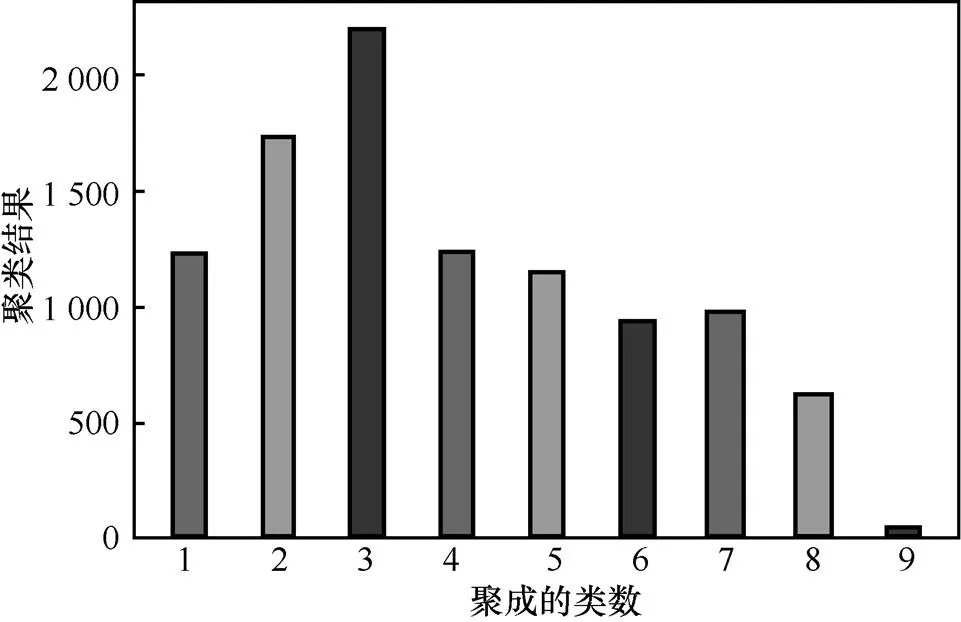
图1 GMM聚类结果

从图1中可以看出，GMM聚类根据电影特征信息将10 105部电影聚成9类，各个电影所属的类别根据EM算法计算出的最终概率而定。聚类结果中各类含有的影片数目大体较为均匀，其中含有电影数目最多的类是第3类，包含2 202部影片，而所含电影数目最少的类别为第9类，仅有39部电影。

根据上述聚类结果，分别对每个类别中的物品计算相似度，再根据每个物品的相似度大小进行排序，构建每个物品的最相似物品邻居集合，计算过程的缺失值使用Slope One算法选择性填充，以相似度为基础计算出的用户−物品预测评分作为FOA-GRNN神经网络模型的输入，得到最终的预测评分信息。其中，FOA算法对GRNN模型平滑因子进行迭代寻优的过程如图2所示。

图2 FOA优化GRNN迭代路径

根据MAE和RMSE这2种推荐算法优劣的评价指标，本文计算了在每一类中训练出的FOA-GRNN模型的MAE值和RMSE的值，根据文献[7]，本文将物品的相似度邻居数设置为30进行对比，每一类的MAE和RMSE值均为5折交叉验证的平均结果，如图3所示。

图3 各个类中的RMSE和MAE值

从图3可以看出，各个类别的MAE值和RMSE值较为稳定，其中的少许波动一定程度上是由于各类样本数大小不同引起的，其中，第4类中的用户−电影评分矩阵的稀疏程度较大，故得到较大的MAE和RMSE，相对正常。总体来看，RMSE值略大于MAE，RMSE和MAE指标均未出现极端值，这也说明本文提出的推荐算法具有较高的泛化能力。

为了进一步比较验证本文提出的算法与已有的推荐算法性能的优劣，这里分别将新算法与如下3种算法的性能进行对比分析，所用的评价指标依然是MAE和RMSE。

第1种算法为传统的基于物品的协同过滤算法（UCF），只根据用户−物品评分矩阵计算物品之间的相似度，进而根据物品的最相似集合计算用户对物品的预测评分。

第2种算法为采用-means算法对物品聚类，然后采用FOA优化GRNN模型得出最终预测评分的算法，即在本文算法的基础上，将GMM聚类算法替换为-means算法后得到的算法，以比较-means算法和GMM算法在处理本文问题的表现优劣，记为-FOA-GRNN。

第3种算法为本文算法中的FOA优化GRNN模型替换为传统的BP神经网络模型，以预测最终的评分值，以此比较FOA-GRNN模型同BP模型在本文问题上的预测效果，记为GMM-BP。

采用相同的数据集实验后，4种算法的对比结果如图4和图5所示。其中，横轴代表相似度邻居数，纵轴则表示误差MAE和RMSE值。

图4 4种算法MAE值对比

图5 4种算法RMSE值对比

由图4和图5可以看出，随着物品相似度邻居的增加，每种算法的MAE值和RMSE值都有一个先降后升的趋势，在邻居数为30时，MAE和RMSE都达到一个最小值。与其他3种已有算法相比较，本文提出的算法无论在MAE还是RMSE上，均小于其他3种已有算法，MAE和RMSE值均有较大幅度的降低，在各个邻居数下皆是如此。因此，本文提出的新算法较已有的协同过滤算法，有更好的推荐性能，适用范围更加广泛。

4 结束语

本文在已有研究的基础上，提出了一种融合GMM聚类与FOA-GRNN模型的协同过滤算法。该算法以传统面向物品的协同过滤算法为核心，充分利用物品特征的信息反馈，先通过GMM聚类方法将物品进行聚类，再根据聚类结果计算各个类别的物品之间的相似度，并用Slope One算法对计算过程的确实值进行填充，缓解了数据的稀疏性问题。最后将基于物品相似度邻居集合计算出的用户对物品的预测评分作为GRNN模型的输入，利用FOA算法对GRNN模型的平滑因子进行迭代寻优，从而获得最终的用户物品预测评分，得益于GRNN模型多变量输出功能，可以较为有效地解决评分稀疏性问题。在movielens-2k数据集上的实证分析显示，改进的算法推荐误差较小，精度较高，并且较其他3种协同过滤算法有更好的推荐能力和泛化能力。

[1] DESHPANDE M, KARYPIS G. Item-based top-, recommendation algorithms[M]. ACM, 2004.

[2] RENDLE S, FREUDENTHALER C, GANTNER Z, et al. BPR: Bayesian personalized ranking from implicit feedback[M]. AUAI Press, 2009:452-461.

[3] OCEPEK U, RUGELJ J, BOSNIĆ Z. Improving matrix factorization recommendations for examples in cold start[J]. Expert Systems with Applications, 2015, 42(19):6784-6794.

[4] 张锋, 常会友. 使用BP神经网络缓解协同过滤推荐算法的稀疏性问题[J]. 计算机研究与发展, 2006, 43(4):667-672.ZHANG F, CHANG H Y. Employing bp neural networks to alleviate the sparsity issue in colaborative filtering recommendation algorithms[J]. Journal of Computer Research and Development,2006, 43(4):667-672.

[5] 詹增荣, 曾青松. 基于协方差矩阵表示的图像集匹配[J].湖南师范大学自然科学学报,2015, 38(4):74-79.ZHAN Z R, ZENG Qing-song image set matching based on covariance matrix[J]. Journal of Natural Science of Hunan Normal University, 2015, 38(4): 74-79.

[6] 张玉连, 郇思思, 梁顺攀. 融合机器学习的加权Slope One算法[J].小型微型计算机系统, 2016,37(8):1712-1716.ZHANG Y L, HUAN S S, LIANG S P, 
Integrating machine learning into weighted Slope One algorithm[J]. Journal of Chinese Computer Systems, 2016, 37(8): 1712-1716.

[7] 郭兰杰, 梁吉业, 赵兴旺. 融合社交网络信息的协同过滤推荐算法[J]. 模式识别与人工智能, 2016, 29(3):281-288.GUO L J, LIANG J Y, ZHAO X W. collaborative filtering recommendation algorithm incorporationg social network information[J]. PR&AI, 2016, 29(3): 281-288.

[8] 张宇, 王文剑, 赵胜男. 基于正负反馈的SVM协同过滤Top-推荐算法[J]. 小型微型计算机系统, 2017, 38(5):961-966.ZHANG Y, WANG W J, ZHAO S N. SVM collaborative filtering Top-recommendation algorithm based on positive and negative feedback[J]. Journal of Chinese Computer Systems, 2017, 38(5): 961-966.

[9] 庞海龙, 赵辉, 李万龙, 等. 融合协同过滤的线性回归推荐算法[J].计算机应用研究, 2019(5).PANG H L, ZHAO H, LI W L, et al. Linear regression recommendation algorithm with collaborative filtering[J]. Application Research of Computers , 2019(5).

[10] 丁永刚, 李石君, 余伟, 等. 基于码本聚类和因子分解机的多指标推荐算法[J]. 计算机科学, 2017, 44(10):182-186.DING Y G, LI S J, YU W, et al. Multi-criteria recommendation algorithm based on codebook-clustering and factorization machines[J]. Computer Science. 2017, 44(10): 182-186.

[11] 龚敏, 邓珍荣, 黄文明. 基于用户聚类与Slope One填充的协同推荐算法[J]. 计算机工程与应用. 2018, 20(8):102-110.GONG M, DENG Z R, HUANG W M. Collaborative recommendation algorithm based on user clustering and Slope One filling[J]. Computer Engineering and Applications, 2018, 20(8): 102-110.

[12] 陶维成, 党耀国. 基于灰色关联聚类的协同过滤推荐算法[J]. 运筹与管理, 2018(1):84-88.TAO W C, DANG Y G. Collaborative filtering recommendation algorithm based on grey incidence clustering[J]. Operations Research and Management Science, 2018(1):84-88.

[13] 杨大鑫, 王荣波, 黄孝喜, 等. 基于最小方差的K-means用户聚类推荐算法[J]. 计算机技术与发展, 2018(1):104-107.YANG D X, WANG R B, HUANG X X, et al. K-means user clustering recommendation algorithm based on minimum variance[J]. Computer Technology and Development, 2018(1): 104-107.

[14] LEMIRE D, MACLACHLAN A. Slope One Predictors for online: rating-based collaborative filtering[C]//Proc of SIAM Data Mining. 2005: 471-476

[15] BREESE J S, HECKERMAN D, KADIE C. Empirical analysis of predictive algorithm for collaborative filtering[R]. MSR-TR-98-12, Redmond, Microsoft, 1998.

[16] SEHAFER J, FRANKOWSKI D, HERLOCKER J. Collaborative filtering recommender systems[M]. Berlin: Springer. 2007.

Recommendation algorithm based on GMM clustering and FOA-GRNN model

LI Yipeng, RUAN Yeli, ZHANG Jie

School of Information and Safety Engineering, Zhongnan University of Economics and Law, Wuhan 430073, China

Aiming at the problem of low recommendation accuracy caused by sparse data in traditional item-based recommendation algorithm, a recommendation algorithm based on GMM clustering and FOA-GRNN model is proposed. The algorithm firstly uses Gaussian mixture model (GMM) to cluster the item features, then constructs the score matrix according to the clustering results, and fills the score matrix with slope one algorithm. Finally, the user's score based on similarity prediction is taken as input, and the final score is output through FOA-GRNN model. Experimental results based on movielens-2k dataset show that the proposed algorithm can deal with highly sparse data better and has better recommendation accuracy than the other three algorithms.

recommendation algorithm, GMM clustering, FOA, GRNN, Slope One algorithm

TP311

A

10.11959/j.issn.2096-109x.2018097

2018-11-10；

2018-11-29

阮叶丽，yeli_ruan@126.com

校级中央高校基本科研基金资助项目；教育教学改革基金资助项目（No.2018-9）

The Fundamental Research Funds for the Central Universities,The Education and Teaching Reform Fund (No.2018-9)

李毅鹏（1980-），男，湖北武汉人，中南财经政法大学副教授，主要研究方向为管理信息系统、DSS、Mobile电子商务。

阮叶丽（1994-），女，贵州仁怀人，中南财经政法大学硕士生，主要研究方向为推荐系统。

张杰（1995-），男，安徽六安人，中南财经政法大学硕士生，主要研究方向为金融统计。