模糊神经网络在配送中心选址中的应用研究

李 萍

(山西大同大学浑源师范分校，山西 浑源 037400)

0 引言

伴随我国经济的飞速增长和人民现对物质文化的需求，各实体间的交往逐渐频繁，物流配送已经在现实生活中起到了承上启下的作用。由于在物流配送中心的建设过程中所要涉及的因素较多，并且有很大的风险，所以如何选址成为很重要的问题。长期以来，研究人员不断的研究和探索，总结出多种算法；结合层次法的模糊排序方法、模糊综合评价法以及AHP层次分析法等，虽然以上方法可以用于解决选址问题，但是还并不能彻底解决，因为我们所研究的问题之间往往存在着依存关系，比如地价，运输的条件和环境等一系列问题[1-4]。

论文主要研究基于模糊神经网络的配送中心选址决策问题，概述了模糊神经网络基本原理以及影响物流配送中心选址决策的主要因素，利用MATLAB进行神经网络训练，从中可以得到对待评价方案的评价值，以便于选出最佳方案和最差方案。

1 BP模糊神经网络

BP模糊神经网络按照不同的功能可以将其分为输入层、中间层以及输出层，所以一般规定，一层的只能是输入和输出层，中间层比较特殊，中间层既可以只有一层也可以是多层的[5-8]。在相同的层之间是没有网络连接结点的。而且每一个网络的结点就表示一个神经元，所以用于传递的函数一般是Sigmoid型函数。同样，如果我们将BP神经网络当成非线性的映射来考虑，这样输入到输出的对应度会很高，把这样的输入以及输出的样本表示出来，就可以找到某一映射函数g与之相对应，可以得到g(xi)=yi,i=1,2,3,…,n，在这里n为样本的数模，BP模糊神经网络的结构如图1所示。

图1 BP模糊神经网络的结构示意图

神经元的传递用Sigmoid型函数进行计算，表示如下：

(1)

优化的目的就是要让误差函数达到最低或者是最小，如果想要达到这一目的就要对神经网络的输入值和输出值进行比较，两者之间的差函数通过比较可以直观地得出，接下来只要调节各层的链接的权值和各神经的阈值，就可以将误差函数降到最低，这种调节的过程被命名为误差反向传播BP算法，由于是从后向前进行的，所以具体的步骤可以参考下面的模型。

中间层的输出值可以表示成：

(2)

n代表的就是输入层的数目，其中k代表的是学习过程的次数，θj表示的是阈值(中间层单元)、这里的P表示的是单元的数目，wij表示的是连接的权值(输入层到中间层)，最后的xi表示的是输入值。

对于输出层而言，其输出值可以表示如下：

(3)

vjt代表的是连接权值(中间层至输出层)，rt代表的是阈值(输出层)、q代表的是单元数(输出层)。

2 配送中心选址中的评价决策问题

2.1 影响选址的主要因素

能够影响配送中心选址的因素可以总结为：用户的分布位置、商家的分布位置、运输的距离是否合理、候选地价格的高低、使用面积的大小、地质条件的优劣、不同的通讯条件以及道路的设施等。

2.2 物流配送中心选址的一般步骤

首先我们要在某一地区设置有多种商品的物流中心，当然这些都是假设的，也是要进行系统的研究和分析。现在假设我们只有一种产品，并且是由m个厂家Ai(i=1,2,…,m)供货，其中每个厂家所需要的物流量用ai表示；如果有n个需求点用Bj(j=1,2,…,n)表示，并假设各个需求点的物流总量用bj表示；如果需要对q个可能的物流据点进行选址，我们就可以表示成Ck(k=1,2,…,q)；大家都清楚需求点的进货方式，一般分为两种：第一种是最直接的，也就是从厂家直接进货；第二种就是从物流中心中转进货。假设仓库的存储费用、物流运费率以及据点投资费已知，根据前面的描述，为了达到最低成本Z，我们可以通过构建下面的函数数学模型来实现。

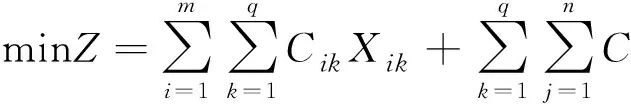
(4)

各个参数名称及含义如表1所示。

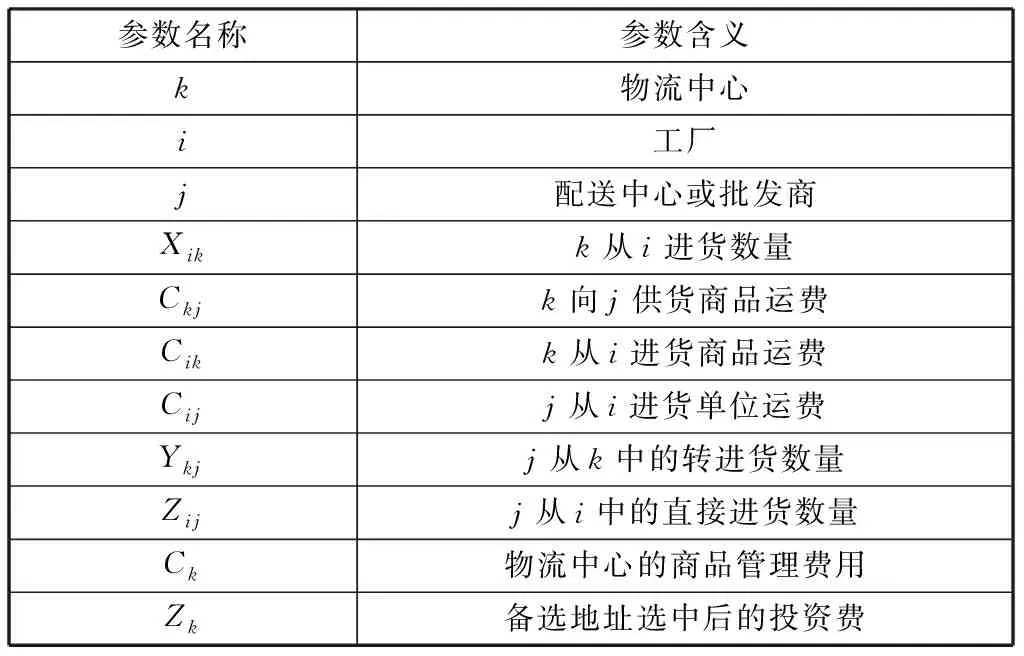
表1 参数含义

那么约束条件就可以表示为：

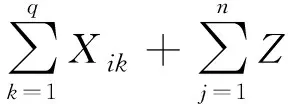
(5)

式(5)表示从上游工厂中运出的产品总量生产能力的最大值。

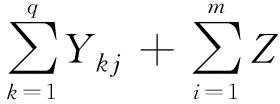
(6)

式(6)表示配送中心的需求量不能多于它运入的商品量。

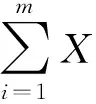
(7)

式(7)中Wk，M表示决策变量，Wk取值为0或1，当Wk取值为0表示第k物流中心被淘汰(备选)，当Wk取值为1表示该物流中心是被选中的；并且M是很大的正数。

(8)

式(8)表示每一个物流中心进出的商品总量是平衡的。

Xik，Ykj，Zij≥0.

(9)

如果需要对以上的式子进行修正，我们可以引入代表品种数量的其他参数，这样它就能适用于多种商品的物流中心。

3 基于模糊神经网络的配送中心选址的MATLAB实现

表2是收集到的已正在运营的十个物流配送中心相关指标的详细数据。

表2 评价样本

表2是在量化和模糊处理下得到的最优的权值矩阵，可直接引用于配送中心选址的评价应用中。

1) BP模糊网络模型建立

因为指标体系需求量实际需要八个，所以输入层必须设计成八个结点，输出层的结点数设计成为一个。由Kolmogorov可知，中间层设计可为一层。Tansig是适用于BP模糊网络训练的可微函数，是从(-∞,+∞)映射到(-1,+1)的隐含层传递函数。应用实例中的输出层只要设计一个结点即可，因为输出的期望值范围在(0,1)之间，所以输出层的传递函数可用logsig更为合适。

2) BP模糊网络训练

当隐含层结点数目取17时，选择trainlm函数，对网络进行实际训练，训练结果如图2所示。

图2 隐含层结点数为17的训练结果

如图2，经过4次训练后可以明显地观察到，误差逼近0.001。

3) 评价备选方案

在训练中输入五个待评价方案的评价矩阵的数据，在BP模糊神经网络中计算出各自的五个输出值，如图3。

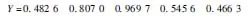
图3 计算结果

通过输出值的大小对备选方案的优劣排序，如表3。

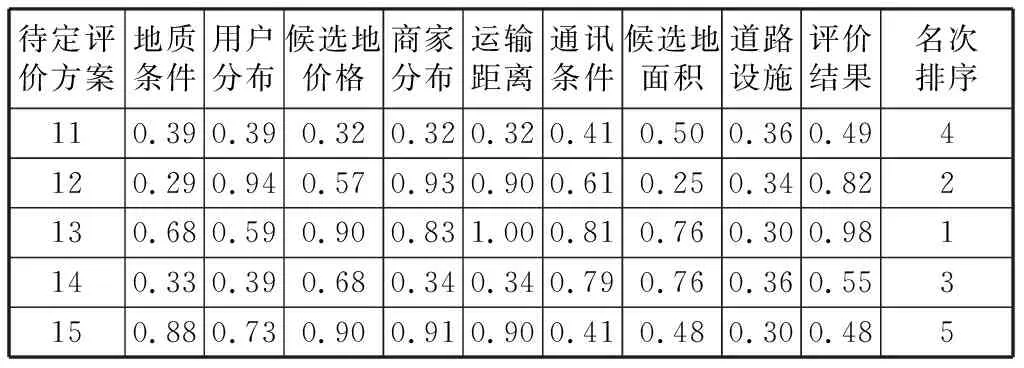
表3 评价方案及测试结果

根据图3中的计算结果可以明显地观察出表3中最优最差的方案，最优为方案13，最差为方案15，每一个方案中的指标因素所表达的结果与实验结果基本达到一致，所以可以用于配送中心选址决策。

4 结束语

在实际中配送中心选址远比我们想象的困难，这是一个及其复杂的问题，不同的因素相互制约，相互影响，相互控制。虽然影响的因素很多很复杂，但我们可以使用模糊神经网络方法来解决，对于非线性关系问题一般可以使用模糊神经方法进行处理，要求这种方法要保证定性因素的量化以及大量的数据，并对其进行一定程度的训练。