一类Kirchhoff型方程组极小能量解的存在性

孙宜民

(西北大学 数学学院, 陕西 西安 710127)

本文研究如下形式的非局部边值问题:

(1)

其中:Ω是RN中具有光滑边界的有界区域；M1，M2：R+→R+以及f,g:Ω×R→R都是连续函数。

由于在方程中含有整个区域上的积分项, 所以这类问题称为非局部问题。事实上,这种形式的非局部算子最早出现在Kirchhoff方程中:

(2)

早在19世纪80年代, Kirchhoff在研究弹性弦自由振动时首次给出了如下方程(见文献 [1]):

(3)

其中ρ,P0,h,E,L均为常数。而方程(2)所刻画的是方程(3)的稳态解所满足的方程。Lions在文献[2]中首次应用变分法研究了Kichhoff型方程 (2)。此后该问题引起了很多知名的数学家的关注, 见文献 [3-10]。此外，下降流不变集方法在半线性椭圆型方程中有非常重要的应用[11]。张志涛与其合作者在文献[12]中利用该方法得到了非局部椭圆型方程(2)的非平凡解。

本文主要考察当f与g是如下特殊形式的非线性项时, 非局部方程组正解的存在性。具体来说, 研究如下形式的方程组的正解:

(4)

关于具有临界非线性项的Kirchhoff型非局部方程组的讨论, 已有的文献较少。 对于单个方程的情形, Alves与其合作者在文献[3]中考察了如下形式的非局部方程

(5)

其中Ω是R3中具的有界光滑区域。他们运用集中列紧原理证明了当参数λ充分大时,方程(5)对应的能量泛函具有紧性, 从而得到该方程极小能量正解的存在性。在此思想的启发下,本文将该结论推广到非局部方程组的情形。

假设非局部项Mi:R+→R+(i=1,2)满足如下条件:存在m0>0以及b≥0,使得对任何t∈R+，以下两式成立

Mi(t)≥m0，

(6)

(7)

相比已有文献中关于非局部项的限定条件, 本文给出的条件(6)和(7)更广并且由条件(7)可知, 对任何t≥0,存在K>0，满足

1 主要结果

本文的主要结论如下。

定理1假设10,方程组(4)至少存在一个具有极小能量的正解。

记号说明:

2 定理的证明

方程组(4)的正解恰为如下方程组的解:

(8)

该方程组对应的能量泛函为:

首先，证明该泛函具有山路几何结构。

引理1对任何β>0，存在δ>0，α>0以及e∈H，满足

(i) 当u∈H时,‖u‖≥δ,Φ(u)≥α>0;

(ii) ‖e‖>δ,Φ(e)<0。

证明由Sobolev嵌入定理, 存在C>0，使得对任何u∈H

(9)

因而

由于10，满足

(10)

令

(11)

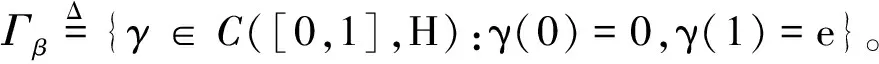
引理2在定理1的条件下, 当β→∞时,c*(β)→0。

证明利用引理1, 存在tβ>0，使得Φ(tβφ,tβφ)=maxt≥0Φ(tφ,tφ)。因而

(12)

这表明tβ与βtβ关于β均一致有界。

不妨设当β→∞时，tβ→0。对任何t∈[0,1]，令γβ(t):=te(β)，则γβ∈Γβ。

结合式(12)可知，0≤c*(β)≤Kt2q‖φ‖2q。因此当β→∞时，c*(β)→0，证毕。

利用山路引理(见文献[13]),可知存在{un=(un,1,un,2)}⊂H，满足

Φ(un)→c*(β),Φ′(un)→0。

假设(un, 1,un, 2)是非负的, 若不然, 考虑(|un,1|,|un,2|)。对于充分大n，

c*(β)+‖un,1‖+‖un,2‖≥

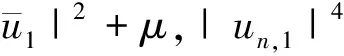
集中紧原理(文献[14]引理1.2)表明存在至多可数指标集Λ，序列{xi}⊂R4以及{μi},{νi}⊂[0,∞),满足对任何i∈Λ，下式成立

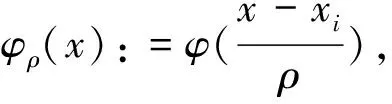
利用文献[11]中的证明思想, 不难证明当β充分大时Λ是空集。从而有在空间L4(Ω)中

由Fatou引理可知

从而有

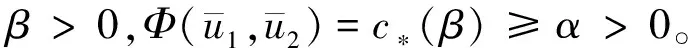
定理1的证明

(13)

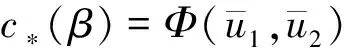
3 结 语

本文研究了一类具有临界非线性项的Kirchhoff型方程组, 运用变分法、集中列紧原理、极大值原理、山路引理等工具, 证明了该方程组极小能量解的存在性。从而将文献[3]的结果推广至方程组的情形。