纳米多孔结构气凝胶传热模型及绝热机理研究

, , , ,

(石家庄铁道大学 材料科学与工程学院，河北 石家庄 050043)

陈一泊,张光磊,贾伟韬,等.纳米多孔结构气凝胶传热模型及绝热机理研究[J].石家庄铁道大学学报:自然科学版,2018,31(4):83-87.

气凝胶是一种具有空间网络骨架且结构可控的轻质纳米多孔隔热材料，具有高比表面积，高孔隙率，低密度，低介电常数和优异的隔热性能[1]，在建筑节能、生物医用、航空航天等领域具有广泛的应用前景[2-4]。气凝胶内部热量传递的形式主要分为3种：传导传热、对流传热以及辐射传热，其孔径尺寸和固相结构的特征尺寸都属于纳米级，因此在传热方面具有显著的纳米尺度效应[5]。从气凝胶的微观结构出发,研究其传热特性进一步分析骨架结构内部的传热机理，可以将气凝胶材料更好地应用在各个领域。

气凝胶的三维网状骨架结构导致其传热过程相对复杂，近年来，国内外许多研究者通过理论模型来简化气凝胶的微观结构研究其传热过程。Zengetal[6]提出了3种立方阵列结构的气凝胶理想单元模型，分别为交叉方杆、交叉圆杆及由小球体构成的立方阵列单元模型。Weietal[7-8]和Luetal[9]均采用纳米球体构成的立方单元模型来表征气凝胶基体材料的纳米多孔结构。施一长[10]建立了四棱柱、六棱柱和八棱柱3种纳米孔结构模型，气凝胶密度较小时，四棱柱计算结果与实际值更吻合。Xieetal[11]在此基础上提出了一种交叉分形球杆单元模型，推导出气凝胶及掺入添加剂复合材料的整体有效热导率表达式。

建立基于气凝胶单元体结构的传热模型，综合考虑了气凝胶颗粒的气固耦合热传导、纳米颗粒堆积所构成孔隙中的气相热传导及辐射传热，推导出有效热导率计算表达式,并进一步研究结构参数对SiO2气凝胶及纤维复合气凝胶等效热导率的变化关系，最终揭示了气凝胶纳米多孔结构内部的传热机理。

1 气凝胶传热模型

将气凝胶的整个骨架结构简化为具有直径d的球形纳米孔在整个空间呈周期性无限规则排列，如图1(a)所示。可从中抽取如图1(b)的单元体模型，将其等价为边长a的立方体结构单元，孔洞直径为d。简化的单元体结构模型的固相是由具有开放性孔隙结构的气凝胶纳米颗粒组成，从而进一步将含有纳米孔结构的气凝胶颗粒简化为球体立方阵列结构模型，如图1(c)，而整个骨架结构中的孔隙由空气来填充。

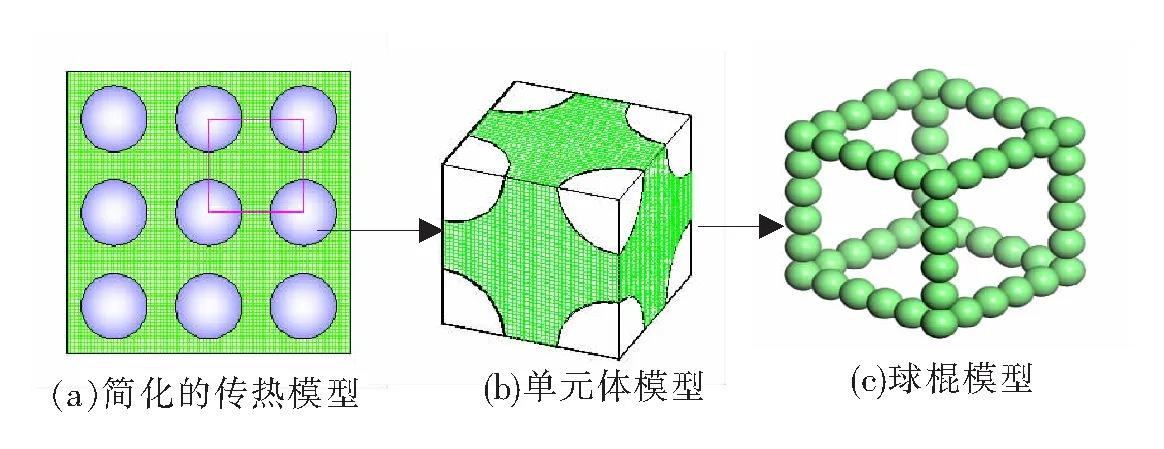
图1 气凝胶简化传热模型

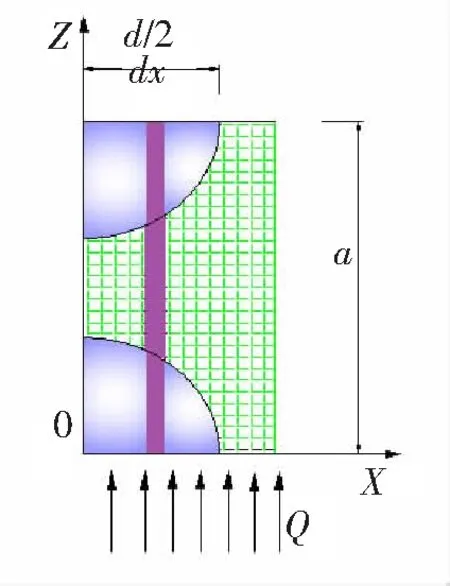
图2 传热分析图

1.1 单元体模型的气固耦合热导率

假设结构单元体内部的传热为一维稳态传热过程，依据单元体结构模型的对称性，可将单元体结构看作是由4个高为a的1/4柱体结构所组成，而每部分柱体结构包含纳米孔结构和固相结构，如图2所示。假设通过单元体的温差为ΔT，通过单元体结构模型传递的总热量为Q，包含2部分：Q1为通过球形孔内的气相及孔洞之间连接固相部分传递的气固耦合热量；Q2为通过柱体结构的边缘固相传递的热量。

由于其传热过程为一维稳态传热，根据傅里叶定律，可以推导出Q1、Q2的计算公式如下

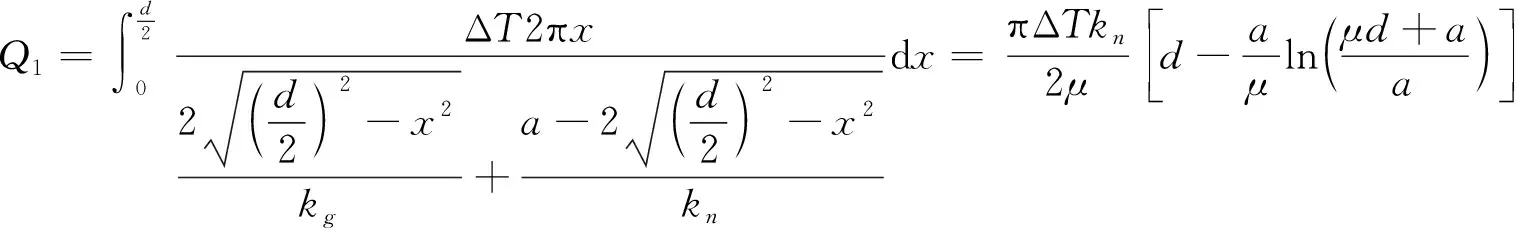
(1)

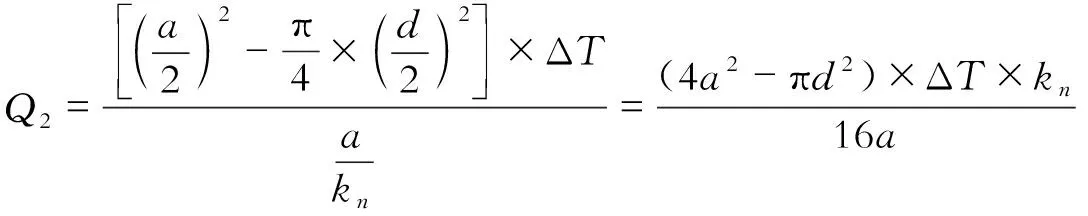
(2)

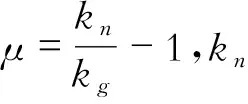
(3)

1.1.1 气凝胶纳米颗粒的热导率

简化的气凝胶传热计算模型的固相是由具有纳米孔结构的气凝胶颗粒组成，将气凝胶纳米颗粒简化为小球体构成的立方阵列结构模型，则气凝胶纳米颗粒的气固耦合热导率可以表示为[12]

(4)

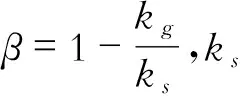
1.1.2 气相热导率

1969年Kaganer[13]基于一组平行板间的气体碰撞理论，将两平行板间的距离假设为孔径尺寸，提出了与孔径尺寸相关[14]的气相热导率公式

(5)

式中，kg,0为气体在自由空间下的热导率；ε为气凝胶的孔隙率；P为气体压力；ds为颗粒直径。

1.2 辐射传热

纯气凝胶在高温下对小于8 μm的近红外辐射几乎透明，抑制高温辐射能力较弱，随着温度逐渐升高，辐射传热成为热传导的主要方式，隔热性能逐渐降低[15]。将气凝胶假设为光学厚介质，采用Rossland扩散近似[16]计算辐射热传导，进一步得出辐射热导率表达式[17]

(6)

式中，n为遮光系数，对于气凝胶约为1；σ为Boitzman常数，σ=5.67×10-8W/(m2·K4)；e为平均衰减系数，对于气凝胶约为22.7 m2/kg。

2 热导率计算与模型验证

气凝胶的等效热导率为气固耦合热导率与辐射热导率之和，将上述传热模型的计算结果与实验数据进行对比可知，当δ=0.25，固相热导率ks=0.36 W/(m·K)时，模型计算结果与实验数据差值较小。在计算模型的过程中，气凝胶球形纳米颗粒的接触参数a2=0.85[8]保持不变，球形颗粒直径在2～5 nm范围内取值，气凝胶纳米颗粒组成的孔洞在9～16 nm范围内取值。

图3为300 K时不同密度下气凝胶热导率的理论计算结果与实验值对比图。从图3中可以看出，Wei et al[8]提出的模型计算结果值略低于实验数据，而本模型提高了计算精度。在相同温度下，随气凝胶密度的增加热导率呈先逐渐减小后递增的趋势。当气凝胶的密度较小时，其孔洞较多，此时随密度增加固相导热逐渐增强，但固相导热对有效导热系数所做贡献仍低于气相导热，因此单元体模型的有效热导率随之减小；随着密度继续增大，孔隙率降低，当密度增大到某一值时，此时固相导热主导了单元体模型的传热，则单元体模型的导热系数将随密度的增大逐渐升高。

图4为气凝胶热导率随温度的变化关系与实验结果对比图。由图4可知，当温度低于450 K时，该单元体传热模型的计算结果与实验值较为接近；当温度高于450 K时，实验结果略高于该单元体结构模型的计算结果。当气凝胶密度一定时，辐射热导率与温度的三次方成正比关系，对有效热导率所做贡献随温度升高将逐渐增大。而真实气凝胶的内部结构存在部分尺寸较大的孔径，这些孔径在高温下透光性较好，导致其隔热性能略差，因此在高温下该单元结构模型的计算值略低于实验值。

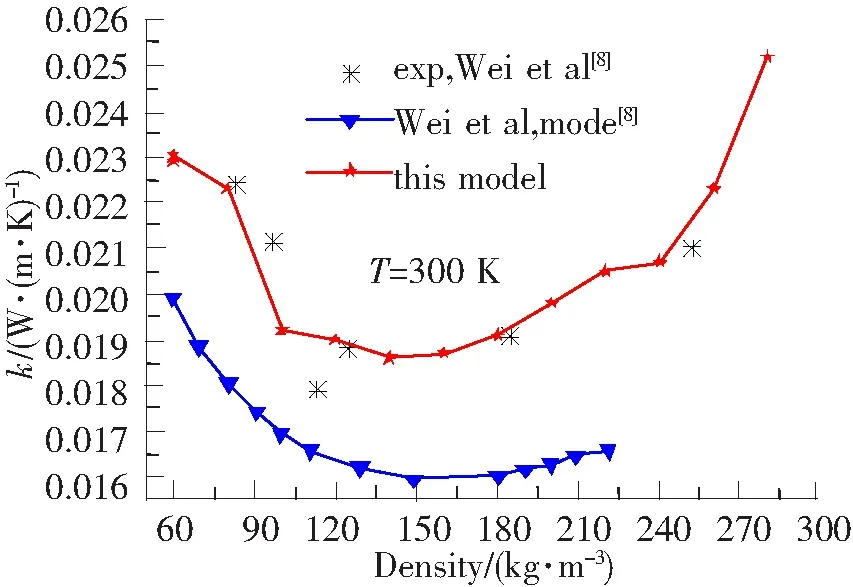
图3 不同密度下气凝胶热导率的计算结果与实验值对比图

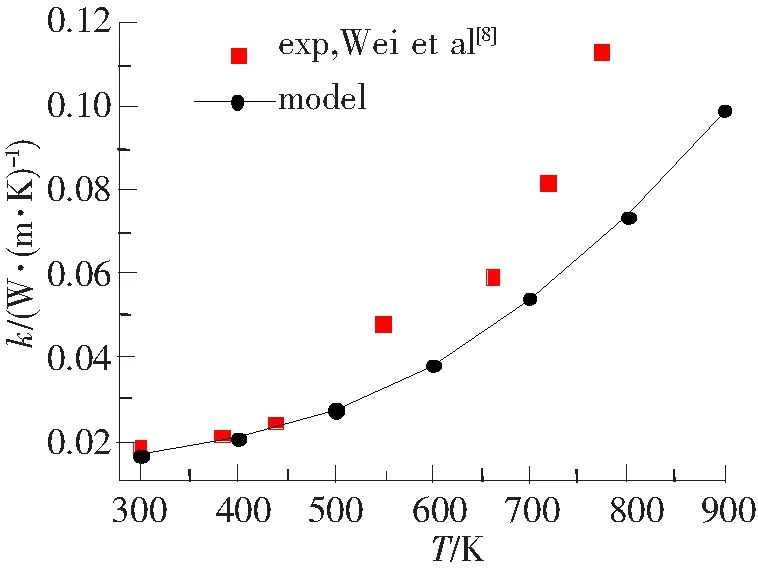
图4 不同温度下气凝胶热导率的计算结果与实验值对比图

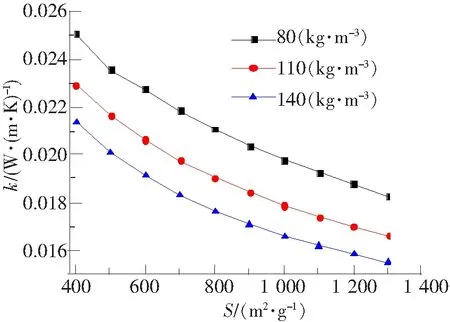
图5 气凝胶导热系数随比表面积的变化关系曲线

不同密度下气凝胶导热系数随比表面积的变化关系曲线如图5所示，单元体结构模型的热导率随比表面积的增大呈逐渐减小的趋势。主要是由于气凝胶纳米颗粒所形成的孔径随比表面积的增大逐渐减小，气体分子的运动将进一步受到约束，因此气相传热所做贡献逐渐降低。并且随比表面积的增大固相骨架结构所做的贡献逐渐增大，将会在一定程度上弥补气相传热能力的降低，因此气凝胶有效导热系数的降低速率逐渐变得缓慢。

3 纤维复合气凝胶热导率计算

对于添加纤维的复合材料热导率计算模型，纤维的引入将改变气凝胶的纳米多孔结构，进而影响各种传热方式。假设纤维随机分布在垂直于热流方向的平面上，采用串联模型[18]计算复合材料的气固耦合热导率，则复合材料的等效热导率整理为

(7)

式中，ke为气凝胶的气固耦合热导率；kf为纤维的热导率；φf为添加的纤维的体积分数；βt为复合材料的消光系数。

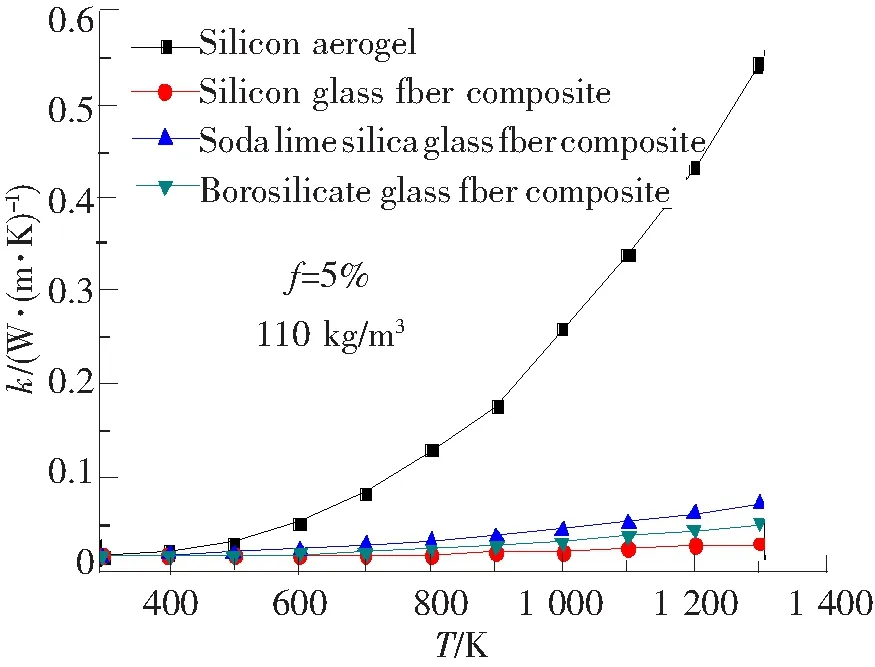
图6 纤维复合气凝胶热导率随温度的变化曲线

SiO2气凝胶基体材料的密度为110 kg/m3，掺入纤维的体积分数5%，采用ADT辐射理论计算纤维的消光系数，复合材料的整体消光系数为纤维消光系数与气凝胶有效消光系数之和[19]。纤维—气凝胶复合材料热导率随温度的变化规律如图6所示，在低温下SiO2气凝胶与复合材料热导率相差较小，两者隔热性能的差距随温度升高越来越大。温度为1 300 K时，SiO2气凝胶的热导率从0.541 33 W/(m·K)降到添纤维—气凝胶复合材料的0.030 56～0.052 58 W/(m·K)。4种复合材料中，石英纤维—气凝胶导热系数最小。

3种不同纤维的气凝胶复合材料综合热导率随纤维体积分数变化结果如图7所示。从图7中可以看出，两种温度下，气凝胶复合材料的有效导热系数随纤维体积分数的增加均明显降低，且掺入石英纤维的复合材料隔热性能最好。当纤维掺入量相同时，由于辐射传热随温度升高所占比重增大，复合材料的热导率急剧升高。体积分数为10%时，钠钙玻璃纤维复合材料的热导率从0.021 56 W/(m·K)升高到0.048 23 W/(m·K)。

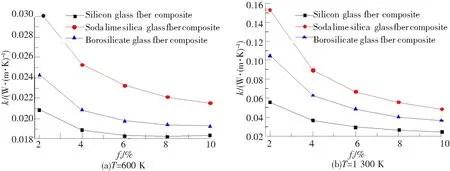
图7 气凝胶复合材料热导率随纤维体积分数的变化关系

4 结论

基于傅里叶定律综合考虑了气凝胶颗粒的气固耦合热传导、纳米颗粒堆积所构成孔隙中的气相热传导及辐射传热。建立了纳米多孔结构气凝胶的传热模型，并将该模型的计算结果与实验结果进行对比验证其合理性。计算了掺加不同体积分数的石英纤维、硼硅酸纤维、钠钙玻璃纤维复合气凝胶在不同温度下的热导率。结果表明，纤维的加入能够有效提高复合材料的隔热性能，且在高温下的抑制效果更明显，在不同温度下石英纤维抑制高温辐射热导率的效果最佳。