异步电机参数辨识系统研究

，

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

0 引言

在基于转子磁场定向的异步电机矢量控制中，由于其转子磁链角计算和电流解耦对电机参数有较高的要求。电机的高性能控制在很大程度上依赖于异步电机本身参数，而异步电机铭牌上不会给出相应的电机参数。因此，对异步电机参数的辨识是一个不容忽视的重点。电机参数辨识方法主要有两种，即离线辨识法和在线辨识法。在线辨识方法可以实时跟随电机不同工况进行校正，能更好地实现电机的自适应控制，但其模型复杂，计算量大，方法应用难度大，对控制单元的运算能力要求很高，目前多数在线参数辨识方法还在理论研究中[1-4]。传统的离线辨识方法需要独立地进行直流、堵转、空载3项实验[5-6]，需要对设备反复拆卸，加装不同种类控制器，操作繁琐，并且在实际工况下，这种情况往往不被允许。

现利用逆变器本身的性能，结合DSP芯片实现SVPWM控制[7]，将3个实验综合设计为一个系统，使异步电机参数辨识更加方便、快捷。同时运用最小二乘法、离散傅里叶变换[8]，使得辨识过程更加简单，辨识结果更加精确。

1 电机辨识原理

图1 异步电机稳态时单相T型等效电路

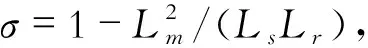
电机试验中利用SVPWM技术产生电压矢量，辅助参数辨识实验的进行。异步电机驱动电路[9-10]如图2所示，主要由6个功率开关管元件组成，利用其8种工作状态来合成电压矢量。

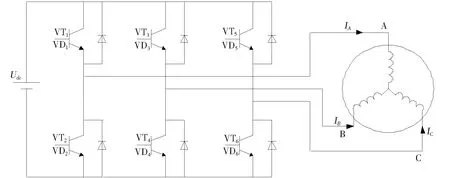
图2 异步电机驱动主电路

1.1 定子电阻参数辨识

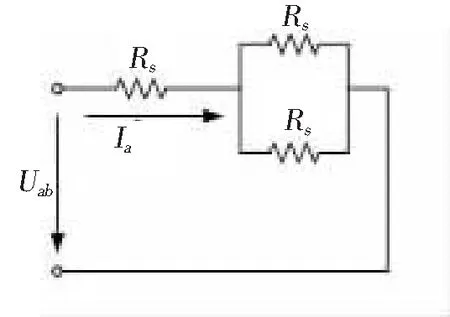
图3 直流实验等效电路

采用直流实验进行定子辨识，通过控制逆变器对电机施加低压直流电，根据欧姆定律计算出电阻值。利用SVPWM技术对母线电压Udc进行斩波，产生高频电压脉冲，近似直流电。对于异步电机而言，此时B相定子电阻与C相定子电阻并联后，与A相定子电阻串联，此时等效电路图如图3所示。因此母线电压即为相电压Uab，A相线电流即为Ia。

电机的定子电阻为

Rs=Uab/(1.5Ia)

(1)

在矢量控制的坐标变换中，根据α-β坐标系下的电压、电流与三相电压、电流的关系，得到SVPWM的输入给定为

(2)

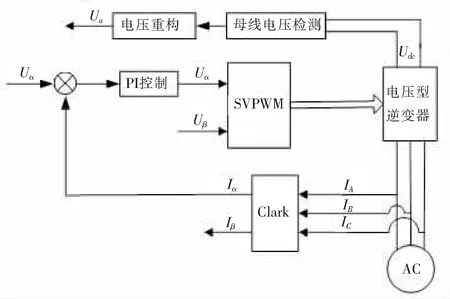
图4 直流实验控制结构图

为保证电流的稳定，防止电压过大，实验采用电流的PI控制，其控制结构如图4所示，给定α轴恒定的电流值，通过反馈定子电流，进行PI控制。并采用了电压重构技术，检测母线电压和计算PWM占空比，计算出电机相电压Uab，利用霍尔传感器测得其线电流Ia。

在直流实验中，电压与电流之间存在y=ax+b的线性关系，其中，y为相电压Uab，x为线电流Ia，a为电阻Rs，b为此线性相关参数[8]。由于测量精度的问题，电压和电流在测量过程中容易产生误差，导致计算出的电阻结果不准确。在实验中采用同一条件下多次测量的方法，来减小测量过程中误差带来的影响。测出n组数据xi，yi(i=1，2，…，n)值，根据最小二乘法的原理，未知参数a、b的求取应该满足式(3)取最小值。

(3)

使式(3)取极小值条件为

(4)

整理式(4)得

(5)

解方程得

(6)

其中

(7)

把所测得的数据代入式(5)就可以求出a，b的值。采用简单的最小二乘法处理数据，其公式简单、运算量小，同时也能够保证结果的精确性。实验证明采用最小二乘法处理数据对解决工程问题而言，是一种非常简单、实用、有效的方法。

1.2 转子电阻、电感参数辨识

图5 堵转实验等效电路

采用堵转实验进行转子电阻、漏感的辨识。其原理是给电机绕组接入单相正弦交流电，此时电机处于堵转状态，不会产生转矩。当电压频率较高时，由于励磁电感很大，图1中流过励磁回路的电流可以忽略不计，转差率s=1。此时三相电机内部电路可以等效为B相、C相电阻并联，后与A相电阻串联；B相、C相漏感并联，后与A相漏感串联。其等效电路图如图5所示。

等效阻抗为

Z=Uab/Ia

(8)

等效电阻为

R=(Uab/Ia)cosθ

(9)

等效电抗为

X=(Uab/Ia)sinθ

(10)

定子、转子漏感为

σLs=σLr=X/(3ω)

(11)

式中，ω为电压基波角频率。

转子电阻为

Rr=(2/3)R-Rs

(12)

在SVPWM 控制算法中，控制Uα输入单相正弦电压，且Uβ=0，保证B、C两相桥臂控制信号相同。当电流稳定后，得到异步电机A相电流以及线电压Uab，进行离散傅里叶变换，可以得到相应的基波有效值和功率因数角。

由于电压和电流都是正弦波且它们之间存在相位差，其相位差即为功率因数角，可以利用电流为零时取电压值的方法，获得其电压值再除以其幅值再进行反正弦操作，就能够得到功率因数角，进而得到功率因数cosφ，大大简化了功率因数的计算过程[11]，得到

(13)

式中，U为A相电流为零时的相电压Uab，M为相电压的幅值。

根据式(8)～式(12)就可以推算出转子电阻Rr和定子、转子漏感σLs、σLr。

1.3 励磁电感辨识

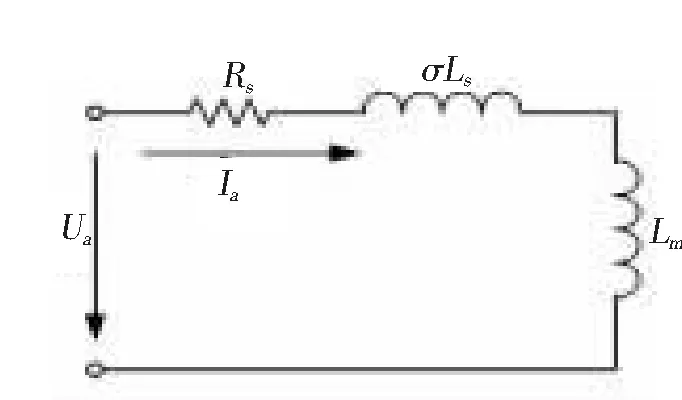
图6 空载实验等效电路

采用空载实验进行励磁电感辨识，其原理是电机空载运行时转速接近同步转速，转差率s接近于零，电机转子回路可以近似为开路，等效电路如图6所示。

图中等效阻抗为

Z=Ua/Ia

(14)

等效电抗为

X=(Ua/Ia)sinθ

(15)

励磁电感为

Lm=X/2πf-σLs

(16)

通过电机开环V/F控制，施加额定频率的交流电压，使异步电机达到额定转速。通过霍尔传感器得到其母线电压和A相电流，利用电压重构技术即可得到Uab。采用离散傅里叶变换计算出电压、电流的基波有效值和功率因数角。再根据式(14)～式(16)即可计算出励磁电感Lm。

2 辨识结果

图7 系统流程图

采用TI公司的DSP芯片TMS320F2812作为主控器，采用专用驱动芯片IR2110和高达25 A，1 200 V的IGBT管，PWM驱动信号通过高速光耦完全隔离高压与低压侧，保证驱动板不受高压干扰。用霍尔传感器检测输出电流波形，使低压侧和高压侧完全隔离。

实验中使用的电机额定参数为：Pn=200 W；Un=36 V；In=9 A；wn=1 400 r/min；极对数P=2。SVPWM载波频率10 kHz，死区时间为3.2 μs，IGBT最大开关延迟时间Ton=0.1 μs，Toff=0.3 μs。为了实现电机参数辨识目标，基于DSP编写了电机参数辨识系统，系统流程如图7所示。

图8所示为直流实验电压电流，在直流试验中，待电流稳定后，通过DSP的ADC模块进行转换，以50 Hz的频率对电压和电流进行同步采样，得到128个点的电压和电流值，并用最小二乘法计算，获得定子电阻Rs。

在堵转试验中，通入30 Hz单相交流电，电流和电压的采样周期为260 μs，这样采集128个点即为一个完整周期。图9为堵转实验电压、电流，从图中可以看出电压超前电流，电压和电流近似正弦波。

图8 直流实验电压电流

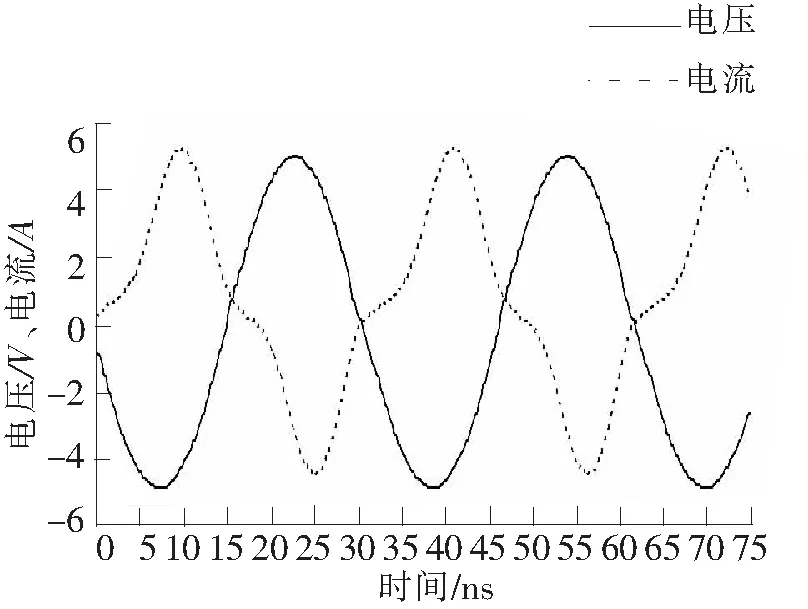
图9 堵转实验电压电流

图10 空载实验电压电流

在空载实验中，通入50 Hz三相交流电，得到电压电流波形如图10所示。电机运行稳定后进行采样，由于50 Hz三相交流电，周期为20 ms，对其电压和电流进行同步采样，采样128个点，采样周期为156 μs，保证了采样点为一个完整周期，方便进行离散傅里叶变换。

所得到的辨识结果如表1所示，通过计算得到转子时间常数为Tr=0.017 1，与之前通过矢量控制得到的Tr=0.017 4对比，误差为1.72%，具有较高的准确性。

表1 辨识结果

3 结语

电机参数的准确性对电机的矢量控制有着重要的影响。本文基于空间矢量调制技术(SVPWM)，采用了PI电流控制和最小二乘法，准确地计算出定子电阻。在堵转、空载试验中采用离散傅里叶变换数据处理手段，去除了其它谐波的影响，获得了准确的电机参数。研究的异步电机辨识系统，方法简单、程序运行时间短，其参数的准确性，能够满足矢量控制的需求。