捷联式制导迫弹末制导弹道优化设计*
杨智刚,孙瑞胜,朱 斌
(南京理工大学,南京 210094)
0 引言
为了充分发挥捷联式制导迫弹制导控制组件的优势,对捷联式制导迫弹进行弹道优化具有重要的理论研究意义和工程应用价值。捷联式制导迫弹弹道优化问题是具有严格过程约束和终端约束的最优控制问题[1]。解决这类问题的方法通常分为直接法和间接法[2],文献[3]采用极小值原理与自适应进化粒子群相结合的方法,对航空时敏制导炸弹增程弹道进行组合优化设计。文中在此基础上进行改进,最终在解决复杂的非线性最优控制问题时,快速找出最优解。
近年来,制导迫弹以其高命中精度、低后勤保障成本等优点受到广泛关注[4-6],但其研究内容主要集中在气动特性分析[7]、脉冲力控制建模与仿真[8-9]等,关于制导迫弹弹道优化设计的文献较少。文献[10]对制导迫弹初始状态的发射角进行优化,提高了命中概率,但没有考虑飞行过程中状态量的优化。文献[11]建立了制导迫弹捷联激光导引头的数学模型,得出了以无控弹落点为目标点进行弹道设计可以提高制导精度的理论结果。文献[12]基于卫星/激光半主动复合制导迫弹,分析了舵偏角和起控时间对制导迫弹最大修正能力的影响,初步验证了末端采用激光制导的可行性。为此,文中以捷联式制导迫弹为研究对象,采用改进的粒子群优化算法,以制导迫弹的飞行攻角和飞行时间为优化变量,选取捷联导引头的部分技术指标作为约束条件,对目标进入制导迫弹视场时的最大弹道高度进行优化设计。
1 优化问题描述
1.1 捷联式制导迫弹工作过程
捷联式制导迫弹的工作过程由三个阶段组成,第一阶段为制导迫弹以一定初速和射角发射后,按自然弹道飞行;第二阶段为制导迫弹飞过弹道顶点,捷联导引头开始工作,对地面目标进行探测;第三阶段为制导迫弹下落一定高度到点A时,目标进入捷联导引头视场内,制导迫弹操纵机构开始工作,控制迫弹命中目标。工作过程如图1所示,文中针对第二阶段和第三阶段的飞行攻角和飞行时间进行优化。

图1 制导迫弹工作过程
1.2 飞行动力学模型
为便于研究,在制导迫弹初步设计阶段,可以假设地球表面为平面,不考虑地球自转的影响,在纵向平面内建立制导迫弹动力学模型。
(1)
其中:m为质量;V为速度;θ为弹道倾角;ωz为俯仰角速度;Jz为转动惯量;ϑ为俯仰角;X为阻力;Y为升力;Mz为俯仰力矩;ε(α*,T)为控制方程;其余符号具体意义详见文献[13]。
1.3 捷联导引头建模
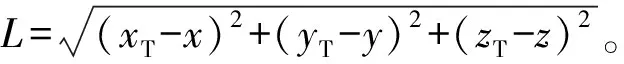
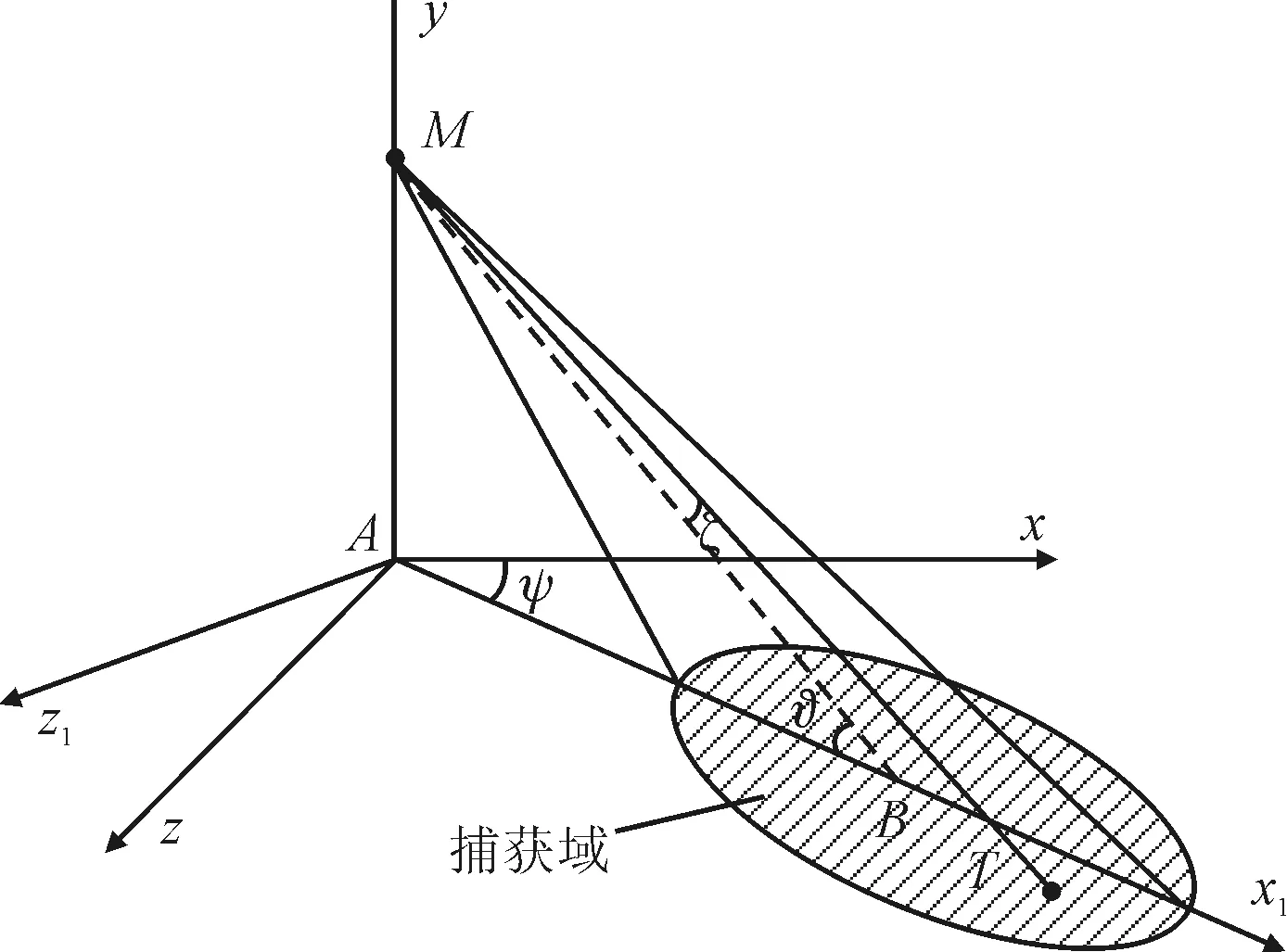
图2 捷联导引头空间视场示意图
1.4 约束条件
1)初始状态约束:制导迫弹初始发射条件为v(0)=v0,x(0)=x0,y(0)=y0,θ(0)=θ0;
2)终端状态约束:tf为弹道优化的结束时间,θmin≤θ(tf)≤θmax,脱靶量Δx≤ΔxCEP;
3)过程状态约束:在捷联导引头成功捕获目标后,需要保证目标一直处于捷联导引头的视场内,因此根据捷联导引头技术参数,弹目距离需要满足约束L(t)≤Lmax,跟踪误差角ζ需要满足约束ζ(t)≤ζmax;
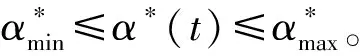
1.5 目标函数
为了提高捷联导引头在末制导段的目标捕获概率,制导迫弹总体设计初步阶段的重要途径是令捷联导引头尽可能早地探测到目标。因此,选取捷联导引头探测到目标时的弹道高度作为目标函数,即:
maxJ=y|ζ=ζmax
(2)
为了提高弹道优化的计算效率,文中引入罚函数P(t)将带约束问题转化为无约束问题进行求解。当上述约束条件不能被满足时,P(t)将取负值对目标函数进行惩罚,即:
maxJ=y|ζ=ζmax+μP(t)
(3)
其中μ为惩罚因子。
2 粒子群优化算法
2.1 优化变量离散化

2.2 改进的粒子群优化算法
粒子群优化算法是一类模仿鸟群觅食的智能优化算法。在N维搜索空间中随机生成一个包含M个微粒的种群,种群中每个微粒拥有一个表示优化问题解的位置向量Xi=(xi1,xi2,…,xiN),根据位置向量计算出目标函数的值来判断该微粒的优劣;位置向量Pi=(pi1,pi2,…,piN)用来记录每个微粒在搜索空间中全局最优位置;速度向量Vi=(vi1,vi2,…,viN)表示微粒在搜索空间中的飞行速度;pbest表示微粒的局部最优位置,gbest表示种群的全局最优位置。微粒的速度和位置的更新公式如下[14]:
(4)
(5)
其中:d=1,2,…,N;k为迭代次数;r1、r2为[0,1]区间均匀分布的随机数;c1、c2分别为认知参数和社会参数;w为惯性权重。
为了提高微粒在误差范围内的局部收敛速度,文中采用线性递减惯性权重[15]的粒子群算法。粒子群算法的基本流程如下:
1)初始化搜索空间、种群大小、最大迭代次数、惯性权重、速度限制等;
2)更新微粒的位置和速度;
3)根据粒子的位置计算优化变量α*和T;
4)将优化变量α*和T代入弹道模型解算;
5)计算目标函数J,更新局部最优目标函数值和全局最优目标函数值;
6)如果满足停止条件,则停止计算,输出全局最优位置和目标函数值;否则,根据局部和全局的最优目标函数值调整微粒的速度和位置,返回步骤2)。
3 仿真分析
捷联式制导迫弹的初始弹道计算条件为:m0=15 kg,v0=320 m/s,x0=0 m,y0=0 m,ωz0=0 rad/s,θ0=45°,ϑ=45°,目标位置坐标为(xT,yT,zT)=(5 500 m,0,0)。
制导迫弹按自然弹道飞过弹道顶点后开始对弹道进行优化,粒子群算法的参数为:种群大小M=80,认知参数和社会参数c1=c2=1.8,惯性权重w从1.0线性递减到0.4,最大迭代次数取100次,约束条件为:θmin=-60°,θmax=-45°,ΔxCEP=5 m,Lmax=2 000 m,ζmax=7.5°,Tmin=0 s,Tmax=0.5 s,αmin=-5°,αmax=5°。
根据上述仿真参数,进行弹道优化仿真。图3~图8为弹道参数对比曲线,其中自然弹道表示捷联式制导迫弹无控自由飞行的弹道仿真结果,优化弹道表示按粒子群算法求得的最优弹道仿真结果。
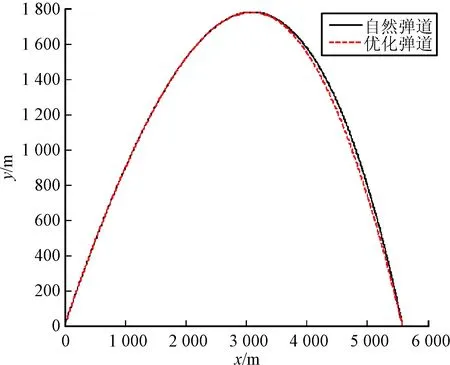
图3 弹道对比曲线
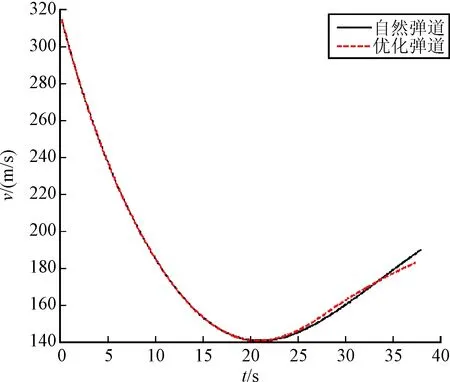
图4 速度对比曲线
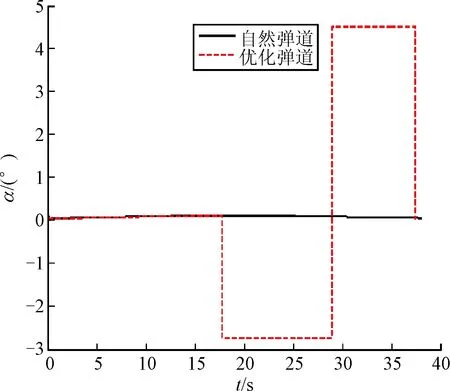
图5 攻角对比曲线
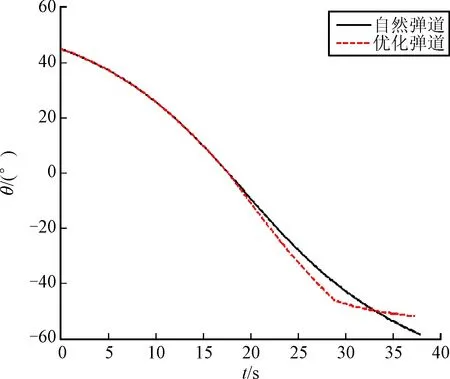
图6 弹道倾角对比曲线
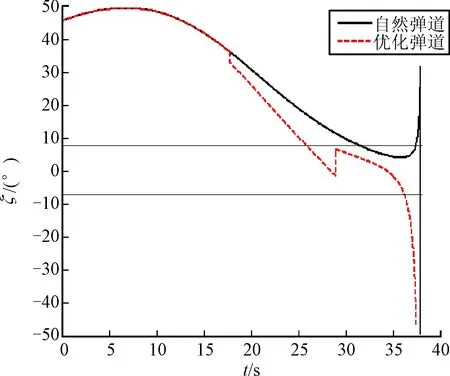
图7 跟踪误差角对比曲线
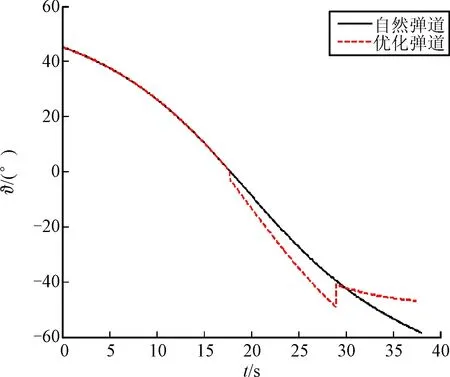
图8 俯仰角对比曲线
由仿真结果可以看出,制导迫弹按优化攻角飞行,捷联导引头能够在较高的弹道高度较早地探测到目标,且探测到目标后的各项弹道参数均满足约束条件。由图5可以看出,制导迫弹在末制导段先以负攻角飞行,负的攻角指令可以令制导迫弹产生低头的力矩,这样有利于捷联导引头尽早地探测到目标,但会导致射程减小,因此再以较大的正攻角飞行来修正偏差减小脱靶量。

表1 弹道参数对比
图7为捷联导引头光轴线与弹目连线的夹角在纵向平面内的投影,由于捷联导引头在弹道末段进入盲区,且存在一定的脱靶量,因此跟踪误差角ζ在末段发散,当-7.5°≤ζ≤7.5°时,捷联导引头捕获目标,优化弹道明显在自然弹道之前捕获目标。
4 结论
1)针对捷联式制导迫弹弹道优化问题,推导了空间内捷联导引头光轴线与弹目连线夹角的公式,将捷联导引头的技术参数作为约束条件加入到优化问题中,将飞行攻角和飞行时间作为优化设计变量。仿真结果表明,该优化模型是合理的。
2)为了加快粒子群优化算法的收敛速度,文中采用了递减惯性权重的粒子群算法,以目标进入捷联导引头视场内时的弹道高度为目标函数,并引入罚函数,对捷联式制导迫弹多约束弹道进行了优化设计。仿真结果表明,改进的粒子群算法能够较快的计算出最优飞行攻角,捷联导引头能够较早的探测到目标,为制导迫弹末制导阶段提供充足的时间,提高了捷联导引头的捕获概率和制导迫弹的命中精度。文中的研究结果可为捷联式制导迫弹总体设计提供设计依据。

