多移动机器人系统协调控制算法设计
查延麟
(1.中国科学院上海微系统与信息技术研究所,上海200050;2.上海科技大学信息学院,上海201210;3.中国科学院大学北京100049)
随着机器人技术的快速发展,移动机器人控制和路劲规划问题是当前的热门研究方向之一[1-3]。同时,多移动机器人协作控制问题也逐渐引起了越来越多学者的关注[4-6]。当前已经有很多方法可以实现对此类系统的控制[7-8],其中,分布式模型预测控制(Distributed Model Predictive Control,DMPC)是一个热门的研究方向[9-11]。通过对每个子系统未来状态的预测并进行规划,分布式模型预测控制方法得以在不引发机器人之间的冲突的前提下,引导每个机器人完成各自指定的任务。
为了协调多个机器人,机器人之间需要进行通信以避免冲突,而潜在的通信延迟和数据包丢失会导致包括机器人碰撞在内的恶劣后果[13-14]。为了处理这类问题,文献[15]提出了一种量化通信方案。这个方案通过把通信信息量化为整数,以降低信息准确度为代价降低了传输负载。除此之外,机器人系统中存在的其他不确定因素也需要被纳入考虑。一类被称为集合计算的方法可以实现对系统不确定性的建模和处理[16-17]。
文中结合量化通信和集合计算方法,提出了基于DMPC的鲁棒多机器人协调方案。这一方法不仅降低了传输负载,同时通过把包括网络延迟,传感器测量噪声在内的不确定因素纳入了考虑,保证了多移动机器人系统的鲁棒性。
1 问题描述
本文考虑如下由p个移动机器人构成的多机器人系统,每个机器人的动力方程记作
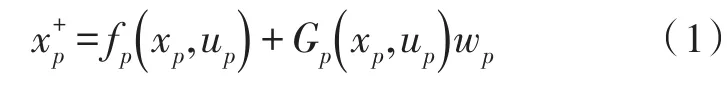
这里xp∈XXp表示机器人的状态量;up∈UUp表示机器人的控制量;wp∈WWp表示机器人的不确定参数;fp:Xp×UUp→XXp以及Gp:Xp×UUp→XXp×WWp为李普希茨连续(Lipschitz-continuous)函数;集合Xp∈ℝnx,Up∈ℝnu,Wp∈ℝnw分别表示机器人可能的状态集、控制集、以及不确定集;nx,nu,nw分别为状态量,控制量和不确定量的维数。
我们把机器人前k时刻的状态序列记作xp(∙)=(xp(0),…,xp(k)),把控制序列记做up(∙)=(up(1),…,up(k)),以及不确定参数序列记做wp(∙)=(wp(1),…,wp(k))。同时,为了研究最糟参数情况下的系统行为,我们定义,对于给定初始状态和控制序列up(∙),机器人在第n时刻所有可能的系统状态构成可达集Xp⊆XXp:

除此之外,我们还假设每个机器人都可以在任何一个系统状态下被停下来,即:

以及所有的机器人都在共同的物理空间中运动,这样每个机器人的状态量之间都存在有耦合约束条件。为了避免违背这些约束条件,实现整个多机器人系统的协调工作,我们采用分布式模型预测控制策略,来对整个多机器人系统进行规划和控制。
具体而言,我们考虑以下鲁棒分布式模型预测控制问题


其中目标函数lp:XXp×UUp→ℝ正定且满足

本文的目标是结合区间算术去计算Xp,以及利用量化通信方法以较低的传输负载获取Cp,设计针对多移动机器人系统的鲁棒分布式模型预测控制算法,来实现对这一系统的协调控制。
2 区间算术
为了求解鲁棒模型预测控制问题(1),我们利用区间算术(Interval Arithmetic,IA)方法计算可达集Xp。区间算术是定义在区间集合II⊆ XX上的一元或二元运算。对于区间集合II的元素,其中上界和下界满足,它们把这一区间参数化成为两个系数,我们用表示区间X。两个区间X,Y之间的加法被闵可夫斯基和定义为:

即Z=X+Y被自然地定义为:

并且相应地,负区间-X被定义为:

并导出减法Z=X-Y为:

类似地,乘法Z=X×Y被定义为

以及除法

当且仅当0∉Y。
由此,如式(4)~(7)所示,区间之间的四则运算被自然地定义为其参数之间的运算。此外,基本初等函数(幂、指、对、三角函数)也可以被扩展到区间集合上,详见文献[16]。
由于初等函数是由基本初等函数和四则运算的有限次复合得到,因此基于式(4)~(7)所定义的四则运算以及文献[16]中的基本初等函数,区间算术方法可以用来计算或逼近标量值初等函数的值域。
这样,若函数fp,Gp的每一个分量都是初等函数,机器人p的可达集Xp可以由区间算术的方法来迭代地逼近:

3 量化通信
为了降低通信负载,我们引入量化通信方法。具体而言,我们把机器人的状态空间XX网格化。我们定义量化函数q:X→ℕnx,把任意一个物理位置x∈XX映射为它所在的网格索引G∈ℕnx。
利用量化函数q,我们可以定义每个机器人有待广播的信息为:

即每个机器人在时刻n向其他的机器人广播自己未来N步内将要经过的格子及相应的时刻Ip(n)。我们把机器人p所接收到的广播信息:

称为“被预定的格子”。这些“被预定的格子”构成了鲁棒分布式模型预测控制问题(3)中的耦合约束项CP。
利用量化函数,每个机器人在第n步时把预测到未来第k步的可达集Xp(k),k∈{0 ,1,…,N}量化为Xp(k)所占据的全部格子的上下界。并把这上下界和相应的每一个时刻k打包作为广播信息Ip发送给其他机器人,如图1所示。

图1 网格化的可达集
图1实线所围成的区域是机器人p预测的第k步可达集Xp,虚线所围成的区域是由区间算术计算出的对Xp的逼近,深色和全部阴影区域分别是被量化的Xp和,格子(2 ,2)和(1 5 ,8)以及时刻k被打包封装进待广播的数据Ip。
由此可见,利用区间算术和量化通信方法,不仅每个机器人的不确定因素所导致的全部可能结果被作为可达集考虑在内,并且这些可达集被以极低的传输负载广播给其他的机器人。
4 鲁棒分布式模型预测控制算法
结合区间算术和量化通信,我们提出针对多移动机器人系统的鲁棒分布式模型预测控制算法(RobustDistributedModelPredictiveControl,RDMPC),其步骤可总结如下:
1)设定全部p个机器人的可行的初始点;
2)设定预测时间窗N
4)所有机器人依次广播Ip(0);
5)设定当前时刻n=1;
6)每个机器人p依次接收被占据的网格信息ip;
7)利用区间算术和优化问题求解器,每个机器人近似求解鲁棒模型预测控制问题(3),获得控制序列up(∙);
8)每个机器人依次执行up(0),并广播Ip(n);
9)设定当前时刻n=n+1,跳转至步骤6)。
当假设(2)成立,求解问题(3)可以得到至少一个可行解,这一可行解使得机器人维持上一状态不变,由此可以得出,这一算法总能找到可行解。详细证明过程类似于文献[14],它证明了这一算法对于相对应的标称系统(nominal system)的可解性。
5 案例研究:四机器人路口调度
本文考虑平面移动的四机器人的路口调度问题,其中路口区域为Xp≔[-6(m),6(m)]2,控制集和不确定量集分别


以及目标函数:

这里,我们设定预测窗口长度为N=4,网格尺寸c=0.5(m)。
此外,我们设定每个机器人各自的出发点和目标位置如表1所示。

表1 机器人初始位置和目标位置
这一案例的数值仿真由Julia编程语言实现,并采用COBYLA[18]作为优化求解器。仿真结果如图2所示。

图2 四机器人运动路径
在图2中,四条深浅不一带圆点的实线表示4个机器人的运动轨迹,阴影区域表示每个机器人预定的格子。所有被同一个机器人预定的格子构成一个管形区域,包含了这个机器人所有可能的轨迹。从图上我们可以看出,在时刻n=8之前,每个机器人都距离其他机器人较远,不需要考虑避开其他机器人,也就因此分别朝着他们的目标点直线前进;从时刻n=9到时刻n=10,这些机器人在区域的中央部分相遇,部分机器人自发的停下来以让其他的机器人通过。这是由于当预测窗口N不够长,机器人不足以在规划出能直接绕开其他机器人的路径。从时刻n=11以后,全部的4个机器人保持直线运动直到他们接近到目标点附近(在预测窗口之内可以到达目标点),朝向目标点运动并抵达。这里,机器人绕开彼此后,先保持直线运动而不是朝向目标点运动的原因是,因为控制量的约束是,即取|up,1|=|up,2|=0.5(m/s)可以最小化目标函数lp;而随后,当机器人可以在一个预测窗口内到达目标点时,只有朝向目标点运动才能最小化目标函数。由此,这一案例验证了RDMPC算法的有效性。
6 结论
本文针对多机器人协调问题,提出了一种结合了区间算术和量化通信的鲁棒分布式模型预测控制策略。这一方法首先利用区间算数,将每一个机器人不确定因素分别考虑在内,预测每一个机器人所有可能的轨迹,保证了多机器人系统的鲁棒性。其次,利用量化通信,把待传送的机器人位置数据网格化为格子的索引,大大降低了机器人之间的通信负载,并以四机器人路口调度问题为例,验证了RDMPC算法的有效性。

