一种基于STR算法的新表压缩方法
董爱迪 李占山 于海鸿
(吉林大学计算机科学与技术学院 长春 130012) (符号计算与知识工程教育部重点实验室(吉林大学) 长春 130012)
在约束编程中,由于表约束算法可以对任何种类的约束编码,并且表达方式简洁,所以近些年来基于表约束过滤算法被广泛研究和使用,其中STR2[1]和STR3[2]算法是当前主流的表缩减算法.关于表约束的研究,国内学者关注于约束可满足问题中二元问题,其中文献[3]的算法将约束求解与优化技术相结合,提高约束求解效率;李占山等人[4]提出新启发式用于回溯搜索过程.同时为了在表约束上维持高阶相容性,王瑞伟等人[5]提出一种对eSTR算法的优化算法.而由于表约束将关系用表的方式显示出来,内存空间的需求可能会由于参数的增加而出现指数型爆炸,所以为了优化表缩减算法性能,降低约束表的空间消耗并提高广义弧相容(generalised arc consistent, GAC)算法的运行速度,许多用于约束表压缩的算法相继被提出.例如用MDD图来表示约束关系的MDD4R[6]算法,当子图十分复杂且压缩率很高时,在其上维持GAC效果十分显著.同时运用c-tuple在笛卡儿积压缩表上维持GAC的STR2-C算法及STR3-C[7]算法,同样在压缩率较大的benchmark实例上,能取得显著的效果提升.而STR-slice[8]算法则是在分割表上维持GAC的算法,这些改进算法都是用一种更加紧凑的方式来表示约束表,从而提高过滤性能.
在众多成功的表压缩方法中,我们发现:约束表中完全长度集合大小严重大于短支持集合,因此运用短支持方法,利用元组的特性,将原有约束表压缩成短表[9],减少约束元组个数,更加节省空间,同时可以比原始STR算法传播更多的约束,甚至由于内存问题,原始STR算法都不能将这些约束放入内存中.但是当压缩率比较小时(即原约束表中元组很少能被压缩成短约束元组),应用短支持方法的ShortSTR2与STR2算法相比运行速度并没有显著提升.而位操作[10]允许在位向量上并行操作来提高算法运行速度,因此文中提出一种新的表压缩算法STRO(simple tabular reduction optimizaton),结合短支持方法和位操作,保留了短支持方法中可以传播更多结点的优点,辅以位操作并行的优势,与主流算法STR2,ShortSTR2相比,约束表空间压缩程度更好,且运行速度有显著提高;与目前维持GAC效果较好的STRbit算法相比,表压缩率更大,可明显降低空间消耗.
1 背景知识
定义1. 约束网络(constraint network, CN)[11].约束网络CN由一个包含n个变量的集合和一个包含e个约束的集合构成.每个变量x都有一个相关的论域dom(x),其中包含了一个变量x的有限赋值集合.每个约束c都有一个集合scp(c)和一个集合rel(c),其中scp(c)是X的子集,集合内元素是约束c涉及的变量.r表示约束c的元数,在正表约束中,rel(c)是满足约束c的元组的集合.若a∈dom(x)则(x,a)是有效的;若a∉dom(x)则(x,a)是无效的.一个元组τ是(x,a)的支持当且仅当 (x,a)∈τ.τ是有效的当且仅当∀x∈scp(c),都有(x,τ(x))是有效的.
定义2. 短支持(short support)[9].短支持S是一个文字的集合S=(y→2,z→1),其中x∈scp(c),且文字x→v是关于Ds有效的,x在S中仅仅出现一次,并且S的每一个超集都包含一个有效的文字,关于scp(c)中每个变量来说都是一个完全长度支持.
在本文中,我们用完全长度元组来表示短支持,*表示一个不被短支持包含的变量.假设有一个约束c涉及3个变量x,y,z,短支持S=(y→2,z→1),S用完全长度表示为{*,2,1}.压缩算法Greedy-Compress是由Jefferson等人[9]于2013年提出,描述如何将大小为r的完全长度元组,逐步迭代压缩直到不能压缩为止.算法用UsedTuples存储可以被压缩的元组,并用CompTuples存储压缩后的元组,最终将所有可能大小的元组收集起来,完成短支持压缩.
定义3. 广义弧相容GAC[12].一个约束c是弧相容的,当且仅当对每一个x∈scp(c),每个值a∈dom(x)在c中至少存在一个支持.
定义4. 位操作(bit-wise operation)[10].位操作将约束表中元组集构造成位表,用数组来表示约束和域,用数组bit_dom[x]表示变量的域,将变量X域中的每一个值对号入座,但是存放的不是变量值而是0或1.0表示与这个位置对应的值不在变量X的值域中,反之则为1.同时用位向量support来表示约束表中的支持,如果元组τ对值对(x,a)关于约束C是有支持的,那么位向量在位置i的值为1,否则为0.
例1. 一个简单原始约束表如表1所示,其中dom(x)={a,b,c},dom(y)={a,b,c},dom(x)={a,b,c}.每个变量值对应的位向量support值如表2所示.

Table 1 Constraint Table 表1 约束表

Table 2 Value of Bit Support 表2 位支持的对应值
2 STRO算法的思想
STRO算法是结合短支持和位操作得到的简表压缩优化方法,其中位操作受到STRbit算法的启发,沿用了STR的算法框架.主要思想是先将约束表压缩为短表,再将其转化为位表,并在位表上维持GAC.整个算法可以分为3个部分:1)将原约束表压缩成短表;2)在搜索过程中动态删除无效的元组;3)为每个变量值对在当前有效的约束表中寻找支持.
为了实现STRO算法,需用到5种数据结构.
1)support(C,X,a).表示值对(x,a)关于约束c的位支持.
2)support*(C,X,a).表示值对(x,a)关于约束c的位短支持.
3)LAST(C,X,a).记录的是最后一个有效位支持的位置,初始化为support.size-1.
4)DEL(C,X).集合中存放所有从值域中删除但还未更新位表的变量值.
5)VAL(C,X).表示的是元组的有效性,初始时每个位的值均为1.
对于表1的约束表,经过STRO算法的第1步短表压缩后将转变为表3,相应的位短支持support*的计算可以看作2部分,首先计算出原有的位支持support,而当任何一个变量x被压缩后,该变量的值对(x,*)的位支持support等于包含*的元组位置的位值为0,其余为1.在表4中,对于压缩后的(y,*)值对的位支持support=(011111),将相应值对的位支持support和(y,*)值对的位支持support进行按位与计算,从而得到位短支持support*.例如变量值(y,a)的support(y,a)=(110100),与support(y,*)=(011111)进行按位与计算后,得到support*(y,a)=(010100).

Table 3 Constraint Table After Short Table Compression表3 短支持压缩后的约束表
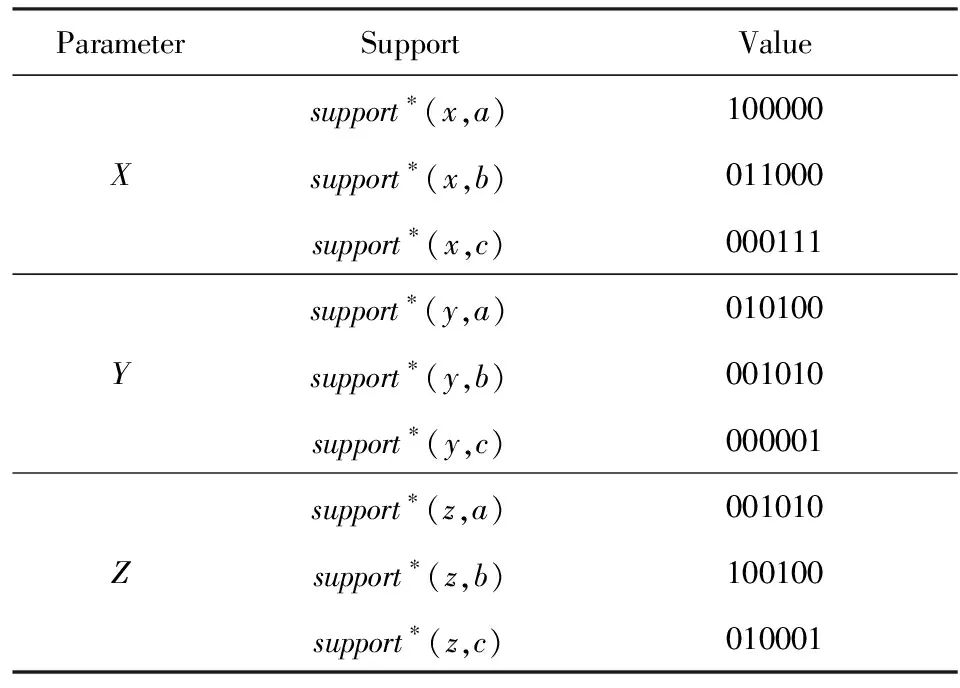
Table 4 Value of Bit Support* After Short Table Compression表4 短支持压缩后的位短支持的对应值
算法1. STRO算法.
Algorithm STRO()
①S←{x|(x→a)∈shorttable∧|dom(x)|>1};
②deleteInvalidTuple();
③ returnsearchSupport();
FunctiondeleteInvalidTuple()
① FOR all variables∈Sdo
② FORa∈DEL(C,X) do
③ FORi≤LAST(C,X,a) do
④u=support*(C,X,a)[i].
mask&VAL(C,X);
⑤ IFu≠0
⑥ save(C,VAL(C,X),restoreV);
⑦VAL(C,X)=(u) &
VAL(C,X);
⑧ ENDIF
⑨ ENDFOR
⑩ ENDFOR
FunctionsearchSupport()
① FOR all variablex∈Sanda∈dom(x) do
②now=LAST(C,X,a);
③ IFsupport(C,X,a)[now].mask&VAL(C,X)=0
④now=now-1;
⑤ IFnow<0
⑥dom(x)←dom(x){a};
⑦ AddatoDEL(C,X);
⑧ IFdom(x)=∅
⑨ return false;
⑩ ENDIF
Functionsave(key,newdata,store)
① IF(key,olddata)∉top(store) for any
olddata
② Addnewdatatotop(store);
③ ENDIF
STRO算法是在回溯搜索过程中维持GAC的,所以需要在初始化时就使得约束表中的元组满足GAC.在初始化阶段,VAL(C,X)中每个位值都设置为1,LAST(C,X,a)等于最后一个位支持的位置,DEL(C,X)初始为空.
STRO算法首先经过第1步短表压缩后,开始动态删除无效的元组(调用deleteInvalidTuple方法),遍历DEL中所有的变量,将变量的所有支持删除,并清空DEL(C,X)数据结构,同时记录VAL(C,X)的值.在STRO算法中support和support*的值只在创建时计算,不会有更改,动态变化的是VAL(C,X)的值,用于记录当前约束表中元组的有效性.由于在DEL(C,X)中存储的是确定的已被删除的值,所以在删除无效元组阶段验证短支持有效性时,我们严格要求提τi[x]=a,即用support*辅助删除无效元组.
在搜索支持阶段(调用searchSupport方法),STRO将为约束范围内的每一个变量的每一个变量值进行位支持的有效性检查.若support(C,X,a)[now].mask&VAL(C,X)=0,则表明在位支持中没有包含有效元祖.now是当前操作的位支持,当now<0表明变量值没有有效的位支持,将该变量值删除并加入到DEL数据结构中.算法中函数save中保存的数据将用于算法回溯时恢复现场使用.其中restoreV中保存的是VAL(C,X)的值,restoreL中记录的是LAST(C,X,a)数据结构的值.STRO算法在搜索支持后,由于为当前约束表中的每个变量值都维持了至少一个支持,所以约束是满足GAC的.
Jefferson等人[9]已详细分析了STR2与Short-STR2算法的复杂度:对于一个值域大小为d且有t个元祖的变量集合U,STR2算法的复杂度为O(|U|d+|Sval|+|U|t),ShortSTR2算法的复杂度为O(rd+|Sval|+|U|t).其中Sval是STR2及ShortSTR2算法中用于保存相对于前一次的调用,论域发生改变的未赋值的变量,r为ShortSTR2算法中变量在主循环的时间消耗.
定理1. 对于r元约束,d为变量的最大值域,sn为表中各个变量值的位短支持总数,在一条长度为m的搜索路径上,STRO算法的最坏时间复杂度为O(sn+r2d2+m).
证明. STRO算法维持GAC虽然有3个阶段的操作,但主要的时间消耗在删除无效元组和寻找支持2个阶段.其中在删除无效元组时,若DEL(C,X)≠∅,则DEL(C,X)中变量的每个变量值都要被处理一次,所以最坏时间复杂度为O(sn).寻找支持阶段,LAST(C,X,a)值不变时,时间复杂度为O(r2d2);LAST(C,X,a)值改变时,遍历了所有的位支持,所以STRO算法总的最坏时间复杂度为O(sn+r2d2+m).
证毕.
3 实验结果与分析
为了展示新表压缩算法STRO的优化效果,本文实验对比了STRO,STR2,ShortSTR2,STRbit算法的性能.文中实验环境为Intel®CoreTMi7-3770 CPU@ 3.40 GHz,8.00 GB的RAM,Java语言,所有算法采用的变量启发式为dom/ddeg,变量值启发式为字典序[13],实验中的经典测试用例来自XCSP2数据库[14],其中MDD0.7和MDD0.9以及rand-5-2x实例来自STR2-C论文中提出的benchmark实例[15].
表5中的数据是3种算法对于每类benchmark实例进行测试,各个算法消耗的平均时间、运行时间单位为s,实例的最高运行时间设置为600 s,大于600 s则为timeout.实验测试了19个系列,共861组实例,表5中黑体为该系列3个算法中最短平均时间.实验结果表明,在90%以上的benchmark实例上,STRO算法的时间都是最优的.尤其在MDD0.9实例上,STRO算法的运行速度为STR2算法的20倍左右,是ShortSTR2算法的3倍左右;在MDD0.7实例中,STRO算法的运行速度也可达到STR2算法的10倍左右.这是由于在这2组实例上,STRO算法的压缩率非常大,所以提升效果特别明显.而由于rand-8,tsp和aim-50系列实例的约束表在回溯搜索中的平均大小特别小(<0.004),而STRO算法相较于STR2算法需要有压缩表的过程,所以STR2算法消耗时间要比STRO算法更少一些.在jnh实例中,由于短支持位表较小,所以STRO算法与ShortSTR2算法的CPU时间接近.
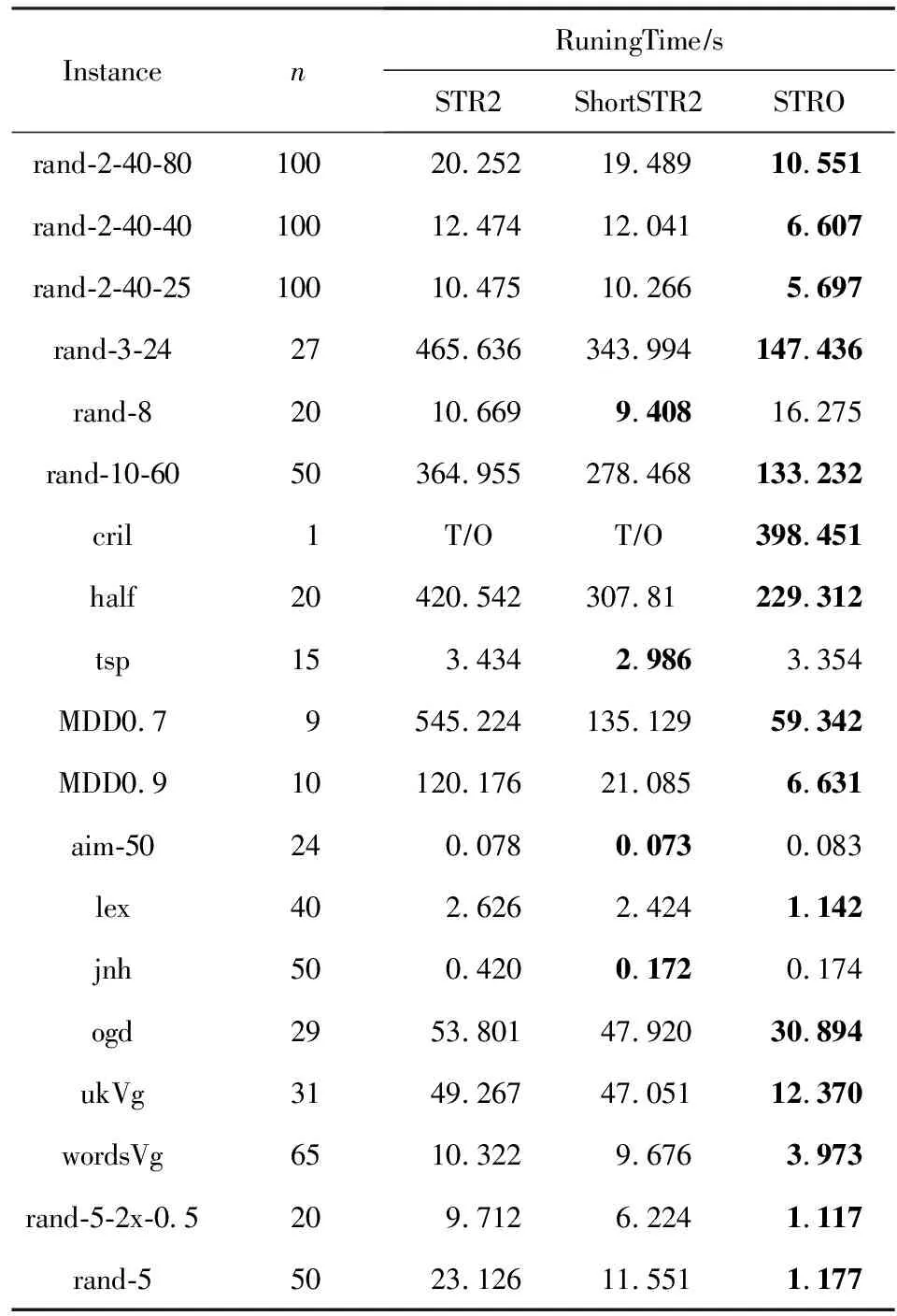
Table 5 Running Time of STR2,ShortSTR2 and STRO表5 STR2,ShortSTR2,STRO运行时间比较
Note: The minimum average time of each row is in bold.
图1中的矩形代表的是用STR2及STRO算法分别测试benchmark实例中经常出现的时间结点区间.在图1中可以清楚看到STRO算法中绝大部分的时间是集中在10 s以下,STRO算法整体运行时间大多都小于STR2算法.
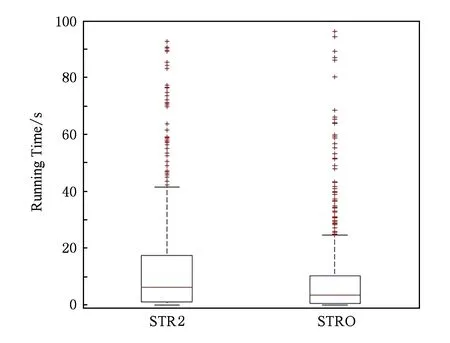
Fig. 1 Comparison of running time between STR2 and STRO图1 STR2 与STRO时间对比盒图
在图2中用散点图的方式更加清晰地比较STRO与STR2,ShortSTR2算法的时间性能.图2中每个点都代表一个具体的实例,图2中斜线代表2个对比算法在测试实例上消耗时间相同.在图2(a)和图2(b)中大部分的点都集中在右下角,所以STRO算法相对于ShortSTR2和STR2算法,都耗时更少、性能更好.对比图2(a)和图2(b)发现:图2(b)中的结点更远离红线,因此,STRO算法相对于STR2算法的速度提升效果比STRO算法相对于ShortSTR2算法要更为明显.并且ShortSTR2算法和STR2算法运行超时(>600 s)时,STRO算法都能够在600 s内完成实例的测试.
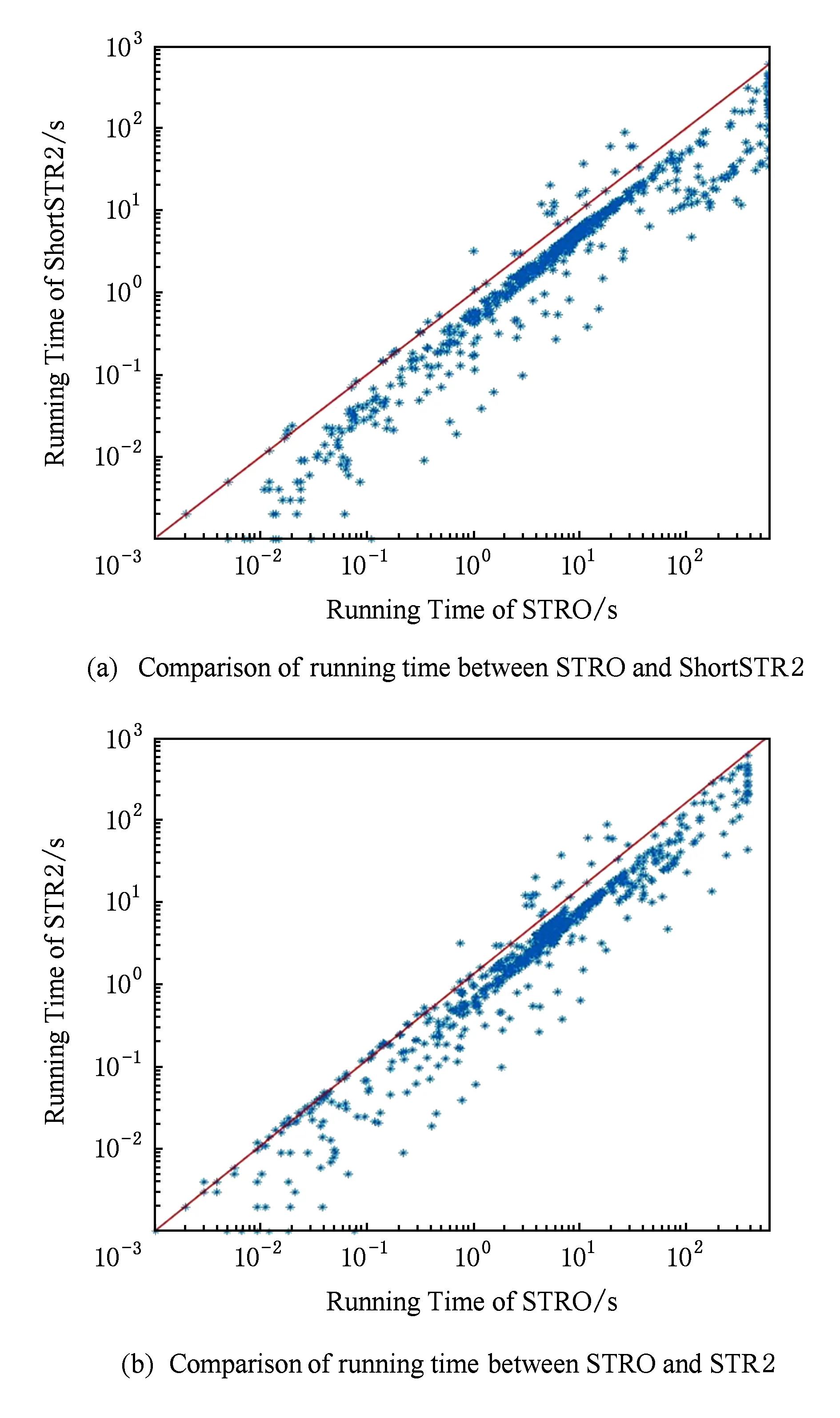
Fig. 2 Running time of STRO, STR2 and ShortSTR2图2 STRO与STR2及ShortSTR2时间性能对比
STRO和STRbit算法的性能对比结果展示在表6中,在表6中将压缩率和每秒处理的结点数作为衡量算法性能的参数.可以看到,STRO与STRbit算法相比,STRO算法整体的压缩率都比STRbit算法压缩率要大,尤其对于实例MDD0.7,STRO算法压缩率是STRbit算法的4倍左右,每秒处理的结点数是2倍以上.对于MDD0.9实例,STRO算法压缩率是STRbit算法的20倍以上,每秒处理的结点数也达到了10倍以上.在实验中,在少数实例上STRO算法速度提升效果并不大,这是由于STRO算法需要将原约束表转化为短表,维持了额外的数据结构,有额外的时间开销,但总体来讲在时间上可以替代STRbit算法.
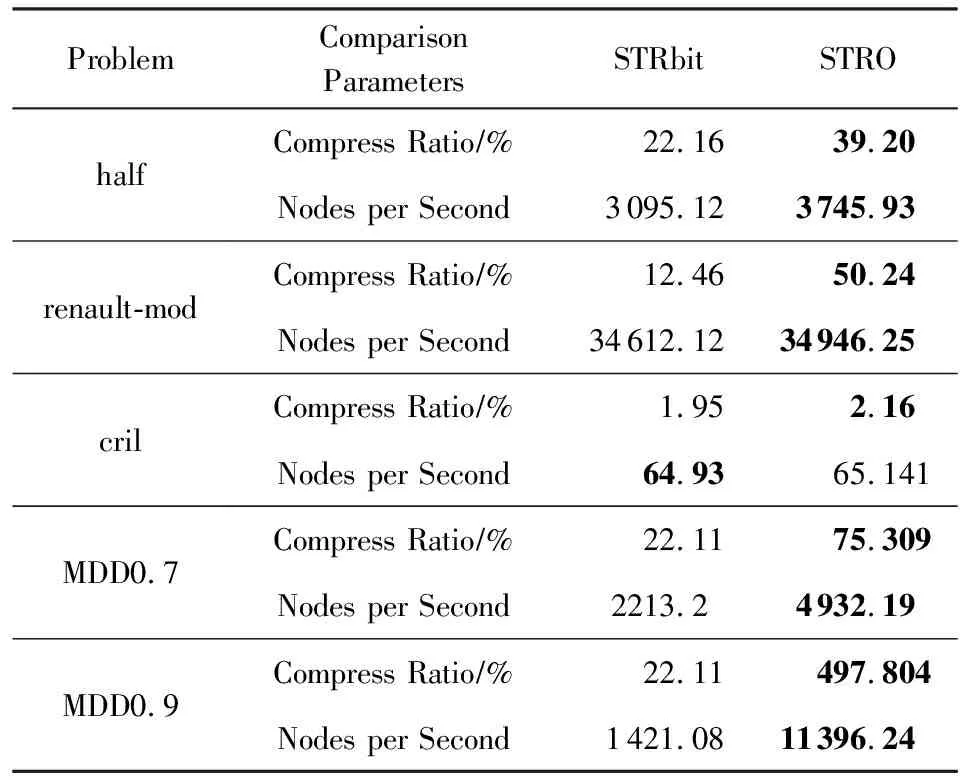
Table 6 Performance Comparison Between STRbit and STRO表6 STRbit与STRO算法的性能对比
Note: The minimum average time of each row is in bold.
4 总 结
表缩减算法STR在表约束上求解效率非常高,对于STR算法的改进算法,近些年来也相继被提出.其中通过表压缩的方式,将约束表的空间压缩从而提高效率,是STR算法的一种优化方式.而其中的ShortSTR2算法,在压缩率较低的情况下对于STR2算法的优化效果并不明显.这是由于目前没有直接的短表,需要短支持方法维护额外的数据结构,将原有的约束表转化为短表,所以消耗了一部分时间.但是相比STR算法,ShortSTR2算法节约了空间,可以传播更多的结点.基于此本文将短支持方法辅以位操作,保留短支持方法的优势,并结合位操作提出STRO算法.实验结果表明:除了在约束表规模特别小的情况下,效果与STR2算法及ShortSTR2算法差别不大,STRO算法在大多数情况下优于STR2算法及ShortSTR2算法;与STRbit算法相比,在CPU处理时间上可以替代STRbit算法,但是表压缩率更大,更加节省空间.

