泛Kriging法在海上短波通信频率预测中的应用
(海军大连舰艇学院 信息系统系,辽宁 大连116018)
1 引 言
短波通信在舰岸通信、舰空通信、舰艇编队通信等方面具有重要意义。2017年9月,在美国空军授意下,柯林斯公司成功演示了8 000 km新短波通信系统,旨在支持卫星通信盲区的作战通信。现代技术的进步推动着短波通信快速建链[1]、大容量数据传输的发展,但频率预测及选择问题一直制约着短波远程通信质量的提升。由短波信道模型发展建立的中长期预报软件实现了复杂链路的程序化[2],但输入参数条件苛刻,适用范围受限,严重影响其在海上通信中的应用效果。基于模糊小波、神经网络、混沌理论等现代算法的预测方法虽提升了预测精度,但工程实现的难度较大[3]。因此,频率预测仍是短波通信中急需解决的关键问题。目前,已有研究人员将普通克里格法(Ordinary Kriging Algorithm)应用于短波通信可用频率插值中,但该方法的应用前提是电离层处于平稳状态[4]。考虑到电离层变化的连续性及等离子体、不均匀体的漂移特性[5-6]。本文将泛克里格法(Universal Kriging Algorithm)引入海上短波通信频率预测中。泛克里格方法基于数据的变化趋势,给出变化方向上的漂移方程,利用样本数据反映的空间结构信息,可在空间相关变程内对区域化变量进行无偏最优估计。本文利用舰艇海上活动中的通信频率数据,对基于泛克里格法的海上短波通信频率预测方法的可行性进行验证,研究通信频率沿水平方向的变化特性和变异函数理论模型的应用选择,给出具体的方法步骤和预测过程。
2 泛克里格法和变异函数
克里格法属于地质统计学范畴,起初被应用于地质矿石的研究中,随研究目的和研究条件的变化派生出多种形式,逐步应用于地质污染、降水分析、气温预报等多方面的研究[7-9]。由于电离层沿水平方向存在漂移,且区域化变量在实际应用中很难满足二阶平稳假设,因此选用适于通信环境的线性泛克里格方法对频率的变化特征进行描述。
2.1 泛克里格法
假设空间位置x上的区域化变量Z(x)在研究范围内是非平稳的,即Z(x)的数学期望是一个函数,表示为E[Z(x)]=f(x)。该函数被定义为Z(x)的漂移函数,描述了区域化变量随主导因素的变化情况,通常采用多项式的表达形式:
式中:fi(x)是与空间位置相关的已知函数,ai为未知参数。取n个空间点xi(i=1,2,…,n),可得对应的Z(xi),应用线性泛克里格法对样本区域内任意一点上的区域化变量进行估计,重构结果Z*(x)如式(1)所示:
(1)
在无偏最优估计条件下求解系数λi(i=1,2,…,n),代入式(1),可得估计值Z*(x)。
2.2 理论变异函数
变异函数γ(h)描述了样本数据的空间结构特征,记作点x和x+h处区域化变量Z(x)和Z(x+h)差的方差的一半,具体表达式为
(2)
式中:滞后距h为向量。
由于样本数据有限,通常在定量的描述区域特征时,需根据实测数据下离散的实验变异函数值构建理论变异函数模型即滞后距h与变异函数γ(h)的关系模型,表达区域变量的空间相关性。具体的求解步骤如下:
Step1 计算样本点间的滞后距h:
(3)
式中:Long(A)、Lat(A)分别表示估值点A处的经度和纬度;φ是电离层距离转化比例系数,一般取0.8~4[4]。
Step2 计算实验变异函数γ*(h),如公式(4)所示:
(4)
式中:N是样本点间滞后距为h的点对数。
Step3 利用最小二乘法、加权回归法或遗传算法等方法对实验变异函数进行拟合,获得变异函数γ(h)与滞后距h的关系曲线。
3 泛克里格法在海上短波通信频率预测中的应用
3.1 数据来源及方法应用
在舰船参与海上活动的过程中,频率管理系统保存了大量实用短波通信频率数据。为避免电离层结构受昼夜更替、季节变化等因素的影响,综合数据量的要求,提高预测精度,选取太阳活动低年的夏季上午9~11时,舰船与同一地面固定台站间的通信频率,对理论变异函数模型进行构建。该频率通过了链路质量分析筛选,接收端的信号强度较好,传输时延较低,具有良好的通信质量和传输效果。通过随机选取的实测最高可用频率,验证基于泛克里格法的海上短波通信频率预测方法的有效性。预测方法应用的具体流程如图1所示。
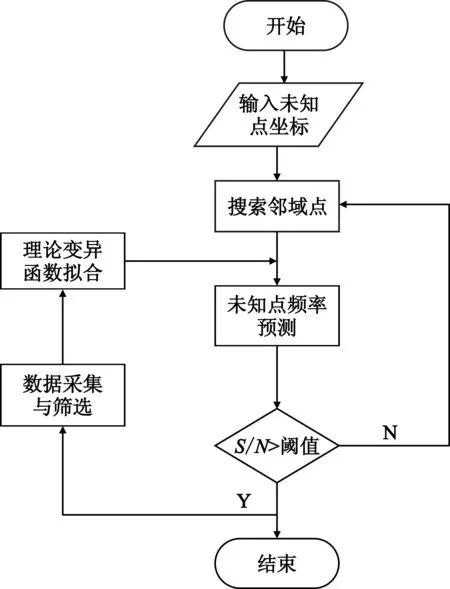
图1 短波通信频率预测流程图Fig.1 Flow chart of shortwave communication frequency prediction
对应的步骤如下:
Step1 输入未知点坐标信息,在空间相关变程内搜索与预测时间点相近的邻域点,作为参与频率预测的待用点。
Step2 基于大量实测数据由2.2节的算法步骤构建理论变异函数模型。依式(3)计算未知点与邻域点和邻域点间的滞后距,并计算各滞后距对应的理论变异函数值,应用泛克里格法对未知点的通信频率进行重构。
Step3 验证预测频率的有效性和可靠性,若通信质量较好,输出结果并记录于数据库中,更新理论变异函数模型;若通信质量较差,重新搜索邻域点直至输出良好的通信频率。
3.2 变异函数拟合
由式(3)和式(4)计算实验数据下的(h,γ*(h))值,距离间隔设为2 km。选用有基台值的理论模型即球状模型、指数模型和高斯模型,应用最小二乘法,对离散数据(h,γ*(h))进行曲线拟合。块金值、基台值和变程是描述变异函数曲线的重要指标,分别描述了区域化变量的随机性、变化幅度和空间相关尺度。各模型的线性表达及块金值、变程、基台值的求解方法均记录在表1中。

表1 基于最小二乘法的理论模型表达及参数求解Tab.1 Expression of theoretical models and parameter solving based on least squares
(1)球状模型
球状模型的表达式为
(2)指数模型
指数模型的表达式为
(3)高斯模型
高斯模型的表达式为
各模型拟合曲线如图2所示,可观察到随着滞后距的增加,变异函数呈现单调递增趋势。这一现象表明,在与地面固定台站建立短波通信的过程中,当海上移动台站间的距离变远时,短波通信频率的相关性变弱;当海上移动台站间的距离变近时,短波通信频率的相关性变强。表2详细列出了各模型下参数计算值。

(a)球状模型拟合

(b)指数模型拟合
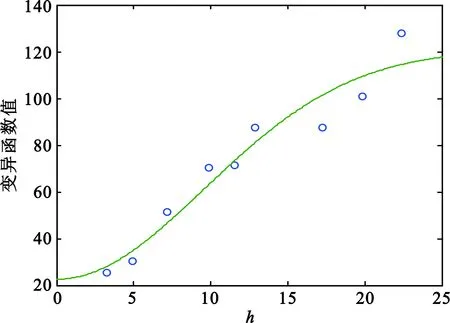
(c)高斯模型拟合图2 各模型拟合曲线Fig.2 Fitting curve of each model

表2 各模型对应参数Tab.2 Corresponding parameters of each model
3.3 泛克里格预测及精度对比
随机选取5个移动通信位置点(记作A点~E点),其相对位置如图3所示。记录各点与同一固定台站进行短波通信时的最高可用频率,作为区域化变量Z(x),如表3所示。假设任意一点为未知点,基于泛克里格方法,利用已知邻域点的通信频率数据,估计未知点的短波通信最高可用频率并计算出相对误差。下面以A点为例,对其最高可用频率进行估计,并依照此方法对其余各点进行交叉验证。

图3 A~E点相对位置图Fig.3 Relative position of point A~E

表3 各点实测短波最高可用频率Tab.3 The highest available frequency of measured shortwave at each point
由公式(3)计算已知的邻域点与未知点及邻域点之间的滞后距,并依次代入各变异函数模型,得到对应的理论变异函数值,其中电离层距离转化比例系数取φ=2。表4是球状模型下以A点为未知点的(h,γ(h))值。

表4 上三角是滞后距下三角是理论变异函数值Tab.4 The upper triangle is h and the lower triangle is γ(h)
泛克里格矩阵可写为
在教学中,要充分使用“班班通”多媒体。由于在课堂上要留足学生的自学时间,教师掌握的时间就相对减少要在有限的时间内启迪学生思维,开发学生创造力,就要充分利用多媒体教学手段让学生学得轻松愉快,可以使学生积极主动参与,还可以使学生思维活跃。在“启”中合理运用电教手段,可以创设情景激发学生的激情;在“读练”中巧用,能扫除阅读障碍有助于理解词义、句意;在“知”中运用电教手段,能强化教材重点,突破难点;在“结”中运用电教手段,可以巩固、加深对教材内容的了解。
Z*(x0)=ZA-1B。
(5)
式中:
(6)
(7)
(8)
n为邻域点个数。
由于电离层等离子体在水平方向上存在漂移,且不均匀体的漂移速度沿传播方向线性增加[5-6],因此,采用沿纬度方向的线性漂移形式,其表达式为f(x)=a0+a1x,x表示纬度。将n=4代入式(6)~(8),同时代入理论变异函数值及B点~E点经、纬度,求得A点处的短波最高可用通信频率预测值Z*(x0)为
Z*(x0)=Z(A-1B)=9.750 5。
重构得到的频率值与实际频率值间的相对误差σ*(%)为
(9)
代入A点实测值和预测值,求得A点重构的相对误差σ*(%)=4.406 9。
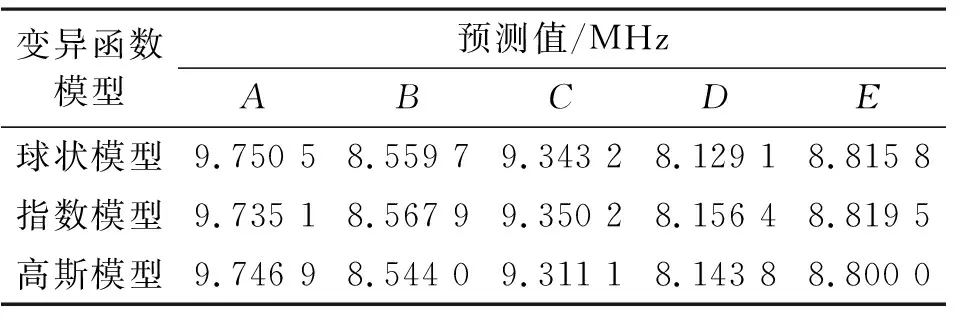
表5 各变异函数模型下的泛克里格预测值Tab.5 Predicted values for each variation function model by Universal Kriging

表6 基于泛克里格法的各变异函数模型下的相对误差及相对误差均值Tab.6 Relative error and average relative error of each variogram model based on Universal Kriging
在REC533模型参数设置如表7所示,其余参数设置依照系统设置的缺省值[10]的条件下,比较基于普通克里格法和REC533模型的海上短波通信频率预测方法的可靠性,结果如表8和表9所示。
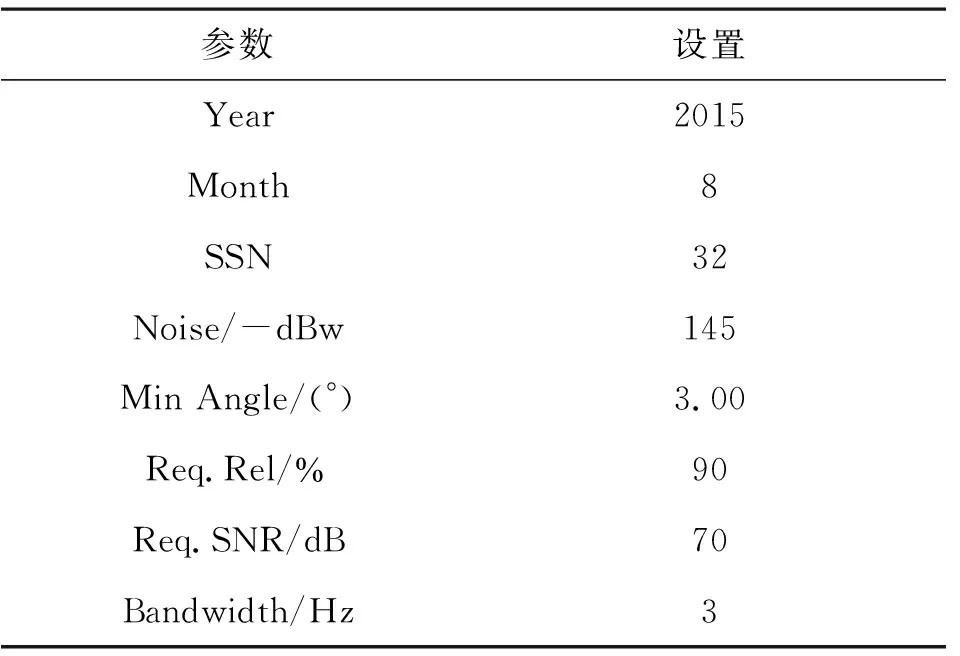
表7 REC533模型参数设置Tab.7 REC533 model parameter settings

表8 基于普通克里格法的各变异函数模型下的相对误差及相对误差均值Tab.8 Relative error and average relative error of each variogram model based on Ordinary Kriging

表9 REC533模型预测结果Tab.9 Predicted result by REC533 model
3.4 实验结果分析
通过以上数据分析,结合实际应用情况,可得出如下结论:
利用太阳活动低年期间某海域舰船活动的通信数据,构建了多种变异函数模型,实现了基于线性泛克里格法的通信频率预测。实验结果表明,在通信频率沿纬度方向存在线性漂移时,各模型预测结果的相对误差均值均低于2.5%。高斯模型下B点预测值与实测值的相对误差低至0.517 6%,具有良好的预测精度。在实际应用中,通信部门为避免信息传输过程中多次换频,通常取最高可用频率的85%作为最佳工作频率。因此,泛克里格法适用于海上短波通信频率的预测。在空间相关变程内,利用泛克里格法进行频率预测,能够为未知海域短波通信提供保障,具有工程应用价值。
(2)邻域点均匀分布时短波通信频率预测结果更准确
由表6可以观察到,变异函数模型相同时,随未知点位置变化,估计误差值存在明显差异。结合图3中各点位置信息,综合大量数据分析可知,该算法的预测精度与邻域点的分布有关。观察图3可知A、C、D、E点较均匀地分布在B点周围,使B点能够克服各向异性,得到较高精度的预测值。而当未知点位置相对较偏时,各向异性显著,其预测结果偏离实测值。因此,在进行泛克里格法频率预测时,均匀地选取邻域点可以有效提高预测精度。
(3)基于泛克里格法的海上短波通信频率预测结果的可靠性较高
比较基于普通克里格法和REC533模型可以看出,基于泛克里格法的海上短波通信频率预测结果更贴近真实值,预测效果更好。普通克里格法不考虑电离层等离子体、不均匀体的漂移特性,导致各模型预测结果差异较大,受邻域点方向的变异特性影响严重。REC533模型建立时中国区域电离层结构信息较少有关,导致预测精度受限。在应用泛克里格法预测时,各模型预测精度由高至低为高斯模型>球状模型>指数模型,但差异较小,均具有较高的估计精度,在实际应用中可依据通信设备选择合适的预测模型。
4 结束语
本文结合电离层漂移特性,确定了沿纬度方向的漂移形式,验证了泛克里格法在海上短波通信频率预测中具有良好的应用性,且估计精度较高,可用于保障海上通信。此方法充分利用历史数据的空间相关性,弥补了以往在时间维度上进行频率预测的不足,同时还避免了探测选频过程耗时长、占用信道、目标易暴露等弊端,对未知海域的短波频率预测工作具有重要意义。在实际应用中,需尽可能地使邻域点均匀分布在未知点周围,以提高预测精度。因此,可进一步研究适合海上通信的邻域选点技术,完善基于泛克里格法的海上短波通信频率预测方法。

