离散非线性系统的事件驱动最优控制

张 欣, 薄迎春

(中国石油大学 信息与控制工程学院, 山东 青岛 266580)

0 引 言

因为在降低数据传输次数和计算量的同时还能保证具有较好的控制性能,因此,事件驱动控制近年来一直是控制领域的研究热点。与传统的采样方法不同,事件驱动提供了一个只在状态采样点更新的非周期策略。只有当事件触发条件不被满足时,对系统状态进行采样, 更新系统的控制率。在2次更新之间采用零阶保持器保证控制器的输出。

目前,已有许多文献利用事件驱动控制方案解决不同的控制问题[1-5]。文献[3]研究了线性系统的周期事件驱动控制。文献[4]将事件驱动控制扩展到了离散非线性系统中。Tallaprogada等在文献[5]中给出了事件驱动方法在非线性跟踪问题上的控制方案。为了在事件驱动控制机制下研究系统的最优控制问题, 近期很多学者开始将自适应动态规划(adaptive dynamic programming, ADP)方法引入到事件驱动控制方案中。ADP作为解决非线性系统最优控制问题的有效方法得到了广泛关注[6-9]。文献[10]求解了连续非线性系统的事件驱动自适应最优控制。S.Jagannathan等[11]研究了不确定连续非线性系统的事件驱动控制方法。王鼎等在文献[12]中针对连续系统的H∞控制问题, 提出了基于混合数据和事件驱动的控制方案。文献[13]研究了离散非线性系统的自适应事件驱动控制方法。

为了降低数据传输次数、计算量和神经网络权值的训练量,针对离散非线性系统的最优控制问题, 提出了一种基于单网络值迭代算法的事件驱动控制方案。充分发挥了ADP算法、事件驱动控制和神经网络各自的优势。与典型的ADP算法相比, 舍弃了用3个神经网络分别构建模型网、控制网和评价网的架构。只利用一个神经网络来构建评价网, 继而省略了模型网和控制网的神经网络权值训练量。并且引入事件驱动控制机制来有效地降低控制策略的计算次数以及系统状态和控制器之间的数据传输。

1 离散非线性系统的最优控制

考虑如下的离散非线性系统:

xk+1=f(xk)+g(xk)u(xk)

(1)

相应的性能指标函数为普通二次型形式:

(2)

将性能指标函数(2)展开, 可得

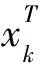
(3)

根据Bellman最优性原理[14],最优值函数V*(xk)是时变的, 并且满足离散HJB方程:

(4)

最优控制策略u*(xk)应该保证HJB方程一阶导数为零, 可求得

2 事件驱动最优控制

2.1 事件驱动机制

‖ek‖≤eT,k∈[ki,ki+1)

其中:ek=xki-xk为事件驱动误差;eT为事件驱动阈值。仅当‖ek‖>eT时, 触发条件不被满足,事件驱动状态误差被重置为零,同时更新控制策略μ(xki)≜u(xki),并且通过零阶保持器保证在k∈[ki,ki+1]时间段内系统的控制策略不变,直到下一次事件触发。因此, 系统状态方程(1)重写为

xk+1=f(xk)+g(xk)μ(ek+xk),k∈[ki,ki+1)

(5)

最优状态反馈控制策略应该表示为

(6)

假设1 存在正数L, 满足[13]

‖xk+1‖≤L‖ek‖+L‖xk‖

由于ek+1=xki-xk+1,k∈[ki,ki+1),根据假设1,可得

因此,定义事件驱动阈值为

其中常数α∈(0,1]为事件驱动阈值适应率,主要用来调节采样频率。

定理1 对于离散非线性系统(5),相应的性能指标函数为(2),当采用公式(6)中的事件驱动最优控制策略时,则闭环系统(5)是渐近稳定的。

证明 选取Lyapunov函数为

该Lyapunov函数的一阶差分方程为ΔV=V(xk+1)-V(xk)。

情况1 事件没有触发,∀k∈[ki,ki+1)

对于任意xk≠0,有ΔV<0,即Lyapunov函数的一阶差分方程是负定的。

情况2 事件被触发,∀k=ki+1

对于任意xki+1≠0,有ΔV<0。综合情况1和情况2可得,Lyapunov函数的一阶差分方程是负定的,根据Lyapunov理论可得,闭环系统(5)是渐近稳定的。证明完毕。

2.2 单网络值迭代算法

事件驱动机制将整个控制过程分为了若干部分,控制输入仅在采样时刻更新,其他时刻保持不变,因此当k∈[ki,ki+1)时,控制策略为

其中V*(x)需要通过求解离散HJB方程(4)来获得。而对于离散非线性系统来说,HJB方程(4)的解析解很难直接求解。因此本文将采用单网络值迭代的ADP算法来求解HJB方程,进而获得事件驱动近似最优控制策略。

单网络值迭代算法仅利用一个神经网络来构建评价网,省略了典型ADP算法中的执行网。如果系统动态已知,那么模型网也可以省略。典型ADP算法中执行网的输出可以直接通过公式(6)计算获得,系统状态可以通过方程(5)计算得出。

采用一个三层神经网络来构建评价网

(7)

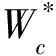
典型ADP值迭代算法是通过在序列Vj(xk)和序列uj(xk)之间反复迭代获得最优值函数和最优控制策略。在单网络值迭代算法中,序列Vj(xk)为评价网输出

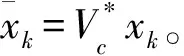
其中:j代表迭代次数;k表示时间步,xk表示k时刻系统的状态;uj(xk)表示k时刻第j次迭代的控制策略;Vj(xk)表示k时刻第j次迭代的值函数。当迭代次数j→∞时,序列Vj(xk)收敛到离散HJB方程(4)的解,即V∞(xk)=V*(xk),序列uj(xk)收敛到最优的控制策略,即u∞(xk)=u*(xk)[15]。

定义评价网的训练误差为

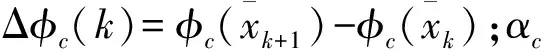
其中Δεc(k)=εc(k+1)-εck。

接下来,证明评价网权值估计误差的收敛性。在证明开始之前,给出下列假设条件。

假设2 1) 评价网激活函数有界,φcm≤‖φc(·)‖≤φcM;

2) Δεc(k)具有上界,满足‖Δεc(k)‖≤εcM。

定理2 评价网的权值更新规则为式(8)和式(9),如果下列不等式满足

证明 选取Lyapunov函数为

根据柯西不等式和公式(10),Lyapunov函数的一阶差分为

(13)

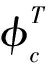
基于上述事件驱动机制和单网络值迭代算法,可以获得离散非线性系统的近似最优控制策略为

(14)

该单网络值迭代事件驱动控制方案具体的执行步骤如下:

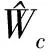
步骤2 令j=0,V0(xk)=0,计算u0(xk);

步骤3j=j+1;

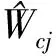
步骤5 如果‖Vj+1(xk)-Vj(xk)‖<ξ或者j>jmax,跳转步骤6,否则跳转步骤3;

步骤6 令i=0,k=0;

步骤7 计算事件触发误差ek和阈值eT;

步骤8 判断‖ek‖是否大于eT, 如果大于执行步骤9, 如果小于等于跳转步骤10;

步骤9 令i=i+1,xki=xk,ek=0,由公式(14)计算事件驱动最优控制策略u*(k);

步骤10 由公式(5)计算系统状态xk+1;

步骤11 如果‖xk+1‖≤或者i>imax,跳转步骤12,否则跳转步骤7;

步骤12 算法结束。

3 仿真验证

评价网训练了1 500次,前500次中加入了持续激励。图2为事件驱动误差的范数‖ek‖和阈值eT轨迹。图3展示了本文所提事件驱动ADP算法(ET-ADP)与典型ADP算法系统状态的对比情况。图4为近似最优控制输入轨迹。

仿真结果表明,本文所提的ET-ADP算法需要经过619步达到ò=10-5的稳态精度,但事件触发次数仅为81次,与传统的ADP算法相比,大大地降低了数据传输、控制输入的计算和神经网络的训练量,同时保持了良好的控制效果。

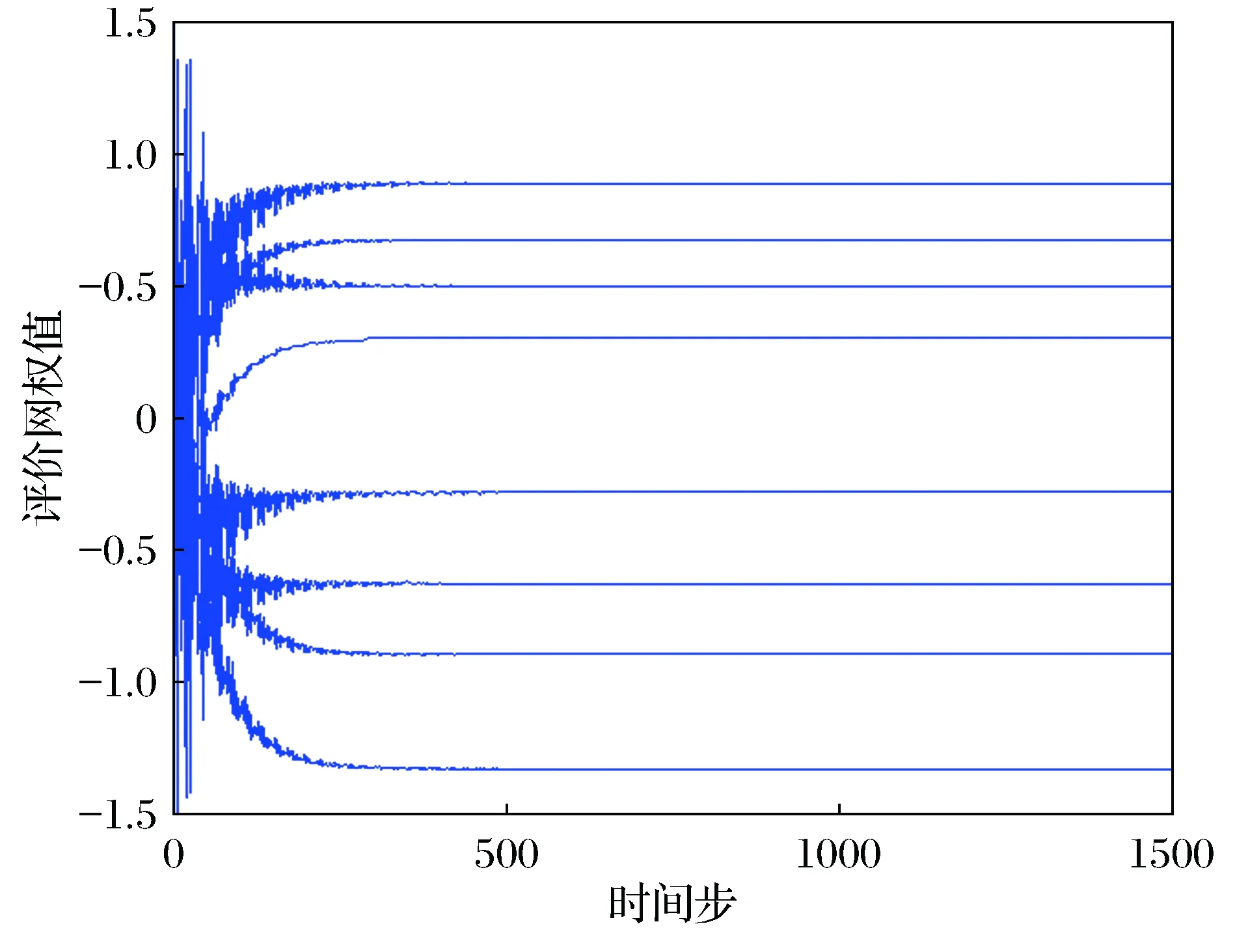
图1 评价网络权值收敛轨迹

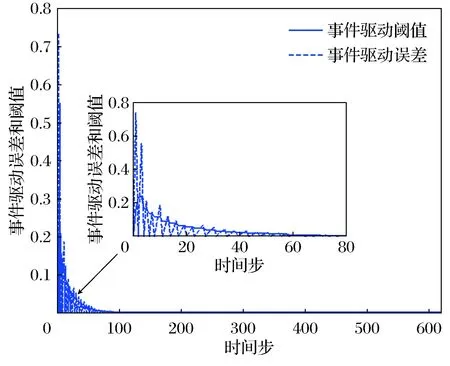
图2 事件驱动误差和阈值轨迹Fig.2 Trajectories of the ET error and threshold

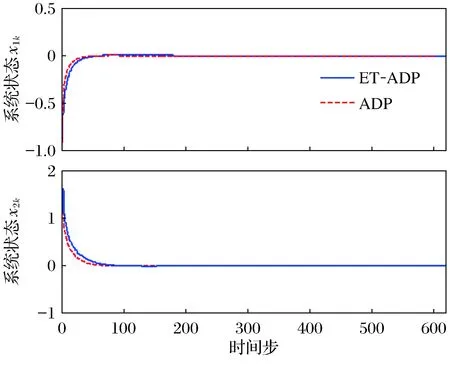
图3 系统状态轨迹Fig.3 Trajectories of the system states

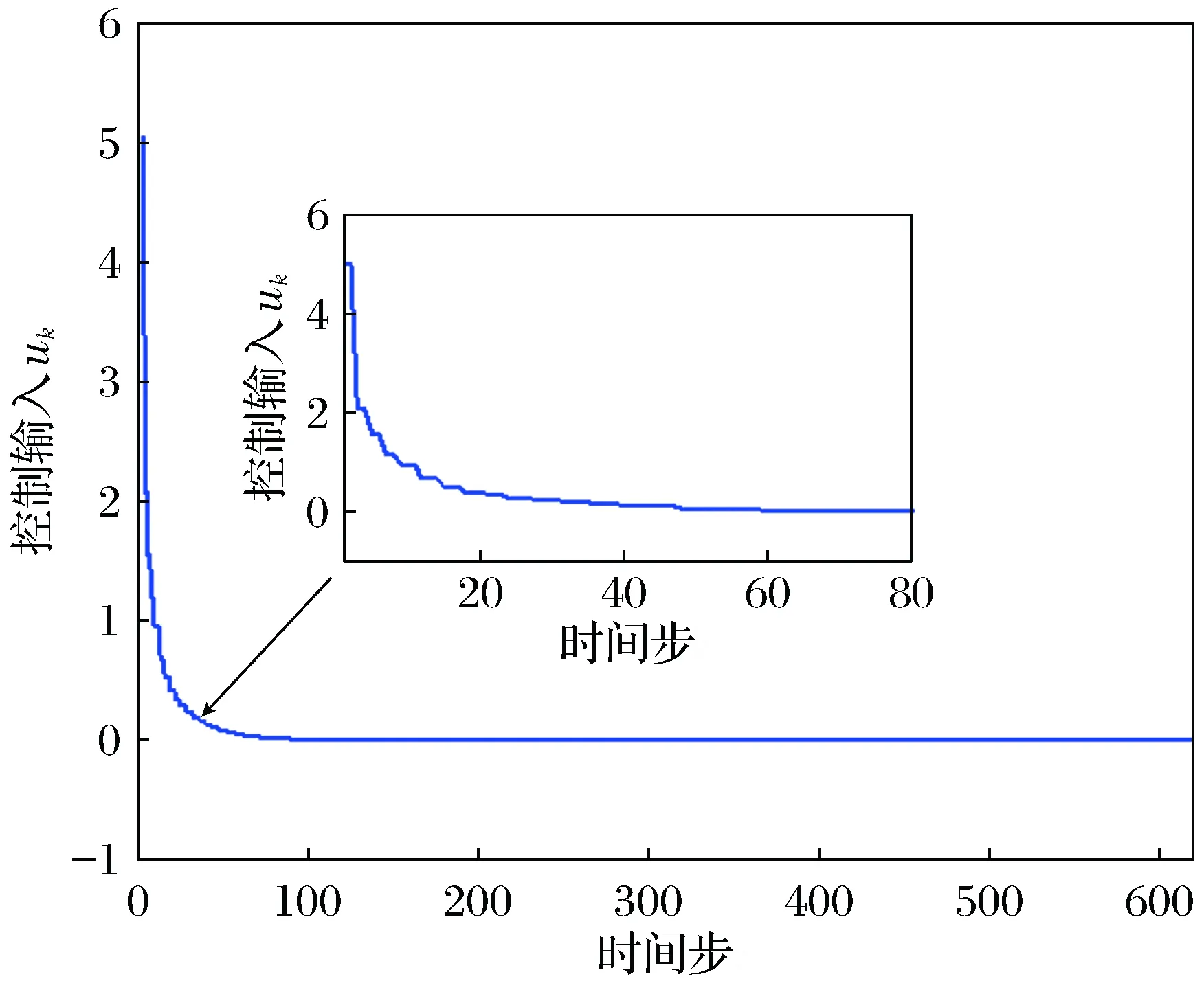
图4 控制输入轨迹Fig.4 Trajectories of the control input

4 结 论

本文研究了离散非线性系统的近似最优控制问题。结合ADP算法、事件驱动控制和神经网络思想,提出了一种基于单网络值迭代算法的事件驱动控制方案。首先,定义了新型的事件驱动阈值;然后,采用单网络值迭代算法,仅利用一个神经网络来构建评价网,利用Lyapunov理论证明了闭环系统的稳定性和评价网权值的收敛性;最后,将该方法应用到非线性系统的控制仿真实验中。结果表明所提方法有效,并成功地降低了数据传输次数、计算量以及神经网络权值的训练量。