基于临近听域超声波TDOA室内定位的实现

齐 恒 彭林宁 姜 禹 胡爱群

(东南大学网络空间安全学院，南京，211189)

引 言

定位技术已被广泛应用于生活中，其中应用最为广泛的是GPS定位。但是GPS信号无法在室内接收，不适合用作室内场景中定位的技术。因此，室内定位技术成为了研究的热点。现阶段有许多适合室内定位的方案，例如基于WIFI、可见光和蓝牙的定位技术[1-5]，这些技术大部分依据接收信号的强度或推算接收信号的到达角度，从而进一步实现室内位置的估算，其定位的准确性较低。此外，有研究使用超宽带(Ultra-wideband，UWB)等无线信号进行基于信号到达时间(Time of arrival，TOA)和到达角度(Angle of arrival,AOA)的室内定位[6]。也有文献提出了使用接收信号强度比较(Receive signal strength compare，RSSC)来定位[7]。然而，由于无线电信号的传播速度非常快，实现基于无线信号TOA的室内定位方案需要较高的成本。基于无线信号AOA的定位方案受不同天线及接收通道射频器件偏差的影响较大，其实际定位的精度并不高。

超声波定位也是可以采用的室内定位的方案之一。Bat系统是较为著名的超声波室内定位系统之一[8]。Bat系统使用行时间(Time of flight，TOF)方法可以对空间内目标进行三维的定位。Bat系统通过一个超声波发射设备发射超声波，由安装在天花板上的接收机接收。几个接收机将数据传入计算机计算出发射设备位置。Cricket系统也是使用了基于到达时间差(Time difference of arrival，TDOA)的定位技术[9]。这一系统精度很高，可以达到1～2 cm。之后的一些定位方案在定位基础上对系统跟踪目标的能力做了一些优化。有文献提出了一种在二维平面上定位的方案[10]。其定位方法基于TDOA原理，通过卡尔曼滤波原理在追踪目标方面进行优化。另外，在三维空间中的定位方案[11]中，有研究采用了Taylor展开法以及卡尔曼滤波来实现定位。这些超声波定位方案的成本大多偏高，而且基本都需要定制硬件，不太适合使用普通的终端，如智能手机等自带音频麦克风的设备接收信号。因此，在实际应用推广上具有一定的难度。

基于以上超声波定位系统的缺点，设计了一种临近听域超声波的室内定位系统。该定位系统使用普通高音喇叭发射超声波信号，由手机的麦克风接收超声波信号并进行离线的位置估算。使用普通的高音喇叭发射大于20 kHz的超声波信号，将极大地降低基于超声波室内定位系统的实现成本。基于本论文提出的低成本定位实现构想，设计了具体的硬件实现方案。首先，在发射端，利用伪随机码的正交性来区分不同高音喇叭的超声波。在接收端，设计了基于FFT的频域搜索算法得到各路超声波信号的到达时间并计算时间差。最后应用一种修正的秩-1拟牛顿算法[12]得到目标位置的估计并和经典的CHAN算法进行了比较。仿真和实验结果表明，在有3个发射机的情况下，使用修正秩-1拟牛顿法所得目标位置估计精度与CHAN算法[13]基本相同。

1 基于超声波TDOA定位系统

1.1 TDOA定位模型

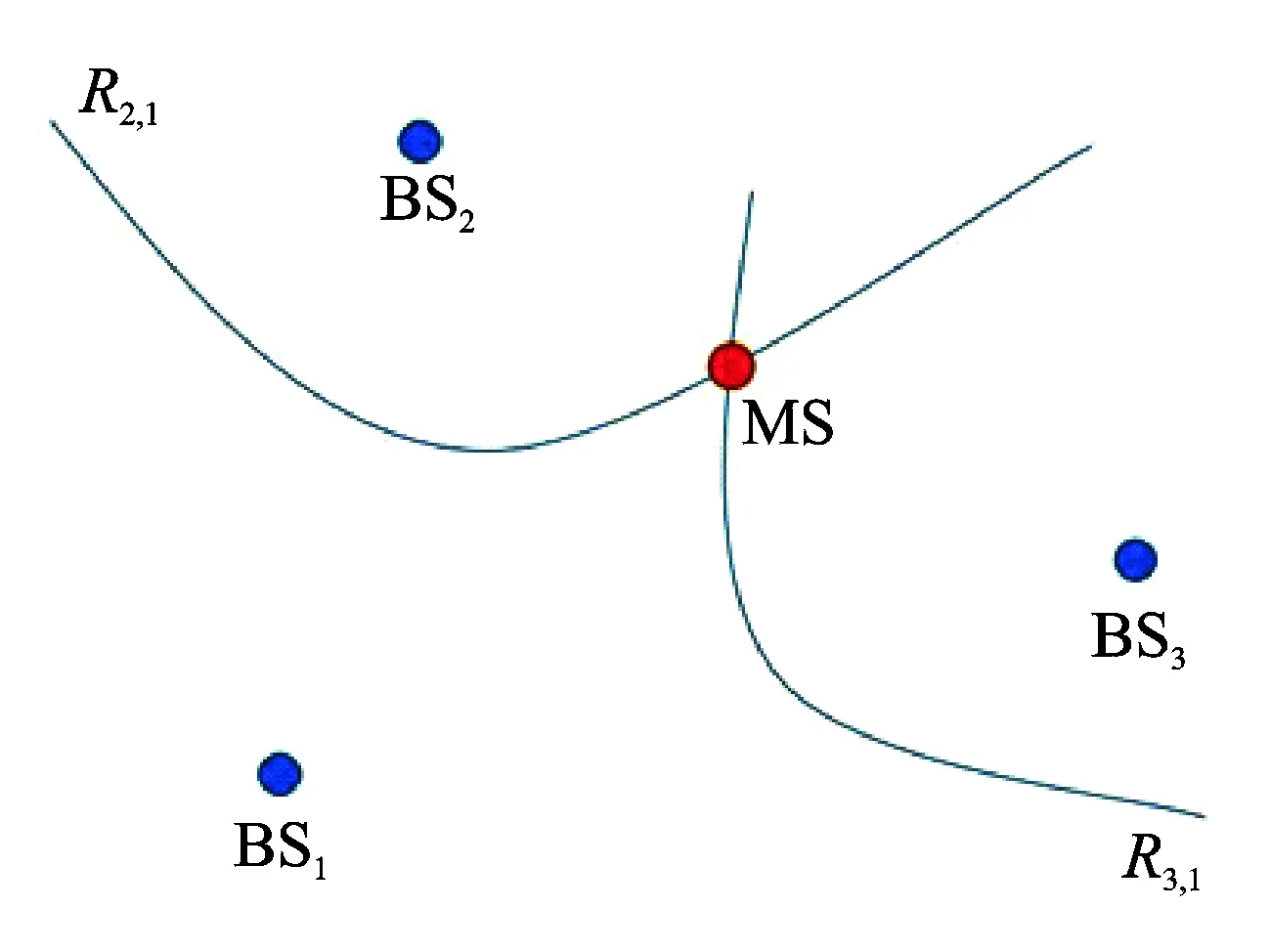
图1 基于TDOA的定位模型Fig.1 Model of positioning based on TDOA

如图1所示，将发射信号的发射机称作基站(Base station，BS)，而接收信号的设备称为移动站(Mobile station，MS)。保持BS同步， 使几个BS同时发出超声波信号。由几个信号到达MS的时间差可以计算出MS的位置。在实际系统中，可以使用码分多址技术来区分几个BS发射的信号。通过与BS发射信号的同步，即可得到不同信号的到达时间差，从而得到不同BS到MS的距离之差，即

Ri,1=vti,1=Ri-R1

(1)

式中ti,1是编号为i的BS发射信号到达时间与编号为1的BS所发射信号到达时间之差，且有

(2)

式中：(Xi,Yi)是编号为i的BS的坐标，(x,y)是MS的坐标。

1.2 基于TDOA的目标位置估计方法

在本系统中，将一种修正秩-1拟牛顿法应用于基于TDOA的目标位置估计中。文献[14]介绍了一种适用牛顿法的模型，这一模型同样适用实验。对于TDOA估计值的关系可以表示为

d=Gr+n

(3)

式中：d=[R2,1,R3,1,…,RM,1]T，G的第1列是全为-1的(M-1)×1的列向量，G中其余部分为(M-1)×(M-1)的单位矩阵，组成的整个矩阵为(M-1)×M矩阵，r=[R1,R2,…,RM]T，n=[n2,1,n3,1,…,nM,1]T即TDOA测量误差。由最大似然估计，可以确定目标函数为

minf(X)=(Gr-d)TQ-1(Gr-d)

(4)

可以确定目标函数的梯度矩阵

(5)

其中X=[x,y]T。为模拟Hesse矩阵性能，修正秩-1拟牛顿法所讨论的校正公式为

(6)

修正秩-1拟牛顿法解决了一般对称秩-1拟牛顿法Hk+1可能不是正定矩阵的问题。用迭代公式

xk+1=xk+αkdk

(7)

在实际使用时需先确定几个迭代初始条件。H1可使用单位矩阵，初始步长αk=0.15，迭代终止条件即误差容限为10-3。这1组参数可能不是性能最好的1组参数，但足够得到结果。在实验中尝试了几组参数，初始步长在0.15～0.75间取5组，误差容限取10-2，10-3和10-4。从实验结果来看，初始步长取0.6时可以取得较少的迭代次数。误差容限越小，迭代次数越多，但误差容限对结果的影响较小，仿真实验中误差容限选择10-3和10-4对结果精度并不造成太大影响，故选择误差容限为10-3。

2 超声波信号的产生

考虑到实验中使用的是普通的高音喇叭，接收端使用的是普通手机麦克风，由于手机麦克风的最高采样率一般为48 kHz，为了能够顺利接收高音喇叭发射的超声波信号，调制信号的超声波频率设置为20～22 kHz。实验中利用伪随机码的正交性来区别3个BS发射的信号。考虑到之前的带宽要求，使用511位且速率为511 bit/s的m序列，生成m序列的方法如图2所示。比较适合超声波信号的调制方式是二进制通断键控(On-off keying, OOK)调制或幅度调制。同文献[11]情况类似，这里没有使用BPSK调制，因为所使用的动圈式喇叭是利用振膜的振动发出超声波，设备可能无法实现相位的瞬变。OOK调制的载波频率设置为20 951 Hz，即码速率的整数倍。因此，超声波信号实际带宽为20 440～21 462 Hz。OOK调制后信号的旁瓣比较高，设计了五阶Butterworth带通滤波器进行滤波，滤波后信号即为可用于定位的信号。

3 超声波信号的同步

接收端接收到3个BS发射的超声波后需要对超声波信号进行同步。使用广泛应用于GPS软件接收机[15,16]的基于FFT的频域搜索算法来同步信号，这是一种能够较为快速地得到信号相关峰的算法，基于FFT频域搜索算法可以表示为

Rm=xn⊗C-n=F-1(F(x(n))F(Cn)*)

(8)

式中：x(n)为解调后的信号，C(n)为本地二进制伪随机码。计算所得R(m)中峰值(即相关峰的值)对应的采样点序号一般就是接收端从开始接收超声波到信号到达这一段时间内的采样点个数，该算法也可以用图3表示。

图3 基于FFT的频域搜索算法 Fig.3 Frequency domain block diagram based on FFT search

由于BS发射系统和MS接收系统的时钟不同步，将有可能产生时钟的偏差，从而使得接收的信号产生频偏。此外，在接收信号的过程中，如果MS发生了移动，也有可能由多普勒效应产生额外的频偏。因此，超声波接收系统还需要进行频偏估计。对于接收信号残存的频偏可以使用频率搜索法进行估计。设定好搜索粒度和范围，不断地改变本地载波的频率，再进行式(8)的运算，使得R(m)的峰值达到可接受的范围。这里R(m)的峰值可接受的阈值可以在实践中找一个合理的值。在同步时，如果输入信号和本地载波的相位差较大，也有可能无法得到正确的相关峰，这里使用相位搜索的方法来解决这一问题。相位搜索与频率搜索方法相差不多，是通过改变本地载波的相位来得到较好的相关峰。

4 实验结果与分析

4.1 仿真实验

在使用3个BS的条件下，对应用了修正秩-1拟牛顿法的定位算法进行了仿真。对经典的CHAN算法也做了仿真并比较了两种算法在精度方面的性能。仿真实验中使用蒙特卡洛方法来判断算法的性能。在仿真实验中，设想一个7 m×7 m的定位场景并假设测量误差的标准差从1 cm到11 cm。在仿真算法中发现，当选取的BS坐标绝对数值过大时，有可能因为初始点坐标位置的选取影响到算法的快速收敛。在实际实验中，如果BS坐标系过大，可以按倍率缩小其坐标的绝对数值。通过仿真实验发现，这样的预处理基本不会影响到最终结果的精度。在仿真实验中，每次在每个测量误差的标准差下生成1 000个随机点，通过定位算法估计出该点位置并计算其位置的RMSE。其测量误差标准差与估计位置RMSE的关系如图4所示。

由图4可知，在3个BS的情况下，两种算法在精确度上近似，可以满足室内定位的精度要求。

4.2 实物实验

在实物实验中，由于受限于房间大小和线缆长度，选取了(0, 0)，(0, 322.45),(236.85, 0)这一组坐标，坐标单位为cm。本实验主要使用的实验设备有YAMAHA RX-V375收音扩音机(即功放)和3个喇叭。喇叭前接电容或分频器。功放连接喇叭并控制喇叭发射信号，连接方式如图5。功放的最大发射功率调为-10 dB，此时功放的发射功率即为10 W。喇叭的放置如图6所示。通过普通智能手机接收喇叭发出的超声波并计算手机的位置。一共进行了7次测量，其手机实际摆放位置和测量估计的位置结果如表1所示。

图5 喇叭的连接 图6 高音喇叭的位置Fig.5 Connection of tweeters Fig.6 Position of tweeters

数据编号实际位置/cm测量位置/cm1(92.10 , 161.30)(92.42 , 162.45)2(65.50 , 215.20)(62.68 , 216.74)3(157.85 , 160.25)(156.84 , 151.34)4(39.45, 54.00)(41.05 , 56.60)5(131.50 , 188.50)(135.26 , 190.94)6(52.65 , 134.80)(55.09 , 132.73)7(65.75, 115.10)(63.29 , 113.45)

由表1数据计算可得，估计位置的RMSE为3.99 cm，最大误差8.97 cm。待定位设备与喇叭的距离会对定位精度产生一定影响。因为本系统是一个二维的定位系统，而手机麦克风的位置与3个喇叭不在同一平面。这样手机麦克风与喇叭的距离实际略高于理想状态下的距离，如果靠近某一喇叭则会加大这一因素造成的误差。

表2是本系统与其他一些系统的对比[10,11]。但文献[17]得到的精度与表2不太相同。从表2所示各系统的实验结果来看,本系统精度较高,且实验中仅使用普通手机麦克风接收定位信号。但本论文中的定位方案如果在更多的场景下或一些极限条件下做测试,实际精度可能稍低一些。如表2所示，Cricket系统的精度最高。成本方面，本文的实验中使用的功率放大器占了大多成本,在实际部署时也可不使用功放。文献[2]提到了其每个接收发射设备的成本为10美元左右。考虑到其部署成本，Cricket系统的成本应该比本文系统要高。

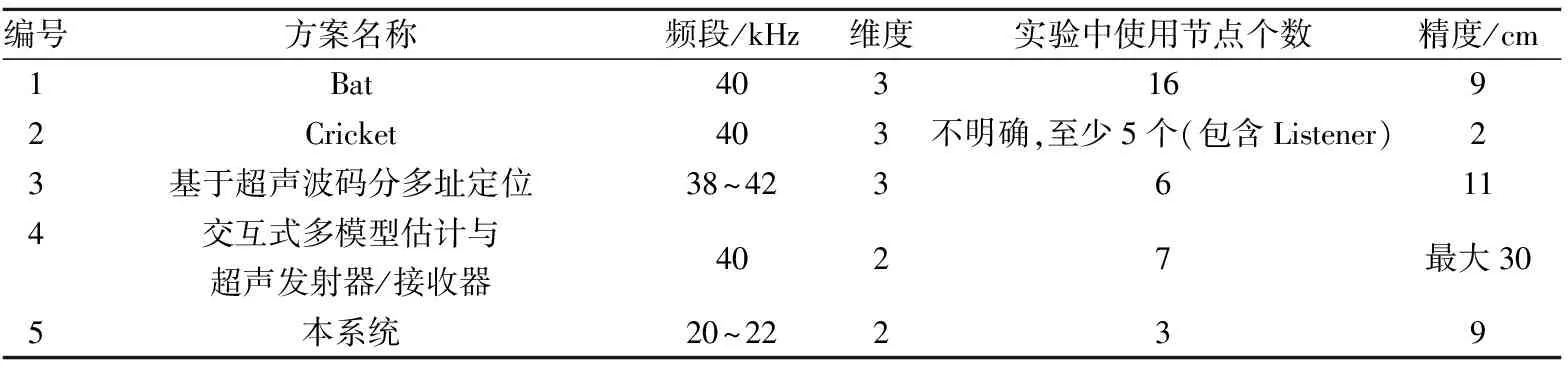
表2 各方案对比

5 结束语

本文介绍了一种基于TDOA低成本超声波定位方法，使用高音喇叭和手机麦克风实现了较高精度的定位。另外，本文还介绍了一种应用拟牛顿法得到MS位置估计的方法。仿真和实验结果表明，在有3个BS的情况下，拟牛顿法和CHAN算法的精度相近。在以后的实验中，将考虑加入更多的BS并实现三维定位。