OFDM系统群稀疏信道估计与译码迭代算法

李赛峰 付加飞 戚 婷 王 勇 叶中付

(1.中国科学技术大学信息科学技术学院，合肥，230027；2.电子工程学院电子制约技术安徽省重点实验室，合肥，230037；3.通信信息控制和安全技术重点实验室，嘉兴，314033)

引 言

在无线通信中，由于反射、绕射和衍射等因素的影响，接收端收到的信号是发送信号经过多条路径衰减和时延之后的叠加。为了从接收信号中更好地估计发送信号，必须进行信道估计。信道估计算法可以分为盲信道估计和数据辅助信道估计两大类。盲信道估计算法无需发送已知信号；而数据辅助信道算法则需要发送已知信号辅助信道估计。数据辅助算法的缺点是增加了系统开销，降低了通信效率。优点是性能优越。本文研究数据辅助信道估计算法。

在OFDM通信系统中，无线多径信道对信号传输的影响，可以用信号子载波上频率的复增益表示。因此，OFDM系统的信道估计算法在频域上处理非常简单高效。关于OFDM系统的信道估计算法问题，研究人员已经研究了很长时间[1-6]。经典的信道估计方法，比如基于最小二乘的信道估计算法，先通过导频估计出导频子载波信道响应，然后插值得到所有子载波信道响应。无论是线性插值还是多项式插值，采用的都是数值计算的方法，需要估计所有子信道的响应[7]。近年来，随着压缩感知(Compressive sensing，CS)理论的提出[8,9]，人们开始研究基于压缩感知的信道估计[10,11]。文献[10,12]指出，无线多径信道中，真正起作用的路径只有主要的几条。基于压缩感知理论的信道估计算法，通过时延划分构造出稀疏的路径衰减向量；然后将导频子信道响应作为观测值，通过求解一个带约束的优化问题来重构稀疏向量；最后，再利用重构出来的稀疏路径衰减和包含时延信息的冗余字典得到所有子信道响应。当导频信号数量一定时，与传统的插值方法相比，基于压缩感知的方法由于利用了信道的稀疏特性，需要估计的未知变量更少，所以估计效果更好。在接收系统中，在接收端对信号进行离散采样之后，延时抵达的各条路径信号，会扩散到信道时延附近的采样时刻上[13]。这样，无线多径信道呈现出群稀疏的特性[14]。相比传统的稀疏信道估计算法，利用群稀疏恢复算法来恢复信道响应，可以更加充分地利用信道的稀疏结构特性，从而提高信道估计的性能。Cotter和Rao利用无线信道的稀疏特性，提出了基于匹配追踪算法的频率选择性稀疏信道估计算法[15]，但是，该文没有提到压缩感知理论。Bajwa[10]和Berger[16]明确提出利用压缩感知理论估计稀疏信道。但是，没有涉及无线多径信道的群稀疏特性。Eiwen[14]提出了利用信道的群稀疏特性来估计信道，性能更好。但是，没有考虑将信道估计与译码算法结合。Huang[17]提出了稀疏信道估计与译码迭代算法，提升了信道估计的性能。但是没有利用信道的群稀疏特性，而且也没有考虑利用噪声功率估计来提高稀疏恢复的性能。

本文针对无线多径信道估计问题，提出了一种群稀疏信道估计和译码迭代解决方案。既利用了信道群稀疏的特性提高信道估计性能，又利用译码软信息，反馈到信道估计输入中，提高了接收系统的整体性能。同时，在带噪环境下的稀疏信号恢复算法中，利用译码反馈信号、导频信号和已估计的信道响应来估计噪声功率，进一步提高了稀疏恢复的精度。

1 系统模型

本文考虑循环前缀OFDM(Cyclic prefix OFDM，CP-OFDM)信号在无线多径信道中的传输。信号发送框图如图1所示，信源数据首先进行纠错编码和星座映射，然后经过串并转换，并加入导频信号，进行逆向快速傅里叶变换(Inverse fast Fourier transform,IFFT)变换，再添加循环前缀，最后进入发送设备。

图1 发送框图Fig．1 Block diagram of transmission

1.1 发送信号模型

对于CP-OFDM通信系统[18]，发送信号为

(1)

式中:sk为发送的符号星座点，k=0,1,…,K-1;K为OFDM符号的子载波数量；T为OFDM符号周期，Tg为循环前缀长度。每个OFDM符号最后(T-Tg，T)时间内的信号复制到OFDM符号最开始的位置，所以加入循环前缀之后，OFDM符号周期为：T+Tg。

1.2 信道模型

无线多径信道的冲击响应为[19,20]

(2)

式中:P(t)为路径数，ap(t)为第p条路径的衰减，τp(t)为第p条路径的时延。

假定信道在一个OFDM符号持续时间内保持不变，那么信道冲击响应可以简化为

(3)

那么，根据式(1,3)，忽略噪声的影响，发送信号进入无线多径信道信号的表达式为

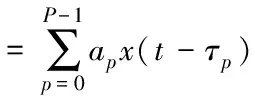
(4)

其中，⊗表示卷积运算。

1.3 接收信号模型

在信号接收端，对y(t)作串转并操作，然后FFT变换，最后再积分，就可以推导出第m(0≤m≤K-1)个子载波的表达式[21]为

(5)

综合式(1,4,5)，可以得到

(6)

对于所有的子载波，可以将式(6)写成

y=Hs

(7)

其中，y=[y0,y1,…,yK-1]T；s=[s0,s1,…,sK-1]T；H为信道状态信息矩阵，其元素为

(8)

2 基于群稀疏的信道估计

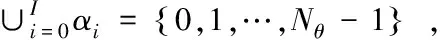
zθ=Φθ

(9)

根据压缩感知理论，应用稀疏恢复算法，可从低维度的观测向量zθ中恢复出高维度群稀疏向量θ。在真实的系统中，观测数据中包括了噪声信号。此处，假定噪声为均值为0，方差为σ2的高斯白噪声。那么，可以使用SPGL1[22]工具包中的Group-BPDN算法来恢复θ，即求解如下的优化问题

(10)

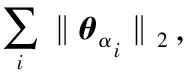
对比分析式(7，9)，基于压缩感知的信道估计，实质上就是对式y=Hs进行变换处理，构造出稀疏向量θ，然后根据信道特征和已知的发送信号(比如导频信号)，设计观测矩阵Φ，再根据观测值zθ，通过式(10)重构出稀疏向量θ，最后得到信道响应。

将式(8)代入y=Hs，可以得到

(11)

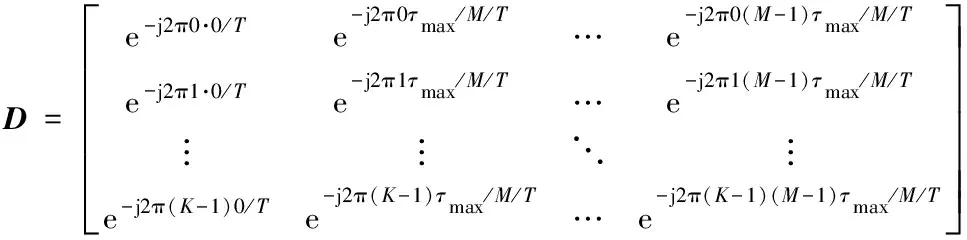
式中：Fp=diag(e-j2π0τp/T,e-j2π1τp/T,…,e-j2π(K-1)τp/T)，diag(·)表示一个对角线方阵，其对角线元素等于向量元素。利用多径信道的稀疏特性，构造基于时延的字典，字典的每一个原子，代表一条路径的时延，而需要恢复的稀疏向量就是每一条路径的衰减。根据文献[21]，表达式Fp中的信道时延划分为

τ=[0,τmax/M,2τmax/M,…,(M-1)τmax/M]

(12)

其中，M为时延划分的个数，也是字典原子的个数，τmax为信道可能的最大时延。

在式(12)中，字典原子个数远多于实际的路径数。所以，经过划分之后的路径时延和衰减都是稀疏的。而且，根据引言中提到的频谱泄露效应，它们都是群稀疏的。

为了估计信道响应，提取已知信号子载波数据，并综合式(8，11，12)，得到了基于群稀疏的信道估计模型得

y′=Hs′=DS′a

(13)

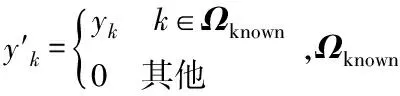
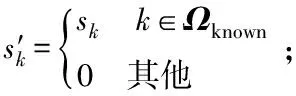
DS′构成观测矩阵，相当于式(9)中的Φ；

a是经过时延划分之后的衰减向量，a=[a0,a1,…,aM-1]T，即需要重构的群稀疏向量，相当于式(9)中的θ。这样，可以根据式(13)，利用观测值、字典和导频信号，通过Group-BPDN算法，恢复稀疏向量a。将式(13)的符号代入式(10)，就得到

(14)

其中，αi(0≤i≤I-1)是对集合{n|0≤n≤M-1}的划分，aαi是对向量a进行集合划分之后的子集。

最后，根据恢复得到的a和字典D，得到信道状态信息矩阵H为

H=Ddiag(a)

(15)

3 群稀疏信道估计和译码迭代算法

本文提出的稀疏信道估计和译码迭代算法，利用了无线多径信道的群稀疏特性，采用Group-BPDN算法估计信道响应。而且，将译码软输出结果返回到信道估计的输入部分，以迭代的方式提高了接收系统整体的性能。另外，提出了基于译码反馈信号、导频信号和已估计信道响应的噪声估计算法，更加准确地估计噪声功率，提高了稀疏恢复的精度。迭代算法的估计框图如图2所示。

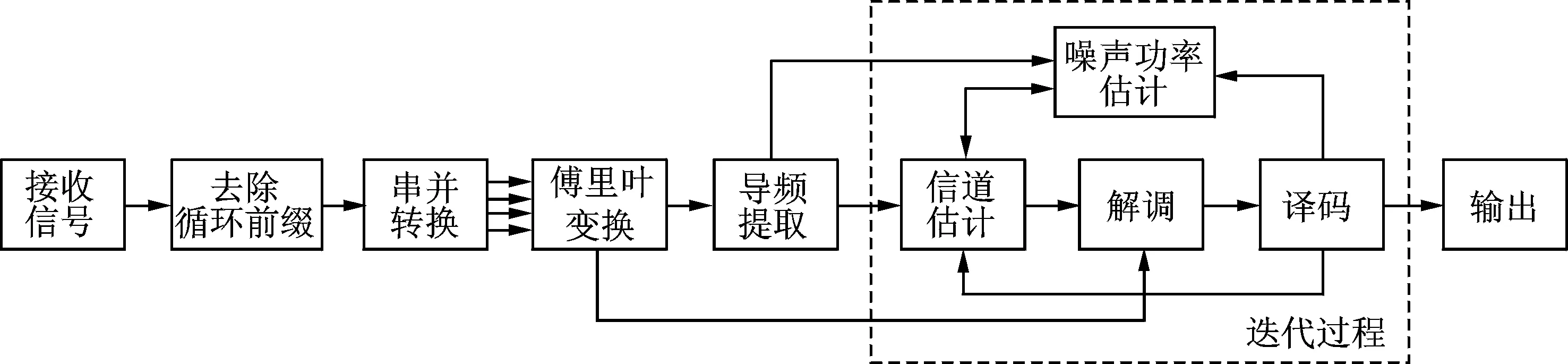
图2 群稀疏信道估计和译码迭代算法框图Fig．2 Block diagram of iterative algorithm of group sparse channel estimation and decoding

3.1 基于群稀疏的信道估计

在最初的信道估计阶段，将导频信号作为已知信号，即Ωknown=Ωpilot；由已知信号构成的对角矩阵S′，与基于时延划分之后的字典D，共同构造观测矩阵DS′。

在迭代的信道估计中，利用了译码输出的信息，反馈到信道估计的输入中，与导频信号一同构成已知信号，即Ωknown=Ωpilot∪Ωfeedback。译码输出信息相当于增加了已知信息，从而提高了信道估计的精度。

3.2 译码反馈机制

译码模块的输入为解调后信号，即经过信道均衡和星座解映射之后的信号。通过译码算法，得到软输出信息。在此，根据可信度对软输出信息进行排序，选择输出中可信度最高的部分数据，反馈到信道估计输入中去。返回到信道估计输入中的数据有两个作用:(1) 增加了已知信号集,这一点在3.1节中已有阐述;(2) 提高了噪声功率估计的精度。

在信道估计模块中，使用式(14)来恢复群稀疏信号。在式(14)中，噪声方法的设定将影响稀疏重构的精度。因此，为了提高算法性能，提出了利用译码反馈信号和已估计的信道估计响应来估计噪声功率的算法。

(16)

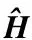
实际计算式(16)时，用时间平均代替集平均。通过译码反馈机制可以获得更多的y′和s′，从而提高估计的精度。

3.3 整体算法流程

群稀疏信道估计与译码迭代算法流程如下：

(1)信道估计前处理：去除循环前缀，FFT运算。

(2)开始迭代信道估计和译码迭代算法。

(a)初始化操作：设置最大迭代次数I，已知信号为导频信号，令Ωknown=Ωpilot，预置噪声功率，对稀疏变量的下标集合进行划分。

(b)根据已知信号和字典，计算观测矩阵DS′；根据已知信号子载波位置，设置观测值y′。

(c)根据式(14)，利用SPGL1工具箱重构群稀疏的信道路径衰减向量a。

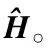
(f)将解调结果送入译码模块，输出译码的软信息。

(g)根据译码输出的软信息，对结果按照可信度排序，将最可信的λ部分的数据反馈回去，与导频信号一起构成新的已知信号，令Ωknown=Ωpilot∪Ωfeedback。

(i)如果达到最大迭代次数I，则退出迭代处理，跳到步骤(3)；否则，跳转到步骤(2(b))；

(3)根据译码数据，判决输出。

4 仿真实验

本文仿真了CP-OFDM信号在无线多径信道中传输的情况。OFDM信号的子载波数为256个，其中导频子载波数为32，均匀等间隔分布在信号子载波上。循环前缀的长度为OFDM符号周期的1/8。每个子载波信号的调制方式为QPSK。纠错编码方式分别为系统卷积码(2，1，3)和卷积码(2，1，6)。无线信道为瑞利衰落信道，路径数为7，多谱勒频率远小于1/T，其中T为OFDM符号长度。噪声为高斯白噪声。

在仿真中，字典原子数设置为256，即M=256。对稀疏变量划分为两个相邻的元素为一组，即J={(0,1),(2,3),…,(M-2,M-1)}。最开始时，噪声功率的初始设置为0.000 1(信号功率归一化为1)，在后续OFDM符号处理过程中，令噪声功率的初值为处理前一个OFDM符号时估计的噪声功率。最大迭代次数设置为6，第1次迭代后，令λ=10%，第2次迭代后，令λ=20%，第3次迭代后，令λ=30%，第4次迭代后，令λ=40%，第5次迭代后，令λ=45%，第6次迭代后，令λ=50%。

译码算法使用软输出的维特比译码算法[23]。

选择3种算法作为比较算法：

(1)基于最小二乘算法的信道估计[3]和译码迭代算法。

(2)基于一般稀疏信号恢复BPDN算法的信道估计[17]和译码迭代算法。

(3)基于群稀疏信号恢复Group-BPDN算法的信道估计和译码迭代算法，但是没有进行迭代的噪声功率估计。

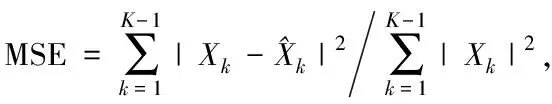
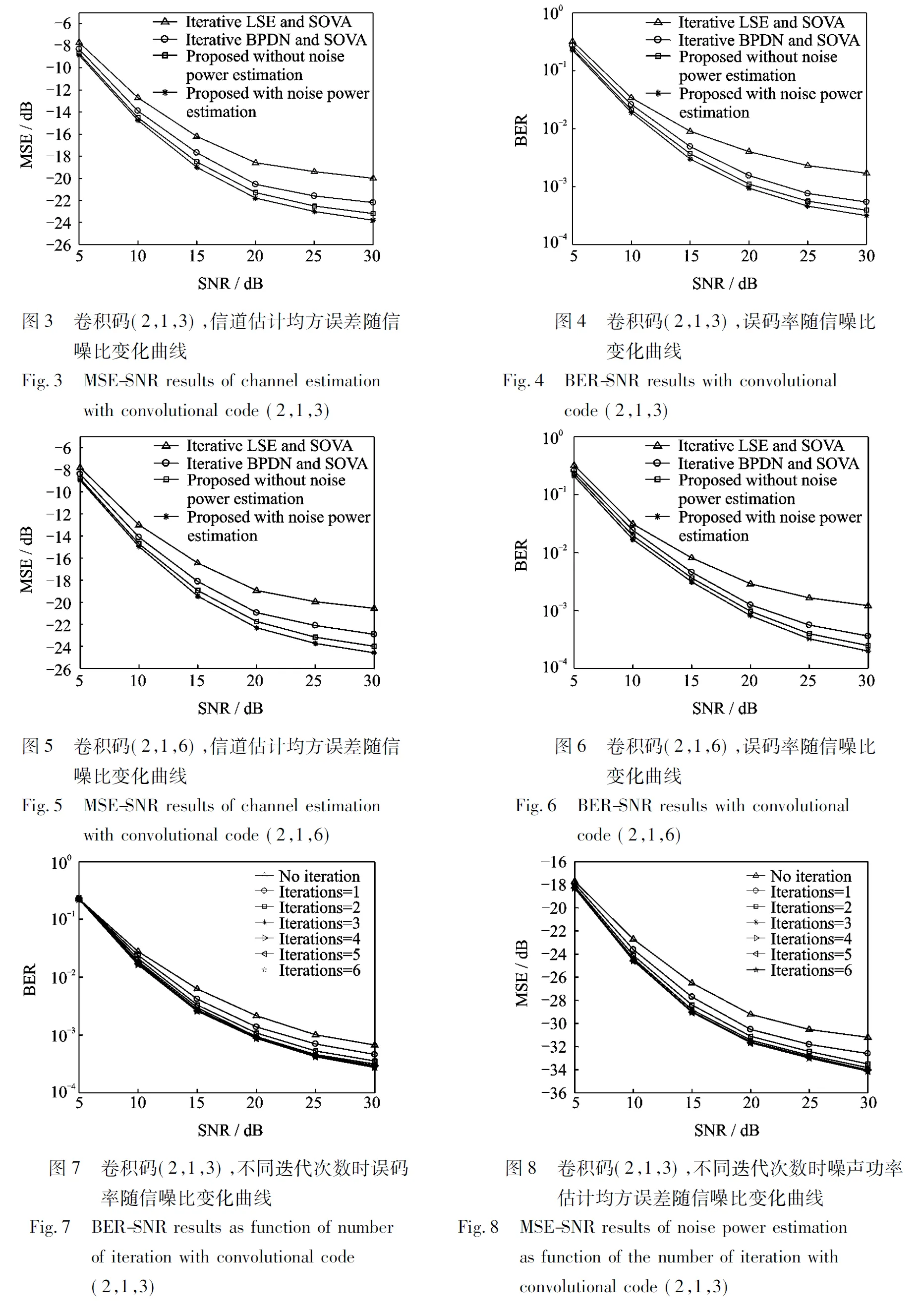
图3和图4分别表示采用卷积码(2，1，3)时，不同算法迭代3次时信道估计均方误差和误码率随信噪比变化情况。图5和图6分别表示采用卷积码(2，1，6)时，不同算法迭代3次时信道估计均方误差和误码率随信噪比变化情况。从图3—6可以看出，由于利用了信道的稀疏特性，基于稀疏恢复的信道估计算法性能都优于传统的最小二乘估计算法。深入挖掘信道的特性之后，基于群稀疏的信道估计算法优于一般的基于稀疏的估计算法。在基于信道群稀疏特性的估计算法中，估计噪声功率时的算法性能优于不估计噪声功率的情况。而且，从仿真结果来看，增加了卷积码的约束长度，性能提升了一些。图7表示采用卷积码(2，1，3)时，本文算法在不同迭代次数时的误码率随信噪比的变化情况。可以看出，迭代次数小于3次时，每增加一次迭代，误码率性能提高比较明显；迭代次数大于3次时，性能提高不明显。图8表示采用卷积码(2，1，3)时，不同迭代次数时噪声功率估计均方误差随信噪比变化的情况。可以看出与图7相似的情况，开始阶段增加迭代次数，噪声功率估计性能提升比较明显；然后再增加迭代次数后，性能提升非常有限。

由于信道译码部分的计算量相同，所以各类算法的计算复杂度的差异主要体现在信道估计部分。当采用线性插值时，对比算法(1)信道估计模块的计算复杂度为O(IK)，其中I表示最大迭代次数，K表示子载波数，可以看出此算法的计算复杂度较低。根据文献[24]可知，对比算法(2)和(3)信道估计模块的计算复杂度为O(IKM2)，其中M表示时延划分的个数，显然基于稀疏恢复算法的计算复杂度是比较高的；本文算法相对于对比算法(3)，增加了对噪声功率的估计，所以计算复杂度为O(IKM2)+O(IK)；可以看出，本文算法复杂度和算法(3)的复杂度相当。

5 结束语

如何消除信道对信号传输的干扰，一直以来都是通信研究的一个重点。在复杂的无线多径信道中，信号的畸变非常严重，信道估计的重要性更加凸显。本文针对无线多径信道的特性，提出了一种群稀疏信道估计和译码迭代算法。在信道估计中，利用了信道的群稀疏特性，挖掘了信道的结构化信息，提高了信道估计的性能。在信道估计之后，进行解调和译码，并把译码的结果根据可信度排序，将可信度较大的数据反馈到信道估计的输入部分，一方面增加了已知信号，因而提升了稀疏恢复的性能，另一方面，利用已估计的信道响应和译码反馈信号，结合导频信号，估计噪声功率，进一步提高了稀疏恢复的精度。通过实验仿真，比较了各种算法的信道估计均方误差和误码率。从仿真结果可以看出，本文算法采用联合迭代机制，充分利用了信道的群稀疏特性和译码带来的处理增益，性能最好。