时域欠采样线性调频信号参数估计方法

冯浩然，阮怀林

（国防科技大学电子对抗学院，合肥 230037）

0 引言

作为活跃在电磁频谱空间一种常见的非平稳信号，大时宽带宽积和低截获率的特性使得线性调频（LFM）信号在雷达、通信等工程领域内具有十分广泛的应用，对其参数的精确估计是雷达信号侦察和数据处理领域十分重要的课题之一。而较宽的工作带宽给雷达侦察系统带来的不仅是较高的采样频率，更是增加了系统硬件实现的难度，难以在奈奎斯特采样条件下满足其时域参数估计的要求。用较低的采样频率对空间入射信号进行处理不失为一种较为现实的方法。然而，对较低的采样率进行欠采样估计容易造成频谱混叠，产生测量模糊值，无法较为真实地估计出原始信号的信息。因此，寻求一种行之有效的解模糊方法成为欠采样环境下参数和波达方向估计技术的关键。

M.D.Zoltwoski等[1]于1994年提出的在采样环境下的频率和波达方向联合估计的算法，无疑是一种比较成功的算法，但是该方法需要给各阵元配备滤波器和混频器，增加了硬件成本和运算量。文献[2]建立了一个无模糊的采样模型和阵列结构，基于MUSIC算法，同时利用多个采样通道和快拍通道进行参数估计，克服了时空欠采样下的估计模糊问题，降低了运算的复杂度。文献[3]利用中国余数定理（CRT，Chinese Remainder Theorem）的重构特性，对欠采样环境下多个信号入射情况进行频率和方位角的联合估计，方法具有较好的稳健性。

本文基于文献[4]时延共轭相乘的思想，结合CRT解模糊的特性，提出在时域欠采样环境下对线性调频信号调制斜率和初始频率无模糊估计的方法。欠采样环境下，接收信号经过功分器，通过三路不同频率欠采样，其中两路经过延时共轭，与采样后的信号相乘得到异频正弦信号，基于ESPRIT旋转不变特性建立矩阵束，对得到的正弦信号进行处理，根据中国余数定理求出原始信号调制斜率的估计值。再根据估计出的调制斜率合成数字信号对后两路采样信号进行解线调，然后对该两路信号进行快速傅里叶变换和谱峰搜索估计出初始频率相对于采样频率的余数，结合余数定理估计入射信号的初始频率。经过仿真验证，本文提出的算法能精确地估计出线性调频信号的调制斜率和初始频率，在较低信噪比情况下仍有不错的效果。

1 欠采样系统模型

本文提出算法框图由图1表示。

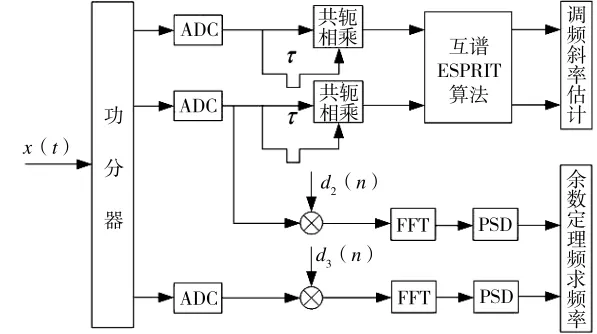
图1 线性调频信号参数估计框图

假设有空间入射信号x（t），其频率在频域区间[fmin，fmax]分布，信号由线性调频信号和噪声构成

其中，f0代表信号的初始频率，k是信号调制斜率，A是信号幅度，φ是信号初相，假设v（t）是与信号相互独立的零均值高斯白噪声。

经过功分器，其中各路信号用不同采样率进行欠采样得到信号x1（n），x2（n）和x3（n），

将经过欠采样的信号x1（n）和x2（n）同时进行相同延时，得到两路经过时延的信号取共轭与x1（n）和x2（n）相乘得到了两路异频正弦信号。结合旋转子空间不变（ESPRIT）方法，较为精确地估计出接收信号的调制斜率kˆ。利用调制斜率的估计值kˆ合成数字信号d2（n），d3（n），分别对信号x2（n），x3（n）解线调得到z2（n），z3（n），经过快速傅里叶变换（FFT）和谱峰检测（PSD），利用改进Rife算法和Quinn算法，无模糊估计出信号x（t）的原始频率。系统流程如图2所示。

图2 算法流程图

2 欠采样宽带线性调频信号参数估计

2.1 调制斜率估计

根据本文提出的算法，对接收到的线性调频信号，通过功分器后，其中两路用采样率fs1和fs2对信号进行欠采样（fs1，fs2＜B=kT，B 为信号带宽，T 为信号脉宽），得到信号x1（n），x2（n）。将信号x1（n）和x2（n）同时延时，得到

其中两路经过时延共轭相乘得到的正弦信号

其中，

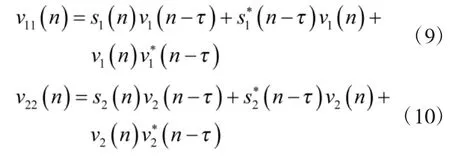
令

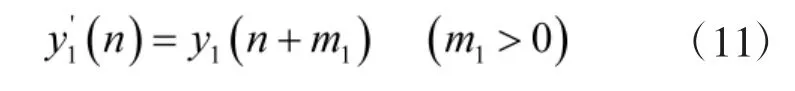
有y1（n）和y1'（n）的互相关函数

由于v1（n）是与信号相互独立的零均值高斯白噪声，且v11（n）均值为0，有

在单信号入射情况下，构造如下P×P维的互相关函数矩阵

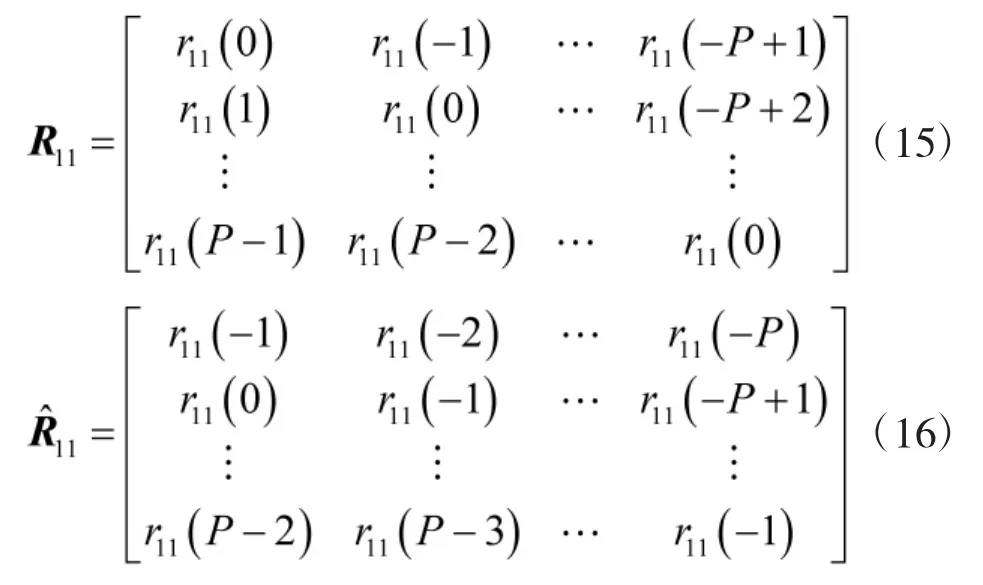
显然，根据中国余数定理，有模糊信息的信号频率如下

其中，arg表示取相角，floor表示向下取最大整数。考虑噪声影响，有

2.2 初始频率估计

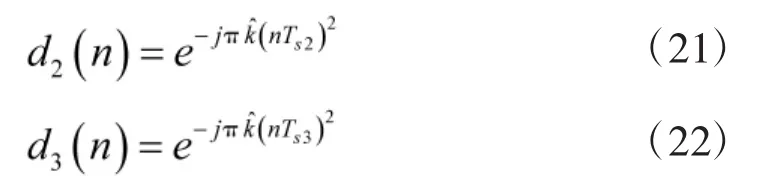
采样率依次为fs2，fs3。用合成的数字信号对x2（n），x3（n）解线调，有

从式（26）和式（27）容易看出，z2（n）和z3（n）都含噪声正弦信号。对得到的正弦信号进行快速傅里叶变换和谱峰搜索，得到f0对fs2和fs3的余数，即

式中，k2、k3都是正整数，则把求解频率f0转换为通过对余数 F2、F3的估计，即

F2和F3是低速采样后进行FFT的结果，本文采用改进的Rife算法和Quinn算法[6]相结合的方法对频率余数F2，F3进行估计，并根据估计出的余数估计，从而估计出一个比较精确的频率值。方法中，对（zn）的N点FFT，记作Z（k），将Z（k）的最大谱线位置记作l0，其幅值为；次大谱线位置记作l1，幅值为。其中，，有F与之间的相对偏差。

低速采样频率估计具体实施步骤如下：

5）对z（3n）进行相同处理估计出；

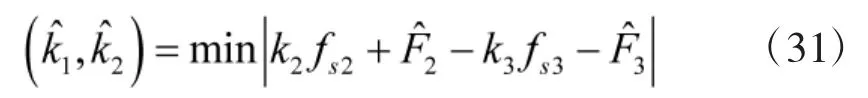
8）根据，无模糊估计出信号频率

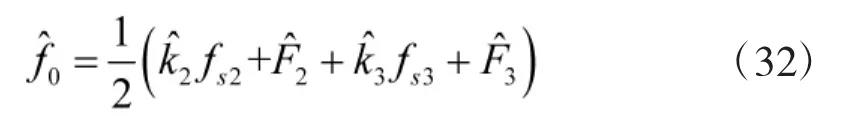
2.3 参数设置

由于y（1n）和y（2n）都是频率为k的含噪声复正弦信号，则接收信号的调制斜率k的估计精度和时延的选择有关。若选择的值较小时，对k估计产生的误差将对k值估计精度产生较大影响；若选择的值较大时，会造成y（n）数据长度变短，增大了对频率k估计的难度。选择一个合适的时延opt十分有必要。由于经过信号时延共轭相乘得到的频率为k，该信号的频率估计误差的CRB反比于（T-。因而选择，即。如果LCM（fs1，fs2）＞0.4B，则可实现调制斜率无模糊估计。

另外，两路合成信号的采样率fs2，fs3也不能随意决定。对于要进行FFT和PSD的两路信号，为了满足快速处理数据的需要，两路信号采样率相差不宜过大，较大的频差容易增大调试难度，降低频率估计的运算速度；同时，由于对信号频率估计会产生误差，为后期处理中国余数定理求解的方便，采样率不宜过于相近，频差要选择稍大于估计中可能产生的误差值；另外，fs2，fs3的选择要适中，较高的采样率无法实现对硬件成本的降低和数字处理压力的缓解，而较低的采样率会增大对信噪比的要求[8]。特别注意要根据无模糊测频感兴趣的频域范围，决定采样率 fs2，fs3。

3 仿真分析

为了验证欠采样环境下线性调频信号调制斜率估计和初始频率估计算法的有效性，作了如下仿真实验。假设有空间入射信号，其中，A=1，f0=9.375×109Hz，k=58 MHz/μs，φ=0°。设置采样率fs1=230 MHz，fs2=200 MHz，fs3=210 MHz；设置脉宽 T=25 μs，带宽 B=1.45 GHz，时延。易得，频率的不模糊估计区域为4 200 MHz。设文中感兴趣的频率区域为[8，12.0]。对本文提出的方法进行仿真验证。

下页图3、图4分别是在信噪比为-5 dB情况下，直接对信号进行估计和利用本文提出方法进行相关参数估计的仿真结果。

可以看出，由于对宽带信号进行欠采样，直接进行参数测量和估计，会存在很大的毛刺和估计误差问题。而经过余数误差的修正和线性拟合，利用本文提出的方法对初始频率进行估计，使得瞬时频率有很好的线性效果，测量结果比较清晰。虽然在-5 dB时调制斜率估计存在一定的误差，但初始频率的估计仍有不错的效果。

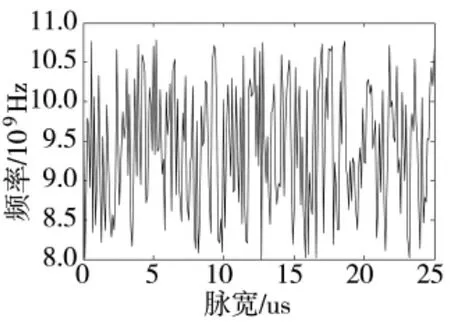
图3 直接进行频率估计的估计频率

图4 -5 dB经过余数修正和线性拟合的估计频率

图5（a）、图 5（b）表示进行初始频率估计时，z（2n），z（3n）支路对采样率fs2，fs3的频率余数的测量结果。

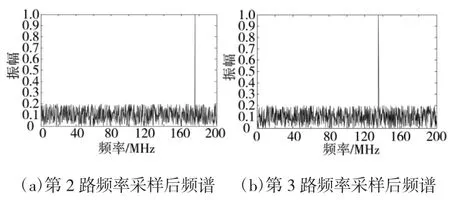
图5 频率采样后频谱图

能够比较清晰地看出，两路信号得到的频率余数的估计值分别是，根据已知的频率区域范围，可以对（k2，k3）进行估计，其估计值为，因而得到无模糊估计出信号初始频率

在信噪比为-5 dB情况下，初始频率估计值与原信号值有0.22 MHz的估计误差，相对误差为0.23×10-3，调制斜率的估计值与原始信号有不到1/1 000的估计误差。

图6、图7是300次蒙特卡罗实验信号调制斜率和初始频率估计结果随信噪比增大的均方根误差变化曲线。

可以看出，在信噪比过低时，根据本文提出先估计调制斜率然后估计初始频率的特点，在已有噪声干扰的基础上，同时存在有误差的调制斜率估计值的影响，使得在估计初始频率时有与原始值之间存在较大的估计偏差。随着信噪比的提高，调制斜率估计值将无限接近真实值，初始频率估计值的准确度随之增高。随着信噪比的提高，噪声对估计结果的影响越来越小。

图6 调制斜率估计的均方根误差曲线

图7 初始频率估计的均方根误差曲线

4 结论

针对线性调频信号带宽较宽，进行信号采样困难和数据处理压力较大的情况，本文提出在时域欠采样下对线性调频信号进行调制斜率估计和初始频率估计的方法。方法运算量较小，对宽带线性调频信号的参数估计有较高的精度，易于硬件实现和降低成本，仿真验证了本文所提方法的有效性。同时，在较低信噪比情况下，本文所提方法仍具有较好的性能，具有工程应用价值。