非对称双原子分子在输运扩散中的取向效应∗

江智亮 陈沛荣 钟伟荣† 艾保全 邵志刚

1)(暨南大学物理系,思源实验室,广州 510632)

2)(华南师范大学物理与电信工程学院,广东省量子工程与材料重点实验室,广州 510006)

(2018年7月17日收到;2018年9月29日收到修改稿)

1 引 言

非平衡输运作为统计物理中的一个重要的研究领域,一直受到研究者的关注[1−6].近年来,多原子分子的结构对其输运的影响,受到研究者的重视.2012年,Romer等[7]发现由一大一小的两个原子组成的分子,在温度梯度作用下,分子的取向并不是完全无序的,而是小原子会更趋向低温的一侧.该研究组将这种现象称为“热分子取向效应”.随后人们开始对热分子的各种特性进行了一系列研究.Lee[8]确定了粒子的尺寸各向异性、分子体积比等与取向的关系.Tan等[9]认为粒子的纵横比影响取向的难易程度.Gustavsson等[10]发现在湍流场中粒子也有取向行为.Kiharu和Him[11]认为热流是影响取向的主要因素.Peter等[12]报道在热不均匀系统中也有类似的取向行为.Christopher等[13]通过引进均匀力场构造浓度差,研究浓度梯度和温度梯度的影响.

以上大部分研究均认为温度梯度是分子取向的主要因素,取向参数与温度梯度成正比,并借用熵产生率公式计算出两者的关系.根据非平衡统计物理的线性响应理论[14],完整的昂萨格熵产生率公式共有两项,一项与温度梯度有关,另一项与化学势梯度有关[15].本文对该热分子取向现象的进一步跟进中,发现当系统温度较低时,化学梯度也可以导致分子的择优取向.有趣的是,化学势梯度驱动的系统与温度梯度驱动的系统,其中分子的取向性是相反的.因此说明仅从温度梯度的角度来解释分子取向的原因,并没有真正揭开其真实的物理机制.Christopher等[13]虽然研究了类似化学势梯度的影响,但是该研究只是粗略研究浓度梯度,并将浓度梯度的影响抽象为一个固定方向的力.显然,这并非是真正的浓度梯度或化学势梯度.为弥补化学势梯度研究的空缺,本文拟同时从温度梯度和化学势梯度出发,研究分子的取向效应,并分析产生这种现象的更深层次的原因.

2 模型与方法

如图1所示的二维非平衡系统,蓝色实线是系统的边界.ABCD和EFGH分别是左右粒子库,在本文中左右粒子库的尺寸为:AB×AD=10.5 nm× 10.5 nm,连接左右粒子库的通道长度为L,宽度为d.黑点和红圈是一个分子的两个原子,红的是大原子M,黑的是小原子N,分子的取向rMN是以M原子为起点,N原子为终点,分子取向与水平方向Z正方向的夹角为θ,⟨cosθ表示对所有粒子夹角的余弦求和,⟨cosθ=0表示分子取向均匀,⟨cosθ/=0表示有取向偏好. 由于分子本身的参数包含了质量以及Lennard-Jones参数中的σ和ε等多种参数,因此选择用什么标准来恒定原子的大小会涉及复杂的参数选择.结合前人的研究[7]以及σ参数的意义,这里只选择σ参数来衡量原子的大小.为了遵循控制变量法的原则,本研究中涉及的原子与真实原子有所区别,一般以He原子为基础定性化模型,图中的N原子就是He原子,通过σ参数增加得到大原子M,再构成分子MN,当然这样的分子未必真实存在,但是能反映实际中类似结构的分子或者分子团.因此本研究中的大原子和小原子并不是传统意义的大小原子,这里的大小原子是对一种独立粒子或粒子团的简化,具有普遍性.

图1 二维模型示意图 通道参数L=10 nm,d=6 nm;黑点和红圈为双原子分子,红色表示大原子M,黑色表示小原子NFig.1.Diagram of two dimensional modle.Channel parameters:L=10 nm,d=6 nm.Black dots and red circles are diatomic molecules.Red represents large atoms M,black represents small atoms N.

本文采用分子动力学计算粒子的运动过程,使用蒙特卡罗的方式来控制保持左右粒子库的粒子数量[5],左右粒子库浓度分别为CL和CR.温度的控制采用Langevin随机热库来实现,温度分别为TL和TR,通道不与热库接触.当单独对浓度梯度控制时,整个系统都放在同一个热库中,这时整个系统温度一致.如(1)和(2)式所示,不同分子之间的范德瓦耳斯作用使用Lennard-Jones模型来描述[16,17],

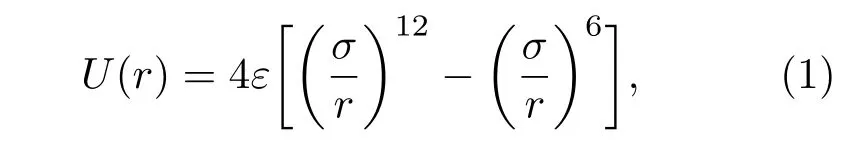
其中r是两个粒子之间的距离,ε和σ是同一类粒子之间的Lennard-Jones参数.对于两种不同类的粒子(A粒子和B粒子)之间的参数由下式确定:

同一分子内部双原子一般是抽象为简谐振子模型[18]:

其中,KAB为A,B原子间的相互作用常数,r0为A,B原子的平衡间距.本文中,系统边界均设置为软墙,粒子与墙的相互作用为Lennard-Jones形式:

在这里,势能参数εw和σw分别取碳原子与所研究的粒子的参数[19].分子运动的朗之万方程:

其中,r是坐标,mi是第i个粒子的质量,Uall是粒子相互作用包括以上所有作用势的总和,η(t)是高斯随机噪声,强度为2kBΓT,Γ是粒子的摩擦系数,T为系统的温度.对(5)式采用Verlet算法进行数值计算,步长选取0.055 fs.粒子库的浓度保持采用蒙特卡罗算法,具体可以参考文献[20—22]的做法.由于分子取向效应具有强烈的统计物理特征,为了获得更加稳定的数据,本研究采用长时间(步数109)多次计算(30次),然后取平均的方式来获取最后的结果.

粒子流的计算是根据从两边粒子库与通道交换粒子数来确定.比如,在整个计算过程中(时间为t),从左边粒子库进通道净粒子数为N1,从通道进右边粒子库净粒子数为N2,当t足够长,N1/t和N2/t将趋于稳定值.如果N1/t=N2/t那么可以认为系统达到稳定态,这时系统的粒子流Jn=N1/t=N2/t.

3 结果与讨论

如图2所示为化学势梯度和温度梯度对分子取向效应的影响.从图中可以看出,化学势梯度和温度梯度都对分子取向效应有影响,并且梯度越大,取向效应越明显.但是化学势梯度和温度梯度对该效应的影响是相反的.在化学势梯度之下,如图2(a),分子取向效应表现为大原子更趋向于低浓度粒子库的方向,而小原子更趋向于高浓度粒子库的方向,分子取向与流(粒子流或热流)的方向相反,表现为⟨cosθ>0;在图2(b)中,⟨cosθ<0,说明在温度梯度之下,分子取向效应表现为大原子更趋向于高温粒子库的方向,而小原子更趋向于低温粒子库的方向,分子取向与流的方向相同.由于本文研究的体系可近似于理想气体,这里化学势梯度的计算公式为∇µ=RT(lnCL−lnCR)/L,R为气体常数;温度梯度计算公式为∇T=(TL−TR)/L.

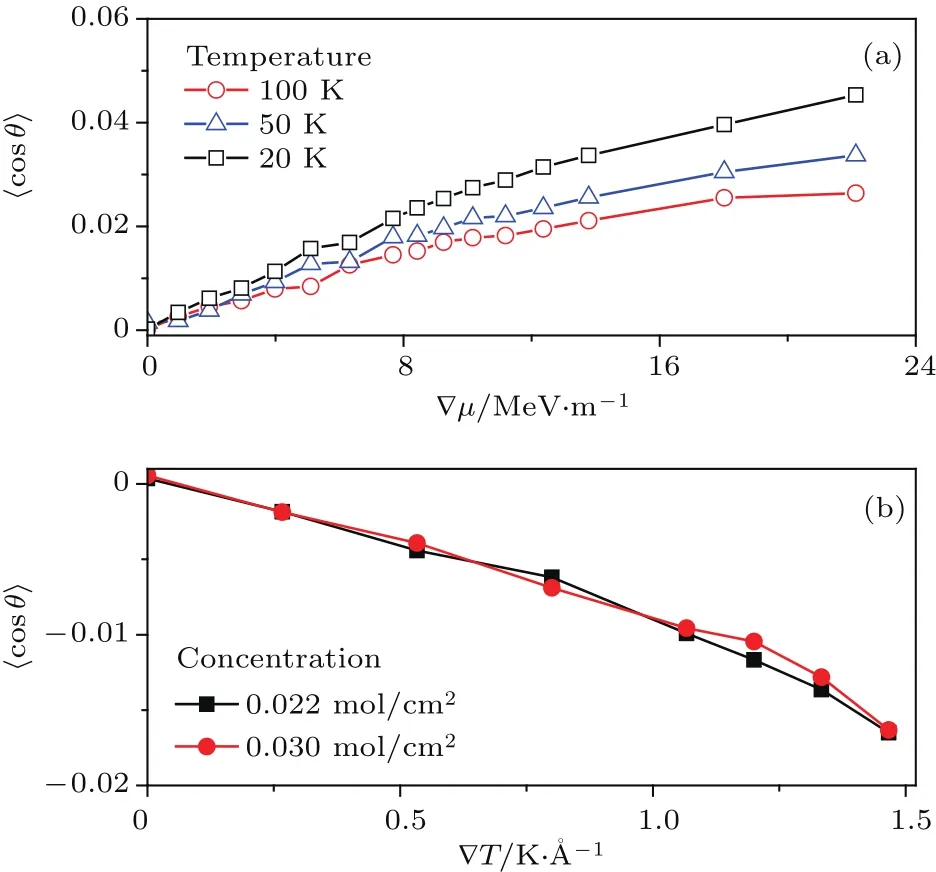
图2 化学势梯度(a)和温度梯度(b)对分子取向的影响分子参数为 σB/σA=2.2, εB/εA=1,mB/mA=1;其他参数:(a)∇T=0,体系的平均温度分别为20,50和100 K;(b)∇µ=0,体系平均浓度分别为0.022,0.030 mol/cm2Fig.2.Influence of chemical potential gradient(a)and temperature gradient(b)on molecular orientation.Molecular parameters: σB/σA=2.2, εB/εA=1,mB/mA=1.Other parameters:(a)∇T=0,the average temperature of the system is 20,50 and 100 K respectively;(b)∇µ=0,the average concentration of the system was 0.022,0.030 mol/cm2,respectively.

由于化学势梯度与温度梯度对取向方向的影响刚好相反,这种现象类似于电子的自旋磁矩的取向:向上或向下.我们知道,磁矩的取向一般可以用双稳态模型来描述.这里,我们借用双稳态模型,假设当分子处于平衡位置,其取向函数⟨cosθ=0,在梯度场作用下其偏离平衡位置,可能演化到另两个稳定态.如果假设n=⟨cosθ表示偏离量,那么可以用双稳函数来表示其能量:En=−C1n2/2+C2n4/4,其中C1和C2分别为取向偏好的难易程度.取向偏离的能量变化率为:∂E/∂t=(−C1n+C2n3)∂n/∂t. 在化学势梯度与温度梯度作用下,熵产生率为

其中Jq和Jm分别表示热流和质量流.根据线性响应理论,对应的线性流力方程为

其中Lij表示第j种力产生的第i种流的唯象系数.在稳定态时,∂n/∂t=0,根据图2的结果以及n=,可以得到:

说明温度梯度与取向参数成正比,化学势梯度与取向参数成幂指数关系.(8)式也反映了化学势梯度与温度梯度对取向方向的影响是相反的.对于既有浓度梯度,又有温度梯度的情况,浓度梯度和温度梯度对分子取向效应的影响表现为竞争关系.从图3可以发现,在∇µ=0时,⟨cosθ的符号始终是负,分子取向效应的方向在不同的温度梯度下是一致的.而当∇µ>0时,随着∇T的增大,分子的取向发生了方向翻转.

这里有一点值得指出,如图3箭头所示∇T=1.12和1.68 K/A时,⟨cosθ=0,分子没有偏好取向,但此时体系的热流分别为Jq=0.06和0.14 eV/ns,体系的质量流分别为Jm=0.46和1.10×10−14mol/s.这也间接说明了热流和质量流并非是产生分子取向的主要原因.

以上是外界条件对分子取向效应的影响,分子取向效应存在的自身条件是分子本身的非对称性对其取向效应的影响至关重要.从图4中可以看出,分子本身的非对称性(σB/σA)越大,分子取向效应越明显,当σB/σA>1.6,分子本身的非对称性对取向效应的影响逐渐饱和;当σB/σA=1时,即对称分子,此时即使温度梯度或者化学势梯度并不为零,⟨cosθ=0,也不存在分子取向效应.需要说明的是,当σB/σA>1.6时,结果有一些波动.原因在于随着σB/σA增加,分子大小在增加,相互作用有效间距在增加,在体系尺寸不变的前提下,计算的误差也在增加.也因此我们不再考虑σB/σA>2.2的情形.

图3 化学势梯度和温度梯度共同影响下的分子取向 分子参数与图2相同;其他参数:高温粒子库的化学势高,低温粒子库的化学势低(化学势梯度和温度梯度方向相同)Fig.3. Molecular orientation under the combined influence of chemical potential gradients and temperature gradients. The molecular parameters are the same as in Fig.2.Other parameters:the hightemperature particle library has a high chemical potential and the low-temperature particle library has a low chemical potential(chemical potential gradient and temperature gradient in the same direction).

图4 在温度梯度场中分子的非对称性与分子取向的关系Fig.4.The relationship between molecular asymmetry and molecular orientation in a temperature gradient field.

4 结 论

本文从非平衡统计物理的基本理论出发,采用分子动力学和蒙特卡罗方法探讨非平衡条件下非对称双原子分子的取向问题,考察了影响分子取向的各种因素,旨在揭示非平衡输运中双原子分子取向的更深层次的物理机制.

研究表明,温度梯度、化学势梯度、分子非对称性对分子取向效应有影响.本文将原来只包含了温度梯度的结论公式推广到适用于温度梯度和化学势梯度的完整关系式:

其中σBA= σB/σA,表示分子的非对称性.根据(8)式,这里α=1,β=1/3,并且有f<0,g>0;对于对称粒子,f=0,g=0.

从本文结果可以得出,导致分子取向效应的原因分为两个方面:第一是分子的非对称性,分子本身非对称性越大,越有利于产生分子取向效应;第二是外界条件,包括化学势梯度、温度梯度等,化学势(温度)梯度越大,分子取向效应越明显,化学势梯度和温度梯度对分子取向方向的影响是相反的,其表现为竞争关系.必须指出,(9)式只考虑了一个最基本的非对称分子和系统.对于影响取向效应涉及的其他因素,比如质量不对称、相互作用类别不同、分子内部非线性相互作用等需要更深入地研究.