基于势流理论的回转体并联入水双空泡演化动力学研究∗

宋武超 魏英杰 路丽睿 王聪 卢佳兴

(哈尔滨工业大学航天学院,哈尔滨 150001)

(2018年7月17日收到;2018年9月11日收到修改稿)

1 引 言

运动体以一定的速度撞击自由液面,将自身动能传递给了附近水域,引起流体质点向运动体外侧运动,致使空泡敞开及自由液面喷溅,形成入水空泡.作为典型跨界质过程的入水过程,涉及运动体、空气和水三者的耦合作用,具有高度非线性和非定常性,运动体的运动特性和流场特性都极为复杂.

早在19世纪末,Worthinghton和Cole[1,2]利用闪光摄影技术对球体等垂直入水时产生的入水空泡进行了大量的试验研究,并对入水空泡流动现象做了开创性的描述.二战以后,在美国海军支持下,学者们针对入水过程开展了系统性的试验研究工作,其中代表性的有Waugh[3],Birkho ff和Caywood[4],Glibarg和Anderson[5]以及May和Woodhull[6]等.21世纪以来,随着试验设备、测量技术的革新,从运动体入水过程的试验中获得的信息更加全面,为入水空泡流体特性的研究提供了更加有效的方法和途径[7].Holfeld等[8]和Tabuteau等[9]分别在微重力、不同黏度液体等特殊条件下开展了入水实验研究.对于入水空泡形态预测的理论方法,Logvinovich[10]首次提出了基于能量守恒定律的空泡独立膨胀原理,为之后空泡发展理论研究提供了重要基础.Lee等[11,12]基于能量守恒定律,提出了描述高速入水空泡形态发展演化的理论方法,对入水空泡扩展、收缩和闭合过程进行了较为精确的描述.Truscott[13]将Logvinovich提出的独立膨胀原理进行了扩展,准确地预测了运动体倾斜入水过程中入水空泡形体的演化规律.Yan等[14]基于势流理论建立了低速入水空泡动力学模型.Gordillo等[15]采用势流理论推导了高雷诺数入水条件下空泡闭合点流动特征.Aristo ff和Bush[16]同样基于势流理论得到了入水空泡形态的理论解.国内方面,叶取源[17]基于欧拉-拉格朗日混合边界元法,求解获得了圆锥垂直入水过程中入水空泡形成、发展以及闭合的变化规律.路中磊[18]基于Yan等[14]的分析方法,建立了适用于开放空腔入水空泡波动预测的理论模型.张阿漫等[19]基于势流理论分析了气枪气泡远场压力子波特性.

在现有关于入水空泡动力的研究中,多以单个运动体入水所形成入水空泡的动力学特性作为研究重点,主要考虑了空泡的演化过程,并对其流动方式进行了简化,形成了较为完善的单独低速轴对称入水空泡动力学计算模型.然而,对于双运动体入水过程所形成的入水空泡的动力特性,尚无人涉及.双回转体入水过程中所形成的入水空泡,呈现出了较强的非对称性;两回转体轴线内侧区域空泡演化过程中,流体形成了相对流动,从而使得流动不再具有轴对称特性,而发展成复杂的三维流动,且具有强非线性,使得理论模型的建立难度更大.

本文首先简要介绍单独入水空泡与并联入水空泡各自的演化特性;而后基于势流理论,在现有的单独入水二维轴对称计算模型的基础上,将并联入水过程中空泡之间的扰动简化为扰动速度势,给出扰动最强区域的空泡演化扰动模型;基于非线性假设,引入三维影响函数,通过影响函数建立空泡自由扩张区与扰动扩张区的过渡关系,得到三维非对称空泡演化计算模型,并基于该模型分析同步并联入水过程空泡形态的三维演化特性.

2 单独入水空泡与并联入空泡演化特性分析

2.1 实验系统与模型参数

试验系统由试验水槽、光学测试系统和释放机构三部分组成,如图1所示.试验水槽采用尺寸为300 mm×300 mm×900 mm的小型水槽,水槽四壁为钢化玻璃,壁厚10 mm,槽底垫有缓冲橡胶垫,防止射弹入水对缸体造成破坏.试验光源采用4盏发光二极管(LED)作为背景光,并用柔光屏对背景光进行柔化,使背景光均匀撒布,以达到良好的拍照效果;采用2盏LED灯作为顶光,以增强空泡内部光照条件,进而增强圆柱体边界清晰度,便于图片数据的后期处理.圆柱体运动过程通过Photron FASTCAM SA-X型高速摄像机采集,并通过自编程序对运动轨迹及运动姿态进行提取,以获得圆柱体运动特性.相机采集帧率为2000 fps,相机上安装广角镜头,以扩大视野,捕捉更多运动信息.

释放机构由推拉式电磁铁和竖直导轨组成,如图2所示.其中竖直导轨起导向作用,以确保试验模型入水时保持竖直姿态;推拉式电磁铁通过触发开关控制,共用同一个电信号,以确保触发的同步性.当电源接通时,电磁铁推拉杆同时收缩,释放模型.为防止电磁铁收缩引起的支架振动对释放产生影响,导轨和电磁铁分别安装在不同的支架上,导轨支架和电磁铁支架相互独立.

试验模型如图3所示.模型直径D=10 mm,长L=60 mm,模型采用6063铝合金加工,密度为2.7 g/cm3.

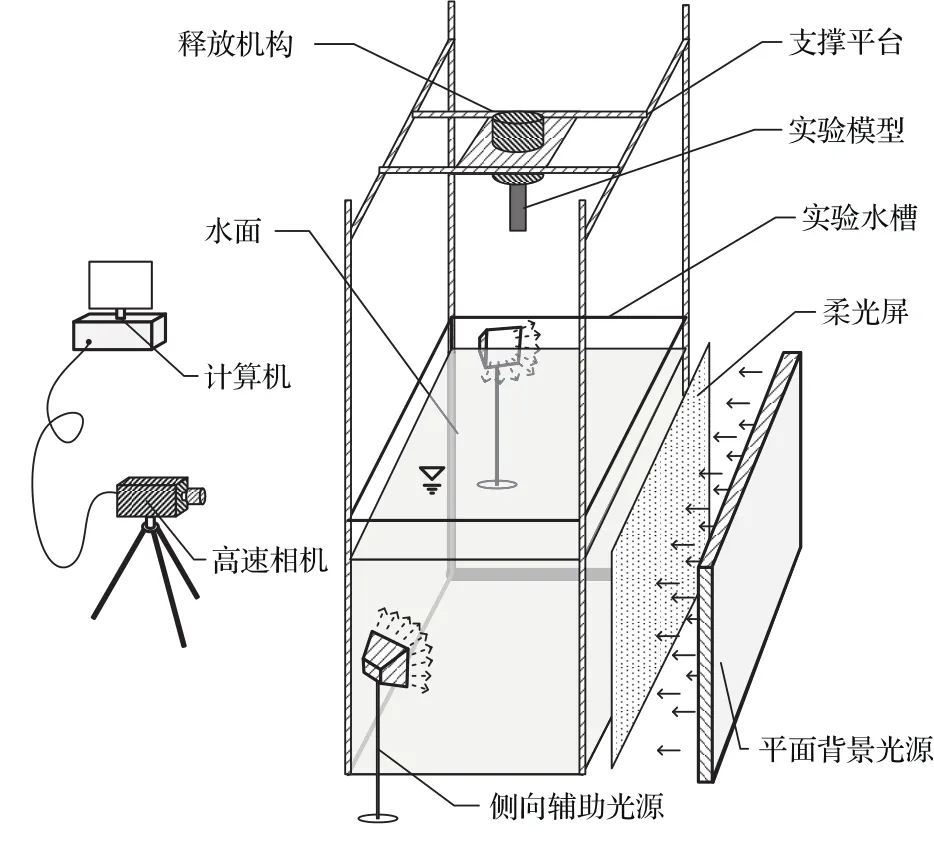
图1 试验系统示意图Fig.1.Experiment system of water-entry.

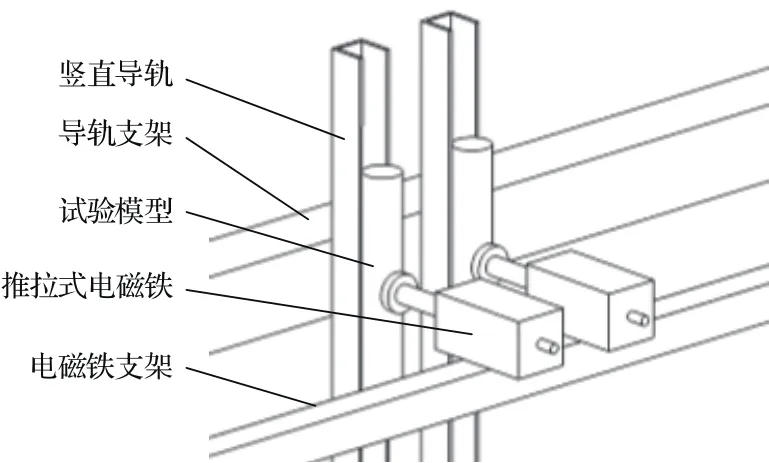
图2 释放机构示意图Fig.2.The mechanism to release the model.

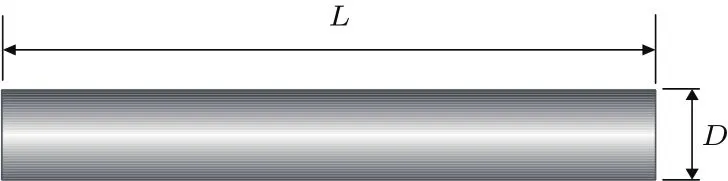
图3 模型尺寸Fig.3.Sketch of water-entry model.

2.2 实验结果分析

图4(a)给出了回转体单独入水空泡形态时历演化过程.回转体在入水过程中经历了入水撞击(t=0 ms)、开空泡(t=10—30 ms)、空泡闭合(t=10—50 ms)、空泡随动及空泡溃灭(t=60—80 ms)等五个阶段.在入水撞击阶段,回转体通过入水冲击将其自身动能传递给附近水流体,水流体形成向外排开运动,入水空泡形成;在开空泡阶段,回转体通过阻力作用不断将动能传递给附近水流体,致使回转体底面边缘处形成持续的流动分离,在宏观上表现为空泡敞开(t=10—30 ms);在空泡闭合阶段,气水界面处流体质点在运动过程中受到压力与表面张力的作用,做减速运动,当速度减小为0时开始反向加速,使得空泡形成“颈缩”现象,空泡发生闭合(t=40—50 ms);空泡完成闭合后,回转体底面仍不断形成流动分离,分离所形成的空腔需要空气进行填充,使得封闭在空泡内部的气体随着分离所形成的空腔位置的变化而流动,空泡形成随动(t=60—80 ms);在随动空泡形成后,闭合点处空泡内外存在压力梯度,使得水流体沿回转体壁面向泡内流动,形成回射流,空泡界面受回射流撞击而逐渐云化溃灭.

图4(b)给出了回转体同步并联入水空泡形态.对比单独入水空泡形态与并联入水空泡形态可以看出,单个回转体扰动下,流场流动具有轴对称性,因而空泡形态表现出良好的轴对称特征;在同步并联入水过程中,两空泡在回转体轴线内侧区域形成扰动,单空泡形态演化呈现出明显的不对称特征.在开空泡阶段,空泡向两回转体轴线中间区域的扩张受到了限制,以致两回转体外侧空泡半径明显大于内侧,中间区域形成的喷溅高度亦较外侧高;在空泡闭合阶段,两回转体轴线外侧区域空泡界面率先收缩,空泡闭合点偏向两回转体轴线内侧,且闭合时间变晚.在空泡随动阶段,随动空泡亦呈现出不对称特征.总之,在整个入水过程中,单独入水空泡始终保持很强的轴对称特性,而并联入水空泡则始终呈现较强的镜面对称特征.

图4 单独入水与并联入水空泡演化对比(V0=1.9 m/s) (a)单独入水空泡;(b)同步并联入水空泡Fig.4.Comparison of parallel water-entry cavities and single water-entry cavities:(a)Single water-entry cavities;(b)parallel water-entry cavities.

结合图5对空泡形态不对称原因解释如下:在开空泡阶段,外侧空泡自由扩张,而内侧空泡的发展受到了相邻圆柱体的影响.空泡在两圆柱体中间区域扩张时,空泡边界附近流体形成了对流,流体质点间动能传递受到限制而转变成流场势能,致使中间区域喷溅高度增加而空泡半径减小,空泡形态呈现出不对称特性.同时,由于中间区域较少的流体获得了来自两个圆柱体的动能,流动速度较外侧区域大,致使该区域流场压力低于外侧空泡界面附近的流场压力,导致在空泡闭合阶段,外侧空泡界面在较大压力作用下率先收缩,且收缩速率大于内侧空泡界面,最终使得闭合点偏向两圆柱体轴线内侧.

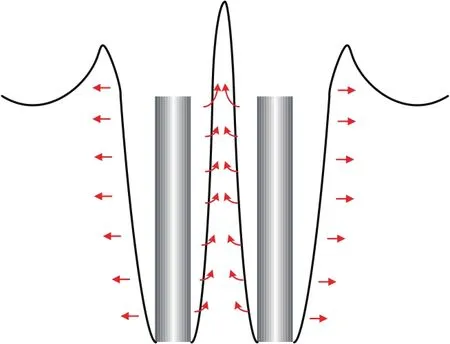
图5 并联入水空泡流动示意图Fig.5.The flow schematic of water entry cavity.

3 单独入水过程动力学方程

3.1 单独入水过程初边值分析

分析可知,在单独入水过程中入水空泡形态始终保持轴对称特性,因此空泡演化动力学模型建立在如图6所示的柱坐标系下.柱坐标原点取在回转体轴线与自由液面的交点处,r轴取回转体径向,z轴取回转体轴线,其正方向指向回转体运动方向.

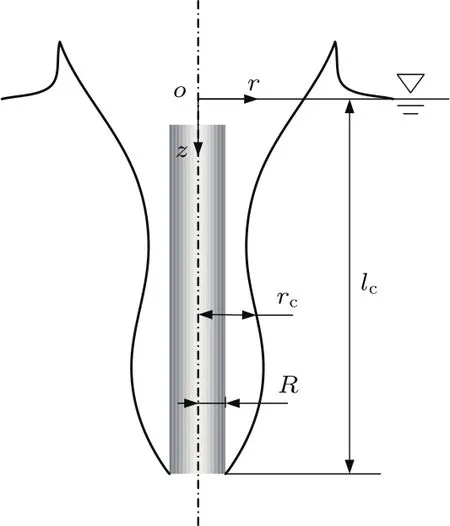
图6 回转体单独入水空泡示意图Fig.6.Schematic of single water-entry cavity.

对于单独回转体入水过程,可假设流体处于无旋状态.因此,流场的速度可以用速度势函数ϕ(r,z,t)进行描述,速度势ϕ(r,z,t)在流域内满足Laplace方程:

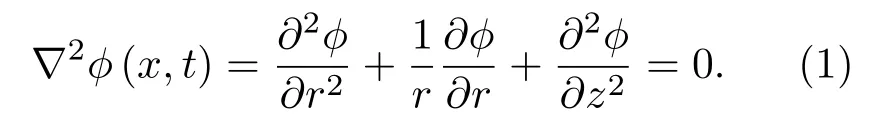
此时,流域内的速度分布可以用下式表示:

在自由液面处SF(r,t)处,速度势满足欧拉方程:

其中ps为自由液面处的压力,ρ为液体密度.在空泡闭合前,该压力恒等于大气压.在回转体表面,速度势满足物面条件:

式中,v为回转体运动速度,n=(nz,nr).速度势在远场满足远场边界条件:

在初始时刻,运动体仅仅触碰到了自由液面,此时,自由液面尚处于静止状态,初始速度势满足如下初始条件:

3.2 回转体动力学方程及空泡演化方程

在回转体过程中,其动力学方程可表达如下:

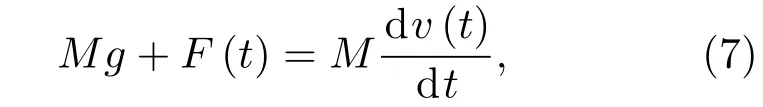
式中M为回转体质量,F(t)为回转体受到的流体动力.回转体在入水过程中,仅头部沾湿,因此流体动力可视为回转体头部所受到的流体压力.该流体压力由动压和静压两部分组成,其表达式为

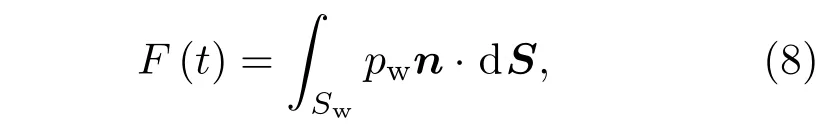
式中,pw为回转体头部沾湿面上受到的压力,其满足伯努利方程:

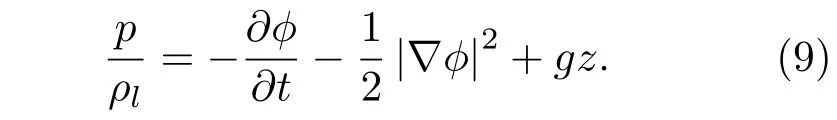
将(8)和(9)式代入(7)式得到回转体单独入水过程的动力学方程如下:

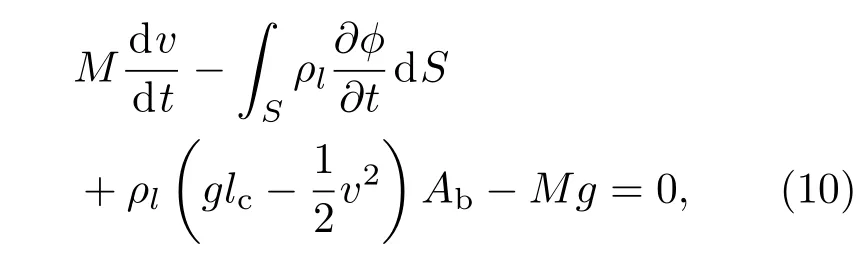
式中,Ab为回转体底部面积,Ab=πR2,R为底部圆形面半径;lc为空泡长度,其满足

对空泡进行细长体假设[20],即dr/lc=ε≪o(1),其中dr为空泡直径,此时,在空泡壁面附近的流动可以假设为二维流动:

此时,(1)式可简化为

对于空泡发展过程,在入水空泡初生时刻,其半径等于回转体半径.因此入水空泡半径演化的隐式方程:

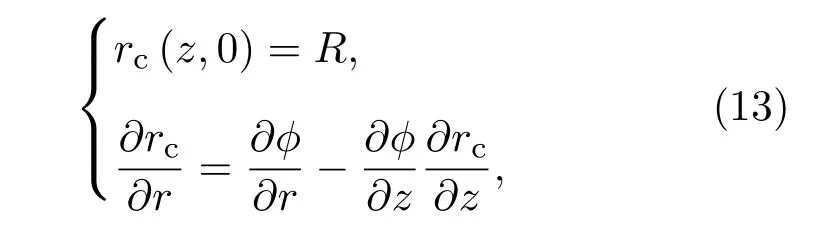
其中,rc为空泡直径.

3.3 速度势分析

基于建立的入水空泡半径演化方程(13)可知,若给出速度势ϕ(r,z,t),则可得到入水空泡半径的演化规律,因此本节基于渐进理论对速度势函数ϕ(r,z,t)进行分析.

为了描述空泡界面的运动,入水过程的速度势可以看作由一个位于回转体底面中心处的点源ϕb和一个位于空泡轴线处的线源ϕc组成:

空泡形成扩张的速度主要来源于回转体底部的空泡分离点.因此,空泡的扩张运动主要受三维点源ϕb的作用[14]:

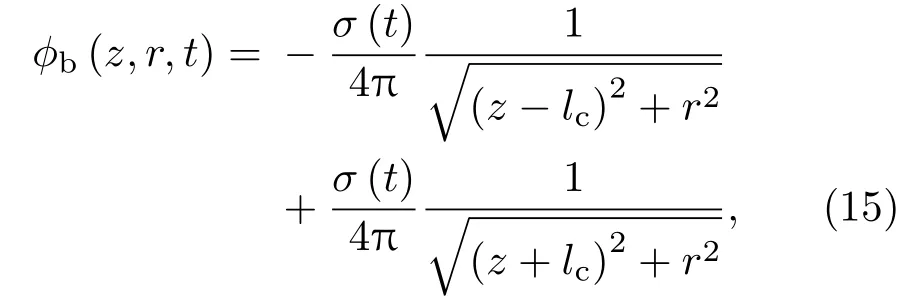
上式第二项对空泡演化的作用为抑制作用,由于对空泡进行了细长假设[20],则(16)式的第二项为一小量,因此可忽略.根据文献[14],点源强度由下式给出:

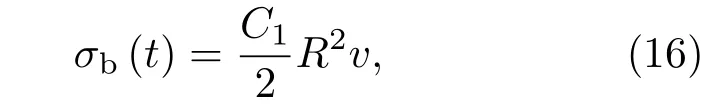
式中,C1为修正系数,文献中给出的C1=2.78,本文经过与试验结果对比,将其修正为2.76,得出点源速度势为

空泡的收缩主要受空泡轴线上分布的线源影响,其在某一空泡界面上具有二维作用效果,在整个空泡域,又具有三维作用效果.因此,空泡收缩的线源速度势可表示为

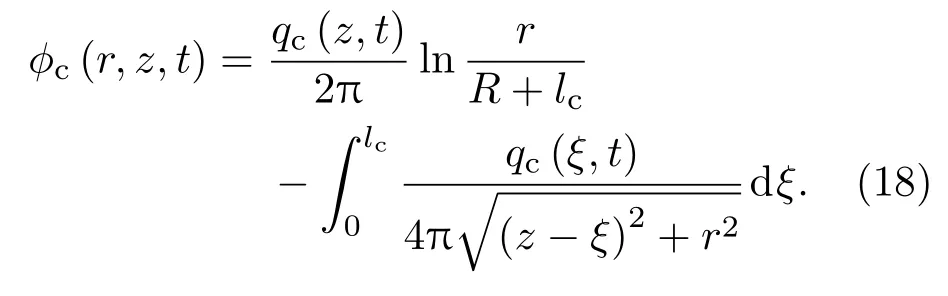
文献[14]中给出了线源的强度表达式,由此可以确定总速度势:

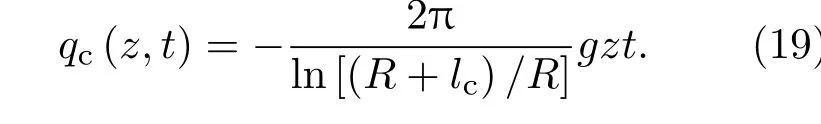
3.4 计算模型求解

将速度势代入(10)式得到回转体单独入水过程的完整动力学方程,并采用经典四阶龙格-库塔法对其进行数值求解.在求解过程中,时间步长取∆t=0.0001 s,在z方向(入水方向,如图2所示)的离散取∆z=0.001 m.图7给出了求解所得z方向位移随时间的变化与试验结果的对比,从图中可以看出,计算结果与试验结果符合良好.

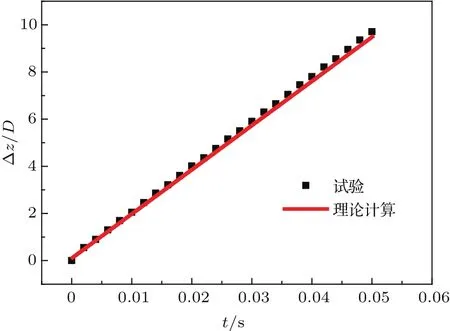
图7 位移结果对比(V0=1.9 m/s)Fig.7.Comparison of theory model calculative results and experimental results.

图8给出了入水空泡形态计算结果与试验结果的对比.从图中可以看出,整体上看计算结果与试验结果符合度较好,证明了该理论模型计算结果的正确性.在靠近自由液面处,计算模型结果较试验结果差别较大,这是由于计算模型中忽略了自由液面处的非线性喷溅流动,但并不影响入水空泡整体形态预测.

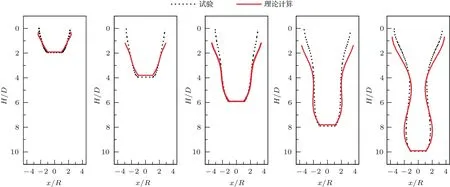
图8 入水空泡形态计算结果与试验结果对比(V0=1.9 m/s)Fig.8.Comparison of water-entry cavities of calculative and experimental results(V0=1.9 m/s).

4 同步并联入水过程双空泡演化扰动模型

4.1 动力学建模简化方法

在回转体同步并联入水过程中,回转体空泡外侧的发展呈自由扩张状态,内侧发展受到来自相邻空泡的干扰,而呈现出受迫演化状态.由第2节对并联入水空泡演化试验结果的分析,发现空泡在空间上呈对称特性,因此可将内侧区域空泡演化对称面作为扰动势对内侧空泡的发展演化进行分析.该扰动势的作用范围为∆,如图9所示.

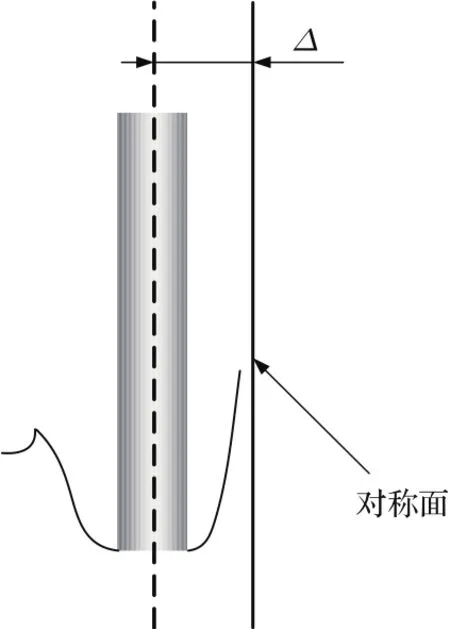
图9 对称面扰动势作用示意图Fig.9.Schematic of symmetry plane disturbance potential.

引入对称面处的扰动势,将入水空泡的演化通过二维轴对称的方法进行分析,其在三维空间中相当于引入了一个柱面约束,空泡在该柱面约束下进行轴对称受迫发展,如图10所示,该约束柱面可称为有势壁面.

图10 二维轴对称模型有势壁面约束本质示意图Fig.10.Schematic of potential wall constraint of the planar axisymmetrical model.

4.2 有势壁面速度势分析

由第2节体并联入水空泡演化特性分析可知,回转体入水过程约束势ϕs可认为由两部分组成,一部分是对扩张的约束,另一部分是对收缩的约束.结合3.3节关于速度势分析可知,空泡的扩张主要受位于回转体底部中心处的点源速度势ϕb的影响,而空泡的收缩主要受位于空泡轴线处的线源速度势ϕc作用.因此,对于空泡扩张与收缩的抑制,我们同样引入一个随回转体底部中心运动的点汇ϕb,s和位于空泡轴线处的线源ϕc,s.有势壁面的速度势则可以表示如下:

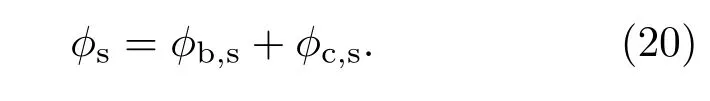
对于ϕb,s的分析,根据势流叠加原理,通过分析ϕb,s与ϕb的合速度势ϕb,sum来给出ϕb,s,ϕb,sum可由下式表示:

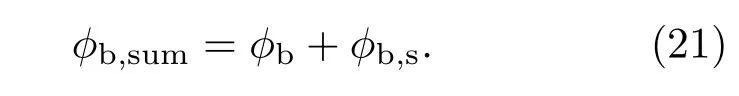
合速度势ϕb,sum可用三维点汇表示:

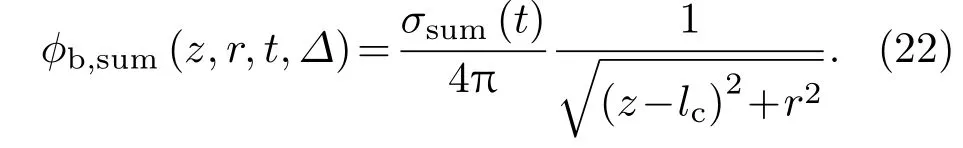
其点汇强度σsum(t)与扰动势无量纲作用范围˜∆(˜∆=∆/R)呈负相关,且根据试验结果,随着入水时间的增加,空泡最大直径减小,内外侧空泡直径差异减小,表明其对空泡扩展的约束与时间呈负相关.

根据有势壁面的不可穿越性,合速度势需要满足如下边界条件:

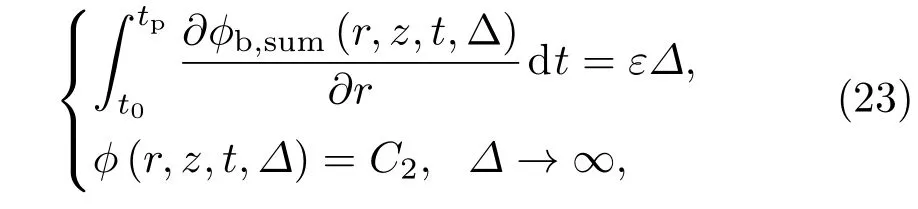
其中,tp为空泡的无量纲闭合时间,tp=Tv/R,T为空泡闭合时间,可按照文献[21]给出的经验公式求得:根据试验修正给出.(24)式给出了满足上述条件的点汇强度:

其中C1=2.76.

将(24)式代入(26)式得到合速度势为

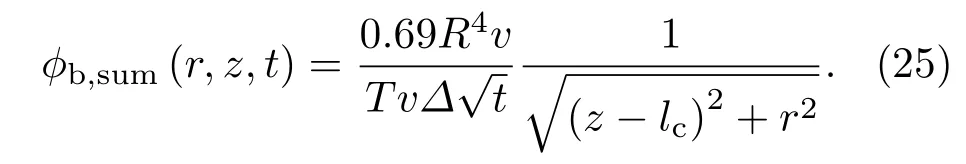
根据势流叠加原理推得有势壁面的点汇如下:

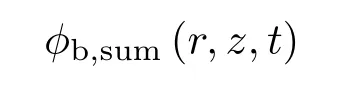
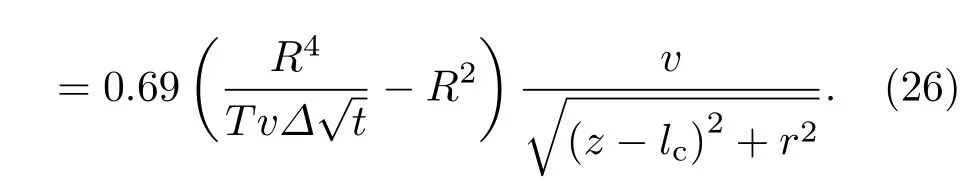
线源ϕc,s可以通过在r=2∆处引入一个相同强度的线源进行表示,其源强度由(19)式给出,得到ϕc,s如下:

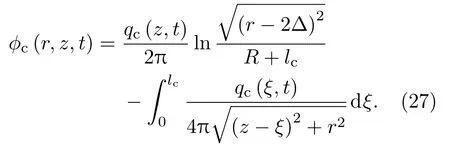
4.3 计算模型验证

速度势代入回转体动力学方程,采用经典四阶龙格-库塔法求解,得到在有势壁面影响下的位移,并将其与单独入水位移和试验结果进行比较,如图11所示.从图中可以看出,有势壁面对回转体z方向的位移影响很小.

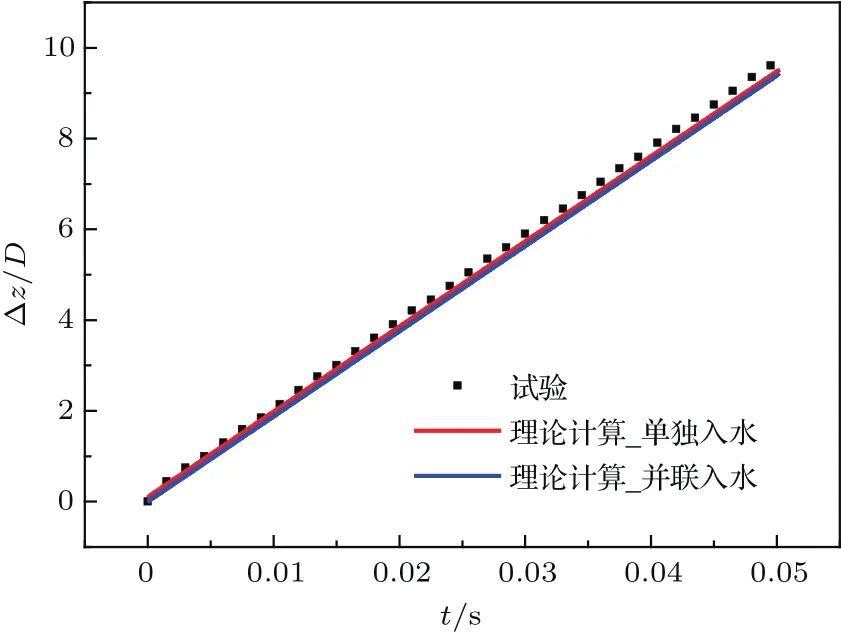
图11 位移结果对比(V0=1.9 m/s)Fig.11.Comparison of displacement results.

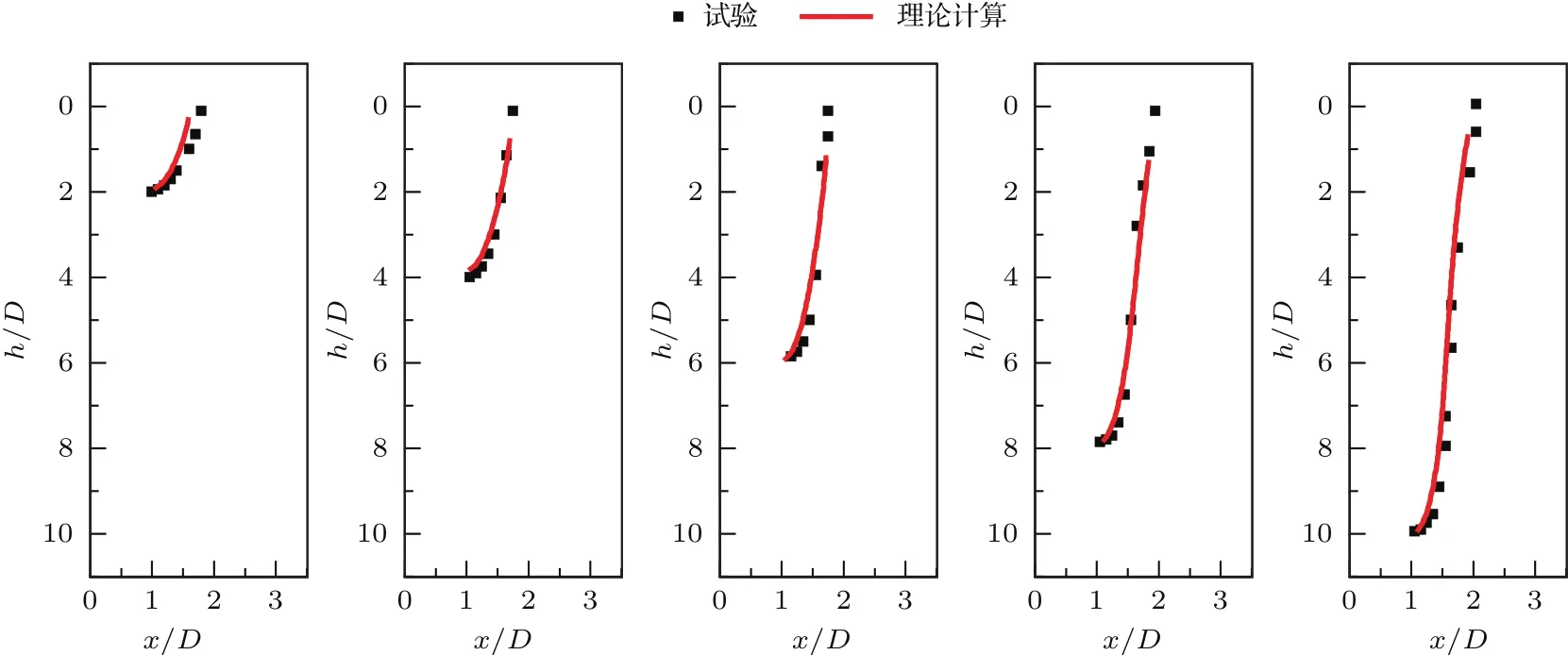
图12 计算结果与试验结果对比(V0=1.9 m/s)Fig.12.Comparison of water-entry cavities of calculative and experimental results.

基于第3.4节中对回转体位移的求解结果,开展在有势壁面约束下的空泡半径演化计算,在z方向的离散取∆z=0.001 m,图12给出了有势壁面约束下,空泡半径与试验工况下两回转体轴线内侧空泡半径的对比.从图中可以看出,理论结果与试验结果符合度较好,证明了该扰动模型的正确性.

5 三维空泡形态演化模型

5.1 非线性影响函数建立

由4.1节分析可知,在空泡的演化中,空泡沿回转体的径向扩张,对称面对空泡的影响区域如图13所示,白色区域空泡均呈现自由扩张,仅在灰色区域空泡会受到对称面的影响.

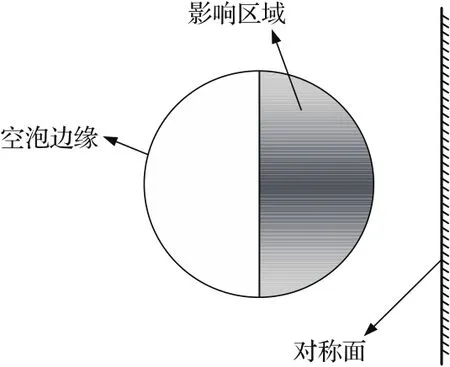
图13 对称面对空泡演化的影响区域Fig.13.Schematic of the influence region of symmetry plane on the cavity evolution.

基于上述的影响区域,我们将柱坐标系下的柱面有势壁面展开为笛卡尔直角坐标系下的有势平面,其对空泡的影响通过影响函数β来确定,其原理示意如图14所示.

设空泡的实际半径为rc,在有势壁面完全影响下的空泡半径为rc1,自由扩张半径为rc2,则其三者的关系可用下式表示:

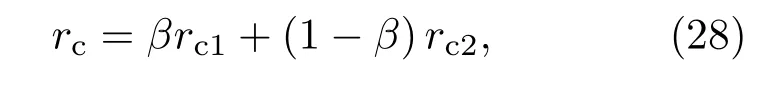
其中,β为影响函数,其具体形式如下文所述.

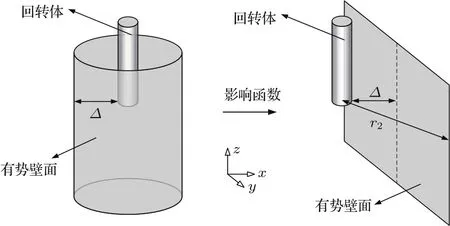
图14 有势壁面展开示意图Fig.14.Schematic of the potential wall expansion.

以有势壁面完全影响下的空泡边界与展开后的有势壁面之间的距离作为影响函数权重,在如图15所示的极坐标系下进行推导,其中l1为有势壁面,l2为有势壁面完全约束下的空泡半径,r1为回转体中心到圆柱有势壁面的距离,r2为回转体中心距离展开后的有势壁面的径向距离.

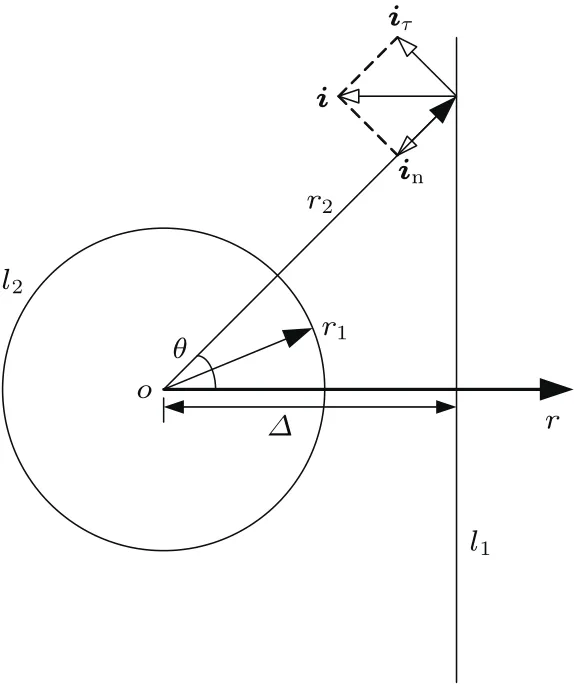
图15 极坐标系Fig.15.Polar coordinate system.

(29)和(30)式给出了l1和l2在极坐标系下的曲线方程:

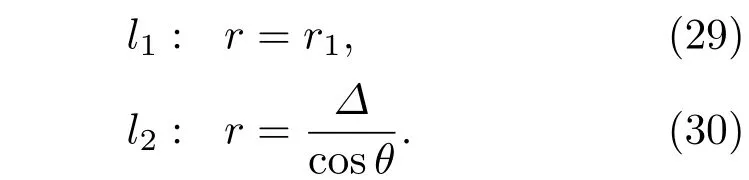
两条曲线间的距离如下:

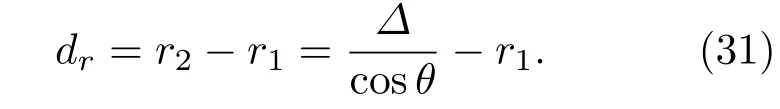
图15中,i为有势壁面的法向,对空泡壁面的影响其主要作用的分量为空泡边界的法向分量in,因此,影响函数的非线性假设如下:

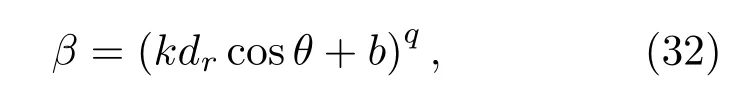
其中,k,b和q均为未知参数.

上式需要满足边界条件:

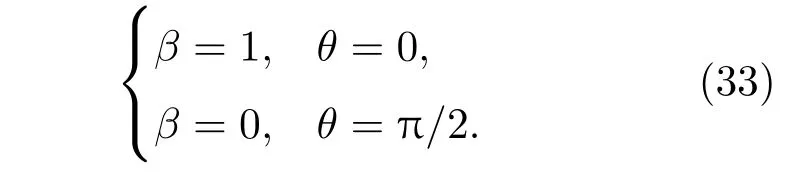
此外,在θ=π/2处,即未受影响区域和受影响区域交界处,空泡截面边界应满足连续可导条件.在笛卡尔坐标系下,取1/2空泡截面,未受影响区域,空泡截面为一1/4圆,其在x=0处∂y/∂x为0,因此受影响区域在该处也应满足:

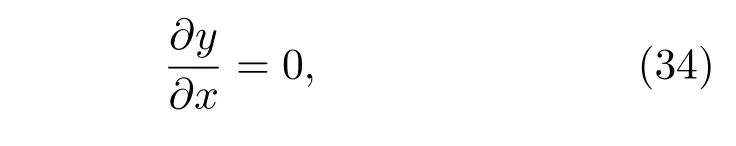
其中

得到影响函数β的表达式如下:

5.2 计算结果验证

基于5.1节中对影响函数的推导,对基于影响函数的三维空泡演化理论模型进行验证.图16给出了基于影响函数的空泡同步并联入水三维空泡形态计算结果及其与试验结果的对比.从图中可以看出,计算结果与试验结果符合较好,说明了该空泡演化模型的正确性.

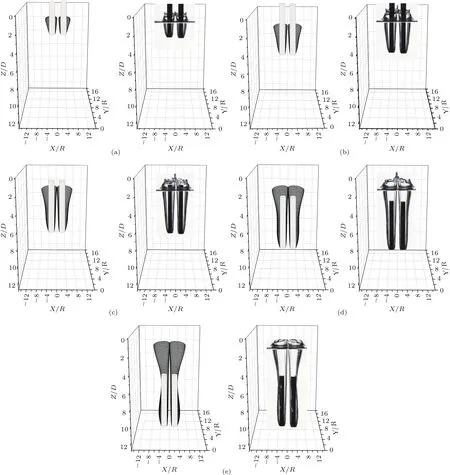
图16 三维空泡理论结果与试验结果对比 (a)t=0.01 s;(b)t=0.02 s;(c)t=0.03 s;(d)t=0.04 s;(e)t=0.05 sFig.16.Comparison of three-dimensional water-entry cavities of calculative and experimental results:(a)t=0.01 s;(b)t=0.02 s;(c)t=0.03 s;(d)t=0.04 s;(e)t=0.05 s.

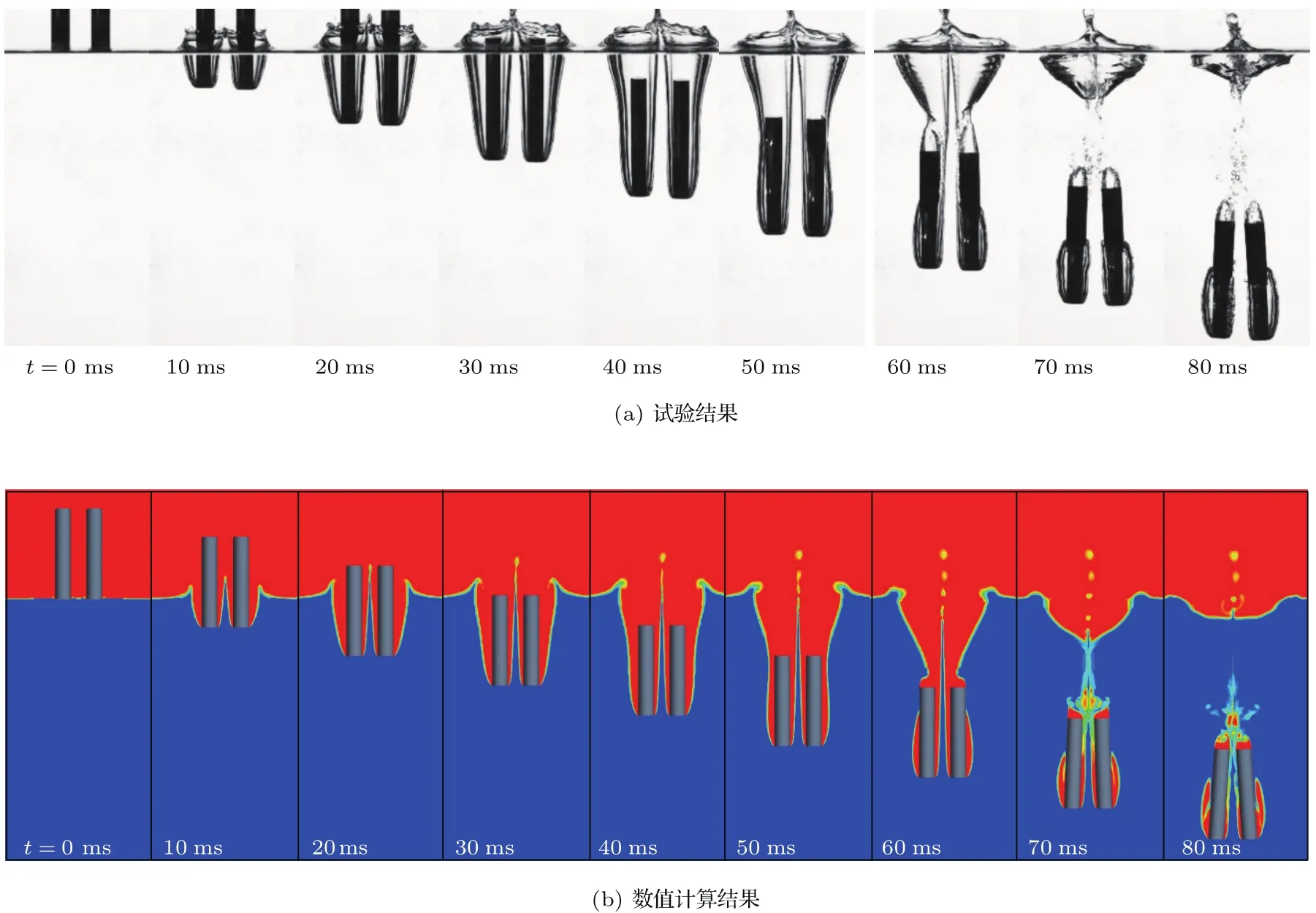
图17 并联入水空泡试验与数值计算对比(v0=1.9 m/s) (a)试验结果;(b)数值计算结果Fig.17.The water-entry cavity in paraller of experimental results and numerical results.

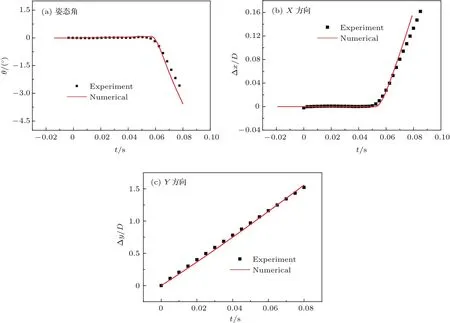
图18 并联入水位移特性数值计算结果与试验结果对比Fig.18.Comparison of the numerical results and experimental results.

由于试验过程中难以捕捉空泡横截面形状,因此我们采用数值模拟结果对三维空泡演化模型的正确性进行验证[22].为验证数值计算结果的有效性,图17给出了回转体以1.9 m/s速度并联入水过程中,入水空泡形态实验与数值计算结果的对比.图18分别给出了回转体并联入水过程空泡形态时历演化与角位移、线位移时历曲线的对比.从图中可以看出,数值计算所得的空泡形态在两弹轴线内侧区域的发展程度较试验结果略大,但空泡形态轮廓的整体演化与试验符合度较好.位移特性曲线与试验结果符合较好.综上分析,可认为本文数值方法适用于回转体并联入水过程的研究.

图19给出了t=0.05 s时,四个不同深度处空泡界面理论值与数值仿真结果的对比.从图中可以看出,计算结果与数值结果具有较高的符合度,表明引入影响函数后的三维空泡演化计算模型的正确性,基于该模型可较为准确地预测空泡在三维空间的演化过程.

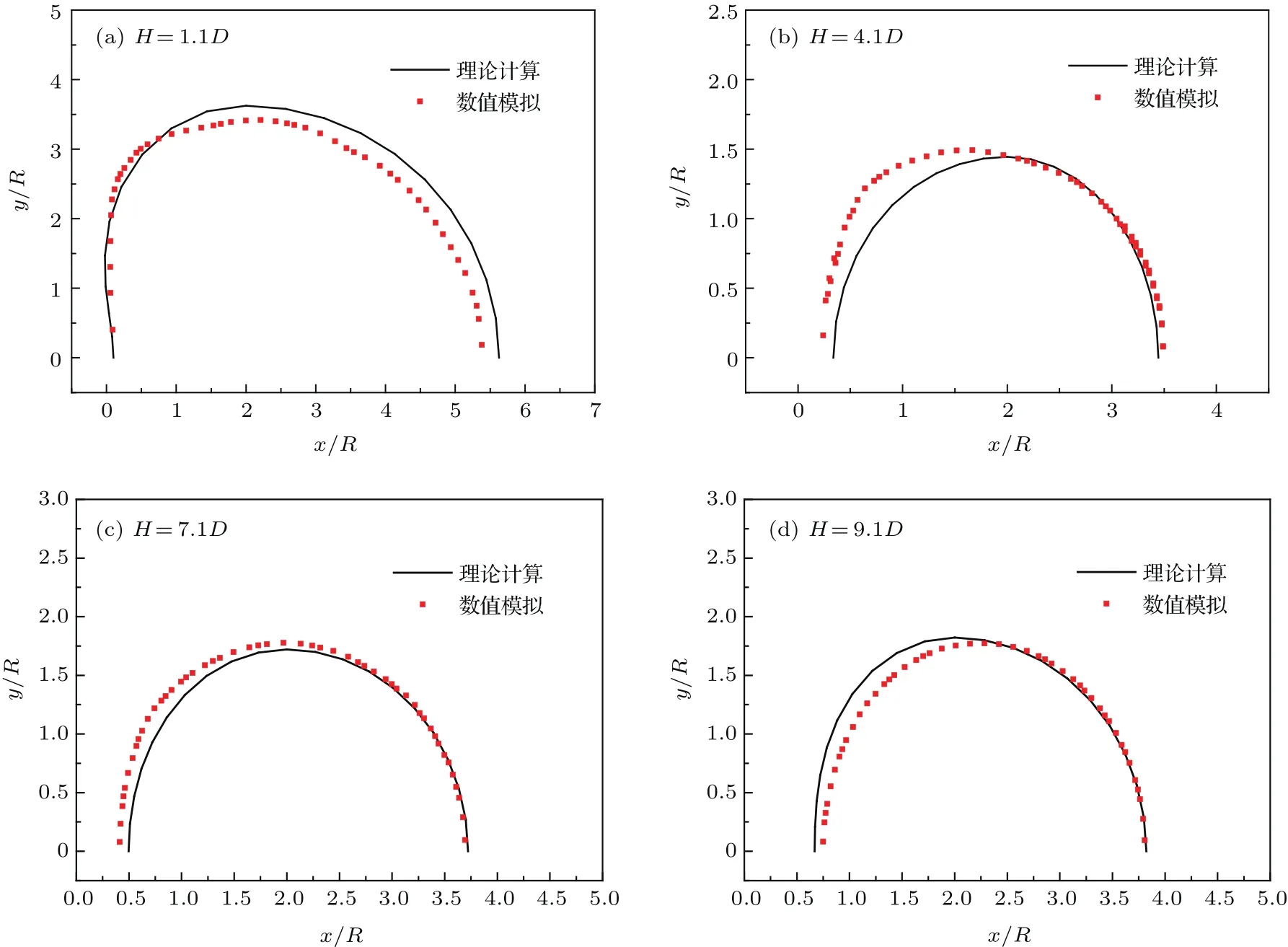
图19 空泡截面形状理论结果与数值结果对比(t=0.05 s)Fig.19.Comparison of the cavity cross-section of calculative and experimental results.

6 并联入水空泡三维形态演化特性研究

不同于单独入水过程的轴对称空泡,并联入水空泡半径沿回转体轴线呈非均一分布,且在空泡的不同发展阶段,空泡随周向的变化亦呈现出不同的变化规律.图20给出了极坐标系下t=0.05 s时,不同深度处空泡半径随极角(范围取0—π)的变化规律,此时空泡已在回转体表面形成闭合,图20(a)给出了闭合点上方空泡半径随极角的变化,图20(b)给出了闭合点下方空泡半径随极角的变化.从图中可以看出,在闭合点上方,随着入水深度的增加,空泡半径随极角的变化呈现出从正相关到负相关的变化;在闭合点下方,随着深度的增加,空泡半径呈现出从负相关到正相关的变化.该现象的产生主要是受空泡颈缩的影响,在闭合点上方,随着入水深度增加,空泡截面逐渐靠近闭合点,此时,自由演化区空泡(θ=π/2—π)随着入水深度增加,收缩量增大;抑制演化区,有势壁面对空泡的收缩亦存在抑制作用,空泡收缩速率低于自由演化区,使得在闭合点附近,抑制演化区的空泡半径大于自由演化区,进而形成了随着入水深度的增加,空泡半径随极角的变化呈现出从正相关到负相关变化的现象.在闭合点下方,靠近闭合点处,即H=6.1D处,空泡截面处在收缩过程中,其半径随极角的变化呈负相关的原因同上;随着深度的增大,空泡截面的运动从收缩过渡至扩张,在该过程中,抑制演化区受有势壁面影响,扩张受限,使得自由演化区空泡半径大于抑制演化区,因而空泡半径随极角变化呈现出正相关特性.

从图20中还可以发现,在闭合点上方,无论是自由演化区还是抑制演化区,空泡半径随入水深度的增大呈单调减小趋势;在闭合点下方,抑制演化区空泡半径随入水深度的增大单调减小,而自由演化区空泡半径随深度增加呈先增大后减小的趋势.该现象与空泡截面的发展程度有关,在闭合点上方,各空泡截面均已充分发展并进入收缩阶段,因此空泡半径随入水深度具有较好的单调性;而在闭合点下方,自由演化区尚有未完全发展的空泡截面,因而出现了空泡半径先增大后减小的趋势.

为分析有势壁面对并联入水空泡半径影响的空间变化规律,定义并联入水空泡加权半径如下:

其中,r为并联入水空泡半径,rc2为未受有势壁面影响的单独入水空泡半径.

图21给出了空泡加权半径随极角的变化规律,同样,图21(a)曲线给出了闭合点上方不同深度处的半径变化,图21(b)曲线给出了闭合点下方不同深度处的半径变化.从图21(a)中可以看出,在闭合点上方,随着入水深度的增加,抑制演化区空泡半径与自由演化区空泡半径的比值逐渐增大,出现该现象的主要原因在于抑制演化区的空泡收缩率远小于自由演化区.而对于闭合点下方,图21(b)中可以看出随着入水深度的增大,抑制演化区空泡半径与自由演化区空泡半径的比值随深度增加先减小后增大,且当深度较大时,其值非常接近.

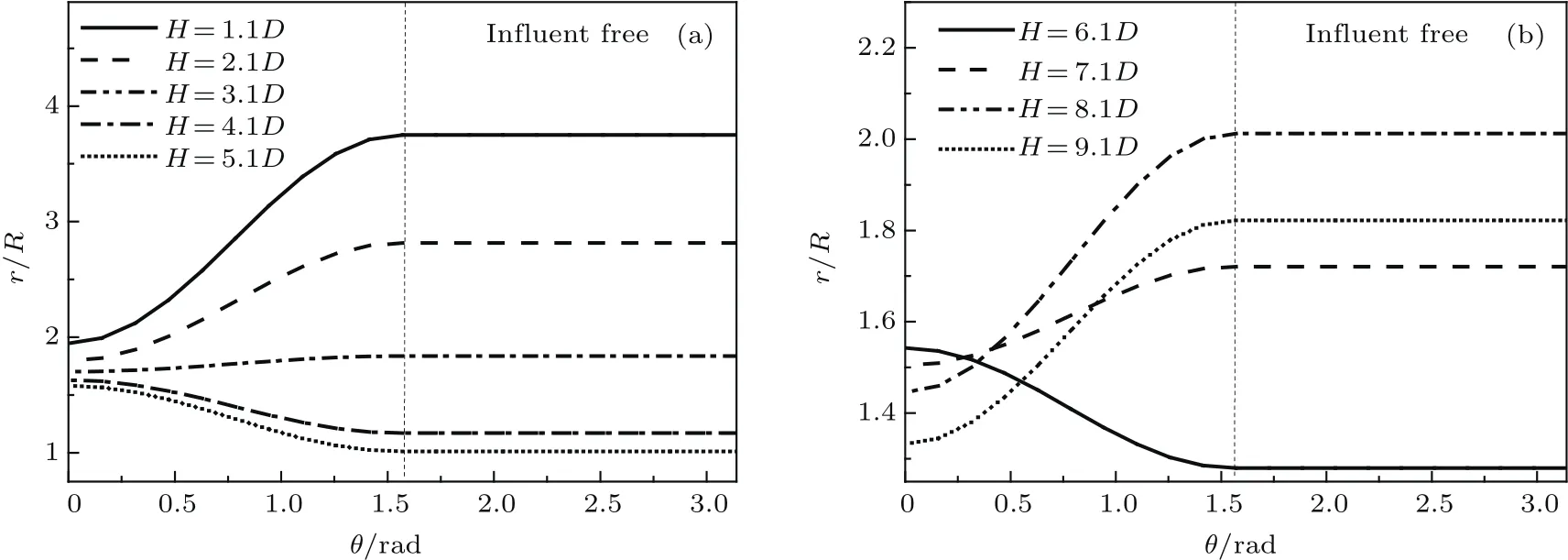
图20 空泡半径沿周向变化规律(t=0.05 s) (a)闭合点上方;(b)闭合点下方Fig.20.The cavity radius of circumferential direction.

图21 抑制演化区空泡加权半径沿周向变化规律(t=0.05 s) (a)闭合点上方;(b)闭合点下方Fig.21.The of the suppressed region.

图22给出了t=0.05 s时不同深度处空泡截面形态,其中图22(a)为闭合点上方不同深度空泡截面形态,图22(b)为闭合点下方不同深度空泡截面形态.在闭合点上方,空泡经历了较为充分的演化,使得空泡有了明显的扩张、收缩运动,随着深度增大,空泡截面逐渐缩小.在H=1.1D处,空泡截面形成了过度演化,即空泡截面边界在x方向超越了空泡的理论x最大值——空泡对称线处的空泡形态x值.分析其形成原因,在该深度处,收缩势较弱,空泡扩张程度较大,然而随着极角的增大,有势壁面对扩张的抑制逐渐减弱,在该位置处,空泡的扩张程度与抑制程度的比值超过了对称线处空泡扩张程度与抑制程度的比值,使得空泡形成过度演化.空泡的过度演化只形成于深度较浅的位置,在深度较深的位置,空泡扩张程度总体较弱的地方难以形成过度演化,如图22(b)所示.

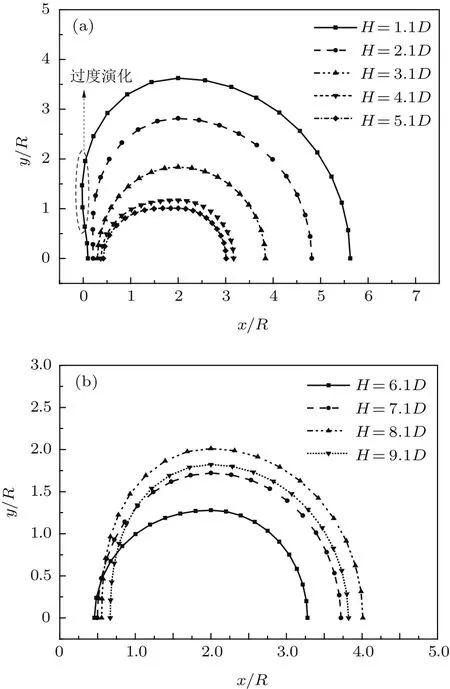
图22 不同深度处空泡截面形态(t=0.05 s) (a)闭合点上方;(b)闭合点下方Fig.22.The cross section shape of various depth.

图23分别给出了H=1.3D,H=3.3D,H=5.3D三个深度处极坐标系下不同时刻的空泡形态.从图中可以看出,随着时间的增加,极坐标系下的空泡半径呈先增大后减小的趋势,且增大速率随着极角的增大而增大.该过程反映了空泡界面的经典演化特性.在空泡发生收缩时,由于影响函数在极角越大处产生的收缩抑制越小,使得极角较大的位置率先发生收缩,而此时极角为0处的空泡尚未形成收缩.随着深度增大,极角较大位置的空泡收缩速率越快.

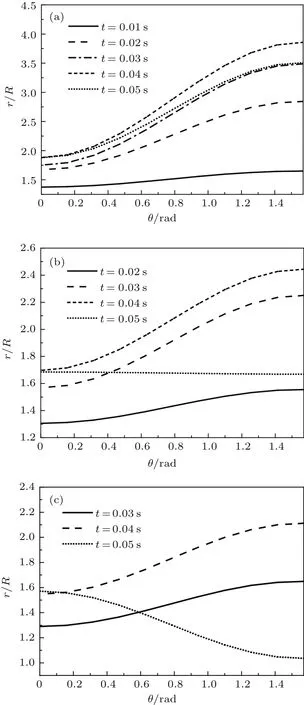
图23 极坐标系下空泡截面半径时历演化 (a)H=1.3D;(b)H=3.3D;(c)H=5.3DFig.23.Time evolution of cavity cross section shape in polar coordinate system:(a)H=1.3D;(b)H=3.3D;(c)H=5.3D.

图24给出了极坐标系下不同时刻的空泡加权半径随极角的变化规律.从图中可以看出,空泡加权半径与空泡截面半径随时间的变化规律基本一致.此外,从图中还可以看出,在空泡从扩张向收缩过渡的过程中,空泡加权半径逐渐靠近,在H=3.3D处,t=0.03 s与t=0.04 s的加权半径已接近完全重合.

图25给出了笛卡尔坐标系下的空泡形态时历演化,从图25(a)中可以发现,在空泡形成之初,空泡尚未出现过度演化现象,随着时间的推移,空泡过度演化逐渐产生,其程度也逐渐增大,在空泡的收缩过程中,过度演化逐渐得到缓和.而随着深度的增大,在空泡演化的整个过程中,均没有过度演化现象产生.

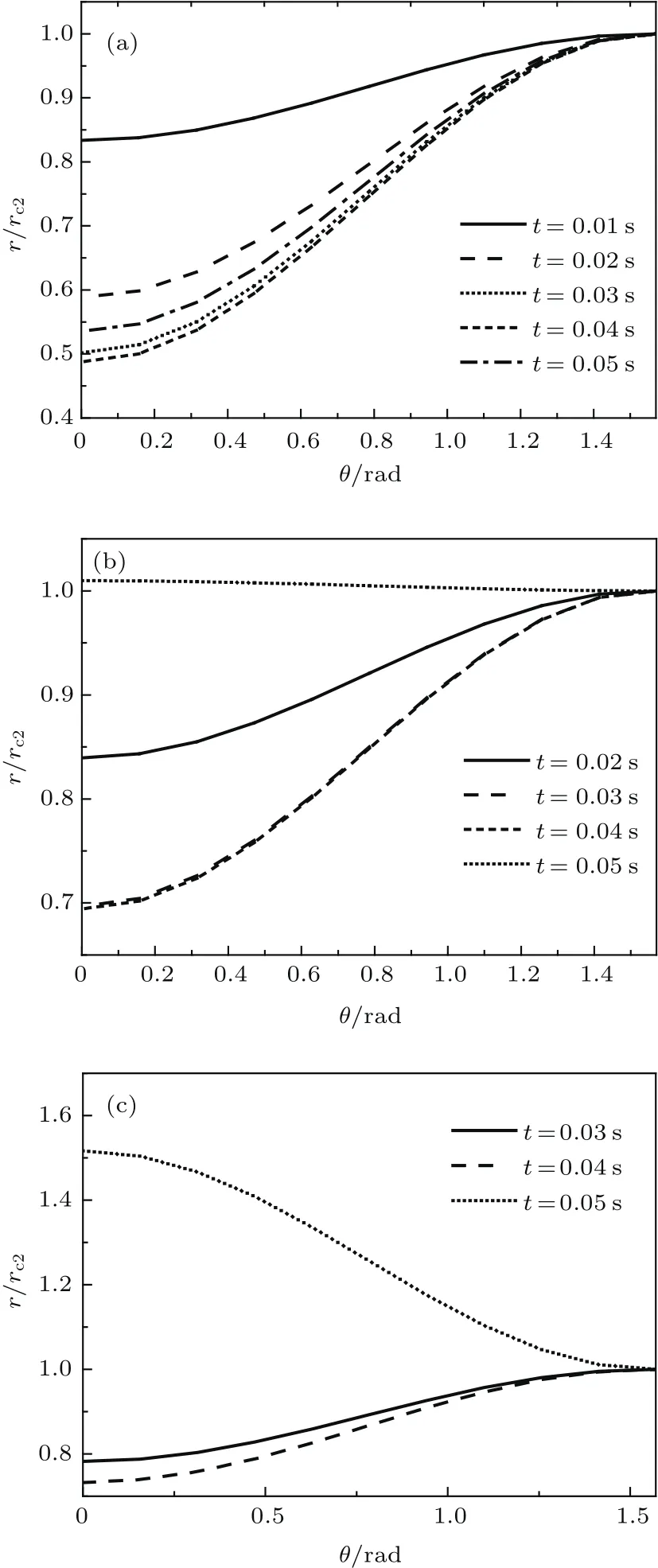
图24 极坐标系下空泡加权半径时历演化 (a)H=1.3D;(b)H=3.3D;(c)H=5.3DFig.24.Time evolution of in polar coordinate system:(a)H=1.3D;(b)H=3.3D;(c)H=5.3D.

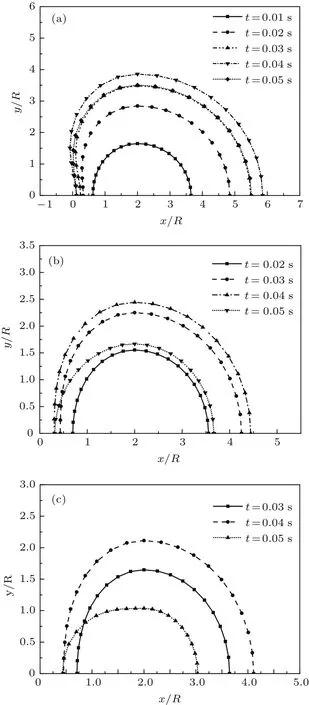
图25 笛卡尔坐标系下空泡截面形态时历演化 (a)H=1.3D;(b)H=3.3D;(c)H=5.3D.Fig.25.Time evolution of in Cartesian coordinate system:(a)H=1.3D;(b)H=3.3D;(c)H=5.3D.

7 结 论

本文基于势流理论,通过二维轴对称方法分析了回转体单独入水过程空泡动力学模型.基于回转体单独入水空泡的动力学模型,引入有势壁面和影响函数,建立有势壁面影响下的空泡受迫演化模型,并基于该模型分析了并联入水空泡三维演化特性,得到如下结论.

1)回转体入水过程流场速度势可以看作由一个随回转体运动的点源和位于空泡轴线处的线源叠加产生,其中空泡的扩张运动主要受点源的影响,而收缩运动主要受线源影响.

2)在并联入水过程中,双空泡演化在空间呈镜面对称,空泡间的相互扰动可以通过引入有势壁面进行分析.有势壁面对空泡的演化呈抑制作用,该抑制作用包含两个方面,分别为对扩张的抑制和对收缩的抑制.

3)并联入水空泡半径随极角的变化与空泡截面所处深度有关,在靠近闭合点附近的抑制演化区空泡截面半径随极角的增大而逐渐减小,远离闭合点处的抑制演化区空泡截面半径随极角的增大而增大,空泡与半径规律相反.

4)在深度较浅处,空泡扩张过程中会形成过度演化,空泡收缩阶段过度演化逐渐被削弱并消失.