光线庞加莱球法构建的结构光场及其传输特性研究∗

张书赫 邵梦 周金华

(安徽医科大学生物医学工程系,合肥 230032)

(2018年5月8日收到;2018年9月29日收到修改稿)

1 引 言

随着激光技术的发展与波前调制技术的进步,越来越多具有新奇性质的光场呈现在人们眼前.例如厄米-高斯光束,它的横截面光斑分布为矩形矩阵状;拉盖尔-高斯光束携带轨道角动量,强聚焦后能使被俘获物体产生规则的旋转[1];无衍射光束[2]的光斑强度与大小在较长的传输范围内保持不变;自加速光束[3,4]的主瓣光斑在均匀介质中沿着曲线传播.在这些新奇的光束中,结构光束(包括最经典的三类结构光束为厄米-高斯光束、拉盖尔-高斯光束以及Ince-高斯光束[5,6])由于具有复杂的相位信息与光强分布被广泛应用于信息传递[7]、显微成像[8,9]或微粒操纵[10−12]等领域,促进了相应领域技术的发展.

在不同坐标系下赫姆霍兹波动方程在一定的边界和近似条件[6](如傍轴近似,缓变近似等)的特解[13],对应为结构光束.从设计激光器的角度分析,对于某一光学谐振腔而言,选取解方程的坐标系即选择光学谐振腔镜面的几何形状[14],赫姆霍兹方程相对应的解就为该光学谐振腔能稳定生成的光束.例如矩形曲面反射镜的谐振腔能获得厄米-高斯光束及其高阶模式,而在圆形曲面反射镜下能获得拉盖尔-高斯光束及其高阶模式[15].

从几何光学的角度来分析,光线在谐振腔的两个镜面之间稳定的往复反射,可以等效为某质点在曲面反弹板之间的往返反弹.若将质点在两个反弹板的往复运动向中间平面进行投影,其投影点的运动呈现为二维的简谐振动,而这个运动轨迹的形状为椭圆[16].考虑到庞加莱球面上的点可以描述单位圆内的椭圆,2017年Alonso和Dennis[16]提出了光线庞加莱球法设计复杂结构光束的一般方法.该方法可再现厄米-高斯光束与拉盖尔-高斯光束,并给出这些光束的光线表征与光场沿光线的传输方式[17]以及设计一些其他的结构光束.光线庞加莱球法给研究结构光束的设计与传输提供了新颖的、可视化的方案.

本文运用光线庞加莱球法结合梅花曲线设计了一系列结构光束,并展示了这些光束在束腰面的光场复振幅分布以及该类光束在一定条件下退化为拉盖尔-高斯光束以及局部无衍射光束[16](因为真正的无衍射光束,例如贝塞尔光束、马蒂厄光束和Airy光束等,都具有无限的能量,以保证光强在传播无限远的距离内都不发散.而文中的光束光强分布均被限制在光束的外焦散线内,只能在一定的传播范围内保证无衍射的特性,故称为局部无衍射光束).最后本文采用角谱衍射[18]展示这些结构光束在真空中的传输特性,包括光束的自修复特性以及无衍射特性,并采用光线追迹对这些性质予以解释.

2 光线庞加莱球法构建梅花形结构光束

2.1 庞加莱球与椭圆光线轨道

如图1所示,庞加莱单位球面上任意一点由经度角φ与纬度角θ共同确定.不同于以往庞加莱球描述偏振态的关系,这里仅取其球面上点的方位角与琼斯向量v的关系为[16]

每一个琼斯向量v可确定唯一一个实空间内斜椭圆的参数方程Q(τ)=(Qx,Qy)以及从Q点出发的光线的横向方向向量(x和y方向)P(τ)=(Px,Py),即

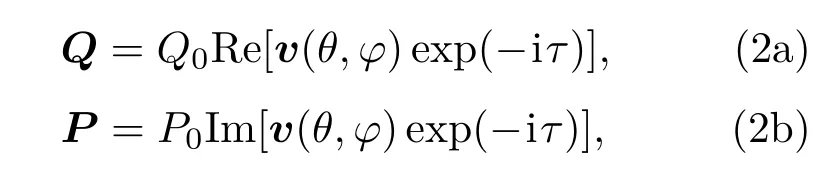
其中0 6 τ 6 2π;Q0为非负实数,决定了光束束腰宽度,其值越大光束束腰越宽;P0为非负实数,决定了光线偏离z轴的程度,其值越大光线偏离z轴角度越大.光线从椭圆上以Q(τ)为起点,以方向[P(τ),1]传播(在傍轴条件下有|P(τ)|≪ 1).这样均匀介质下光线方程(ray equation)就可以写为Q+zP.将这些光线方程结合文献[17]中光线构建光场的理论,能构建光束在三维空间中的光场分布.虽然该方法直接计算三维光场分布较为复杂,但是它经过简化后可以推导出光束在束腰平面内的光场分布公式(见第2.3节(9)式),并且光束在真空中传输后的光场可以通过衍射理论计算得到,故本文采用光线庞加莱球法计算光束束腰面的光场分布,并结合角谱衍射理论计算光束的三维光场分布.

理论上庞加莱球面的任意一组曲线都可以用来构建对应的光场,而直接分析三维曲线较为复杂.为了简化分析,我们只考虑位于庞加莱球上半球面的曲线.将该曲线投影到z=0平面(赤道平面),这样庞加莱球面的曲线与其赤道平面的投影曲线成为唯一的对应关系——在z=0平面上有且仅有一条曲线与庞加莱球面上已知曲线形状对应.研究庞加莱球面上三维曲线的问题从而简化为研究赤道平面的单位圆(Poincaré equatorial disk,PED)内二维曲线问题.

图1 庞加莱球面上点与实空间中椭圆的对应关系 (a)庞加莱球面上的点由经度角φ与纬度角θ共同确定;(b)实空间内椭圆的参数,可通过(1)式与(2a)式由庞加莱球面上的点来确定(参考视频mov1.avi)Fig.1.Relationship between an Ellipse in real space and a point on the Poincaré sphere:(a)The location of a point on Poincaré sphere is determined by longitude φ and latitude θ;(b)the parameter of an ellipse in real space can be described by a point on Poincaré sphere given by Eq.(1)and Eq.(2a)(see also mov1.avi).

2.2 梅花曲线作为PED路径

选取梅花曲线作为庞加莱球面空间曲线在PED内的投影路径,单位圆内的梅花曲线可以由心形线改写而来[19],其参数方程为

参数0 6 η 6 2π;非负整数b为花瓣数;无量纲参数a控制梅花填充PED单位圆的程度,a越大,曲线越趋向于单位圆.图2(a)展示了PED单位圆内a=b=3的三瓣梅花曲线,该曲线为图2(b)中庞加莱球面上空间曲线在PED上的投影.根据几何关系,庞加莱球面点的经度角φ与纬度角θ表示为η的参数方程,即

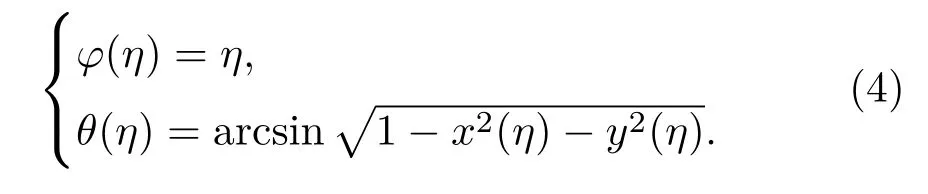
值得注意的是,并非所有由(3)式描述的梅花形PED路径都能适于构建光场.为了构建合理的结构光场,参数Q0和P0需要满足第一个量子化条件[16]

其中N为非负整数;k=2π/λ为光波数,λ为光波长.该量子化条件限制Q0和P0只能选取为分立值.以基模高斯光束束腰半径ω0为参考,Q0可表示为

王某某在网上看到快递已被程瀚签收后，便打电话过去要钱，谁知被程瀚态度强硬地拒绝。坐过牢的李某某觉得情况不对劲，便让王某某赶紧丢掉手机，自己也逃往千里之外的内蒙古鄂尔多斯。

图2 PED路径与庞加莱球面上三维曲线的关系 (a)PED内的投影为梅花曲线;(b)庞加莱球面曲线,该曲线所包络的庞加莱球面上的曲面面积为Ω,它在PED内的投影即是(a)中的PED路径Fig.2.Relationship between Plum blossom PED path and a spatial curve on the Poincaré sphere:(a)A plumblossom curve PED path;(b)a space curve(colorful)lays on the Poincaré sphere,the area of sphere surface within the colorful curve is Ω.The PED path in Fig.2(a)is the projection of the colorful space curve on Poincaré sphere.

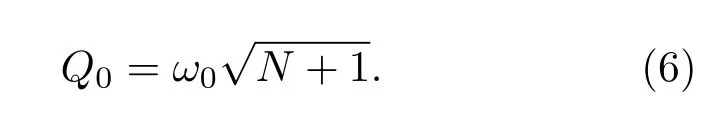
根据(6)式和光束束腰半径ω0就可得到Q0的值,进一步通过(5)式获得P0的值.此外,庞加莱球面上三维曲线所包围的球面部分的曲面面积Ω为关于a和b的函数.则第二个量子化条件为[16]

由于(2)式确定的椭圆尺寸依赖于Q0的大小,为了统一表示,这里令Q0=Q/Q0将坐标系归一化,使椭圆均被归一化到同一单位圆内,这个单位圆也被称为物理盘(physical disk).至此,PED上每一个点对应于庞加莱球上半球面上唯一的点,并对应于物理盘上唯一的一个椭圆.

如图3所示,图3(a1)中PED内一条三瓣梅花曲线c,过曲线c上每一点可找到与c外切且与单位圆内切的圆(图3(a1)中青色小圆),记这些圆的圆心为t1;此外还能找到与c内切且与单位圆内切的圆(图3(a1)中粉色小圆),记这些圆的圆心为t2.t1与t2的坐标可以通过数值求解的方法获得,根据中轴线的定义可知t1与t2即为PED曲线与单位圆的中轴线[20].图3(a2)为完整相切曲线.在物理盘上,根据坐标变换

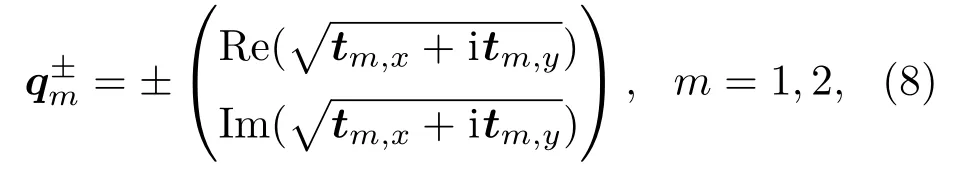
可以将PED内t1与t2的点分别映射到物理盘内的q1与q2,如图3(b1)所示(为清晰展示,图3(b1)仅绘出q1与q2曲线中一部分,完整的曲线见图3(b2)).q1与q2构成了归一化尺寸椭圆Q0=Q/Q0的外包络与内包络,乘以系数Q0后,就构成了实空间光束束腰面的焦散线,见图3(b2).外焦散线(蓝色曲线)决定了光束光斑图样的包络(例如厄米-高斯光束的矩形光斑阵对应了矩形外焦散线),内焦散线(洋红色曲线)决定了光束内部光斑较亮区域的位置.此外,拥有内焦散线的光束还具有一定的自修复特性[21].

图3 PED内曲线每个点构成物理盘内的椭圆(a1)PED内梅花曲线路径以及两中轴线t1与t2的一部分;(b1)物理盘上的椭圆以及q1和q2的曲线一部分;(a2)完整的t1(深蓝色)与t2(洋红色)曲线;(b2)完整的q1与q2曲线,他们分别构成椭圆的外与内包络线,对应于光束的外与内焦散线(参考视频mov2.avi)Fig.3.Each point in PED path corresponds to an ellipse in physical disk:(a1)Plum blossom PED path and parts of medial axes t1and t2;(b1)ellipses in physical disk and parts of q1and q2curves;(a2)full path of t1(deep blue)and t2(magenta);(b2)full path of q1and q2,q1and q2are ellipses’envelope curves,q1is the outer curve and q2is inner curve.They represent outer caustic and inner caustic of beam,respectively(See also mov2.avi).

当选取满足(5)和(7)式两个量子化条件的参数Q0,P0,a和b后,便可确定t1与t2或q1与q2的路径.

2.3 束腰面上光场计算

结构光束的束腰面上光场复振幅分布可由(9)式确定[16],

(11)式中上标T表示向量转置.此外(9)式中UN代表每个椭圆的光场贡献,其计算式为

其中HN为N阶厄米多项式.

(9)式的物理意义可以理解为“束腰面上的光场视作每个椭圆轨道的光场乘以对应的相位延迟后的干涉叠加”[16].对于满足第二个量子化条件(7)式的不同的曲线参数a和b,当选取合适的参数Q0和P0后就可以得到一个对应的结构光束束腰面光场分布.从(4)—(9)式可以发现,参数Q0与P0只影响光束的束腰大小与光线方向,而梅花曲线参数a与b决定了光场分布图样.当花瓣数b预先确定后,只需要计算满足(7)式的参数a,即计算整个束腰面上的光场分布.本文将展示b=0与b=1两个特殊花瓣数下的结构光场以及一个花瓣数为b=5情况下的结构光场.

3 梅花结构光束的传输特性

在下列计算中均选取N=45,n=15,λ=1.064µm和ω0=10µm(Q0≈ 67.82µm)的光束参数.光束瑞利距离zR=πω20/λ≈295.26µm.

3.1 b=0的结构光束

当b=0时梅花曲线(3)式退化为半径等于[a/(1+a)]2的圆方程,此时满足(7)式的参数a≈35.82.由梅花曲线构建的结构光束如图4所示.在图4(a)中,PED路径为圆形,其两个中轴线t1与t2同样为圆形.图4(b)展示了从PED路径对应到物理盘后的椭圆及其内外焦散线的结构分布.可见用于构建该光束的椭圆形状相同,只是旋转的角度不同.其内焦散线与外焦散线分别对应于洋红色以及深蓝色曲线.根据(9)式构建得到光强分布(图4(c))与相位分布(图4(d)),可以证明该光束即为拉盖尔-高斯光束[16].由于选择参数N=45,n=15,则光束对应的径向量子数p=n=15,角向量子数l=N−2n=15,符合拉盖尔-高斯光束的波动方程公式所计算的结果.

图4 b=0梅花曲线构建的结构光场 (a)PED内梅花曲线变为圆,t1与t2为同心圆;(b)物理盘上椭圆的分布;(c),(d)分别为(9)式构建得到的光束束腰上光强与相位分布,该光束同时也是轨道量子数l=15、径向量子数p=15的拉盖尔-高斯光束Fig.4.A structured beam with b=0:(a)The Plumblossom curve turns into circle.Medial axes t1and t2are concentric circles;(b)ellipses in physical disk;(c)the intensity pattern;(d)the phase pattern.This is also known as a Laguerre-Gaussian beam with l=15 and p=15.

3.2 b=1的结构光束

当b=1时,a≈27.42,梅花形结构光束如图5所示.梅花曲线(3)式退化为图5(a)中的心形线.由于此时(3)式中参数a的值相对正弦部分很大,且正弦部分变化缓慢,故心形线趋向于一个圆.中轴线t1近似为一个离心率很小的椭圆,中轴线t2集中在单位圆的圆心附近,近似为一个点.其光束外焦散线q1近似为离心率很小的椭圆,内焦散线q2汇聚至两个点如图5(b)所示.光束光强分布在内焦散线附近明显处于峰值,如图5(c)所示.由于光线与这两条焦散线相切,光波沿着这两条三维内焦散线相干叠加,使得光束具有局部无衍射特性.

图5 b=1时梅花曲线构建的光束 (a)PED路径为紧贴单位圆的心形线;(b)物理盘内椭圆及其焦散线分布情况;(c),(d)光束束腰面上的光强与相位分布;注意到光强在内焦散线附近变强Fig.5.Structured beam with b=1:(a)The plumblossom curve is turned to be a heart curve;(b)ellipses in physical disk,the inner caustic is then concentrating to two points which make beam having nondiffraction feature;(c)intensity pattern;(d)phase pattern.Noticed that the intensity near the caustic becomes stronger.

我们采用角谱衍射计算图5构建的光束在yoz面上传播的光强分布,并使用光线的起点与终点两个端点表示光束在xoy面上的光线分布,以此来演示光束的自修复性质.如图6所示,在图6(a1)的两个焦散线处的光斑光强在一定范围内保持不变.在束腰面上,光线的起点与传输方向由(2)式确定.图6(a2)为光束束腰平面内光线传播的起点分布,图中使用深蓝色点表示处于光束内部的光线端点,由内向外逐渐变绿.由于光线是倾斜的,随着光束传输至z=500µm处,如图6(a3)所示,内部光线逐渐转移到光束外部,而光束外部的光线逐渐转移到光束内部,正是这种光线的转移使得光束出现了自修复的特性.视频mov3.avi展示了光线的转移过程.当遮挡住光束中心位置时(遮挡半径r<30µm),如图6(b1)所示,随着光束的传输,光束中心的光斑逐渐恢复.这一被遮挡的光束空间传播过程用光线表征,如图6(b2)与图6(b3)所示.当遮挡住中心的光线(图6(b2)),随着光束的传输,有来自周围的光线填补中心光线的空缺(图6(b3)),使光束自我修复.当遮挡住光束周围的环形区域(r>30µm),如图6(c1)所示.由于此时遮挡区域与图6(b1)的遮挡区域互补,故图6(c1)的光场与图6(b1)的光场满足巴比涅原理[22],即图6(c1)的光场与图6(b1)的光场叠加和等于图6(a1)的光场分布.图6(c1)中被遮挡光束的光线表征如图6(c2)与图6(c3)所示.注意到图6(c2)与图6(b2)以及图6(c3)与图6(b3)的光线分布也是互补的.与图6(b2)相反,图6(c3)中间部分的光线没有被遮挡,随着这些光线传播到z=500µm,光线分布逐渐由内部转移到外部,如图6(c3)所示.由于内部光线减少,光束内部的光强也减弱了.此外由于光束发散,光线密度减弱导致光强下降.

图6 b=1时结构光束的局部无衍射与自修复特性 (a1),(b1),(c1)光束在真空中传输yoz截面的光强分布图,(a1)无遮挡,光线演化过程参考视频mov3.avi;(b1)遮挡r<30µm的圆形区域;(c1)遮挡r>30µm的区域;(a2),(b2),(c2)与(a3),(b3),(c3)分别为xoy面上光线端点在z=0与z=500µm处的分布图;光线的分布演化直观地解释了光束的自修复特性Fig.6.Non-diffraction and self-healing properties of structured beam with b=1.(a1),(b1),(c1)Are intensity patterns of light beams(in vaccum)in yoz plane:(a1)not blocked,see also mov3.avi;(b1)r<30µm is blocked,the intensity pattern gradually heals under beam propagating;(c1)r>30µm is blocked.(a2),(b2),(c2)and(a3),(b3),(c3)Are ray distribution of beam in z=0 and z=500µm plane,respectively.The evolution of ray distribution gives an intuitionistic explanation of self-healing process.

从光线的角度来看,光束的中心部分的自修复特性是由来自外部的光线填补所产生的.当遮挡了光束周围区域后,光束失去了自修复能力.其他拥有内焦散线的光束都可以用这种光线的方式来解释其自修复特性[16].

3.3 b=5的结构光束

选取b=5,a≈27.42,该结构光束见图7.PED路径如图7(a)所示,梅花曲线为五瓣梅花形.其光束焦散线如图7(b),外焦散线构成光束的轮廓,内焦散线呈十角星状使光束具有较强的自修复能力.光束束腰面光强如图7(c),洋红色曲线为内焦散线,蓝色曲线为外焦散线,由于干涉形成了10个主瓣的强度分布.相位分布见图7(d),光束相位随方位角变化,则光束具有相位涡旋,其光子携带轨道角动量.

图7 b=5的结构光束 (a)PED内的五瓣梅花曲线,t1和t2曲线分别由深蓝色与洋红色标出;(b)物理盘内椭圆分布及其十角星包络线;(c),(d)分别为光场束腰面的光强与相位分布;光强在内焦散线附近变强Fig.7.Structured beam with b=5:(a)PED path is a fivepetal plum-blossom curve,t1is deep blue,and t2,magenta;(b)ellipses in the physical disk and their inner envelope curves,which form a decagonal star structure;(c)the intensity pattern;(d)the phase pattern.The intensity near the caustic becomes stronger.

图8 5瓣梅花曲线构建光场的自修复特性 (a1),(a2)为光束在无遮挡的情况下传输;(b1),(b2)遮挡光束中心r<30µm的区域;(c1),(c2)遮挡r>20µm 后的光场传输情况Fig.8.Self-healing property of structured beam with b=5:(a1),(a2)Non-blocked;(b1),(b2)r<30µm is blocked;(c1),(c2)r>20µm is blocked.(a2),(c2)demonstrate the self-healing property of this beam.

光束的自修复特性如图8所示.图8(a1)表示光束在束腰面的光场分布,这里使用光束束腰面最大光强归一化光束光强分布.随着光束传播一个瑞利距离后,光束发散使得光强明显减弱(图8(a2)).当束腰面中心部分被遮挡后如图8(b1),光强分布中心被遮挡了,在光束传播一个瑞利距离后如图8(b2),由于自修复性质,光束中心图案重新出现,而光束周围部分由于中心的遮挡逐渐减弱.当束腰面光束中心外部被遮挡后如图8(c1)所示,由于光束周围被遮挡,只留下中心光斑.光束传播一段距离后,如图8(c2)所示,周围的光束样式依然能自修复.而由于光束周围被遮挡,使得光束中心逐渐消失,同图6(c3)的分析.由于图8(c2)的光强较弱,为了方便读者观察并没有做归一化光强处理.

4 结 论

光线庞加莱球法结合复杂的几何曲线能设计出形态各异的结构光束,这类光束具有复杂的几何外形与焦散线结构,拥有一些新奇的传输特性,例如自修复特性、局部无衍射特性等.清晰的焦散线形状使人们能够更直观地观察光束的光斑分布以及预测光束在传输过程中的演化.此外光线庞加莱球法还给出了光束的光线描述,赋予了光束自修复性或无衍射性质的几何光学解释,使光束的这些特殊性质变得更加直观.焦散线与光线的几何关系[23]使得人们能可视化地设计具有这些特殊性质的光束[4,21].由于这些光线均是在实数三维空间传输,满足几何光线光场的传输规则[24].在均匀介质中光线沿着(2)式光线方向直线传播,并可以结合四元数[25]等空间光线追踪的方法来表征光束经过一阶光学元件,例如ABCD矩阵之后的变换.在非均匀介质下人们亦可通过光线方程以及程函方程(eikonal equation)[13]来描述光束在非均匀介质中的传输过程.对于光束经过衍射元件,可结合几何光学衍射理论[26,27]计算衍射光场.

本文仅仅展示了使用梅花曲线设计的结构光场.由于光线庞加莱球法几乎可以使用任意满足量子化条件((5)和(7)式)的PED路径进行结构光场的设计,除了梅花曲线还可以选择其他更加复杂的二维曲线作为PED路径以此设计出光场与相位更加复杂的结构光束.这类具有复杂的光强与相位结构的光束,在激光俘获与信息传输上有潜在的应用价值.由于光线庞加莱球法构建出结构光束束腰面上的复振幅(振幅与相位)分布,人们可以在4f系统中使用空间光调制器生成这类光束,这将为实际应用提供极大的便利.