精密回转类零件磨削制备实验研究

闫如忠，熊学文

（东华大学 机械工程学院，上海 201620）

1 引言

在现代制造工业领域，回转类零件是最基础的零件，无论是在飞机、汽车等应用领域，还是在车床、磨床等加工领域，都有十分广泛的应用，如飞机的起落架、汽车发动机曲轴、机床的主轴等，都是典型的回转类零件，这些零件的性能直接影响到整个机器的性能。随着制造技术的不断发展，对各种机械零部件的精度要求也不断的提高[1]，尤其是在装配过程中参与配合的轴承内外圈的形状精度以及轴类等回转类零件的加工精度，对装配精度有很大的影响，在机械装配过程中该类回转类零件的形位精度直接影响回转体的定位精度，进而使整机回转误差加大。对回转类零件的研究在提升机器的工作性能、加工精度和提高机器的使用寿命等方面均有很大的帮助，回转类零件正受到越来越广泛的关注。

传统精密回转类零件的制备主要依靠高精度的精密机床制备。由于高精度机床成本高昂，使得工件加工成本居高不下，同时由于技术限制和技术壁垒等原因，高精度机床研发周期长，更新换代需要耗费大量的人力物力，尤其对于小批量回转类零件的制备更是如此，因此迫切需要一种能在普通机床上制备高精度回转类零件的方法。

2 精密磨削研究现状

国外对于精密磨削的研究起步较早，以美国50年代末开发的单点金刚石切削（SPDT）技术为标志[2]，精密超精密加工技术得到了飞速的发展。文献[3]生产的超精密磨床，能够制备几何精度0.1μm，表面粗糙度Ra为5nm的工件。日本大森整教授于90年代初提出了砂轮在线修整技术（ELID），并利用该修整技术对单晶硅进行磨削，获得了表面粗糙度值Ra0.329nm的工件表面[4]。

我国对于精密超精密技术的研究主要集中在高校和科研院所。国防科大研制的非球面加工机床可加工最大口径为650mm的光学玻璃，并能够获得表面粗糙度达到纳米级别工件表面[5]。某研究所研制成功的Nanosys-300曲面加工机床能够制备表面粗糙度Ra值小于10nm的非球面零件，实现了非球曲面的超精密加工[6]。另外，国内重点大学及科研院所在精密超精密加工领域都进行了一定的研究[7]，并取得了突出的研究成果。

3 微粉磨削机理及去除率分析

3.1 微粉磨削机理研究

磨削过程是许多的磨粒共同作用的结果，每一颗磨粒都可以看成是一把微小的切削刃，磨削工件表面的形成是参与磨削的各独立磨粒共同作用的结果[8]。在实际磨削过程中，根据切屑形成机理的不同，可将砂轮磨削过程中产生的切屑分为两类，一类是由于磨粒切削刃与工件表面发生碰撞从而使工件表面发生脆性断裂而产生的切屑，另一类为磨粒的挤压使工件表层产生应力集中而发生碎裂所产生的切屑。其中碰撞剪切为磨削过程中切屑产生的主要形式。

微粉砂轮的磨削工况按切削进程可分为如下几个过程。在初始磨削阶段，由于磨粒切削边缘锋利且工件表面不平整性大，工件表面形貌凸凹明显，此时磨粒主要以碰撞的形式使工件表面凸起发生碎裂[9]。而在磨削中后期，由于磨粒发生磨钝现象及工件表面趋于平整，磨粒主要通过挤压，滑擦等作用形式使工件表面产生裂纹并最终形成切屑。在微粉磨削过程中，除了会形成切屑外，由于磨粒切削深度的不同在工件表面还会产生下列现象。

当磨粒刚进入工件表面或者切削深度较小时，工件表面主要以弹塑性变形为主，此时磨削力的切向分力小于磨削力的径向分力，磨削过程以滑动摩擦为主。当磨粒进入工件表面深度大于工件的临界切削深度时，切削力的切向分力会快速加大，当该切削力大于工件表面的抗剪强度值时，磨粒会对工件表面进行剪切运动，工件表面金属会形成切屑从工件表面剥离，同时还会伴有微裂纹产生。在精密加工过程中，选择适宜的磨削深度能够很好的将滑擦切削和剪切去除切削相结合，获得理想的加工表面。

3.2 材料去除率的计算

磨削工件的材料去除率表征了砂轮及各磨削参数综合作用的结果，是制定磨削相关参数的重要指标。1927年Preston提出了著名的Preston方程[10]，得出了磨削过程中材料去除率与磨削压力、磨削速度、及磨削时间成正相关性。在本课题研究过程中计算工件材料去除率时，以工件修整前后的体积差来表征工件的材料去除率。现取工件的一段微小截面进行计算分析，其示意图，如图1所示。图中阴影部分即为该截面去除区域，组成阴影部分的两条曲线即为磨削前后工件的轮廓曲线。

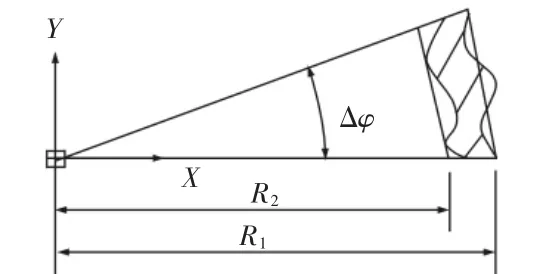
图1 工件截面微小取样Fig.1 Tiny Sampling of Workpiece Cross-Section

当图1中的取样角度足够小时，其阴影部分可近似用矩形来代替，其中矩形的长度可由两曲线的中线圆弧长度来近似由弧长计算公式可得。在图1中两段圆弧的中线长度可近似表示为：

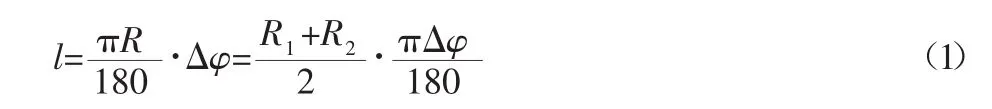
式中：R1、R2—磨削修整前后工件上轮廓点到基准圆心的距离。

则该微小区域的面积表示为：

因此，工件在整个测量截面的材料去除面积可用各小区域面积之和表示。

式中：h、t—实验过程中工件的加工宽度及加工时间。

因此，磨削加工过程中的材料去除率可表示为：

4 实验修整装置

为了研究在传统实验装置上进行精密加工的可行性，实验以MG1432A磨床为实验平台，并对其进行了一定的改装，改装后的磨削修整装置图，如图2所示。该套实验装置主要包括砂轮、工件、压力调节装置、平衡调节装置、拨盘、伺服控制系统等。伺服电机通过拨盘与加工工件相连，在实验中实现对加工工件的转速控制，从而实现工件的误差补偿。砂轮通过同步带与变频电机相连，维持稳定的切削速度。磨削压力则由压力调节块调节，压力调节块由许多的钢珠组成，在实验过程中可通过增减钢珠的数量实现磨削压力的控制，从而控制实验过程中的磨削去除量。平衡配重块也是由钢珠袋组成，其作用是保证在未添加压力调节块时磨削砂轮刚好与工件接触，但未有接触压力。

图2 磨削修整装置二维示意图Fig.2 The Grinding Dressing Device 2D Schematic

5 实验修整原理及实验结果

5.1 实验修整原理

为了制备满足精度要求的回转类零件，在其制备过程中需要对工件进行多次磨削修整和多次测量，直至其满足加工要求为止，实验过程中的磨削修整流程图，如图3所示。

为了实现在传统磨床上获得高精度回转类零件，在零件磨削过程中采用圆度逼近理论进行磨削修整。在磨削修整前先对工件表面轮廓进行测量，从而获得工件轮廓上各点的法向残余误差，根据工件上各点的法向误差值设定各点的磨削修整速度，将法向误差补偿转化为工件速度补偿，从而不断逼近理论轮廓，使工件的实际轮廓趋于平缓，达到提高工件圆度的目的，其逼近过程，如图4所示。通过多次逼近修整，使工件法向误差收敛，从而使其实际轮廓曲线不断趋近于理论轮廓。

图3 磨削修整流程图Fig.3 Grinding Dressing Process Flow Chart

图4 磨削修整阶段试件轮廓线性展开曲线Fig.4 The Workpiece Contour Linear Curve During the Period of Grinding

实验采用工件速度补偿代替法向误差补偿进行圆度逼近。通过给定不同转速实现工件不均匀去除，从而实现工件误差补偿。在法向误差大的地方，需要进行大的误差补偿，因此需要降低工件转速，提高工件与磨具的接触时间，从而产生大的工件去除量。在残余误差小的地方，需要的误差补偿小，提高工件的转速能够减小工件与磨具的休整时间，从而减小工件的去除量。为了防止冲击和振动，在速度控制过程中其变换过程应该是连续的，从而实现平缓过渡。根据误差补偿原理需要对工件各点进行不均匀去除。加工前所测得的工件表面轮廓曲线，如图5所示。由图中可看出工件上1，2，4，6，7处工件径向误差较大，需要大的误差补偿，因此在这几处区域需要设置低的工件转速，从而加大该区域材料去除量。而在工件轮廓3，5，7处误差较小，需要较高的转速减小去除量，从而实现小的材料去除量。通过对工件进行不均匀去除修整，加快工件径向误差收敛。

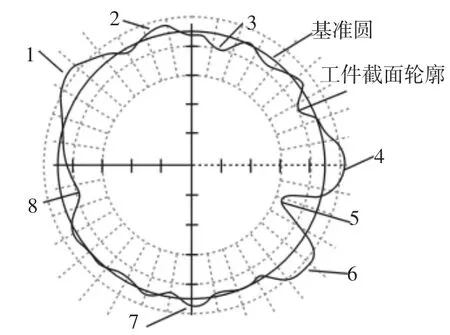
图5 工件截面轮廓曲线Fig.5 The Contour Curve of Workpiece Cross-Section

5.2 实验结果

由上述修整原理对直径为125mm的GCr15回转类零件进行磨削实验，选用W3.5-W10的铬刚玉微粉作为修整磨具，修整砂轮转速为（300～500）r/m，磨削压力为（3.5～15）N，经过多次磨削修整实验后使用圆度仪对工件轮廓再次进行测量，其测量装置图，如图6所示。将实验所测得的工件轮廓曲线进行线性展开，其修整前及磨削修整实验结束后的轮廓线性展开曲线，如图7所示。由测量结果可以看出，经过多次磨削修整后，工件的圆度从10.34μm改善至0.35μm，加工精度得到了很大的改善。通过本实验结果可知，工件试样在经过多次磨削修整后其圆度达到了实验要求，实现了在普通磨床上对精密回转类零件的制备。

图6 测量装置图Fig.6 The Measuring Device

图7 磨削修整前后工件轮廓线性展开曲线Fig.7 Workpiece Contour Linear Curve Before and After Grinding

6 结论

（1）回转类工件的径向误差可以采用圆度逼近理论进行收敛。通过多次逼近修整可以使工件实际轮廓与理想轮廓的径向误差收敛于某一给定值，从而达到希望的精度。（2）工件法向误差补偿可以转化为工件的速度补偿。由于速度补偿较误差补偿简便，在误差补偿过程中可用速度补偿以获取不均匀去除量，进而实现工件误差补偿。（3）通过误差补偿及圆度逼近理论，在普通磨床上制备高精度回转类零件是可行的。