半波长交流输电柔性调谐的控制策略与仿真分析*

王鑫，戴朝波，李琳，赵国亮，孙谊媊，于永军

(1.华北电力大学 电气与电子工程学院，北京 102206； 2.先进输电技术国家重点实验室(全球能源互联网研究院)，北京 102209； 3.国网新疆电力公司电力科学研究院，乌鲁木齐 830011)

0 引 言

我国西部能源供给中心与东部能源需求中心之间距离达2 000～3 000 km，所以需要超远距离、超大容量的电力输送技术。半波长交流输电技术作为一种超远距离、大容量输电技术方案，是支撑跨国、跨洲输电的有效途径之一，具有较强的优势[1-5]。

半波长交流输电(Half Wavelength AC Transmission，HWACT)是指输电的电气距离接近1个工频半波长，即3 000 km(50 Hz)或2 600 km(60 Hz)的超远距离三相交流输电。根据传输线理论，均匀无损的半波长传输线的首端和末端具有相同的电压幅值及输入阻抗。半波长交流输电可实现点对点输电，全线中途不需要设置开关站，无需安装无功补偿设备，线路输电能力强[6-11]。

受客观条件限制，实际线路的自然长度难以正好是半个波长。当输电线路长度不足半波长时，需要对线路进行人工调谐，以达到人造半波长输电线路的目的。文献[12]提出了无源π型、T型调谐的参数计算公式，文献[13]计算分析了均匀电容型的调谐，仿真结果表明可以达到人造半波长输电的目的。上述无源调谐存在对系统结构、运行方式和参数变化的适应性相对较差，容易失去半波长特性等问题。本文提出了一种π型半波长输电柔性调谐装置，该装置不仅具有调谐功能，还能灵活适应系统结构、运行方式和参数的变化，并且还具有功率因数灵活补偿、实现柔性并网、抑制线路过电压、阻抗匹配等无源调谐网络所不具备的功能。

文中详细介绍了所提出的π型半波长输电柔性调谐装置，并设计了相应的控制策略。应用现有特高压交流线路的参数在PSCAD/EMTDC中搭建了半波长交流输电柔性调谐仿真等值系统，并对柔性调谐装置的调谐效果及功率因数补偿效果进行了仿真分析。

1 半波长输电线路调谐的基本原理

1.1 无源型调谐网络

双电容、单电感的π型调谐网络如图1中所示。在忽略线路损耗的情况下，只要调谐网络与被调谐的线路具有相同的转移参数矩阵，就不会影响线路其他部分的电压、电流分布，据此，可以计算出相应的电感和电容值[12]。显然，无源π型调谐网络的参数不能变化，对系统结构和运行方式的适应性相对较差。

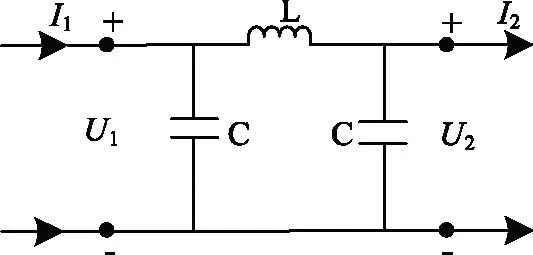
图1 π型调谐网络Fig.1 π type tuning network

1.2 柔性调谐

π型半波长输电柔性调谐装置如图2所示，包括串联调谐器及其两端的并联调谐器。如线路长度小于一个工频半波长，串联调谐器等效为一个串联电感，用来实现半波长柔性调谐所需要的电感。并联调谐器等效为一个并联电容，用来实现半波长柔性调谐所需要的电容。如果输电线路结构、参数和运行方式发生变化，可以调整串联调谐器的等效电感值和并联调谐器的等效电容值，从而满足变化后的半波长交流调谐需求，即实现了柔性调谐。

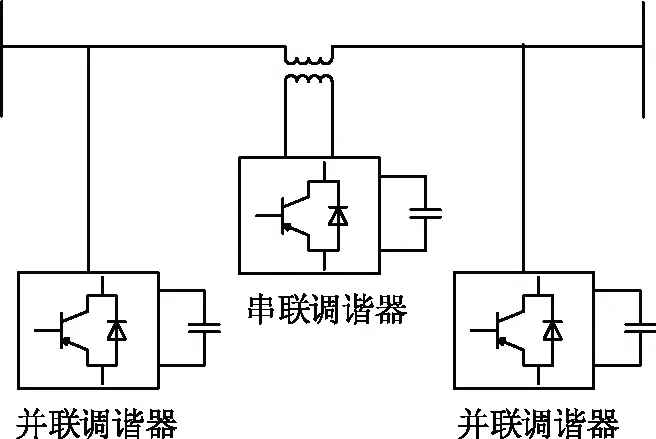
图2 π型柔性调谐装置Fig.2 π-tuning flexible device

柔性调谐装置不仅具有调谐功能，还可以具有灵活补偿功率因数这一无源型调谐网络所不具备的功能。当半波长线路送端功率因数不为1，且无功功率经过半波长输电线路由送端传输到受端，此时安装在输电线路受端的柔性调谐装置中远离受端系统的并联调谐器仅参与调谐，而和受端系统较近的并联调谐器可以根据系统所要补偿的无功功率，控制相应的输出，同时满足调谐和补偿功率因数的这两个要求。如果送端系统的功率因数发生变化，该并联调谐器也随之调整，进而使其同时满足调谐和补偿功率因数的这两个要求。

2 柔性调谐的主电路结构及控制

2.1 串联调谐器的主电路结构

在不影响论证柔性调谐的作用和效果的前提下，如图3所示，串联调谐器采用简单的单H桥结构，具体包括三个单相的电压源型逆变器，并通过Y/Y耦合变压器串联在输电线路中。图中，usa、usb、usc为串联调谐器的输出电压；isa、isb、isc为流经串联调谐器的线路电流；L为每相的滤波电感；C为输出滤波电容；Cdcsa、Cdcsb、Cdcsc为直流侧电容；Udcsa、Udcsb、Udcsc为直流侧电压。

2.2 串联调谐器的控制策略

串联调谐器的控制目标是向输电线路注入一个相位超前线路电流90°的电压，使其呈现电感特性，进而实现半波长柔性调谐。实际上，考虑逆变器和变压器的损耗，串联逆变器必须从系统吸收部分能量来补偿损耗，维持直流母线电压稳定，这样，输出电压就不会与电流完全垂直，偏移的角度是为了保证串联调谐器能够从系统中吸收相应的能量。

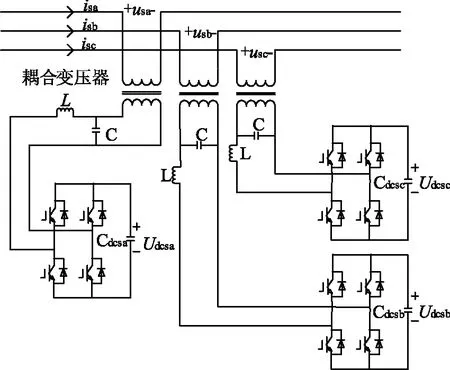
图3 串联调谐器的主电路结构Fig.3 Main circuit topology of series tuner

串联调谐器采用输出阻抗控制，相应的控制框图如图4所示。

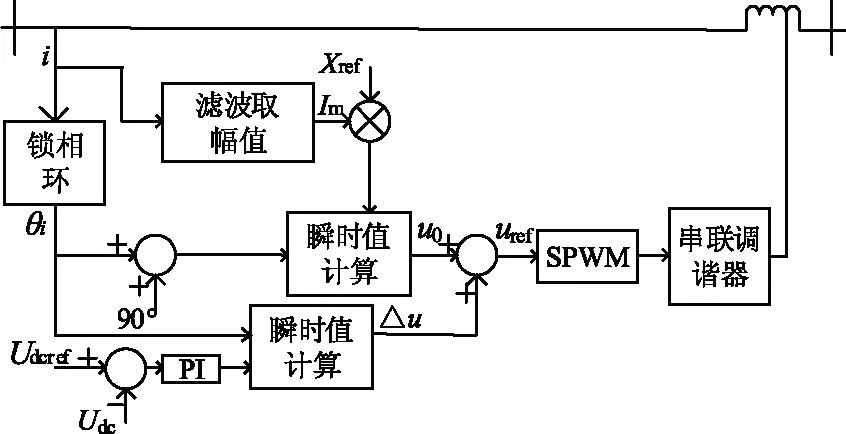
图4 串联调谐器的控制系统框图Fig.4 Control block diagram of series tuner

参考阻抗Xref可由半波长柔性调谐需要的电抗值减去输出滤波器中的电抗值得到。θi是由线路电流i通过锁相环得到的，θi加上90°便得到了u0的相角；串联调谐器注入电网电压的幅值与线路电流的幅值成正比，即：

Um=XrefIm

(1)

式中Im由线路电流i经过低通滤波后，通过计算获得。

图中控制策略还包括直流侧电容电压稳定控制，直流电压误差信号通过一个比例积分控制器得到一个与线路电流同向的电压偏移量Δu。当Δu很小时，其大小决定了逆变器与系统间存在很小的有功交换，这个功率等于直流电容器的充放电功率及逆变器回路的损耗，通过控制此电压即可实现对直流电容电压的控制。电压u0与电压偏移量Δu叠加后便可以得到电压的参考值信号uref，进而通过正弦脉宽调制技术对串联调谐器实施控制。

2.3 并联调谐器的主电路结构

基于同样的原因，柔性调谐中的并联调谐器采用了简单的三相桥结构，其主电路结构如图5所示，ia、ib、ic为并联调谐器的输出电流；Ea、Eb、Ec为并联调谐器与线路连接处电压；Lf为逆变器侧滤波电感；Lg为网侧滤波电感；Cf为滤波电容；Rf为阻尼电阻；Lf、Lg、Cf、Rf构成并联调谐器交流侧输出LCL滤波器；Cdc为直流侧电容；Udc为直流侧电压。

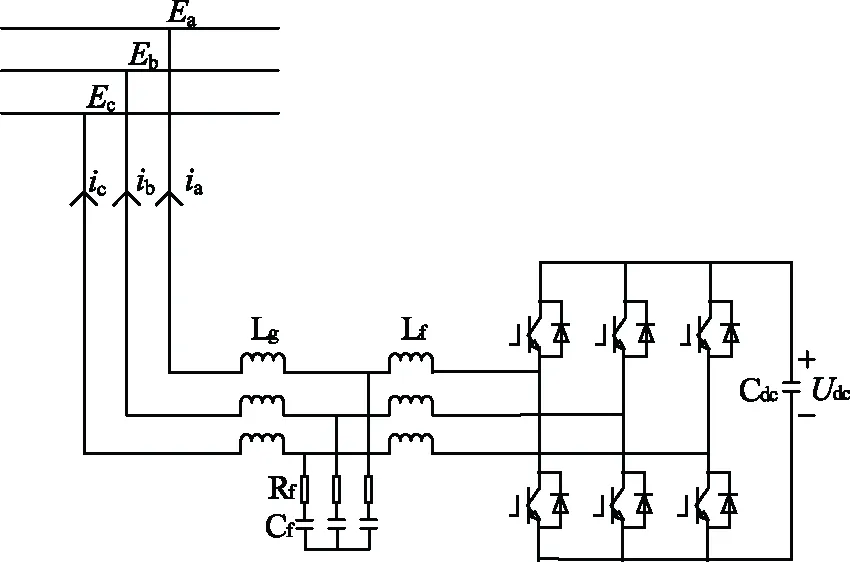
图5 并联调谐器的主电路结构Fig.5 Main circuit topology of parallel tuner

2.4 仅参与调谐的并联调谐器的控制策略

并联调谐器采用电流跟踪型PWM技术对电流波形的瞬时值进行反馈控制。其中，PWM控制信号是采用三角波比较方式获得。相应的控制框图如图6所示。

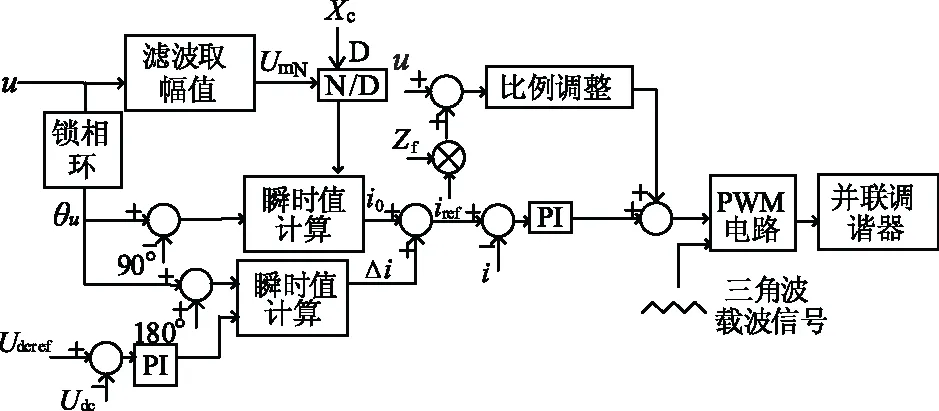
图6 仅参与调谐的并联调谐器的控制框图Fig.6 Control block diagram of parallel tuner only involved in tuning

图6中θu是由并联调谐器与线路连接点处的电压u通过锁相环得到的，然后θu减去90°便得到了i0的相角。

而并联调谐器注入线路中的电流幅值与连接点处电压幅值的关系：

(2)

式中Xc是并联调谐器参与半波长柔性调谐所需要的容抗值；Um由连接点电压经过低通滤波后，通过计算获得。

图中控制策略还包括直流侧电容电压稳定控制，直流电压误差信号通过一个比例积分控制器得到一个与线路电压成反向的电流偏移量Δi。通过控制此电流即可实现对直流电容电压的控制。电流i0与电流偏移量Δi叠加后便可以得到补偿电流的参考信号iref，实际的补偿电流i与参考信号比较之后进行比例积分，然后与引入的前馈电压u相加得到调制波信号，最后再与高频三角载波相比较，产生并联调谐器所要求的开关信号。

2.5 同时参与调谐和功率因数补偿的并联调谐器的控制策略

并联调谐器不仅可以参与调谐，还可以参与送端系统功率因数的补偿，其控制框图如图7所示。在仅参与调谐的并联调谐器的控制策略基础上改进了注入线路电流的幅值。

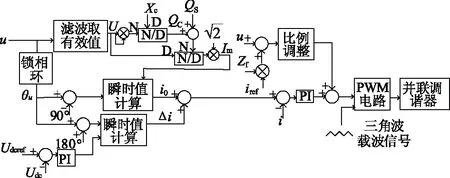
图7 具有功率因数补偿的并联调谐器的控制框图Fig.7 Control block diagram of parallel tuner with the power factor compensation

具体地，并联调谐器参与调谐所需补偿的无功功率为：

(3)

式中Xc是并联调谐器参与半波长柔性调谐所需要的容抗值；U是由连接点电压u经过低通滤波器并通过计算得到的。

检测到的送端系统输出的无功功率为QS，与QC相加便得到了并联调谐器实际需要补偿的无功功率，根据并联调谐器补偿无功与其注入到线路中电流幅值的关系：

(4)

这样，便可以得到注入到电网中的电流幅值。

3 仿真及分析

3.1 系统模型及参数设置

利用PSCAD仿真软件建立了自然半波长输电线路及采用无源π型调谐网络、π型柔性调谐装置的半波长线路仿真模型，如图8所示。根据我国第一条特高压输变电工程——1 000 kV晋东南-南阳-荆门特高压交流输变电试验示范工程所选线路型号，输电线路仿真模型的导线均采用8分裂LGJ-500/35型钢芯铝绞线，且子导线呈正八角形排列；地线均采用JLB20A-170型铝包钢绞线。PSCAD中输电线路采用相频模型。自然半波长输电线路全长为2 938.1 km，为了测量相应线路的电压和电流值，设置12个电压和电流测量点；约定采用无源π型网络、π型柔性调谐装置的线路长度为2 138.1 km，调谐装置配置于线路两端，且各补偿400 km，设置11个电压和电流测量点。

图8 不同形式的半波长线路Fig.8 Different forms of half wavelength lines

送端交流系统均采用三相理想电压源，送端变压器的变比为20/1 050 kV，变压器容量为7 200 MVA，漏抗为18%；受端采用1 000 kV等值电源，具体参数如下：零序电阻为3.166 Ω，零序电抗为28.452 Ω，正序电阻为0.814 Ω，正序电抗为10.392 Ω。

根据参考文献[12]中的计算方法，可以得到采用无源π型调谐网络的半波长线路参数为固定电容值C=2.798 μF，固定电感值L=0.323 H。

根据参考文献[14-16]中的计算方法可以得到π型柔性调谐装置的相关仿真参数。

图8(c)中的四个并联调谐器的参数相同，具体如下：直流侧电压：Udc=2 100 kV，直流侧电容：Cdc=100 μF。逆变器侧滤波电感：Lf=0.3 H，网侧滤波电感：Lg=0.02 H，滤波电容：Cf=0.13 μF，阻尼电阻：Rf=800 Ω。

图8(c)中两个串联调谐器的参数相同，每个串联调谐器的三个单相逆变器参数也相同，具体如下：直流侧电压：Udcs=450 kV，直流侧电容：Cdcs=350 μF。滤波电感：L=15 mH，滤波电容：C=2 μF。耦合变压器的容量均为10 000 MVA，变比均为1:1，漏抗均为0.001 p.u.。

3.2 仿真结果分析

3.2.1 调谐功能的仿真分析

不同形式的半波长线路沿线电压随功率的变化曲线如图9所示。曲线X1代表自然半波长线路，X2代表无源π型调谐线路，X3代表柔性π型调谐线路。x代表距半波长线路送端的距离，l代表自然半波长线路长度，带调谐网络的半波长线路以电气距离代替实际线路距离以方便与自然半波长线路沿线电压进行比较。

半波长线路的自然功率约为4 500 MW，由图9可得：传输功率等于自然功率时，全线路电压的幅值基本一致；传输功率小于自然功率时，线路电压分布呈两端高，中间低；传输功率大于自然功率时，线路电压分布呈两端低，中间高；如图9所示，1.2倍自然功率传输时，中点位置电压最高达1.17 p.u.。

当传输相同的功率时，采用无源π型调谐网络和采用π型柔性调谐装置的半波长线路与自然半波长输电线路的沿线电压变化趋势及幅值基本一致。

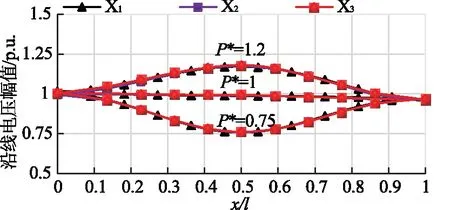
图9 传输不同功率时不同形式的半波长线路的沿线电压分布Fig.9 Voltage distribution along the different half wavelength lines with different power

不同形式的半波长线路沿线电流随功率的变化曲线如图10所示。由图10可以看出，沿线电流的变化趋势与电压相反，离半波长线路两端越近，线路电流受传输功率的影响越大，但线路中点的电流几乎不受传输功率的影响。

当传输相同的功率时，采用无源π型调谐网络和采用π型柔性调谐装置的半波长线路与自然半波长输电线路的沿线电流变化趋势及幅值基本一致。

图9、图10所示的结果验证了柔性调谐装置的可行性。

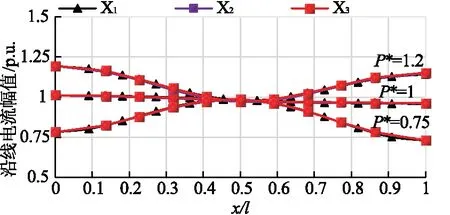
图10 传输不同功率时不同形式的半波长线路的沿线电流分布Fig.10 Current distribution along the different half wavelength lines with different power

为验证传输功率变化时控制系统的有效性，令输电线路上传输的功率在0～0.6 s时传输1倍自然功率、0.6 s～0.8 s时传输0.75倍自然功率。

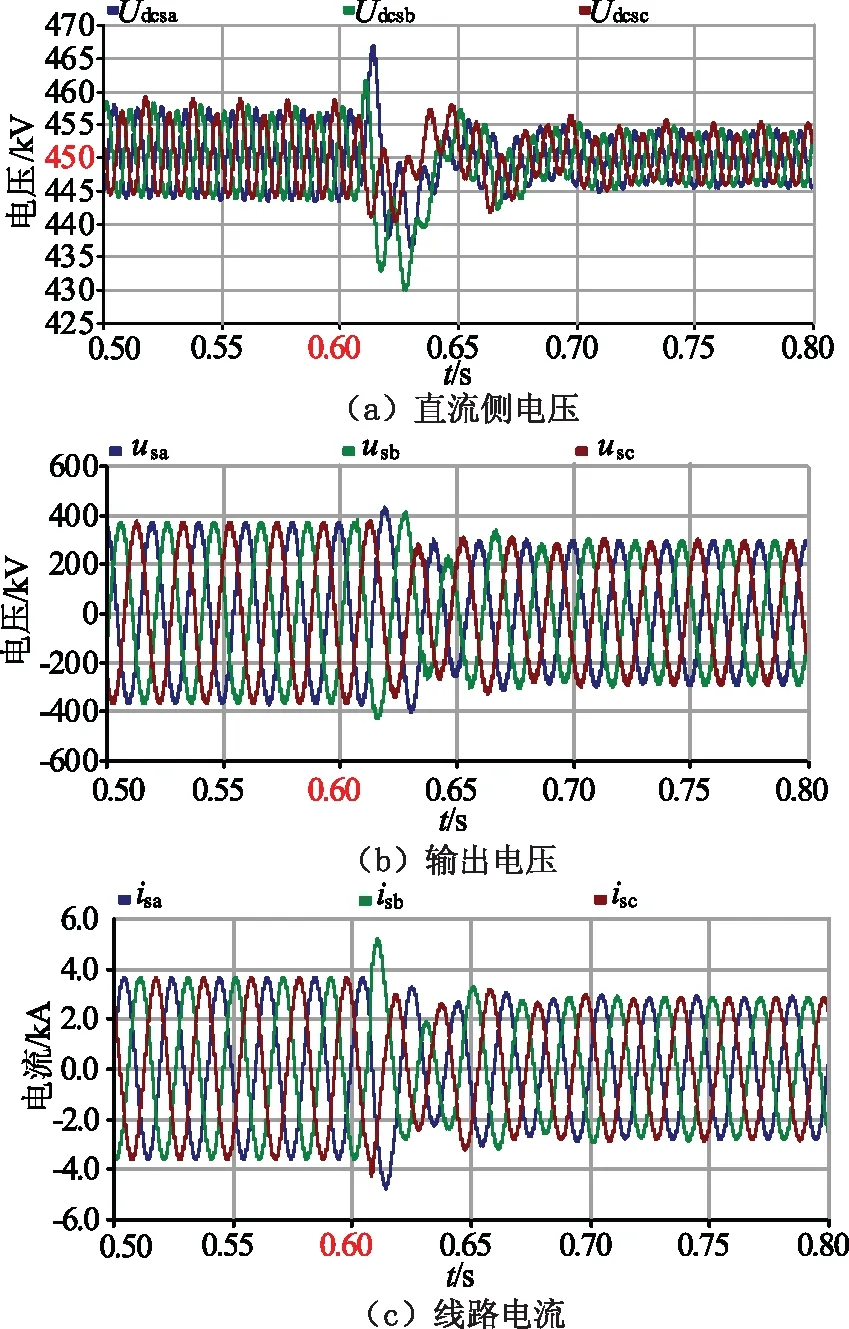
图11 串联调谐器1的交直流侧波形Fig.11 AC and DC side waveforms of the series tuner 1

由于两个串联调谐器的控制系统一致，四个并联调谐器的控制系统也基本一致，限于篇幅，只给出了在不同负载切换时，图8(c)中串联调谐器1和并联调谐器2的交直流侧的波形，如图11、12所示，随着传输功率的减小，串联调谐器直流侧电压波动的范围、输出电压和线路电流均显著减小，并联调谐器注入电流和连接点处线路电压略微减小，而直流侧电压也基本维持在2 100 kV左右；并且在传输功率发生变化时，串联调谐器和并联调谐器的控制系统均能够快速响应，使串联调谐器输出的电压和并联调谐器注入的电流快速跟随传输功率的变化。

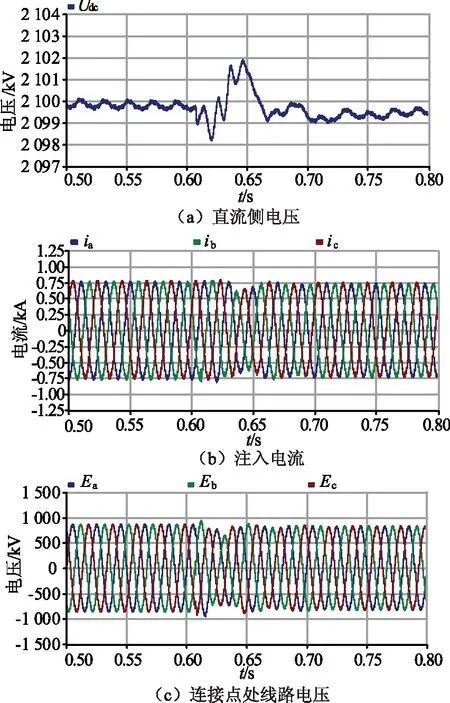
图12 并联调谐器2的交直流侧波形Fig.12 AC and DC side waveforms of the parallel tuner 2

在传输功率发生变化时，半波长线路送端和受端传输的有功功率如图13所示。P1、P2分别为送端系统输出的有功功率和受端系统吸收的有功功率，可以看出，在传输功率发生变化时，由于待调谐输电线路沿线存在电磁作用的推迟作用，所以受端有功功率的变化滞后送端大约0.007 s，送端和受端的有功功率在经过短暂的波动后也可以保持稳定。图11～图13所示的结果验证了串联调谐器和并联调谐器控制系统的有效性。

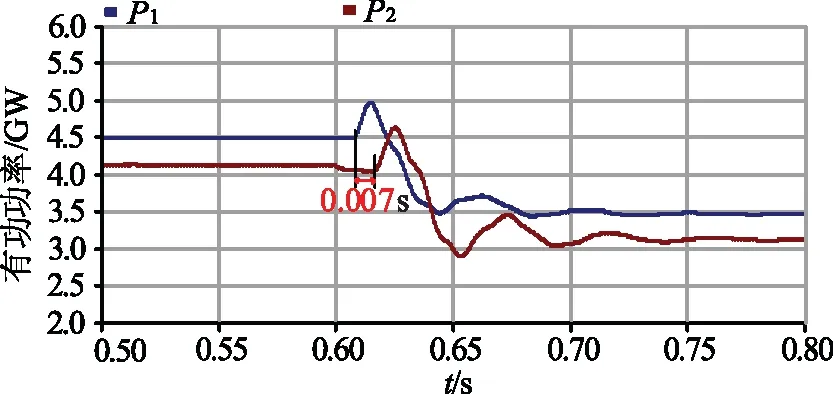
图13 半波长输电线路的有功功率Fig.13 Active power of half-wavelength lines

3.2.2 功率因数补偿功能的仿真分析

设半波长线路送端的有功功率为自然功率，而无功功率不为零，即功率因数不再为1；如图14所示的四条曲线：X1代表功率因数为0.9(感性)时，采用无源π型调谐网络的半波长线路沿线电压分布；X2代表功率因数为0.9(感性)时，采用π型柔性调谐装置未补偿的半波长线路沿线电压分布；X3代表受端π型柔性调谐装置进行功率因数补偿后的沿线电压分布；X4代表功率因数为1.0时，采用无源π型调谐网络的半波长线路沿线电压分布。

从图14中可以看出：当半波长线路传输感性无功功率时，沿线电压呈现出先降后升的趋势，沿线电压波动较大，线路最高电压出现的位置偏向末端，最高电压达1.27 p.u，因此要尽量避免无功通过半波长线路传送；采用无源π型调谐网络与采用π型柔性调谐装置未补偿的半波长线路沿线电压变化趋势以及幅值基本一致。

由于受端的π型柔性调谐装置可以进行功率因数的补偿，所以从图14中可以看出，在受端π型柔性调谐装置实施补偿后，半波长线路全线电压基本维持在1 p.u.左右，与采用无源π型调谐装置仅传输有功功率时的半波长线路沿线电压分布基本一致，避免了半波长线路沿线电压的波动。

图14 送端系统功率因数对不同形式半波长线路沿线电压的影响Fig.14 Influence of power factor on the voltage of different half wavelength lines

由图15可以看出，当送端系统功率因数为0.9(感性)时，采用无源π型调谐网络与采用π型柔性调谐装置未补偿的半波长线路沿线电流的变化趋势与电压相反，呈现先升后降的趋势，沿线电流波动较大。

而由于受端π型柔性调谐装置在进行功率因数补偿时要补偿受端系统吸收的无功功率，所以，π型柔性调谐装置参与补偿后的半波长线路受端电流要比采用无源π型调谐装置仅传输有功功率时的半波长线路受端电流大一些，而除受端外两线路沿线电流分布基本一致，基本维持在1 p.u.左右，避免了半波长线路沿线电流的波动。

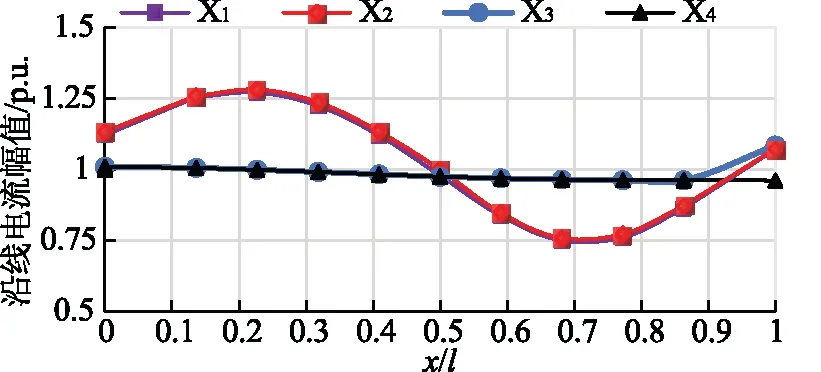
图15 送端系统功率因数对不同形式半波长线路沿线电流的影响Fig.15 Influence of power factor on the current of different half wavelength lines

4 结束语

建立了π型柔性调谐装置的模型，并结合并联调谐器和串联调谐器的主电路结构和工作原理，设计了半波长柔性调谐的控制策略。通过仿真分析得到了以下结论：

(1)在传输相同的功率时，采用π型柔性调谐装置的半波长线路与采用无源π型调谐网络的半波长线路以及自然半波长线路的沿线电压、电流分布基本一致，证明了π型柔性调谐装置的可行性；

(2)在传输功率发生变化时，串联调谐器和并联调谐器的控制系统均能够快速响应，使串联调谐器注入的电压和并联调谐器注入的电流快速跟随传输功率的变化，验证了π型柔性调谐装置控制系统的有效性；

(3)当送端系统功率因数不为1时，送端系统送出的无功流经半波长线路会引起沿线电压、电流的波动，经过受端π型柔性调谐装置的补偿，避免了沿线电压、电流的波动，实现了无源π型调谐网络所不具有的功率因数补偿的功能。

柔性调谐装置需要高电压大容量换流器，尽管按现有技术水平在工程上可以实现，但存在成本高，可靠性略差，运行维护要求高等问题。随着技术的不断发展,器件成本应该会大幅下降，考虑到柔性调谐装置具有柔性调谐、功率因数补偿、实现柔性并网、抑制线路过电压、阻抗匹配等诸多无源调谐网络所不具有的功能，未来将有可能得到应用。