基于改进两阶段鲁棒优化的区域综合能源系统经济调度*
单福州,李晓露,宋燕敏,周海明,刘超群
(1.上海电力学院 电气工程学院,上海 200090; 2.中国电力科学研究院有限公司,北京 100080)
0 引 言
随着经济的发展,化石能源日益枯竭,可再生能源以其储备丰富、分布范围广、环境危害低等特点,逐渐成为未来能源消费的主要方式。但是,可再生能源出力和负荷用电特性的随机性、波动性限制了新能源的消纳和电网安全经济运行[1]。因此,如何降低不确定性对系统日前发电计划安排、实时运行的影响已成为当前研究热点。
目前,一些文献已开始研究如何降低不确定性对系统的影响。文献[2]通过增加系统备用容量,来降低可再生能源出力波动的影响,以可再生能源出力预测误差的概率分布来确定备用容量的取值大小具有一定的盲目性。文献[3-5]采用基于概率分布的随机规划、机会约束规划等分析方法处理系统中不确定变量,但电力系统中波动频繁,不确定变量众多,很难获得较为精确的概率分布函数,影响方法的精确性。文献[6]采用场景削减来寻求相对精确的概率分布函数,降低随机优化算法的计算量,但场景削减不能涵盖系统内所有场景,仍然存在一定风险性。
鲁棒优化只需知道不确定参数的波动范围,通过一个不确定集合表征参数的波动,当在不确定集合中取值时,鲁棒优化模型就一定能得到确定的可行解[7]。相对于随机优化、机会约束优化来说,鲁棒优化无需获得其精确的概率分布,计算量明显降低。文献[8]建立min-max-min结构的经典两阶段鲁棒优化模型来求解最小化极端场景下系统运行成本,但极端场景发生概率较低,仅仅追求极端情况下系统运行成本最低,求得的解相对保守。
在上述背景下,提出了一种以期望场景下最优,任意场景下可行的改进两阶段鲁棒优化方法,在充分考虑可再生能源出力和用电负荷波动的基础上,建立了以日前经济调度成本和实时运行下的调整成本之和最小为目标的改进两阶段鲁棒优化经济调度模型。以冬季某区域综合能源系统为例,采用列约束生成算法对模型进行求解,对比分析以最坏场景下最优目标的经典两阶段鲁棒优化模型与该模型的优劣。结果表明,改进两阶段鲁棒经济优化模型能显著降低系统备用容量,提高系统运行经济性,更加贴合实际工程需求。
1 区域综合能源系统建模
综合能源系统(Integrated Energy System,IES)特指一种通过深度融合能源与信息技术,在规划、建设和运行等过程中,通过对能源的产生、传输与分配(能源供应网络)、转换、存储、消费等环节进行有机协调与优化,逐步形成以电力系统为核心,涵盖供电/热/冷/气等能源产供销一体化的复杂系统网络[9]。目前,对IES的研究通常以冷热电联供(Combined Cooling Heating and Power,CCHP)为研究对象,如图1所示,其中PV为光伏发电机组;BT为蓄电池;GT为微型燃气机;GB为燃气锅炉;EB、EC分别为电锅炉和电制冷机;AC为吸收式制冷机。
1.1 区域IES中设备模型
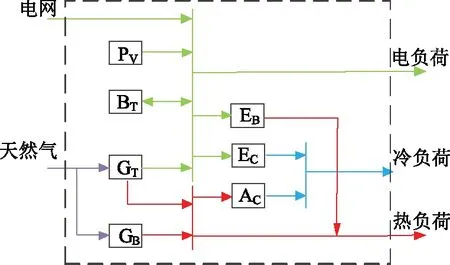
图1 区域IES中CCHP系统结构示意图Fig.1 Schematic diagram of CCHP system in regional IES


1.2 不确定性出力
由于气象因素的时变性,风电场实际出力将在日前预测出力周围上下波动,考虑光伏出力和电负荷不确定性对系统实时运行下调整成本的影响。不确定集合U为:

(1)

1.3 约束条件
(1)功率平衡约束
(2)
(2)蓄电池约束[12]
为了应对突发状况和延长蓄电池的使用寿命,不允许其深度放电。则储能容量约束:
(3)
蓄电池最大充、放电功率约束,且充、放电不能同时进行:
(4)
同时,在调度周期内应保持其始末时刻电能相等:
(5)
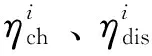
(3)备用容量约束[13]
(6)

(4)其余约束主要包括设备出力范围约束和联络线上、下限约束。其中,微型燃气轮机的功率响应速度相对于小时级别的调度而言较快,因此,不考虑其启停和爬坡约束[14]。
2 两阶段鲁棒优化调度模型及求解
2.1 经典两阶段鲁棒优化模型
经典两阶段鲁棒优化模型的基本思想是只要系统出力计划能抵御最极端场景下的扰动,就一定满足任意其他场景下的扰动。优化模型为:

(7)
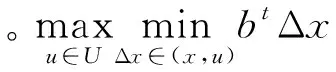
2.2 改进两阶段鲁棒优化模型
经典两阶段鲁棒优化模型求解极端情况下的最优目标,在一定程度上提高了系统的鲁棒性,但极端场景发生概率较低,仅仅追求极端情况下系统运行成本最低,系统备用成本相对较高,求得的解相对保守。针对经典两阶段鲁棒优化模型的缺点,提出改进两阶段鲁棒优化模型,其基本思想是系统出力计划在期望场景下最优,且能抵御任意场景下波动。该模型结构为:
(8)
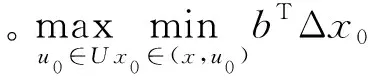
2.3 目标函数
根据对两阶段鲁棒优化调度模型的分析,以日前经济调度成本和实时运行下的调整成本之和最小为目标函数:
(9)

2.4 求解算法
针对上述提出的两种鲁棒优化模型,本文采用列约束生成(Column Constraint Generation,CCG)算法进行求解。CCG算法将两阶段鲁棒优化模型分解为主问题(MP)和子问题(SP)两个问题进行反复迭代求解,在求解过程中不断引入SP相关的变量和约束,获得更加紧凑的原目标函数值下界,从而有效降低迭代次数。
以经典两阶段鲁棒优化模型为例进行分解(改进两阶段鲁棒优化模型分解方法与此类似),得到MP为:
(10)
分解后得到的SP为:
(11)
SP内层最小化为线性问题,根据对偶理论可知,将其转换为max函数,并与外层max函数合并,可得如下等效SP:
s.t.DTλ+GTγ≤b
λ≥0,γ≥0
(12)
式中xk为第k次迭代时得到的MP的解;Δxk为第k次迭代时得到的出力变化量;λ、γ分别为最小化问题中各约束条件对应的对偶变量。
3 算例分析
以冬季某工业区综合能源系统的典型日为例进行优化分析,系统结构如图1所示。其中系统向配电网购电为正,反之为负;蓄电池放电为正,充电为负。本文根据历史数据,考虑光伏出力和电负荷波动偏差分别为15%和10%,光伏出力和电负荷的预测/实际出力曲线如图2和图3所示。

图2 实际/预测光伏出力曲线Fig.2 Actual/predicted PV curve
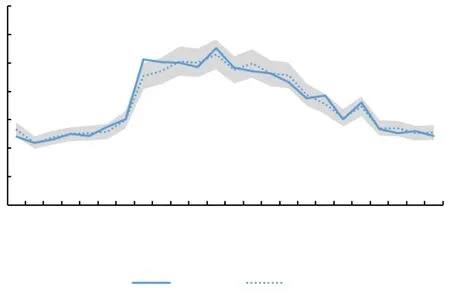
图3 实际/预测电负荷功率曲线Fig.3 Actual/predicted electric load power curve
3.1 区域IES优化结果
如图4示,在1 h~7 h和21 h~24 h,燃气轮机单位发电成本高于电网和光伏日前预测电价,系统主要从电网购电,此时微型燃气轮机以最小功率运行;在11 h~13 h,光伏出力在满足系统负荷时,将多余电量出售给电网,降低系统运行成本;在8 h~9 h时,系统波动较大、且电网日前电价较高,此时通过备用容量平衡负荷需求。其余时段主要依靠燃气轮机、备用容量和电池充、放电来平衡系统内电负荷需求。从图5可知,在分时电价机制下,蓄电池在2 h~4 h、23 h~24 h谷时电价和15 h~17 h平时电价时段储存电能,在8 h、9 h、18 h和20 h峰时时段售出,实现削峰填谷。

图4 多区域IES电功率优化结果Fig.4 Multi-district IES electric power optimization results

图5 储能充/放电功率优化结果Fig.5 Charge/discharge power of energy storage
3.2 模型经济性分析
由表1可知,经典两阶段鲁棒优化要寻找最劣场景下系统运行总成本最低,因此日前调度计划要满足不确定因素最大波动时系统的鲁棒性,日前调度计划相对于改进两阶段鲁棒优化来说过于保守,造成日前调度成本高于改进两阶段鲁棒优化方案;在实时运行调整阶段,由预测误差引起调度电量和实时发用电量的差值需在实时市场中进行补偿,而实时市场的购电价格高于日前市场,售电价格低于日前市场[15],对于经典两阶段鲁棒优化来说,保守的调度计划需将多余电量在实时市场中以低价售出,调整成本相对较低,改进两阶段鲁棒优化日前调度计划和备用容量较为灵活,只在8 h、14 h~15 h不确定变量波动较大的时间段在实时市场内购买部分电量,造成实时运行调整成本略高,但该方案系统运行总成本较低。因此,改进两阶段鲁棒优化得到的调度计划具备更强的鲁棒性和抵御实时市场电价波动风险的能力。
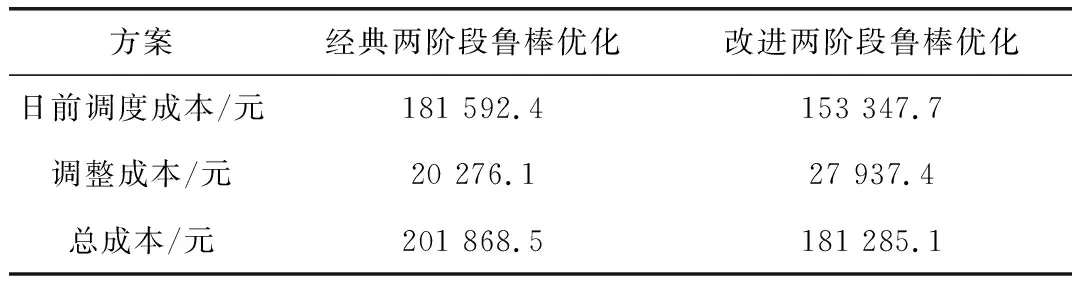
表1 不同优化方案下系统运行成本Tab.1 System operating costs under different optimization schemes
表2为不同预测误差(光伏出力/电负荷预测误差)下系统运行成本对比。随着预测误差的降低,不确定变量的波动区间缩小,两种鲁棒优化的日前调度计划与实时运行下系统发用电量的偏差值不断降低,日前调度成本和实时运行下调整成本都快速下降,且经典两阶段鲁棒优化运行总成本下降较快。当预测误差较低时(如5/5%),两种鲁棒优化方案的日前调度成本相差不大,但改进两阶段鲁棒优化需在实时市场中以高价购入部分电能,使其调整成本较高,造成运行总成本高于经典两阶段鲁棒优化运行总成本。因此,改进两阶段鲁棒优化在预测精度略低的系统中经济性更好

表2 不同预测误差下系统运行成本对比Tab.2 Comparison of system operating costs under different prediction errors
4 结术语
基于改进两阶段鲁棒优化方法建立了考虑可再生能源和负荷波动的多区域综合能源系统经济调度模型,分析结果表明:
(1)采用CCG算法求解提出的改进鲁棒优化模型,得到期望场景下最优,任意场景下可行的系统运行成本最小的调度方案。通过对比分析两种鲁棒优化方法,验证了改进两阶段鲁棒优化得到的调度方案具备更强的鲁棒性和抵御实时市场电价波动风险的能力;
(2)改进两阶段鲁棒优化方法对于经典两阶段方法的优势随着预测误差增大而显著增加,提出模型有利于调度人员在运行成本和风险之间进行合理选择。

