变PWM步长的爬山法在光伏发电系统中的应用*
裴贝贝,王维庆,王海云,李媛
(新疆大学 电气工程学院, 乌鲁木齐 830047)
0 引 言
在追求低碳社会的今天,太阳能作为一种清洁的可再生能源,越来越受到各国的重视。然而,目前光伏电池的太阳能转化率较低,因为光伏电池易受内部环境和外部环境如温度、辐照度和负载等因素的影响,使得输出功率也在不断变化。因此实现最大功率点跟踪在光伏系统的控制中尤为重要[1-7]。
目前,国内外已经有很多学者对最大功率点跟踪(Maximum Power Point Tracking,MPPT)算法进行了研究。文献[7]在梯度式变步长扰动观察法基础上加入了功率预测算法,确保前后2次扰动的判断是在同一功率曲线上进行,消除了误判现象;文献[8]将恒压法与一类改进型扰动观察法相结合,并引入模糊PID控制,该算法以稳压为主,控流为辅,有效避免了母线电压“崩溃”现象,该算法适合单级式光伏系统;文献[9]提出了固定电压法结合扰动观察法的MPPT算法,克服了固定电压法跟踪效率不高、扰动观察法在最大功率点附近振荡工作造成一部分功率损失的缺点;文献[10]针对单相两级光伏并网系统,提出了一种结合固定电压法与增量电导法的占空比扰动的MPPT算法,结果证明该方法在提高功率追踪速度、降低功率扰动的基础上能够保证追踪的准确性;文献[11]提出了一种由扰动观察法、二次插值法和恒定电压法的控制方法,该方法解决了简单拟合的二次曲线跟实际的P-U曲线很难吻合并造成功率损失的问题。文献[12]提出了过山车法,利用PIC16F877单片机构建了最小系统控制的Buck电路,很好地解决了跟踪振荡的问题,该算法适用的主要范围是负载端的阻抗比光伏电池最大功率点(Maximum Power Point ,MPP)处的等效阻抗小的情况。
以上文献大多根据功率测量来确定扰动方向和步长,通过改变功率转换器的工作点,确保系统能够以尽可能小的振荡和误判来追踪MPP,但并没有对MPPT系统的效率进行综合评估。采用可变PWM步长的爬山法,在外部环境或者负载突变的情况下,通过单次迭代确定扰动方向和扰动量的大小,研究了传统爬山法和可变步长爬山法在最大功率点跟踪过程中的响应时间、恢复时间和系统的效率。在 Matlab/Simullink 平台上搭建了模型,并构建了光伏模拟器,通过仿真和实验验证了该方法对提高系统效率的优越性。
1 光伏阵列的特性
通常光伏模块由若干个串联或并联的光伏电池组成。当光子照射时,光伏电池产生直流电能。图1显示了基于单二极管模型设计的PV模块的等效电路图。
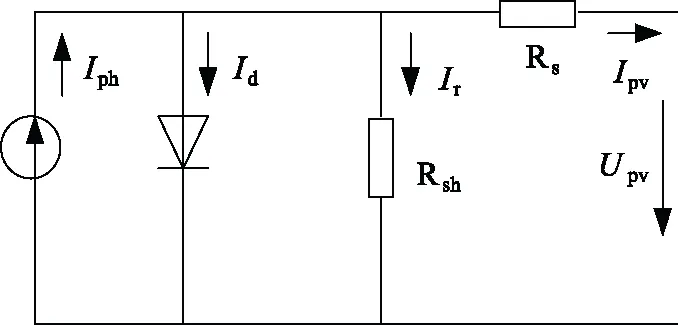
图1 光伏电池等效电路图Fig.1 Equivalent circuit diagram of photovoltaic cell
(1)
式中Upv表示输出电压;Iph为光生电流,该量受太阳辐照度和温度的影响;Id为二极管饱和电流;Rs为串联电阻;Rsh为分流电阻;q为电子的电荷;n为二极管排放系数;k为波尔兹曼常数;T为电池温度。Id与T有关,Iph与光照强度S和T均有关。一般在正常工作的情况下,随辐照度的变化,光伏电池U-I和P-U特性曲线分别如图2(a)和图2(b)所示。
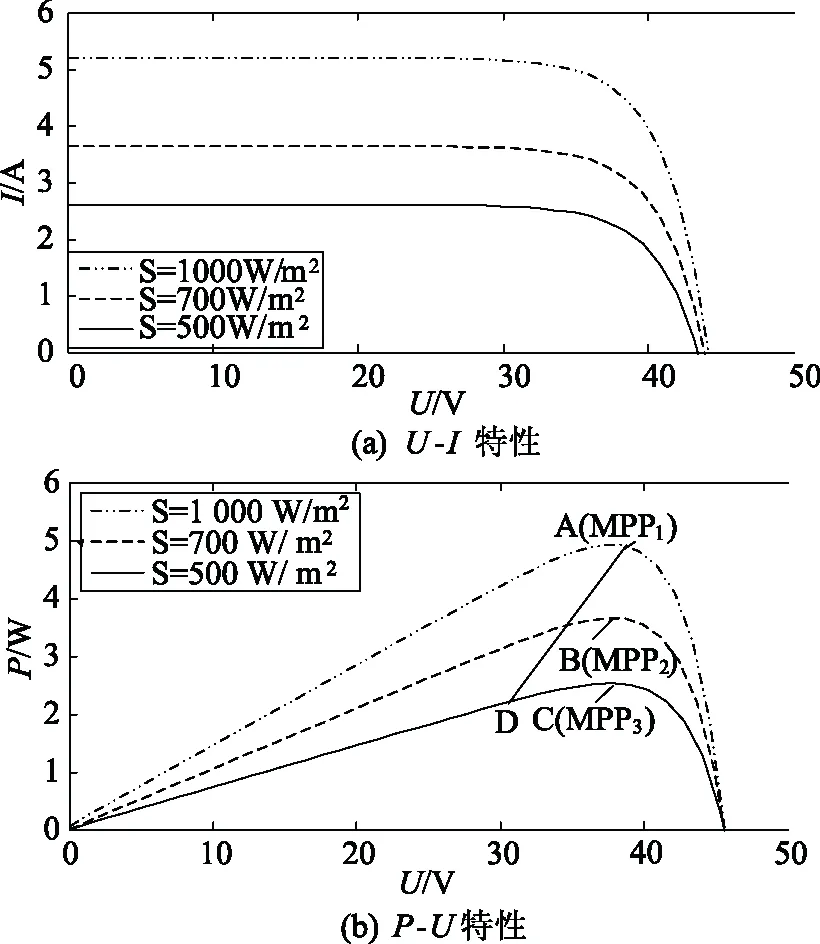
图2 相同温度而不同辐照度条件下光伏电池的特性Fig.2 Characteristics of photovoltaic cells with the same temperature and different irradiance
2 爬山法MPPT控制
当一个直流线性负载连接到一个光伏阵列时,由于光伏阵列典型的非线性特征,工作点不太可能是MPP。这一特性清楚地显示在图2中,每一个辐照度水平只有一个最佳点存在。因此,为了在不同的负载和天气条件下定位MPP,需要一个跟踪系统。可以通过使用DC/DC功率变换器来连续调节光伏阵列电压来跟踪MPP。在大多数应用中,MPPT转换器使用直流开关模式来充电。为了调节光伏阵列电压,必须改变DC/DC变换器的占空比。光伏阵列输入电压、输出电压和占空比(D)之间的关系由以下等式控制:
Upv=UO(1-D)
(2)
改变占空比,它实际上改变了开关的持续时间。占空比必须迭代更新,直到根据下面的等式获得理想值:
D(n+1)=D(n)+ΔD
(3)
式中ΔD是占空比的扰动量,ΔD的大小会影响整个系统的效率,算法的成功运行必须谨慎选择此参数。为了更快的响应MPPT系统,ΔD需要选取较大的值,尤其是在天气变化快的情况下。一方面,在稳定的天气条件下,随着工作点在MPP附近的振荡,较大的ΔD值将会使效率降低。同样,较小的ΔD值将会使MPPT系统的效率达到峰值,也就是说,工作点尽可能接近MPP。
爬山法是基于开关型DC/DC变换器的光伏阵列功率与占空比的算法。当MPPT控制器中ΔP/ΔD=0,实现局部最大功率点。判据如下:
(4)
通过扰动功率变换器的占空比,观察光伏电池的电流和电压的变化,对ΔP/ΔD进行评估,然后运行MPPT控制器,然而,MPPT扰动观察法的循环会使电压和电流产生波动。图3为基于爬山法的流程图。

图3 传统的爬山法Fig.3 Traditional climbing hill method
图2(b)描绘了不同辐照度下的P-U特性曲线。如图,假设MPPT系统在点A处位于MPP,那么跟踪系统将在这一点附近保持振荡,直到运行条件发生变化。当辐照度从1 000 W/m2下降到500 W/m2,导致运行点从A移到D,而D点不是这个光照级别的MPP,从而触发跟踪系统将工作点的MPP移到点C。因此,为了达到这个电压值,必须通过降低占空比来增加,如式(2)所示。MPPT系统达到MPP的效率是受从D点移动到C点所需时间的高度影响,这依赖ΔD选取的大小和实际扰动需要。
在大多数的最大功率点跟踪算法中,扰动量ΔD通常是固定的。ΔD的大小会影响整体MPPT效率,影响响应时间与功率振荡。为了解决这些问题,必须有一个可变步长的MPPT系统,它能够区分动态和稳态。

3 可变PWM步长的爬山算法
与上面描述的可变步长算法不同的是本文提出的方法不依赖查找表格或多个固定步长,而是在单次迭代中确定扰动方向和扰动量ΔD的大小。参照图4,改进的方法旨在减少在最大功率点处 ΔD=0时的功率差,ΔP=Pn-Pn-1。等式ΔD=ΔP×M用来权衡动态和稳态的变化,其中M是缩放因子,例如,如果M=1,Pn= 8、Pn-1= 4、ΔD= 4,是一个正扰动,步长值为4%。如果Pn= 3、Pn-1= 8,ΔD=-5,是一个负扰动,步长值为5%,其在相反方向跟踪。如果Pn和Pn-1相同,这使得ΔD= 0,工作点位于MPP,MPPT系统将停止运行。
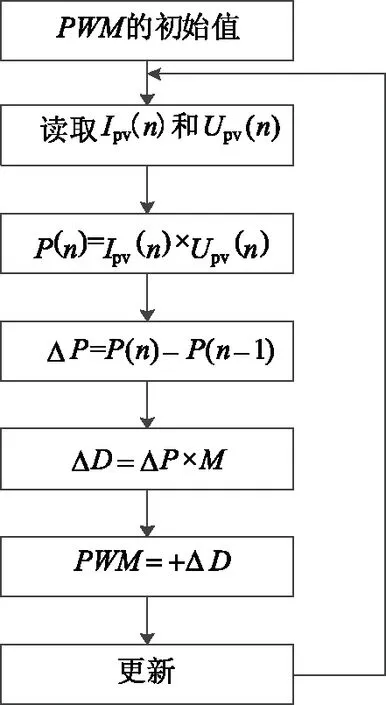
图4 改进的爬山法Fig.4 Improved hill climbing method
4仿真结果与分析
为了验证所提算法的实际效果,比较修改后的变步长法与传统固定步长法的性能,搭建了基于太阳能电池等效电路的Matlab/Simulink模型。仿真是在相同的条件下进行的,包括环境温度、辐照度和采样率。MPPT算法中每秒钟采样8个数据,选择1 000 M/m2、700 M/m2、500 M/m2三个辐照度去模拟稳态和动态条件,如图5所示。环境温度是25 ℃,选取九个步长ΔD值(0.3%、0.6%、1%、1.36%、1.8%、2.5%、3.4%、4.2%、5%)。

图5 固定和可变步长稳态仿真结果显示Fig.5 Steady-state simulation results showing
图5描绘了两个不同的固定步长ΔD(2.5%和5%)和文中提出的可变步长,在1 000 M/m2辐照度下的占空比曲线和功率曲线。
图6显示固定ΔD0.3%在不同辐照度阶跃变化条件下的MPPT系统输出性能,每次辐照度变化时,系统定位MPP所需的时间称为瞬态响应时间(ts),从辐照度变化到恢复稳定所需的时间称为恢复时间(tr)。在这个实验中,辐照度在1 000 M/m2、700 M/m2、500 M/m2之间不断变化。从图中可以观察到,当辐射度发生突变时,MPPT系统需要很长时间才能恢复到MPP,从而导致MPPT系统整体效率降低。为了提高效率,尽可能的通过优化ΔD来使响应时间和恢复时间最小化。
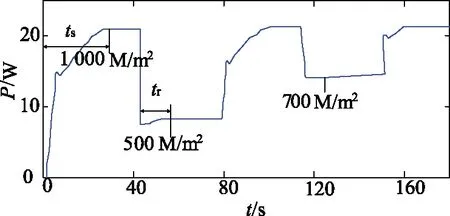
图6 固定步长动态条件下的最大功率点跟踪系统特性Fig.6 MPPT system with fixed ΔD performance under dynamic condition
MPPT系统可变步长的输出特性如图7所示,响应时间和恢复时间都很小。为了减少振荡,该算法自动调整ΔD的大小,在动态的情况下采取比较大的值,在稳态条件下,采取比较小的值。

图7 可变步长动态条件下的最大功率点跟踪系统特性Fig.7 MPPT system with variable ΔD performance under dynamic conditions
为达到更好的效率,采用动态和稳态两方面对MPPT系统的性能进行综合评估。最大功率点的跟踪效率为:
(5)
其中,最大功率点的实际值是指:在最大功率点跟踪系统受到扰动的情况下,采样若干数据,所得出的功率值。

表1 固定ΔD和可变ΔD 最大功率点跟踪系统的效率Tab.1 MPPT system efficiency using variable ΔD and range of fixed ΔD
表1说明了采用变ΔD和固定ΔD的动态和稳态条件下的MPPT系统效率。利用方程(5)计算效率。从表中可以看出,变步长爬山法在动态和稳态条件下都取得了较好的效果。
5 实验台验证与分析
检验基于爬山法的MPPT控制策略的效率和平均功率,如图8,检验装置由一个通过升压转换器给负载供电的PV模拟器组成。一个基本的光伏模拟器由一个可控的电流源组成,通过调整电源的电流控制来模拟不同的辐射度。

图8 MPPT光伏系统Fig.8 MPPT PV system
直流升压系统的规格如下:输入电容Ci为420 μF,升压电感L为60 μH,输出电容Co为220 μF,开关频率f为32.12 kHz。
图9描述了固定和可变ΔD在MPPT系统稳态条件下的实验结果。固定步长选择了2.5%和5%,从图中可以很明显看出,较小的ΔD,振荡的振幅在MPP附近减小;对于较大的ΔD,产生的振荡较大,反而导致效率较低。当工作点位于MPP时,占空比没有变化,所提出的变步长爬山法没有出现振荡的迹象。

图9 PV模拟器实验结果Fig.9 Experimental result obtained by using PV emulator in lab showing
在实际操作中,随着辐照度水平的迅速变化,动态条件很可能发生变化。
当辐射水平从1 000 M/m2突然下降到500 M/m2时,MPPT系统的响应如图10所示。固定步长MPPT系统,ΔD采用0.3%和1.36%两个值。从图10(a)可以看出,恢复时间为6 s。增加步长到1.36 %,恢复时间降低到1.2 s。为满足动态条件,在MPPT系统中自动调节可变步长ΔD,可使ΔD=15%,因此,占空比从35%下降到20%。一旦满足动态条件,MPPT系统自动调节可变步长ΔD,使ΔD在稳态条件下尽可能最小化。

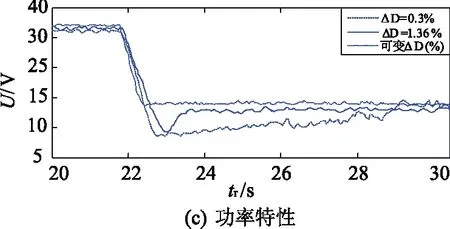
图10 辐射度突然下降MPPT系统恢复时间Fig.10 Recovery time of MPPT system in response to a suddenly drop in a irradiance level
当辐照度从500 M/m2突然上升到1 000 M/m2,固定步长MPPT系统以占空比的增加使工作点运行到最大功率点,如图11(b)显示。以固定的步长0.3%定位到新的MPP的恢复时间为4 s,而固定步长1.36%所用的恢复时间下降到1 s。因此,为适应动态环境,该占空比从20%增加到30%。

图11 辐射度突然上升的MPPT系统的瞬态响应时间Fig.11 Transient response time of MPPT system in response to a suddenly increase in a irradiance level
采用动态和稳态两方面对MPPT系统的性能进行综合评估。

表2 固定ΔD和可变ΔD MPPT系统的效率Tab.2 MPPT system efficiency using variable ΔD and range of fixed ΔD
表2列表得出,文章所提的可变步长算法优于固定步长的算法。
6 结束语
提出了一种可变步长的爬山算法,当外部环境或者负载突变时,能够快速的对光伏最大功率点跟踪系统做出响应,改进了响应时间ts、恢复时间tr和功率振荡,同时节省了追踪时间,提高了追踪精度,提升了转换效率。通过仿真平台和实验台两方面对所提算法进行了研究。结果表明,可变步长的爬山算法相对固定步长的爬山法的具有显著的优越性,尤其是在天气不断变化的条件下,因为它能在动态或稳态的条件下灵活的采用不同的步长ΔD来响应运行条件,使之达到最佳状态。

