基于k中心点聚类的稳态电能质量预警阈值研究
刘建华,刘艳梅,冯纯纯,李锦程,张屹修
(中国矿业大学 电气与动力工程学院, 江苏 徐州 221008)
0 引 言
随着我国智能电网产业结构的升级,无论配电还是发电环节都在向自动化方向发展,在自动化实现的过程中,电力系统应用到了大量的非线性电力电子元件,同时直流输电技术和FACTS技术也广泛应用于实际工程中,这些都会给电力系统带来谐波和电压波动等影响,降低了电网的电能质量[1]。这些也会对电能的生产、传输、分配和使用带来影响,甚至引发严重的电力事故,造成巨大的经济损失。因此对电能质量进行预警显得尤为重要,对降低电力事故、提高电力企业的市场竞争力和满足用户的供电要求也具有重要的意义。
在电能质量研究方面,目前主要集中在电能质量监测系统,扰动源识别、分类,信号去噪,治理技术等方面[2-6],而电能质量预警阈值方面的研究很少,文献[7]提出了基于模糊聚类算法的阈值设定方法,此方法在建立模糊相似矩阵的基础上构造动态聚类图对电能质量数据进行分类,虽然此方法可以达到阈值选取的目的,但模糊矩阵及动态聚类图的的建立过程繁琐,算法复杂,文献[8]将图像灰度分割领域的知识运用到电能质量预警阈值分割,应用Otsu算法,根据类间方差最大和类内方差最小的特性将电能质量数据进行二分化即分为正常和异常类,在此基础上确定客观阈值。虽然文献[8]比文献[7]算法更容易实现且能够取得很好的效果,但文献[8]涉及的电能质量数据过于理想化,实际数据的偏峰度值并不符合文献[8]所述情况,这容易导致分类的误差,当异常和正常类之间的偏峰度值差别不明显时,使用文献[8]的方法有可能导致错误的结果,同时文献[8]的方法需要遍历所有可能分类的均值和方差,计算量大,分类时间长。
文中提出将k中心聚类的方法应用到数据的二分化当中,只需要取k=2就可以把数据分为正常和异常类,该方法能够有效地逼近真实的分类模型,基于此方法确定的客观阈值与文献[8]中所提方法相比较,该方法效果理想且能提高计算效率,算例结果表明所提方法的有效性。
1 数据预处理和k中心点聚类算法
1.1 电能质量数据预处理
从电能质量监测平台所得数据需经预处理之后再运用k中心点聚类算法,此时得到的预警阈值较准确且能够减少算法的复杂度,数据预处理的步骤包含以下几步:
(1)稳态电能质量预警指标的选取参考文献[10]进行,对得到的电能质量数据判断其完整度,如果数据不完整,要填补缺失数据,一般以前后数据的平均值代替,数据完整的前提下利用小波变换法对数据去噪声处理,最后对数据归一化处理;
(2)计算一定窗口内电能质量数据集合的特征量,包含最大值、最小值、平均值、标准差、偏度,峰度、偏峰度乘积;
(3)利用公式(1)计算两两基本样本之间的欧氏距离,设置一定的差异度限值,不超过限值的样本归为一类,将基本样本集合分为L类,数据经预处理后的方便后续的分析计算。
(1)
式中pj、oij表示集合p、oi的第j个特征量;m是特征量个数。
1.2 k-medoids聚类算法
k-medoids聚类算法是一种把实际数据集合中的k个对象作为中心点或中心对象进行划分的k中心点聚类算法,其分类的方法是,给定数据集合V={p1,p2,…,pL},L是待分类的数据集合个数,pi={pi1,pi2,…,pim},m是数据集合pi的特征值个数,以任意的k个数据集合作为初始聚类中心,以其余对象到所选中心对象的距离作为聚类相异程度的度量[9],其定义为:
(2)
式中disp(p,oi)是对象p、oi之间的欧氏距离;ci是第i个分类集合;oi是ci的中心;k表示将所有数据分为k个集合,具体分类步骤为:
(1)从数据集合V中任k个对象作为初始聚类中心点(o1,o2,…,ok);
(2)计算剩余其余L-k个对象到各中心点的欧氏距离,计算公式为式(1),比较各欧氏距离的大小把剩余L-k个对象指派给离对象最近的中心点所代表的集合,所有对象分配完毕,计算Eabs;


(5)重复步骤(3)~步骤(4),直到所得相异程度值最小为止结束。
2 基于k-medoids聚类的阈值算法
2.1 基于k-medoids聚类的阈值算法
设置电能质量预警阈值的目标是将监测得到的电能质量数据进行分离,由于监测数据中正常和异常两类数据间特征值差别较大,而同一类数据的特征值都在一定小范围之内波动,电能质量监测数据的这种良好的聚类特性特别符合k-medoids聚类算法的要求,因此提出了基于k-medoids聚类的阈值算法。
k-medoids聚类算法中的k值选取是一个值得谨慎考虑的问题,在实际应用中k值的选取常常需要根据智能算法或专业知识确定,在电能质量预警阈值选取的问题上,k被取值为2正好达到分割的目的。
利用k中心点聚类算法,将通过电能质量监测平台得到的N个数据分成两类,即:正常和异常类。将分类的质量度量函数定义为:
F=min(Eabs)
(3)
(4)
式(4)是分类的绝对误差,ci为正常类或异常类,oi是ci的中心点。欧氏距离的计算采用公式(1)。由定义可知,当Eabs越小时越符合实际分类模型。
基于k中心点聚类的阈值确定算法具体过程为:在数据预处理已经被分为L类的前提下,随机选择两类数据作为分类的初始中心,对于其余的L-2类数据使用公式(1)分别计算其到两个中心的距离,依据距离中心点的远近,把L-2类数据分到离其最近的中心点所在的集合中,这样所有数据被分为两类,然后使用公式(4)计算本次划分的绝对误差Eabs。上述过程迭代进行,每次迭代总是选择能使绝对误差变小的聚类划分结果,直到绝对误差值不能再小为止[11-12]。
采用基于k中心点聚类的分类算法迭代结束后,都能够找出数据分类的一个合理阈值点。该算法的迭代次数因初始中心点的选择而不同,初始值选择的与理想值接近,则较少的迭代次数就能获得较理想的分割效果,但如果初始值与理想值相差较远,则迭代次数比较大,最坏情况下需要遍历所有的组合情况,文中的L类数据最多迭代L*L次才能找到最佳阈值分割点。为了能够使数据分类效果达到最佳,可以增大算法的迭代次数,但这就会增加计算的时间。针对该算法本身固有的缺陷,将该算法进行优化改进,提出了更适合电能质量阈值确定的k中心点聚类快速阈值算法。
2.2 基于k-medoids聚类的快速阈值算法
k-medoids聚类的快速阈值算法基于这样一个假设:具有所有数据最大值的一类数据始终属于异常类数据的中心。从实验数据来看,该假设对于绝大部分的电能质量数据都是成立的。该算法考虑了数据分布密度,最多迭代L次就够找出最佳阈值分割点,算法的效率和精度相比基于k-medoids聚类的算法得到了极大的提升,解决了算法时间运行时间长的问题。基于k-medoids聚类的快速阈值分割算法的具体过程为:首先在1~L类数据之间统计出所有数据最大值所在的那一类数据记为o1,然后依次遍历1~L类之间的每一类数据记为oi,在迭代过程中,依据距离中心点o1和oi的远近将其他数据分别聚类到o1和oi所代表的集合中,计算每次划分的绝对误差Eabs,最后选取具有最小绝对误差的那次划分结果作为最后的结果[13]。
从以上内容可以看出,基于k-medoids聚类的快速阈值分割算法确定最终客观阈值时仍要计算各初始类之间的欧氏距离,数据预处理时各窗口已经根据特征值大致分类,数据的属性在分类过程中已经固定,同时考虑到最终选取的客观阈值是正常类数据的最大值,因此进行二分化聚类计算时只需要选择最大值来计算各类数据的欧氏距离和分类的绝对误差,该算法的步骤如下:
(1)将电能质量数据中最大值所在的类作为一个固定的中心点,令o1=max(pi);o2=0,此时绝对误差为正无穷大记为E0;
(2)从 1~L类选择一类作为正常类中心点,即:o2=pi;i=1,2,…,L;选择好中心点之后,计算其余类pj到两个中心点的距离,(j=1,2,…L)&(i≠j);
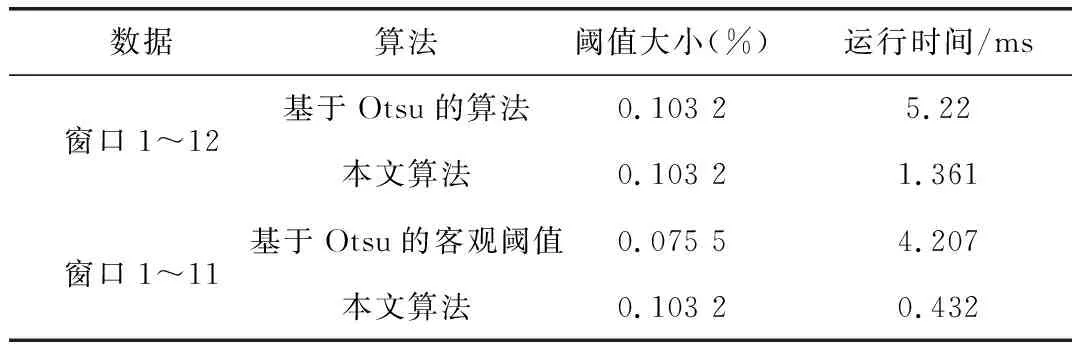
(3)若满足 dist(pj,o1) (4)若满足Eabs (5)选择具有最小误差的分类结果作为最终结果,同时选择正常类的最大值作为电能质量的客观阈值。 采用对某焦化厂连续六小时监测得到的负序电压不平衡度为例,数据如图1所示,简述了稳态电能质量预警阈值算法的有效性,并与文献[8]的分割效果进行对比。 图1 电能质量原始数据Fig.1 Original data of power quality 预处理:本例中共有120个数据,数据连续完整,以每个窗口10个数据进行划分得到12个窗口数据,计算每个窗口的特征值,采用公式(1)进行处理初始聚类分析,可得结果如表1所示。 表1 初始聚类结果Tab.1 Initial results of cluster 采用文中的快速阈值分割方法,以第8类数据的最大值作为异常类的中心o1,不同的o2时对应的绝对误差为表2所示。 表2 不同分类中心对应的分类结果和绝对误差Tab.2 Classification results and absolute errors corresponding to different classification centers 由表2可以看出,当以第8类数据作为异常类中心,以第5类作为正常类中心时分类的绝对误差最小,选择此分类作为最终数据二分化分类的结果,最终,选择前五类中最大值作为客观阈值,即t0=0.103 2 %。 采用文献[8]方法,所得结果和文中分割结果相同,但采用基于Otsu的客观阈值算法,需计算不同分类时的数据均值和方差,只要计算不同分类中心时最值之间的绝对误差即可,提高了计算效率。把文中的方法和基于Otsu的客观阈值算法进行比较,其结果如表3所示。 表3 2种方法的阈值和运行时间比较Tab.3 Comparison of threshold and running time of 2 methods 上述正常和异常数据之间偏峰度差别较大,有较好的分割效果,但当二者之间差别较小时,采用文献[8]方法有可能出现误差。仅取上例中部分数据(前110个)为例,采用文中方法和基于Otsu方法的阈值选取结果如表3所示。 实验结果表明,基于Otsu的阈值分割算法对两类偏峰度差别较大的数据来说有较好的分类结果,但如果异常数据的偏峰度值较小则基于Otsu的算法会使原有数据的有效信息丧失,基于k心点聚类的阈值分割算法不考虑正常和异常类的距离,其分割效果优于Otsu算法,但k中心点聚类算法在阈值分割时效率不尽人意,而改进的快速k中心点聚类算法则保证了分割效果,也将效率提高到比Otsu算法更高的水平。 在客观阈值的基础上,可综合考虑专家意见给出的主观阈值[8],结合客观阈值,利用比例加权的方法得到更加合理的预警阈值,最终计算公式为式(5),以图1数据为例,得到最终阈值为t=0.089 5 %。 t=a*t0+(1-a)*t1 (5) 式中t0是客观阈值;t1是主观阈值,本例中t1取0.08%。 通过k中心点聚类的快速阈值算法得到电能质量数据的客观预警阈值,是阈值选取中最为重要的一步,最终通过综合专家意见结合比例加权法得到最终阈值,所得阈值符合实际,克服了以往单一且存在一定主观性的专家赋值的弊端,是电能质量预警平台的建立的基础,提出的是一种快速有效的阈值分割算法,以某一焦化厂的实测数据为例验证了所提方法。最后,因电能质量异常数据形式多样,在接下来的研究中考虑对该方法进行优化,使其更好的适用于电能质量预警平台的建立。3 案例分析



4 结束语

