基于出口选择概率的修正社会力模型的行人疏散研究

霍富昌，姜志侠，谢继轩，张时赫，薛天坤

（长春理工大学 理学院，长春 130022）

社会力模型是一种应用广泛、仿真效果最接近实际情况的行人运动模型。社会力模型可以对行人在实际疏散过程中表现出来的模式和行为进行仿真模拟[1-3]。大量学者对社会力模型进行研究，陈涛等为解决原有社会力模型中存在的速度振荡问题，引进相对速度对原始模型进行优化[4]。汪蕾等引进了相对速度，并引入恐慌因子对行人的期望速度进行修正，得到了社会力修正模型，在一定程度上，能够较好的仿真突发事件下的行人疏散运动[5]。

虽然社会力模型有着众多的优点，但其也存在一定的局限性。尤其是在行人疏散过程中，原始模型没有有效的机制来防止行人重叠现象，而且当行人密度较大或较小时，会发生一些不符合实际的现象。

基于原始社会力模型，引入紧张因子、相对速度以及出口吸引力对社会力模型进行修正，然后借鉴元胞自动机模型，建立防重叠机制并确立相应的出口选择机制，最后建立多出口行人疏散综合模型，对多出口场所内的行人疏散行为进行仿真模拟。

1 模型

1.1 原始社会力模型

Helbing的社会力模型基于牛顿第二定律，行人i所受合外力fi（社会力）是由行人自身驱动力、行人与行人间的相互作用力f、人与障碍物ij间的作用力fiω三个力联合产生，由此建立物理方程[6]：

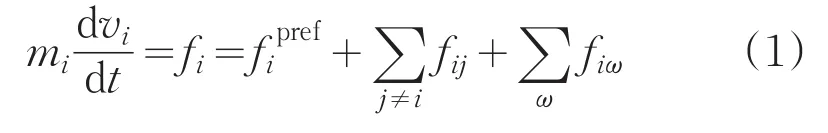
式中，mi代表行人i的质量，vi代表行人的实际速度。

（1）行人自身驱动力

行人自身驱动力是指行人i在期望时间τi内以实际速度vi向期望速度前进，具体物理方程为：

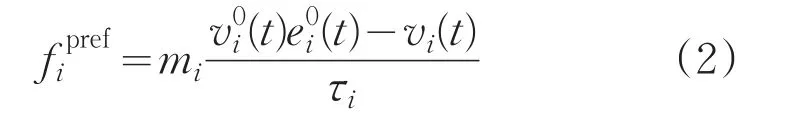
（2）行人与行人间的相互作用力

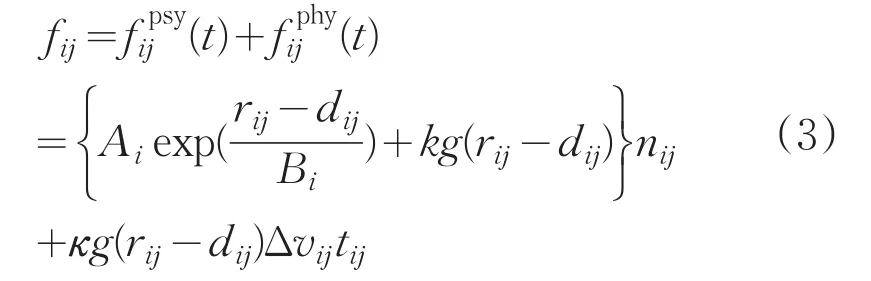
式中，Ai、Bi、k、κ为常量参数，rij=ri+rj代表行人i和行人j的半径之和，代表行人i和行人j质心间的距离，代表由行人j到行i的单位向量，切向向量从而，g(x)是一个分段函数，具体函数如下：

（3）人与障碍物间的作用力

与行人间的作用力类似，人与障碍物间的作用力fiω可表示为：

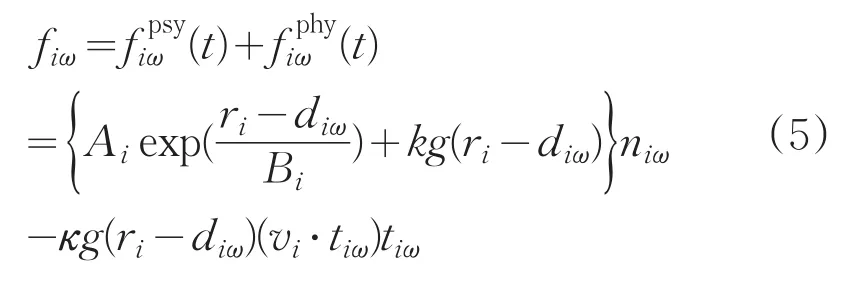
同样，对于墙或障碍物而言，diω代表行人i的质心到障碍物表面的距离，代表障碍物指向行人i的单位向量，切向向量。

1.2 修正社会力模型

针对社会力模型中存在的问题，以及结合现实行人疏散行为，对社会力模型做出一些修正。

（1）期望速度修正

在实际的疏散场景中，行人的期望速度往往不是一成不变的，Helbing加入紧张因子ni(t)来对期望速度进行修正，行人的期望速度可修正为[3]：

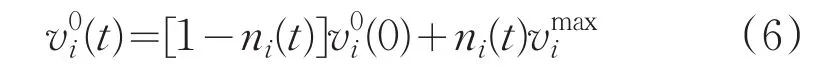
（2）相对速度修正

基于陈涛对相对速度的分析，结合Helbing的社会力模型，考虑相对速度对行人疏散过程中的心理作用力的影响，则社会力原模型中行人与行人间的相互作用力fij及行人与障碍物之间的相互作用力fiω分别可修正为[3]：

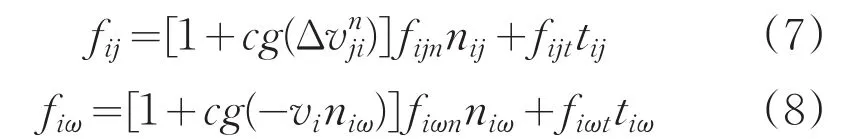
式中，fijn和fiωn称为法向社会心理距离作用力，称为法向社会心理速度作用力。表示疏散人员i和疏散人员j的法向速率差。为相对速度影响系数，代表速度力与距离力的比例关系。

（3）引入出口吸引力

Lakoba认为出口会对行人产生吸引力fik，其具体表达式为[7]：

式中：k代表出口，Ci为常数。

类似相对速度优化中相对速度的影响，在此定义门的相对速度影响系数Ck，其中因门无法移动，只有人员i会移动，从而简写为。同时结合原模型fik可得优化公式：

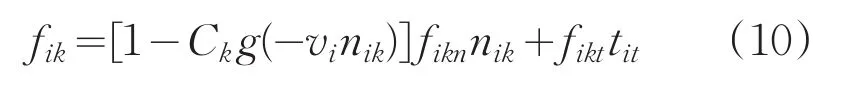
社会力模型修正为：

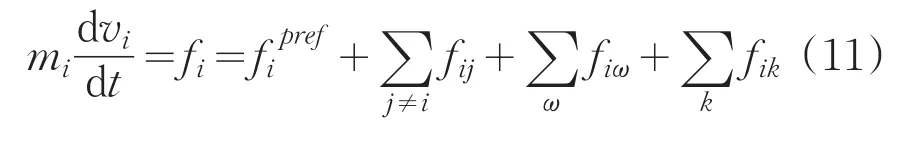
2 出口选择

在对社会力模型的研究中发现，社会力模型在仿真过程中会出现行人重叠现象，因此参考元胞自动机模型将场所化为网格，规定一个行人只能占据一个网格，且行人不能直接越过网格，以来建立简单的防重叠机制[8-11]。

为了解决出口利用不均匀的问题，通过考虑行人与出口的距离以及出口处行人密度对出口选择的影响，基于概率决策，参照文献[12]和[13]，引入出口选择函数：

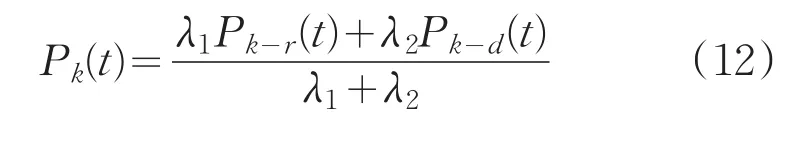
式中，

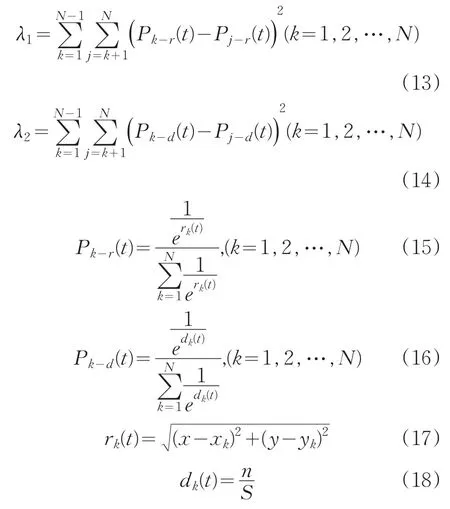
式中，Pk(t)为t时刻选择出口k的概率，λ1是距离指数，即概率Pk-r(t)占Pk(t)所对应的比重，λ2是密度指数，即概率Pk-d(t)占概率Pk(t)所对应的比重，Pk-r(t)是只考虑行人距离时行人在t时刻选择出口k的概率，Pk-d(t)是只考虑行人在出口区域的人员密度时行人在t时刻选择出口k的概率，rk(t)是行人距离出口的距离，dk(t)是出口区域处的人员密度，N是出口总数。

3 构建多出口行人疏散模型

基于修正后的社会力模型，结合出口选择机制，构建多出口行人疏散优化模型，具体模型如下：社会力模型即公式（11）中各修正项由公式（2）、公式（6）、公式（7）、公式（8）和公式（10）构成。出口选择函数是由公式（12）、公式（13）、公式（14）、公式（15）、公式（16）、公式（17）和公式（18）构成。

当某时刻行人与出口的距离相等且各出口区域处人员密度也相等时，则有：

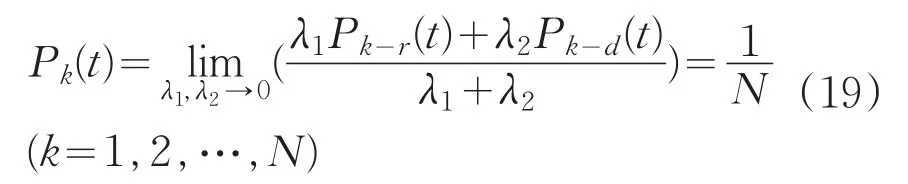
此时行人选择各出口的概率均相等。此时判定选择的出口，以行人i建立坐标系，比较各出口对于行人i位置的方向m与社会力方向fi的夹角θ大小，夹角最小的即为所选择的出口。

出口选择函数对出口引力进行比重均衡，比较概率，最可能选择出口与行人行进方向是否一致，即朝向出口的Pk(t)最大为不改变出口选择。若行人改变出口则不考虑此出口引力，将剩余出口引力均衡计算，重新模拟该时段；若不改变，则按原步骤继续进行，继续下一个时段模拟，以此循环，直至行人通过出口结束。模型模拟流程图如图1所示。

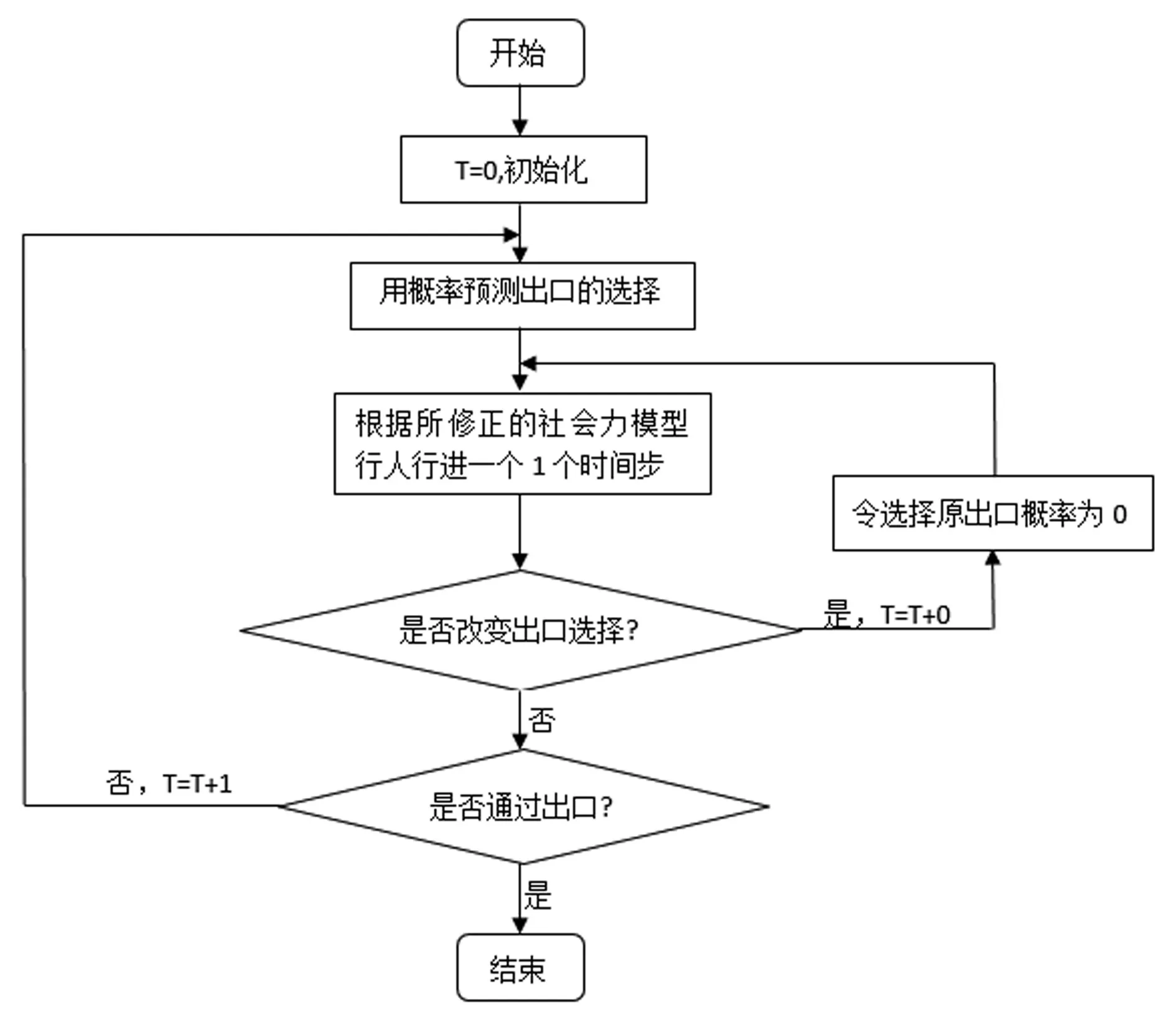
图1 行人模拟过程流程图

4 模型应用分析

4.1 仿真模拟

为了验证提出的基于出口选择概率的修正社会力模型的科学性和可用性，进一步通过仿真模拟来进行模型应用分析。选取15m×15m的房间为疏散环境，假设该房间内有两个出口A、B，两个出口规格相同。设置初始疏散人员为100人，随机分布在房间内，初始分布如图2所示。

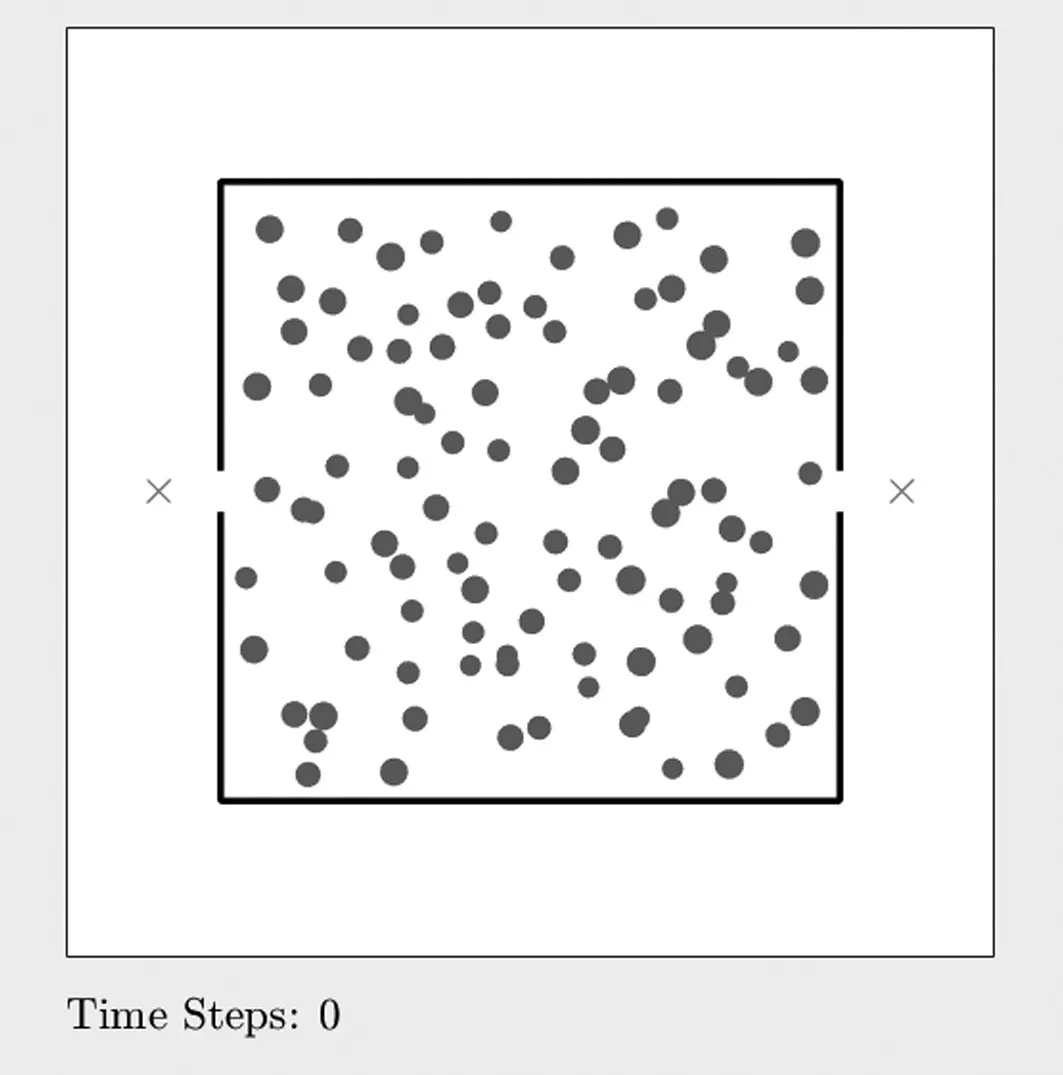
图2 行人疏散模拟初始分布示意图

在疏散开始阶段，行人选择出口时主要是根据到出口的距离，并且在一段时间内更换出口的可能性较小，从而会出现行人呈半圆形聚集在出口位置，行人大致会分为泾渭分明的两部分，如图3所示。然而随着疏散进行等到大量行人聚集在出口位置时，距离因素已不是行人选择出口的主要因素，出口处行人密度成为选择出口的主要因素，部分行人将会放弃距离最短的出口而选择出口处行人较少的出口进行疏散，这与现实生活中的行人疏散情景相符合。

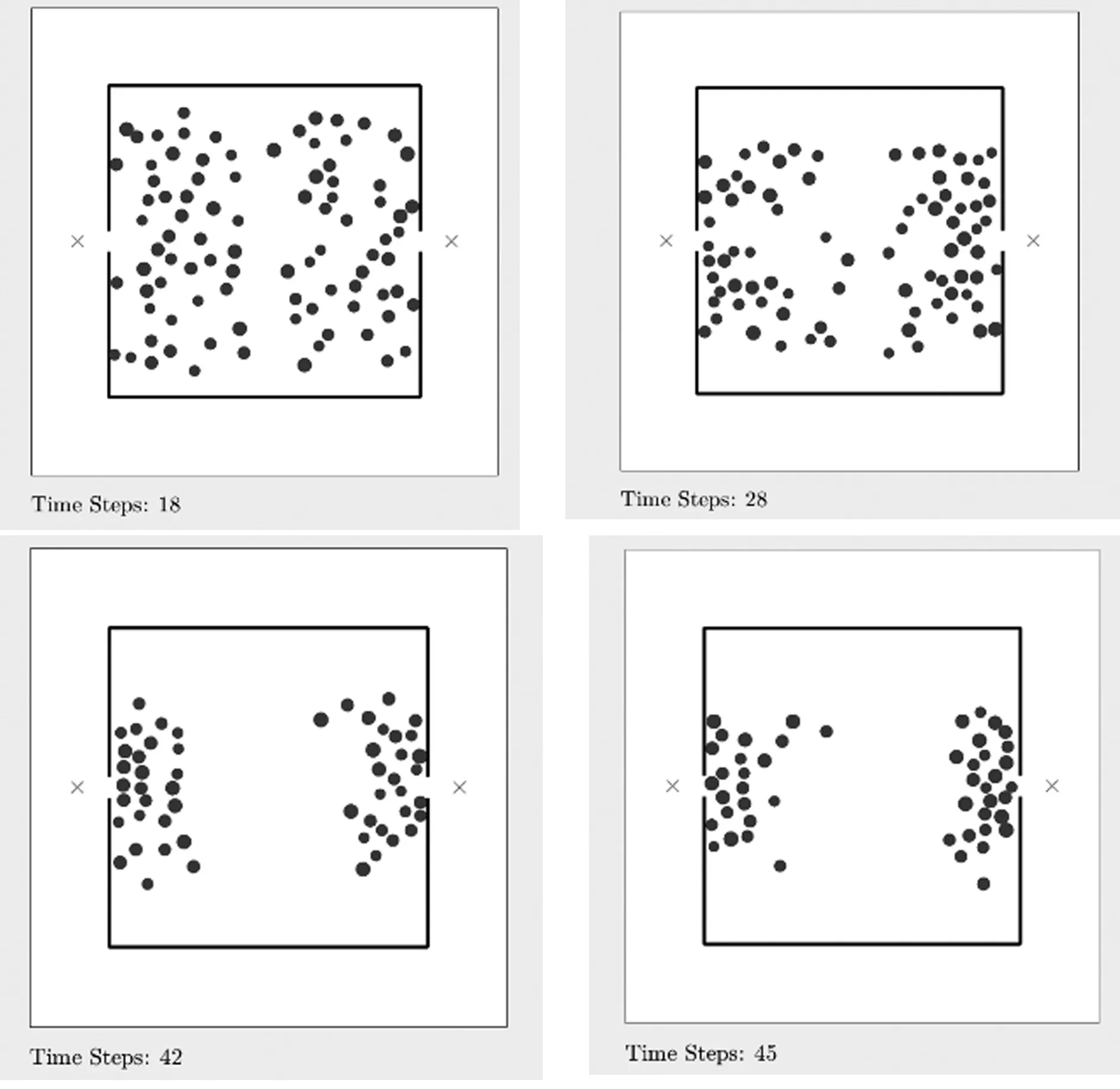
图3 行人疏散过程示意图

4.2 讨论分析

对多出口综合模型进行讨论分析，对比三种模型的疏散效果，即方案1（不使用社会力只基于概率决策的出口选择的理想模型）和方案2（不使用出口选择函数只使用修正后社会力模型）进行仿真模拟（具体方案如表1所示），得到结果如表1所示。

表1 不同的出口选择方案中各出口承担的疏散人数（人）

表1表示行人选择不同疏散方案时的各出口承担的疏散人数。对比图表发现，方案1中，是纯理想化状态，行人不受外界其他因素影响，只考虑距离和行人密度，因此各出口承担的疏散人数相等。但在现实情境中行人的疏散却是受到多方因素的影响，各出口承担的疏散人数明显不相等。方案3中各出口承担的疏散人数趋于相等，这是优化后的综合模型，这与实际相符，说明优化模型和算法的正确性。

为了验证模型的有效性，分别选取疏散场景为15m×15m（场景1）、15m×30m（场景2）、30m×30m（场景3），对这三种场景下的行人疏散进行研究。

统计在不同疏散场景种不同模型的疏散时间，用来分析三种模型所得的出口优化方案对疏散效率的影响，得到了三种模型下的行人疏散的总时间，结果如下表所示。

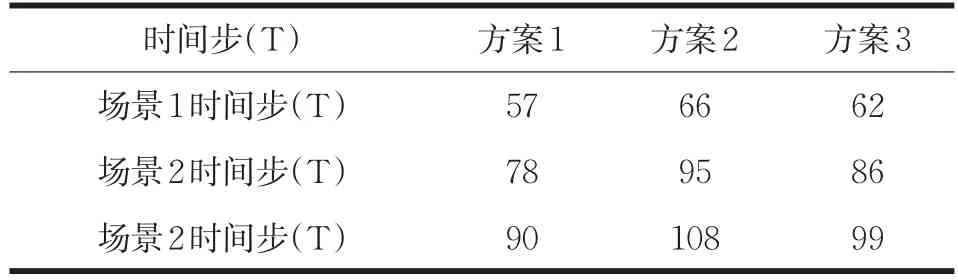
表2 不同模型不同场景下行人疏散总时间

由表2可知：在不同的疏散场景中，方案1是最为理想的状态，时间最短，但这种状态在现实情景中不可能出现；方案2行人疏散所花费时间最长，疏散效果最差；方案3时间趋近于方案1，比较合理，接近理想化疏散。

行人在实际的疏散过程中选择出口是受多种因素的影响，往往由于出口处行人过多导致疏散效率过低。在模型中加入基于概率决策的出口选择函数，实质是考虑行人与出口的距离以及出口处行人的密度对行人出口选择的影响。在行人进行出口选择时，行人将会综合考虑行人与出口距离及出口处行人密度等因素，选择一个对行人自己相对有利的出口进行疏散，从而达到一个比较理想的效果。模拟结果显示：引进基于概率决策的出口选择函数更能真实反映多出口选择下行人的疏散行为。

5 结语

基于实际情形以及社会力模型的复杂性，本文引进相对速度和出口吸引力以及对期望速度加以限制来对社会力模型进行修正，并且建立了简单的防重叠机制，引进基于概率决策的出口选择函数，构建了基于出口选择概率的修正社会力模型，对行人疏散问题进行研究。通过进行仿真模拟，构建的多出口行人疏散综合模型能够较好的反映现实场景中的行人疏散行为，与实际行人疏散行为相符合。因此，该模型具有重要的意义和参考价值。