基于平面波解构的三维体曲率计算方法

李海山,杨午阳

(1.中国石油天然气股份有限公司勘探开发研究院西北分院,甘肃兰州730020;2.CNPC油藏描述重点实验室,甘肃兰州730020)

表示地层弯曲程度的曲率属性通常被用于构造解释和储层分析,因其对各种复杂断层、裂缝、河道及构造弯曲的刻画能力优于相干属性[1],近年来得到了广泛的关注。曲率属性自20世纪90年代中期被引入地震解释,最初采用层面计算方式得到层位曲率[2]。ROBERTS[3]给出了详细的层位曲率计算方法,明确了曲率属性的物理意义并对其进行了系统分类。但层位曲率没有直接利用地震资料的振幅信息,层位解释的质量对计算结果有着严重影响,容易产生构造假象[4],同时也不能实现对整个构造体及构造内部细节的精细刻画[5]。

为克服层位曲率的局限性,AL-DOSSARY等[6]在ROBERTS[3]研究的基础上,提出了三维多谱体曲率计算方法。由于体曲率利用了地震数据体的振幅信息,而振幅信息与构造和岩性变化密切相关,且计算不受人为因素的干扰,因此体曲率属性相对于层面曲率属性表现出诸多的优点[4],很快得到了推广应用[7-11]。解释人员可以从沿层曲率属性上识别出小的扰曲、褶皱、凸起、差异压实特征,而这些在常规解释时无法追踪,在相干上也呈现为连续的高相干特征[12]。体曲率的计算关键在于倾角数据体的计算,目前有多种倾角数据体的计算方法,主要有局部倾斜叠加法[13]、复数道分析法[14]、相干倾角扫描法[15-16]、梯度结构张量算法[17]以及平面波解构法(PWD)[18]等。

平面波解构法最初由CLAERBOUT[19]于1992年提出,其主要思想来源于描述地震数据的局部平面波模型,目前已经广泛应用于波场分离与成像[20]、局部斜率或倾角计算[21-22]、构造导向滤波[23]、反演参数建模[24]、地层自动拾取与拉平[25]等。考虑到平面波解构法具有简单快速、计算精度高、稳定可靠等优点,本文将其引入三维体曲率计算。首先利用平面波解构法将三维地震数据体转化为视倾角数据体,再利用视倾角数据体计算三维空间中任意点的曲率,从而获得三维体曲率属性,最后将该方法用于实际资料的体曲率属性的计算,结果表明本文方法有效且可靠,三维体曲率属性能够精细刻画裂缝发育带和河道等地质特征。

1 方法原理

1.1 基于PWD的倾角体计算

平面波解构滤波器是一种时空域预测误差滤波器,它通过相邻地震道预测当前地震道来估算同相轴局部斜率,其预测准则是原始地震道与预测出的地震道间的残差能量最小。

1.1.1 平面波解构

局部平面波微分方程可表示为[18]:

(1)

式中:u=u(t,x)为波场;t和x分别为时间和距离;σ=σ(t,x)为同相轴局部斜率。

FOMEL[18]在Z变换域中给出了求解公式(1)的隐式有限差分公式:

(2)

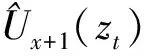
(3)

式中:滤波器B(zt)的系数可以通过在零频率附近进行泰勒级数展开确定,计算中通常采用三点中心滤波器B3(zt)[18]:

(4)

式中:

(5)

1.1.2 局部倾角估算

用C(σ)表示平面波解构算子C(zt,zx)在时间域与地震数据u(t,x)进行二维褶积运算的算子,在最小平方意义下,局部斜率σ的估算可转化为求解最小二乘目标函数[18]:

(6)

由公式(5)可知最优化问题(公式(6))是局部斜率σ的非线性优化问题,利用高斯-牛顿法可将最优化问题((6)式)转化为[18]:

(7)

式中:Δσ为斜率增量;σ0为初始斜率;C′(σ)为C(σ)对σ的偏导数。求解公式(7)后,初始斜率σ0通过加上斜率增量Δσ得到更新,然后循环迭代求解公式(7)。该方法需要进行数次非线性迭代获得期望的局部斜率估计,收敛速率依赖于给定的起始斜率值。得到局部斜率σ后,就可以得到相应的局部倾角θ:

(8)

迭代求解公式(7)得到的局部斜率σ随着时间和空间位置的改变而变化,同时避免如相干倾角扫描法那样的局部时空窗模糊效应。为了提高计算结果的连续性以及对噪声的压制能力,在局部斜率更新过程中,可引入预条件算子和正则化方法[20-21]:

(9)

式中:ε为常系数扰动因子;D为正则化算子。

对于三维倾角体计算,首先沿纵测线方向利用公式(9)对每一个剖面u(t,x)进行计算,获得视倾角体px=p(t,x,y),然后沿联络测线方向利用公式(9)对每一个剖面u(t,y)进行计算,获得视倾角体qy=q(t,x,y),本文计算时起始斜率值均置为0。

1.2 体曲率计算

利用平面波解构法获得的倾角数据体,可计算出三维体曲率属性,下面详细介绍各种体曲率的计算方法。

一个反射面可以用二次曲面方程表示为[3]:

S(x,y)=ax2+by2+cxy+dx+ey+f

(10)

该方程中的系数与前文计算的视倾角px和qy具有如下关系[6]:

(11)

其中,算子Dx和Dy分别表示沿着x和y方向一阶导数的数值近似。在获得二次曲面方程系数后,利用下列公式计算曲率属性[6]。

均值曲率为:

(12)

高斯曲率为:

(13)

最大和最小曲率为:

(14)

最正曲率和最负曲率为:

(15)

倾角曲率为:

(16)

走向曲率为:

(17)

2 局部倾角估算方法性能测试

为说明基于PWD的局部倾角估算方法的性能,下面利用Sigmoid模型[18,26]数据进行测试(图1)。图1a所示的Sigmoid模型包括一个褶皱中发育的断层和褶皱被剥蚀后上覆沉积形成的角度不整合面。利用图1b所示的初始倾角(所有样点均为0)进行迭代求解,50次迭代后得到的解构残差和倾角分别如图1c和图1d所示。由图1d可见估算的倾角剖面中,不整合面上覆缓倾角地层的倾斜角度一致,不整合面下伏褶皱的倾角变化与起伏情况一致,褶皱内的断层也得到了清晰的刻画;由图1c可见解构残差非常小,合成沉积模型中的同相轴信息基本被解构出来,进一步验证了倾角估计的准确性。图2给出了平面波解构残差能量随迭代次数的变化曲线,尽管初始倾角为0,解构残差能量仍然随迭代次数的增加而单调递减,可见基于PWD的倾角计算方法比较稳定。

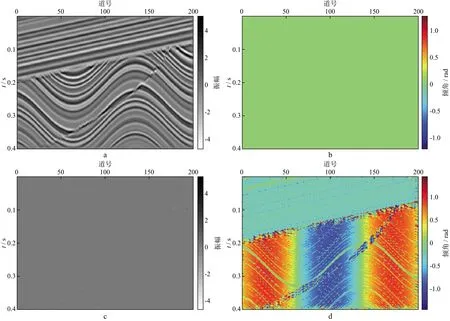
图1 Sigmoid模型及相应的解构残差及倾角剖面(1rad≈57.296°)a Sigmoid模型; b 初始倾角; c 平面波解构残差; d 估算的倾角剖面

为进一步说明基于PWD的局部倾角估算方法计算精度高的优点,将其应用于实际资料的倾角场计算。图3a为某工区叠后地震剖面,图3b为利用平面波解构法得到的相应倾角剖面,图3c为利用相干倾角扫描法得到的相应倾角剖面。由图可见,利用平面波解构法得到的相应倾角剖面对同相轴倾角和断层等不连续性有较好的刻画能力,不仅将如图中红色箭头所指位置处的倾角场进行了准确刻画,而且将如图中黑色箭头所指位置处的断层以倾角场突变的形式也刻画了出来。

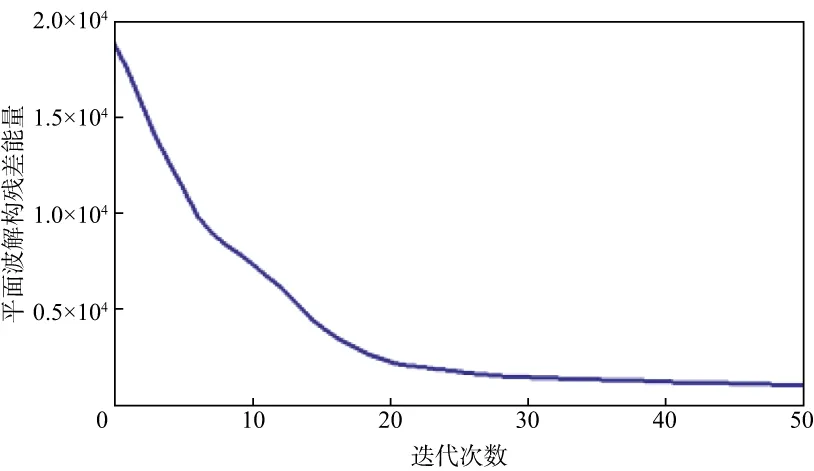
图2 平面波解构残差能量随迭代次数的变化

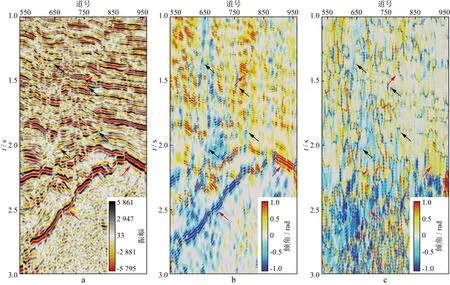
图3 叠后地震剖面及相应的倾角剖面(1rad≈57.296°)a 叠后地震剖面; b 平面波解构法得到的倾角剖面; c 相干倾角扫描法得到的倾角剖面

3 实际资料应用

为验证本文体曲率属性计算方法的有效性,利用西北某油田H工区的地震资料进行了体曲率计算的应用研究。采用的地震资料为三维叠后纵波资料,主要研究目的层为深层裂缝型储层。图4给出了该工区目的层解释层位及沿层振幅切片,图中W1,W2,W3指示了3口开发井位置。图5给出了平面波解构法得到的视倾角沿层切片,为了对比分析,同时采用目前广泛使用的相干倾角扫描法进行了体倾角计算,图6给出了相干倾角扫描法得到的视倾角沿层切片。对比可见平面波解构法得到的视倾角在空间连续性及局部细节的刻画(如图中红色箭头所示的河道及微断裂位置)方面都明显优于相干倾角扫描法得到的视倾角。此外,在同等计算条件下,计算两个视倾角数据体时相干倾角扫描法所用计算时间是平面波解构法所用计算时间的16.51倍,可见平面波解构法的计算效率较高。

图7给出了沿目的层相干切片及利用不同方法计算得到的最负曲率属性切片。图7a为基于本征值结构的相干切片;图7b为利用层位数据计算的最负曲率属性,受层位解释与地震同相轴追踪质量的影响,计算精度和可靠性较低;图7c为利用平面波解构法所得视倾角计算的最负曲率属性;图7d为利用相干倾角扫描法所得视倾角计算的最负曲率属性,在错断等不连续部位,由于在时窗内不能扫描到精确的倾角而导致曲率计算结果模糊。比较可见,图7c的计算精度最高,细节刻画能力优于沿层相干属性,特别是红色箭头所示的河道和微断裂位置及黑色圆圈所示的裂缝发育带位置得到了较细致的刻画。平面波解构法所得三维体曲率属性的计算精度和对地质特征的精细刻画能力在图8给出的沿目的层倾角曲率属性切片上得到了更加突出的体现。

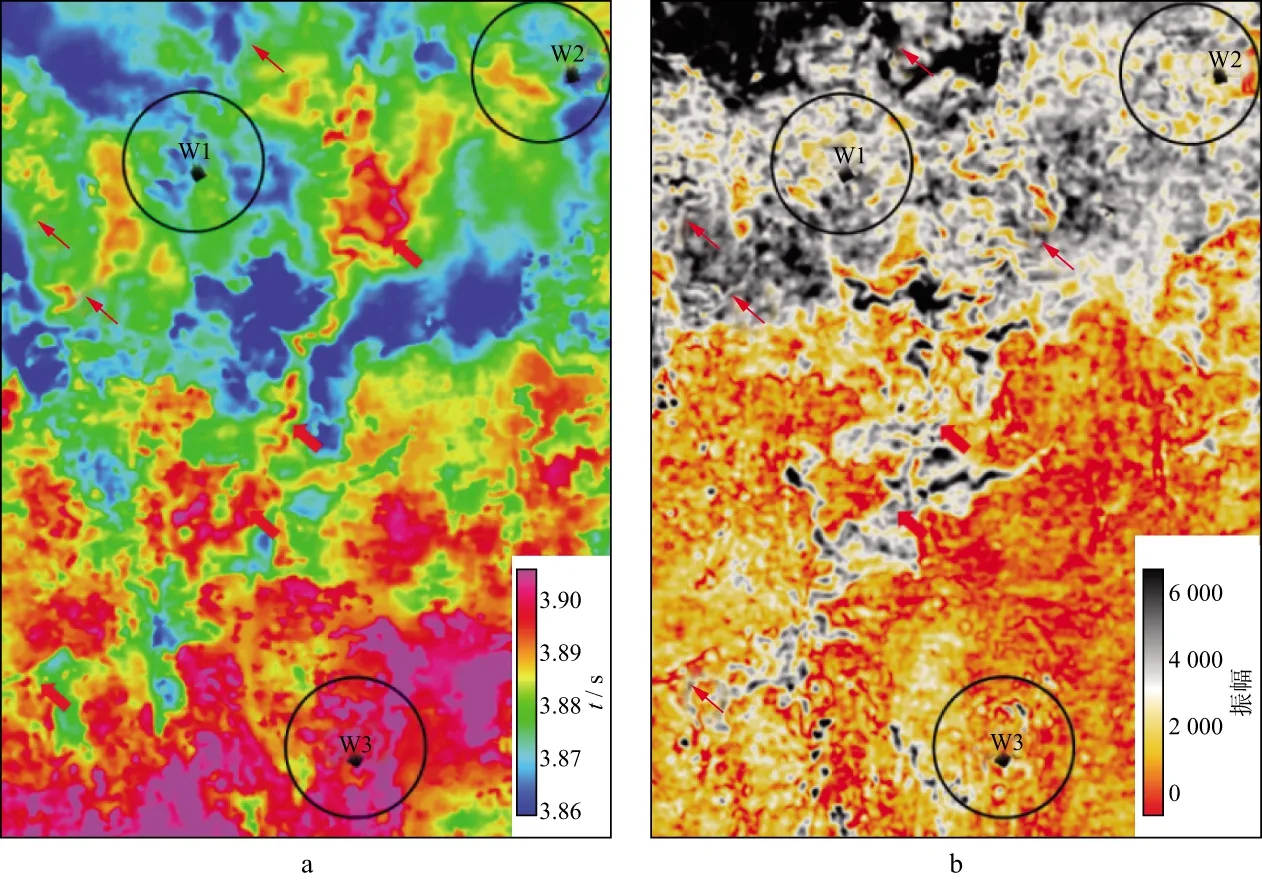
图4 目的层解释层位(a)及沿层振幅切片(b)

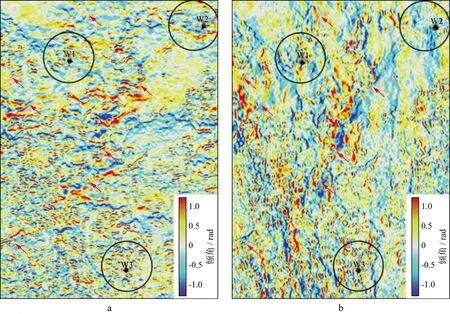
图5 平面波解构法得到的视倾角沿层切片(1rad≈57.296°)a 纵测线方向视倾角沿层切片; b 联络测线方向视倾角沿层切片

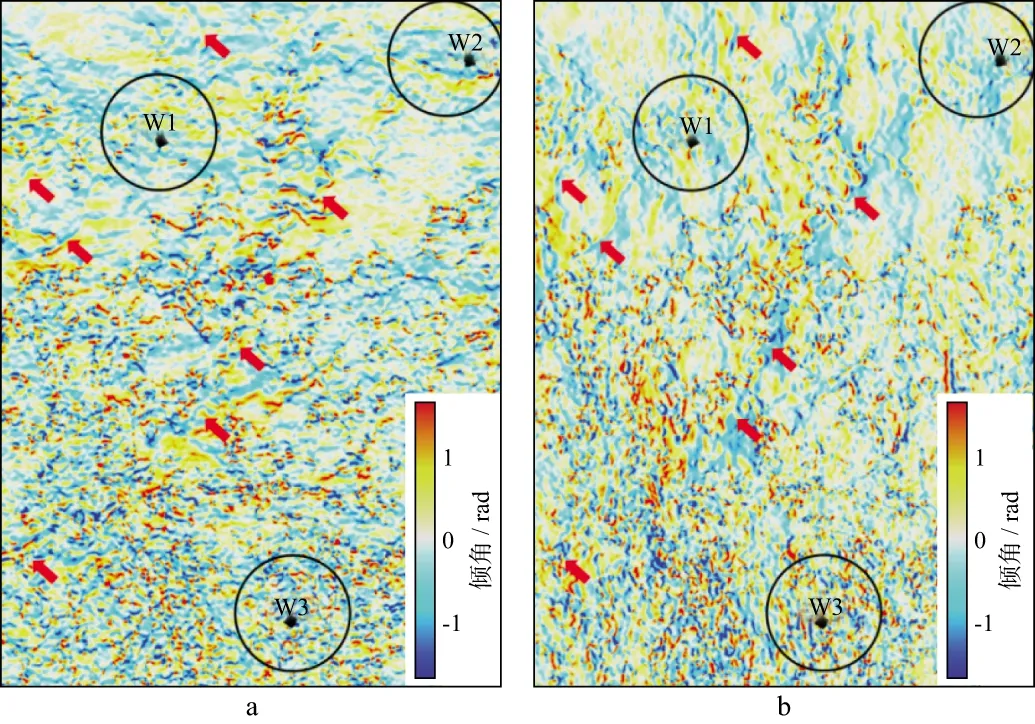
图6 相干倾角扫描法得到的视倾角沿层切片(1rad≈57.296°)a 纵测线方向视倾角沿层切片; b 联络测线方向视倾角沿层切片

图7 沿目的层相干切片及最负曲率属性切片a 基于本征值结构的相干切片; b利用图4a所示解释层位计算的最负曲率属性; c 平面波解构法得到的最负曲率属性; d 相干倾角扫描法得到的最负曲率属性

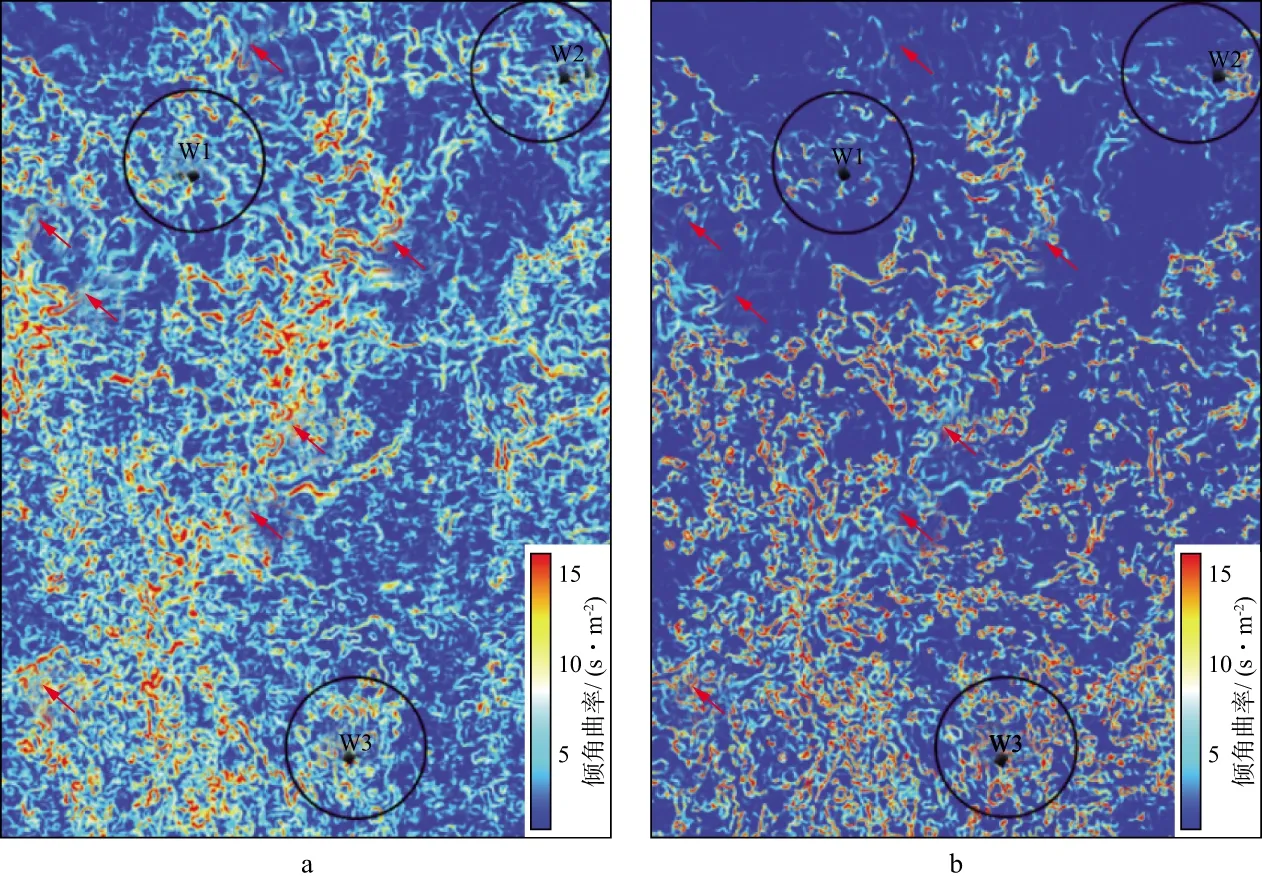
图8 沿目的层倾角曲率属性切片a 平面波解构法得到的倾角曲率属性; b 相干倾角扫描法得到的倾角曲率属性

4 结论

1) 本文方法利用平面波解构法由三维地震数据体计算得到视倾角数据体,再利用视倾角数据体计算三维空间中任意点的曲率,实现基于平面波解构的三维体曲率计算。

2) 本文方法结合了体曲率计算时利用振幅信息、不受人为因素干扰的优点和平面波解构法简单快速、计算精度高、稳定可靠的优点,使得计算效率高、稳定可靠,具有较强的实用性。

3) 实际资料应用结果验证了本文方法的有效性,利用平面波解构法得到的体曲率属性明显优于利用解释层位数据得到的层位曲率属性和利用相干扫描法得到的体曲率属性,对裂缝发育带及河道等非均质地质体有较强的刻画能力。