GWs from S-stars Revolving Around SMBH at Sgr A*∗

Rong-Gen Cai(蔡荣根),Tong-Bo Liu(刘同波),and Shao-Jiang Wang(王少江)

CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China

School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

AbstractA preliminary estimation of gravitational waves(GWs)from the extreme-mass-ratio-inspirals(EMRIs)system in the Galactic Centre(GC)is given for the 37 observed S-stars revolving around the supermassive black hole(SMBH)at Sagittarius(Sgr)A*.Within this century,the total strain of the gravitational waveform calculated from the post-Newtonian(PN)method with eccentricity is well below the current planned sensitivity of pulsar-timing-array(PTA).New technology might be required in order to extract GW signal from this EMRIs system for future PTA detections.

Key words:gravitational waves,extreme-mass-ratio-inspirals,supermassive black hole

1 Introduction

There is a considerable observational evidence for the existence of a supermassive black hole(SMBH)with roughly four million solar masses at Sagittarius(Sgr)A*in the Galactic Centre(GC)(For review,see Ref.[1]),supported by the observed orbits of many S-stars from close monitoring over the past few decades(See Ref.[2],for example).It has been expected in Refs.[3–4]that around 2018 a full data of 16-year-period orbit of the star S2 would reveal much information on relativistic effect.It turns out that,the recent result[5]from the GRAVITY Collaboration has eliminated the pure Newtonian dynamics from S2 data,which has also been used for testing some modified gravity theories in the previous literatures(See Refs.[6–9],for example).Therefore,our Milky Way centre is a valuable play yard for the test of new physics.[10]The current means to explore our GC are electromagneticwave(EMW)observations,for example,the Event Horizon Telescope(EHT)Very Long Baseline Interferometry(VLBI)observations and the infrared interferometry experiment GRAVITY at the Very Large Telescope Interferometer(VLTI)and other experiments like the X-ray observations.

Meanwhile,the coming era of gravitational-wave(GW)astronomy[11−12]provides us a new way approaching the center of Milky Way. A stellar-mass object revolving around a Sgr A*SMBH could be served as an extrememass-ratio-inspirals(EMRIs)system in the GC.[13]Compact object like dwarfs,neutron stars and stellar BHs are not subject to tidal disruption,therefore they can reach very close to the SMBH and thus emit GW signals during the last coalescence phase of merger,[14−18]which can be detected by the future space-borne GW detectors like LISA,[19]Taiji,[20−22]DECIGO,[23]and BBO.[24]Detections of GWs events from such EMRIs system could probe the spacetime metric around the centre SMBH,which gives rise to the independent measurements on the mass and spin.[25]The modified gravity theories can also be constrained by measuring any deviation from Kerr metric through the peribothron as well as Lense-Thirring precession.[26]

However,the current observations on the Sgr A*SMBH also give us many S-stars that are not compact enough to survive the tidal disruption,[27−29]therefore we can only detect such GW signals during current inspiral phase through pulsar-timing-array(PTA)observations,which to our best knowledge has not been specifically discussed in the literatures.Nevertheless,we still point out here some previous literatures addressing similar issues.In Ref.[30],it was claimed by simulatioins that there must be one to a few low-mass main sequence stars sufficiently bound to the Sgr A*SMBH to be conspicuous sources in LISA observations.In Ref.[31],the prospect of detecting GWs background by PTA observations from the intermediate-mass-black-holes(IMBHs)and stellar BHs orbiting around Sgr A*SMBH was estimated,although we have yet no convincing evidence for identifying any of such BHs in GC.In Ref.[32],it was shown that mass leakage occurs through the outer Lagrange point L2 could accelerate the time-evolution of the EMRIs system of a main-sequence star and an SMBH,resulting in a GW signal detectable by future space-borne GW detectors.

The arrangement of this paper is as follows:In Sec.2,the post-Newtonian(PN)method with eccentricity is outlined for binary BHs(BBHs)with arbitrary mass ratio;In Sec.3,the total strain of the gravitational waveforms from 37 observed S-stars is given.Section 4 is devoted to conclusion.For reference,the dataset and gravitational waveforms for each S-star are given in the Appendices A and B,respectively.

2 The GWs from Eccentric BBHs System

The post-Newtonian(PN)approximations are expansions in terms of v/c,where v is velocity of object and c is the speed of light.They are used to find weak field solutions to Einstein’s equations.The expansion coefficient of(v/c)nis called nPN coefficient.The 0PN denotes the Newton’s law of gravity and using the adiabatic approximation,one can obtain the rate of decay of the orbital semimajor-axis and eccentricity.It comes to 1PN,1.5PN,and 2PN when studying the evolution of the orbital elements with the quasi-Keplerian parametrization of the orbit.The conservative 3 PN dynamics might be needed if one wants to construct models beyond the adiabatic approximation.

In this section,we follow closely the paper[33](See also Refs.[34–53]for the 0PN,1PN,1.5PN,2PN,3PN and 3.5PN results)on the eccentric PN model since only the early-stage inspiral phase is considered in our case.In what follows,the 3PN conservative quasi-Keplerian orbit equations are solved with the solutions from the 2PN truncated adiabatic evolution equations of the orbital elements to construct the adiabatic PN waveform to leading Newtonian order.

The system under consideration is made up of two point particles of masses m1and m2.The total mass,the reduced mass and the symmetric mass are denoted as M=m1+m2,µ =m1m2/M,and η = µ/M,respectively.The unit convention is G=c=1.

In Newtonian case,the conservations of energy E and angular momentum J can be expressed in terms of the eccentricity e and mean motion n,which can be related to the orbital period P and the semi-major axis a by n=2π/P=a−3/2M1/2.Then the conservative orbital dynamics of the relative orbital radius r and angular frequency˙ϕ is given by

where the eccentric anomaly u satisfies the Kepler’s equation l=u−esinu with the mean anomaly l given by ˙l=n.For constant n and e,the above conservative orbital dynamics can be solved for the input initial conditions ϕ0≡ ϕ(t0)and l0≡ l(t0).

In the PN case,the quasi-Keplerian parametrization gives rise to three eccentricities,et,er,and eϕsignifying the deviations from circlar motion in t,r,and ϕ.As stated in Ref.[33],it is sufficient to consider just et,or e for short.In Ref.[33],it is also shown that the dubbed x-model can match the numerical relativity much better than the usual n-model.Here x ≡ (Mω)2/3with ω ≡ (2π+∆ϕ)/P,where∆ϕ is the angle of precession of the pericenter during one orbit of period P.

First,one solves the 2PN truncated adiabatic evolution equations of the orbital elements

for the given initial conditions x0≡x(t0)and e0≡e(t0).Here the PN coefficients are given in the appendix of Ref.[33].

Then,one solves the 3PN conservative quasi-Keplerian orbit equations

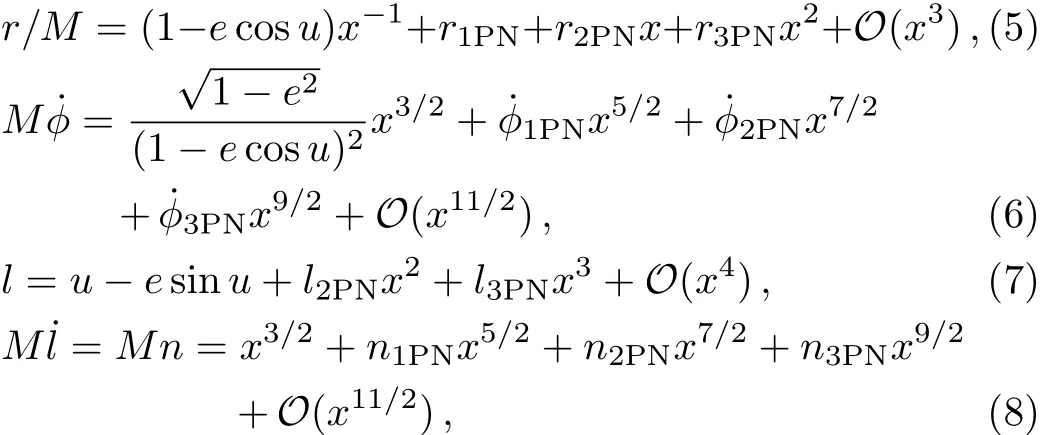
with input time-varying solutions x(t)and e(t).Here the PN coefficients are given in the appendix of Ref.[33].To be more specific,one first integrates Eq.(8)to obtain l(t)with integration constant l0≡l(t0),and then one solves u(t)from Eq.(7)by root- finding with l(t),and next one can compute r(t)directly from Eq.(5),and(t)directly from Eq.(6).At last,the(t)and ϕ(t)can be obtained by numerically differentiating and integrating the r(t)and(t),respectively,with integration constant ϕ0≡ ϕ(t0).

Finally,with the solutions of r(t)and(t)(and also(t),ϕ(t))in hand,one can express the complex PN waveform strain to the leading Newtonian order as

where ϕ′= ϕ − φ,R is the radial distance to the binary,θ and φ are the spherical polar angles of the observer in the orbital plane.

3 The Total GW Strain from 37 S-stars

The mass MSMBH=4.02×106M⊙and distance R=7.86kpc of Sgr A*SMBH are adopted from Ref.[2]The data set of S-stars orbiting around the Sgr A*SMBH is taken from Ref.[54],where the semi-major axis a[arcsec],the numerical eccentricity e,the inclination angle i[degrees],the position angle of the ascending node Ω[degrees],the longitude of periastron ω[degrees],the epoch of periastron passage tP[year]and the K-band apparent magnitude mKare provided as referred here in Table 1.The masses for each S-star are also not specified in Ref.[54],which will be estimated later in the last column of Table 1.

The intial time is chosen at t0=tPso that l0=0 and ϕ0=0.The spherical polar angle θ of the observer in the orbital plane is simply equal to the inclination angle i,which measures the angle between the orbital plane and the plane tangential to the celestial sphere as shown in the upper left part of Fig.1.It is between 0◦and 90◦for counter-clockwise apparent motion,and between 90◦and 180◦for clockwise apparent motion.As explicitly shown in Fig.1,the other spherical polar angle is given by

with the upper sign for counter-clockwise apparent motion,and the lower sign for clockwise apparent motion.This simple relation is limited to the case without the rotation of SMBH[47](See Refs.[14,55]for the general case).We hope to report elsewhere the general case of a spining SMBH.

To estimate the masses for each S-star,one can first combine the definition of bolometric magnitude

with the definition of K-band BC correction

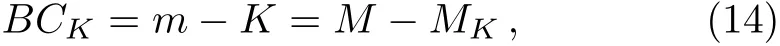
to give rise to

Then one can replace the bolometric magnitude M with K-band apparent magnitude mKby

where the distance could be chosen roughly as D=8kpc and the K-band extinction δK=2.4.Next,one can also replace the BC correction BCKby the semiempirical relation adopted from,[56]

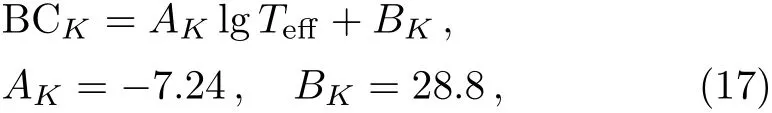
where the effective temperature Teffof star can be estimated by the Stepan’s law L ∝ RT4,namely

Finally,after inserting the semiempirical relations

one eventually obtains

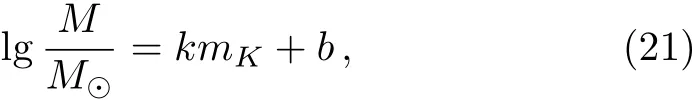
where

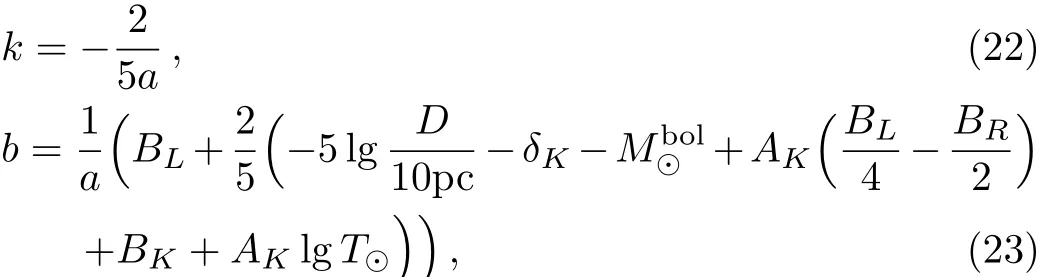
with

The linear coefficients k=−0.192 and b=3.885 can be simply calibrated from a smaller data set[57]by naively fitting the determined masses and K-band magnitudes.Although the mass refereed from the K-band magnitude is generally smaller than the true mass,[57]however,the EMRIs system is actually dominated by the SMBH,whose mass is much larger than the mass of stars.Therefore the precise values in the last column of Table 1 are not important since it makes little difference on the final results of gravitational wavefroms.

Using above data for the 37 observed S-stars orbiting around the Sgr A*SMBH,one can directly calculate the gravitational waveforms for each S-star as presented in appendix A.The GW frequency is at the order of decades,namely nHz band for PTA observations.The total gravitational waveforms for the amplitudes of the two polarizations are presented in Fig.2,where the GW signal is dominated by the S2 star.When the stars approach the periastrons,their velocities tend to reach the maximium values.Therefore the GW amplitude obtains a burst over one orbital period,which can be seen from Fig.2.The dominated one is thus produced by the S2 star as the period is almost 16-years consistent with that of S2 star.However,the total amplitude 10−20–10−19is well below the sensitivity of current planned PTA observations,say 10−15–10−14as reviewed in Ref.[58].

Fig.1(Color online)An illustration of the conventions used in our calculations.The observation frame(red arrow lines)is the usual elliptical coordinate,where the direction of SMBH is along the unit vector n.The source frame(magenta arrow lines)contains two polarization unit vectors p and q in addition to n. p goes through the ascending node,which is the endpoint of the intersection line between the orbit plane and the tangent plane to the elliptical sphere.Two different orbits(cyan ellipse and blue ellipse)are shown with the same orbit angular momentum L labeled by the green arrow line,whose inclination angle from the orbit plane to the tangent plane is labeled by i.The cyan ellipse is speciall since its minor axis is exactly along p,thus the projections of both n and q on the cyan orbit plane exactly go through the periastron.In this case,the angle ω from the ascending node to the periastron is exactly π/2.The blue ellipse with arbitrary angle ω is shown for a general orbit.The direction of observer is specified by the two polar anle θ and φ,which can be determined by θ =i and φ =3π/2 − ω as shown from the illustration.

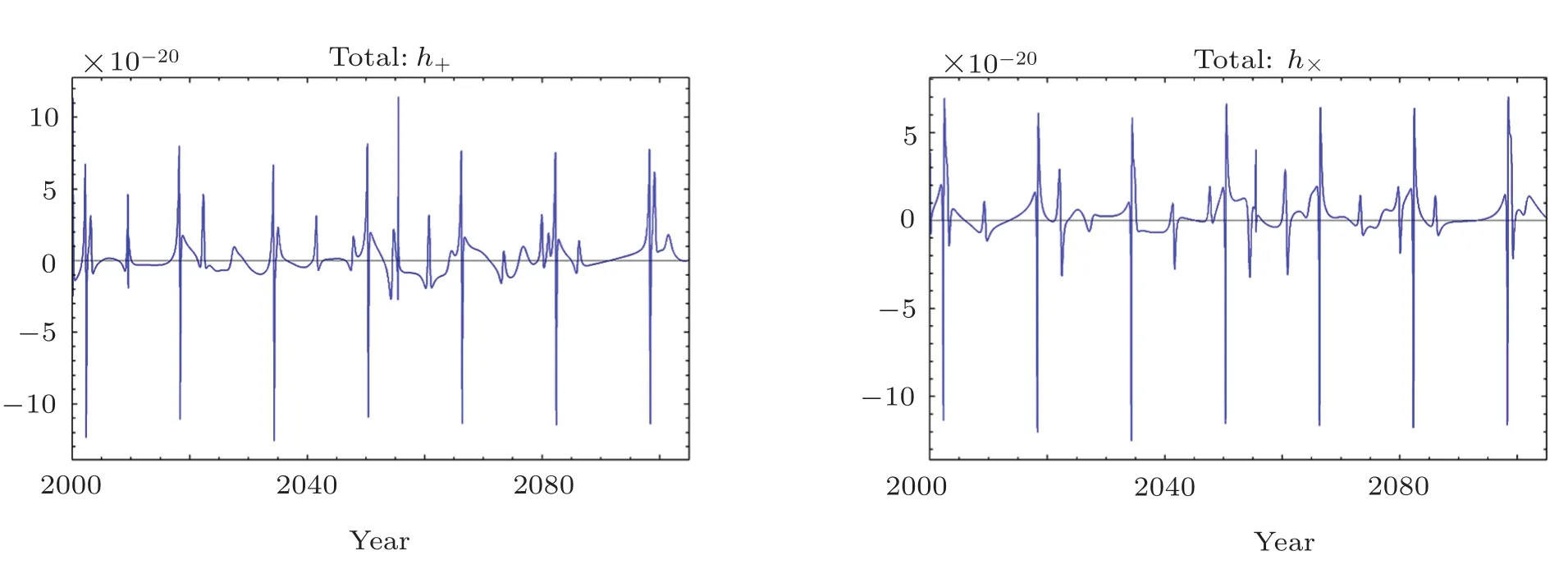
Fig.2 (Color online)The total amplitudes of the two polarizations for 37 observed S-stars orbiting around the Sgr A*SMBH in GC with respect to the observation year within this century.

4 Conclusions

Our GC may be the most important laboratory for testing the EMRIs system against new physics since there are much appealing evidences for the presence of an SMBH at Sgr A*.Previous studies have revealed the exciting possibility to detect the GW signals from the compact objects orbiting around this SMBH within the sensitivity range of future space-borne GW detectors like LISA,Taiji,DECIGO and BBO.In this paper,we explore the possibility that if one can detect the GW signal from the non-compact main sequence stars orbiting around the Sgr A*SMBH.The gravitational waveforms are explicitly calculated from an eccentric PN model for 37 observed S-stars,and the total amplitudes for each polarization are well below the sensitivity of current planned PTA observations,which might require new technology other than extending the observation time in order to extract GW signal from this EMRIs system for future PTA detections.

Appendix A:The Data Set of 37 S-stars

Appendix A is devoted to give a full data set on 37 S-stars that is directly related to our estimation of their gravitational waveform.The aim of this paper is to extract the total gravitational waveform as realistic as possible,hence we include as many S-stars as possible in the literatures with complete orbital data.

Table 1 The dataset of 37 S-stars we used in this paper for estimating the gravitational wavefrom adopted from Ref.[54],where the semi-major axis a[arcsec],the numerical eccentricity e,the inclination angle i[degrees],the position angle of the ascending node Ω [degrees],the longitude of periastron ω [degrees],the epoch of periastron passage tP[year],the K-band apparent magnitude mK,and the star mass mstarreferred from the K-band apparent magnitude are shown below.

Appendix B:The Waveforms of 37 S-stars

Appendix B lists all the gravitational waveform for each S-stars as specified in each panel in Fig.3,where the left column presents the h+strain,and right column presents the h×strain.The horizontal axis presents the observation year,expanding from the year 2000 to the year 2105.Since we are use the adiabatic PN waveform to leading Newtonian order,the total gravitational waveform can be obtained by a direct superposition of each waveform at the same year.

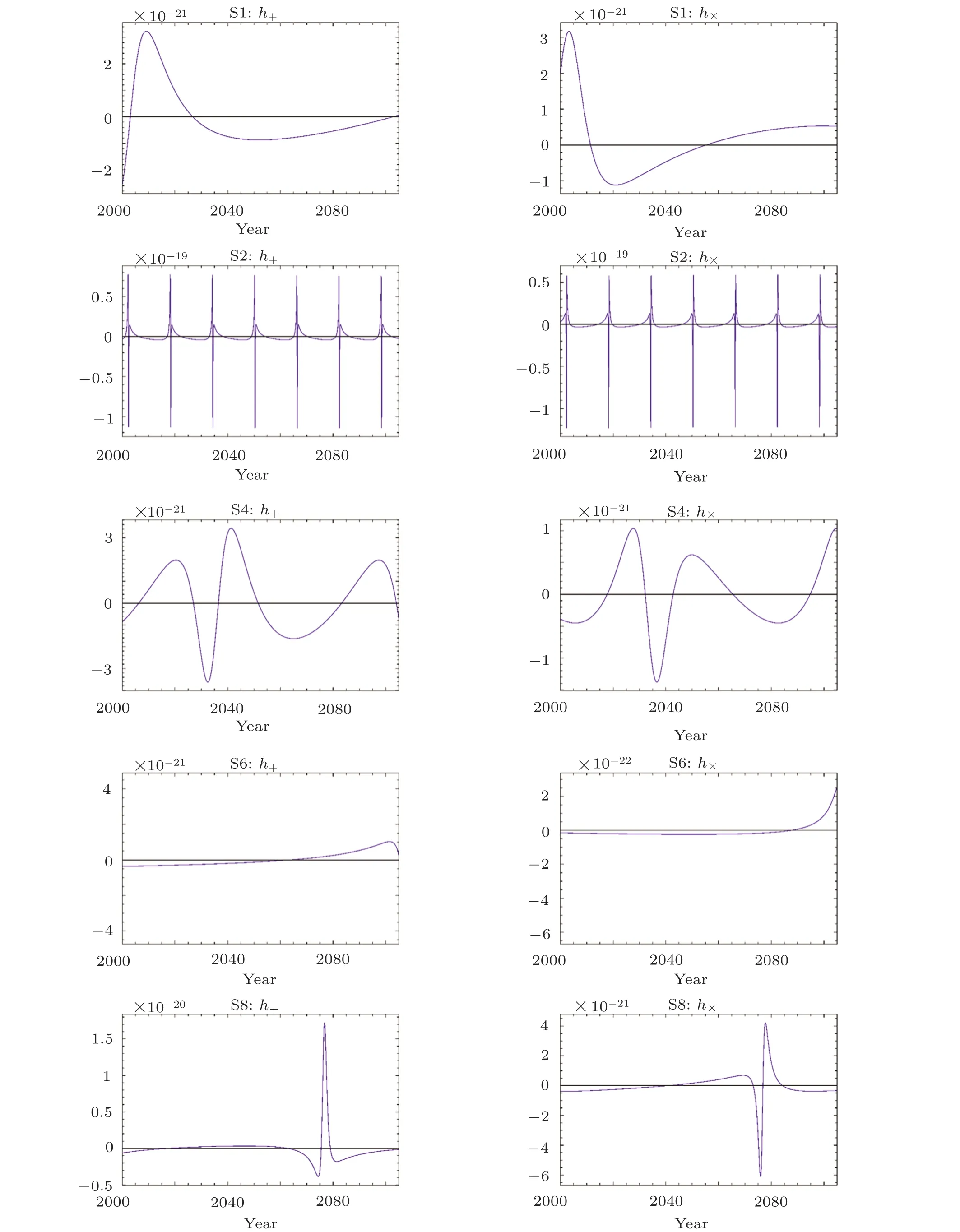
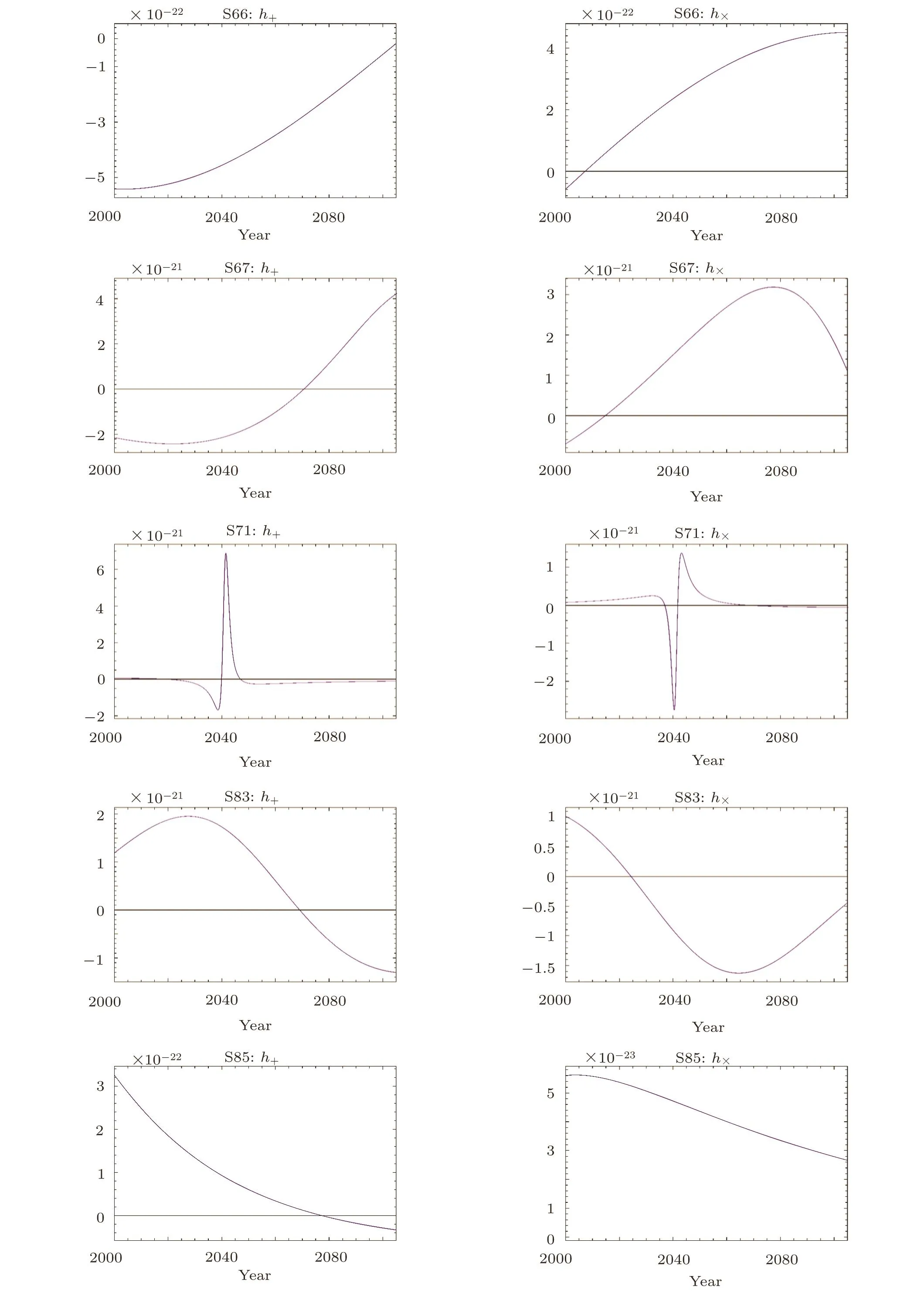
Fig.3 (Color online)The Waveforms of 37 S-stars.

Acknowledgments

We would like to thank Xian Chen,Li-Wei Ji,You-Jun Lu for helpful discussion during the Workshop on Gravitational Wave Physics and Detection at the Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing between 15-28th July,2018.We also want to thank Li-Ming Cao,Wen-Biao Han for helpful discussion and Hu Bin and Qi Guo for helpful correspondences.We also acknowledge the use of HPC Cluster of ITP-CAS.