Collective Di ff usion and Strange-Metal Transport∗

Lin-Peng Du(杜林鹏), Shao-Feng Wu(吴绍锋), and Guo-Hong Yang(杨国宏)

1Department of Physics,Shanghai University,Shanghai 200444,China

2Shanghai Key Lab for Astrophysics,Shanghai 200234,China

AbstractWe study a particular combination of charge and heat currents,which is decoupled with the heat current.The “heat-decoupled” (HD)current can be transported by diffusion at long distances,when the thermoelectric effect is small,large,or balanced.Using holographic models with momentum relaxation,we illustrate that the different thermoelectric effects correspond to the high temperatures and strong disorder,low temperatures,or special critical index.Meanwhile,the Einstein-like relation and the diffusion/chaos relation may be emergent.Assuming that the existence and features of HD modes appear in strange metals,we can predict that when the thermoelectric effect is not very large,the scaling of resistivity is predominantly controlled by the HD susceptibility and chaos;otherwise more physics is required.

Key words:gauge/gravity duality,strange metal,thermoelectric transport

1 Introduction

In condensed matter physics,the ubiquitous appearance of linear in temperature resistivity is very mysterious.Typical materials with such strange-metal hallmark include copper oxides,heavy fermions,organic conductors,vanadium dioxide,ruthenates,fullerenes,and pnitides.Obviously,the underlying dynamics for the transport in strange metals should be independent of the scattering mechanism and interaction details.Moreover,the quasiparticle picture is not applicable because at high temperatures the resistivity can cross over the Mott-Io ff e-Regel(MIR)limit.[1−2]The strange-metal region is shaped like to the quantum critical region of insulators in which the thermal equilibration time is shortest,see an overview.[3]Actually,most of the heavy fermion materials exhibit the T-linear resistivity when they su ff er a quantum critical transition at low temperatures.Partially due to these facts,it has long been proposed that the universal time scale associated with quantum criticality could be essential to the transport in strange metals.[4]By “universal”,it means that the time scale is independent of material parameters and determined by the temperature in units of time through Planck’s constant: τP/(kBT).It was pointed out in Ref.[5]that the high transition temperature of copper-oxide superconductors can be correlated to the short time scale(referred there as Planckian dissipation)by reducing the Home’s law.More direct experimental evidence for the existence of Planckian dissipation in strange metals is the observation of similar scattering rates in T-linear region across a wide range of materials.[6]

It is natural to investigate the universal transport of strange metals by gauge/gravity duality,see some early references[7−14]and a recent review.[15]This is appealing for at least three reasons.Above all,holography can provide a controllable and quasi-particle independent method to deal with the strongly coupling systems.Next,different gravitational theories associated with different patterns of momentum dissipation provide a platform for searching universality.Last but not the least,black holes are believed to be so extreme in nature that they tend to saturate various bounds which could dominate the corresponding systems.

In a relativistic system without chemical potential,the most famous holographic result,namely the conjectured bound on the viscosity to entropy ratio,[16]can be reformulated as the bound on the diffusion constant of momentum D&/(kBT),where c is the speed of light.Loosely inspired by this,Hartnoll has proposed that the diffusion of charge and energy in incoherent metals is subject to certain similar bounds.[17]Furthermore,since the thermoelectric effect is negligible in many materials of interest,the diffusive bounds can be translated by the generalized Einstein relation into the bounds of conductivities.When the descendent bounds are saturated and the charge susceptibility is assumed to have weak temperature dependence,the T-linear resistivity and the Planckian effective timescale can be obtained.Moreover,when the temperature is high enough,the resistivity can exceed the MIR limit.

The theory of incoherent metals is full of insights,but it still su ff ers from some problems,as pointed out in Ref.[18].First,the diffusion bound is not universal as expected.[15]Second,although aiming to set up a framework beyond the MIR limit,the Fermi velocity is taken as the characteristic velocity in the theory.This is a working notation,supported by the angle-resolved photoemission measurement on the cuprate superconductors,[19]which indicates that the dispersion relation ω ∼ vF|k−kF|about the Fermi surface is still possible to be identified.However,as pointed out by Hartnoll himself,the characteristic velocity ideally should be independent with any singleparticle properties.Moreover,one may predict that an unsuitable velocity would affect the validness of the bound.For instance,in a single-band Hubbard model,[20]it was found that the use of bare Fermi velocity violates the diffusive bound by several orders of magnitude.But when replaced by its low-temperature renormalised value,the bound is satisfied at high temperatures.To address this issue,Blake proposed to take the butter fly velocity vBas the characteristic velocity in strongly coupling systems.[21]The butter fly velocity quantifies the speed of a local operator growth in time,without reference to the singleparticle picture.[22−25]Actually,a rather universal relation has been found among the butter fly velocity vB,Planckian timescale τPand the diffusivity of charge DC.[21]However,in addition to several special non-universal cases,[26−27]the particle-hole symmetry must be imposed in general1Note that the Planckian relation between butter fly velocity and thermal diffusivity seems to be more robust,[22,28−31]also see the counter examples.[32−35].At last,the strange metals that are relatively clean has been excluded in the incoherent metallic theory where the quick momentum relaxation is postulated.

In view of these problems,much effort has been made to understand and re fine the theory of incoherent metals,see the recent theoretical[36]and experimental[37]progress for examples.In this paper,we will explore the diffusive transport and its possible relation to strange metals with the help of gauge/gravity duality.We will focus on a particular combination of charge and heat currents that is decoupled from the heat current.The “heat-decoupled”(HD)current was identified in Ref.[18]recently.It can be viewed as a natural extension of a composite current that was previously proposed by Davison,Goutéraux,and Hartnoll(DGH)[38−39]for clean fluids.This is because the HD current and DGH current are equal in most of homogeneous holographic lattices.We will demonstrate that the HD current can be transported by diffusion at long distances,when the thermoelectric effect is small,large,or balanced.Thus,we have three HD diffusive modes2Note that the HD mode at thermoelectric balance has been studied in Ref.[18].But other two modes have been neglected..We will study three diffusion constants and their relation to quantum chaos in some holographic models.After that,we will assume that the existence and features of HD modes appear in a wide class of theories and describe some consequences,which may be relevant to the ubiquity of T-linear resistivity in strange metals.

2 Heat-Decoupled Current

Let us introduce three composite currents,including the incoherent current,DGH current,and HD current.Consider the response of the electric current J and the heat current JQto small gradients of chemical potential∇µand temperature∇T.The thermo-electric conductivities(σ,α,)are defined through the matrix

The DGH current is a particular combination of the electric and heat currents[3Note that the decoupled thermo-electric currents have been studied in two holographic models with momentum relaxation.[39−40]Also see a more general discussion in the Appendix of Ref.[18].8−39]

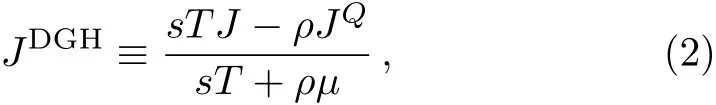
where s,ρ denote the entropy density and charge density,respectively.For a conformal field theory(CFT),it is identical with the incoherent current[38]

which is defined to decouple with the momentum,i.e.=03Note that the decoupled thermo-electric currents have been studied in two holographic models with momentum relaxation.[39−40]Also see a more general discussion in the Appendix of Ref.[18]..Here χJPand χPPare the static susceptibilities and P denotes momentum current.In this paper,we will focus on the HD current[1Note that the Planckian relation between butter fly velocity and thermal diffusivity seems to be more robust,[22,28−31]also see the counter examples.[32−35]8]

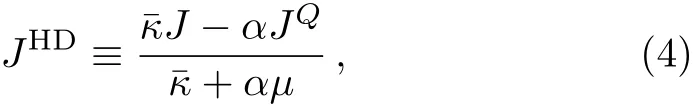
which decouples with the heat current,i.e.〈JHDJQ〉=0.The HD current is relevant to the saturation of a bound[18]

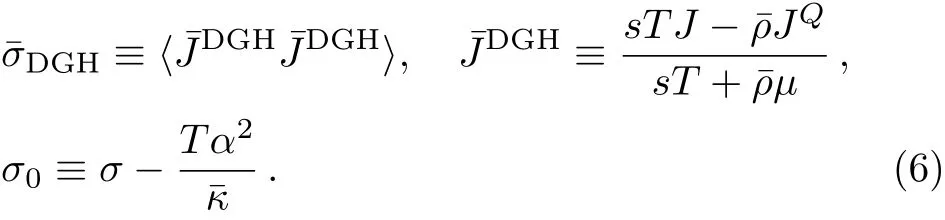
Note that the bound is almost trivial,except that it is saturated when=JHD.

3 Di ff usive Mode

Based on the conservation of the energy and the charge,the HD current respects the continuous equation

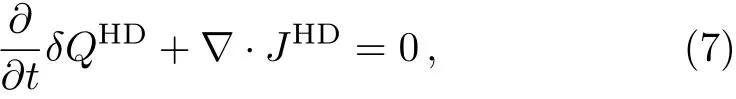
where

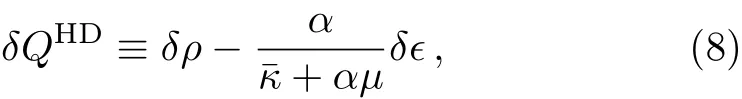
and ϵ denotes the energy density.Consider the thermodynamic identities

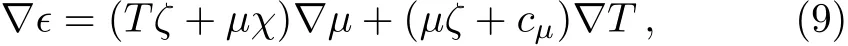
where we have defined the susceptibilities by derivatives of pressure

Combining Eqs.(1),(7),and(9),one can prove

where we have defined

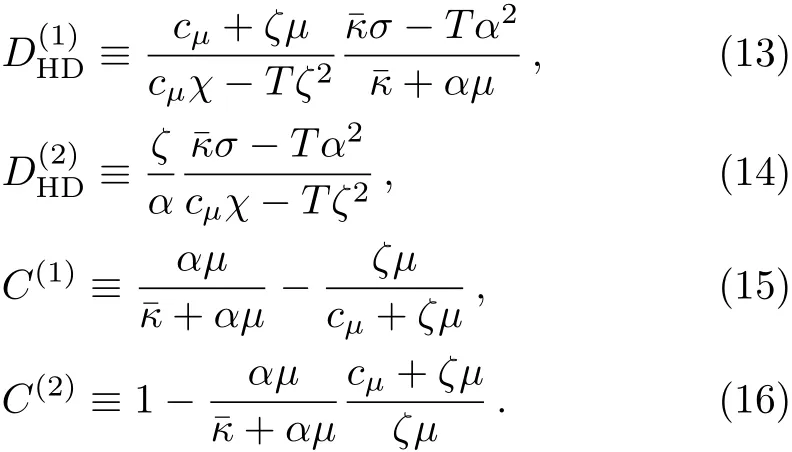
Note that Eq.(11)and Eq.(12)hold only at long distance.Following Ref.[41],the pure diffusion equation

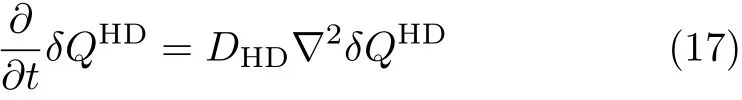
can be approximately constructed,provided that we have

Accordingly,the diffusion constant is

When both conditions in Eq.(18)are respected simultaneously,they converge to the same one

At this time,the diffusion constant can be expressed as

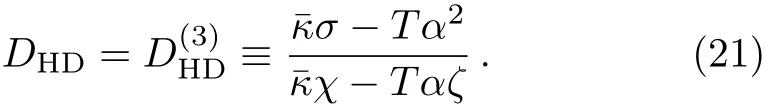
Hereto,we have revealed that there exists three HD diffusive modes in general,with different diffusion conditions and diffusivities.

Next,we will study whether the HD modes satisfy the relation

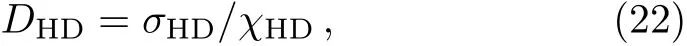
where σHDand χHDdenote the HD conductivity and susceptibility:

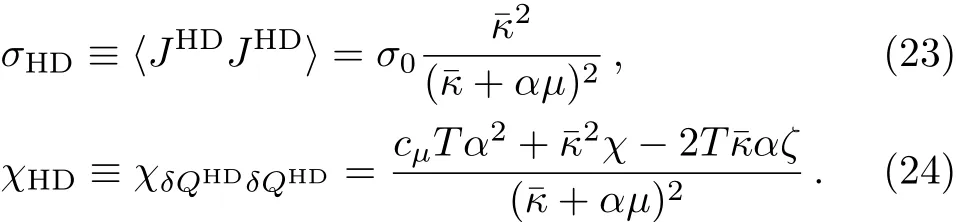
Since DC= σ/χ is well-known as the Einstein relation,we refer Eq.(22)as the Einstein-like relation.

Some remarks are in order.First,the diffusion conditions(18)require small or large thermoelectric effectand ζµ/cµ.In general,they are not correlated to the Einstein-like relation.However,we will show in next section that the Einstein-like relation may be emergent,up to an O(1)factor.Second,the diffusion condition(20)represents a special balance between the thermoelectric conductivity α and susceptibility ζ,[18]under which one can find that the Einstein-like relation= σHD/χHD holds exactly.Third,the thermoelectric balance is reminiscent of the Kelvin formula σ/χ = α/ζ.It is a good approximation to the thermopower in various contexts including strongly correlated systems.[42−44]

4 Holographic Models

In the following,we will study the HD modes based on the simplest holographic model with momentum relaxation,that is,the Einstein-Maxwell-axion(EMA)model.[45]The action is

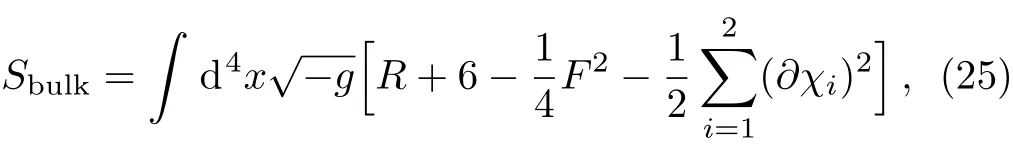
where χiare two linear axions. For convenience,we have set the AdS radius L=1 and the Newton constant 16πGN=1.This action allows an isotropic background solution

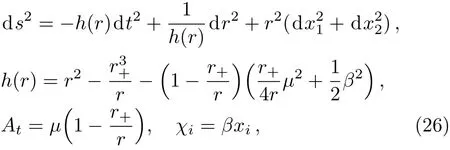
where β denotes the disorder parameter and r+the location of the horizon.We can read o ffthe Hawking temperature,entropy density and charge density:

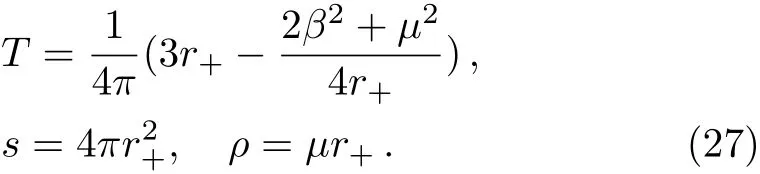
Using the Donos-Gauntlett method,the thermo-electric conductivities have been derived in Ref.[46]

We also have interest on an Einstein-Maxwell-Axion-Dilaton(EMAD)theory,which is described by the action[47−48]

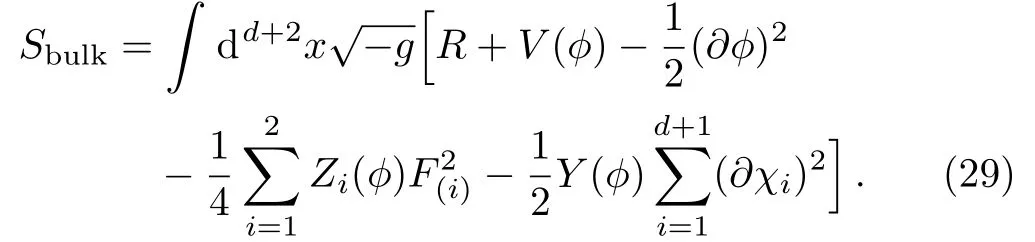
The theory consists of two Maxwell fields,(d+1)axions and a dilaton.The two Maxwell fields are supposed to have the charges(q1,q2).We impose the physical condition that the first Maxwell current vanishes.Then the physical charge density is ρ=q2.The potential and the coupling are all the functions of the dilaton:

where Λ and λi(i=0,1,2,3)denote some parameters.In Refs.[47–48],it has been found that this theory admits analytical black-brane solutions in(d+2)-dimensional spacetimes with the general dynamical critical index z and hyperscaling violating factor θ.For our aim,we only focus on a special case with(d=2,z=2,θ=0).Then the solution can be written as

where

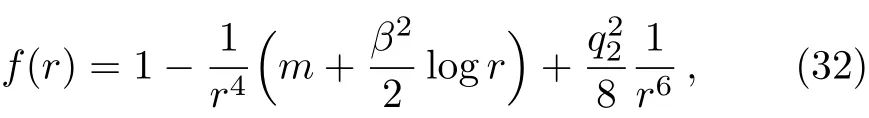
with the mass parameter m.Note that the solution indicates a logarithmic behavior due to z=2.[48]For our aim,we need to read o ffthe thermodynamic quantities

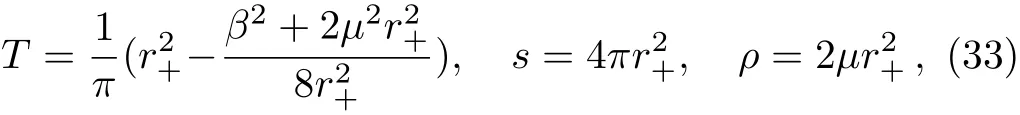
and the DC thermoelectric conductivities[47]

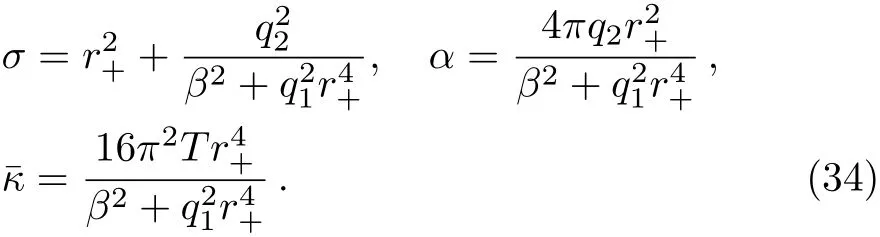
5 Di ff usivity and Chaos

Let us study when the thermoelectric effectand ζµ/cµare small or large in the EMA model.Then the diffusion conditions(18)can be satisfied.Using Eq.(27)and Eq.(28),one can calculate

The first two lines in Eq.(35)certify that there is a diffusive mode at high temperatures or strong disorder.From Eq.(13),the diffusion constant is

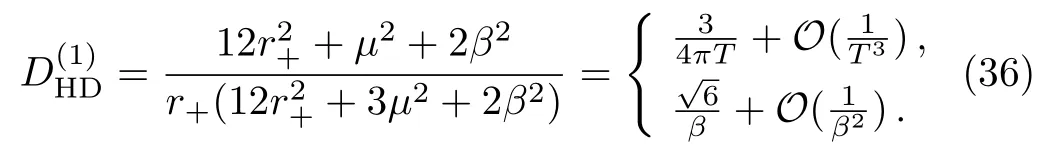
We turn to study the quantum chaos.What we are concerning is the Lyapunov time τLand the butter fly velocity vB.By constructing a shock wave near the black hole,they can be calculated by holography.[23−25,49−50]For the EMA model,they have been obtained in Refs.[21–22]: τL=1/(2πT)and= πT/r+.Then we can build up which indicates that besides the butter fly velocity,the HD diffusivity is dominated by the Lyapunov time.

According to the last line in Eq.(35),the diffusive mode also exists at low temperatures,with another diffusion constant(14).In Ref.[18],it has been shown thatand there is a general diffusion/chaos relation

Next,we check the Einstein-like relation by two ratio:

One simple but important observation of this paper is following:due to their particular structure4Note that the similar structure also appears in the Hall angle of a holographic strange metal.[51],the first ratio is close to 1 and the second ratio belongs to(1/2,3/2).As a result,the Einstein-like relation generally holds,up to an O(1)factor.

We turn the attention to the thermoelectric balance,which has been realized in Ref.[18].Here we review it briefly.Consider the Lifshitz gravity with Eq.(33)and Eq.(34).One can find that the condition(20)and Kelvin formula hold exactly.By calculating the diffusion constant(21)and the quantities in quantum chaos

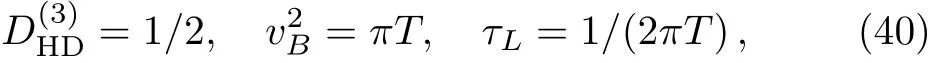
one can obtain

Before ending this section,note that≃DCat strong disorder and≃DTat low temperatures or strong disorder in the EMA model,as well as=DC=DTin the Lifshitz model.

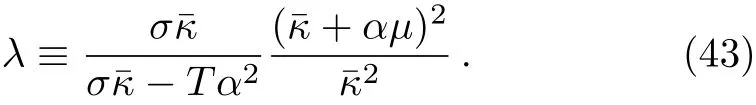
We proceed to describe some consequences of the proposed expression on the charge transport in strange metals.They can be classified by three different values of the λ-factor,corresponding to different thermoelectric effect,and in turn different HD modes and critical conditions.

6 Charge Transport

We assume that the HD mode,characterized by the Einstein-like and diffusion/chaos relations,appears in a wide class of theories under certain “critical condition”5The critical condition depends on the concrete systems.In the EMA model,it is the high temperate,strong disorder,or low temperature.In the Lifshitz gravity,it is the special critical index..As a result,we can deduce a suggestive expression from Eq.(23)that indicates the saturation of the bound(5):

Here the Einstein-like relation σHD∼ DHDχHDand the diffusion/chaos relation DHDhave been used.Also,we have introduced a dimensionless λ-factor

(i)λ ≃ 1.This requires small α and thereby the first HD mode may be relevant.In the EMA model,the high temperature is a critical condition for the HD mode,but it cannot be directly applied to strange metals,since the holographic model at high temperatures is controlled by UV CFTs.Nevertheless,due to Eq.(43),λ≃1 does not correspond to the low-temperature regime of strange metals6By observing the coefficient of the linear in T resistivity,the strange-metal phase has been delineated into the high-temperature and low-temperature regimes.[52].Moreover,as illustrated in the EMA model with strong disorder,the small thermoelectric effect often reduces the HD diffusivity to the charge diffusivity.Therefore,Eq.(42)may be reduced to DC.Obviously,these results are indicative of the theory of incoherent metals,[17]where the high-temperature regime of strange metals is focused,the fast momentum relaxation is essential,the thermoelectric effect is neglected,and the relation DCis proposed.Here the advantage is that we have not assumed any diffusion bounds which can be violated.

(ii)λ ≫ 1.Now α is large,the second HD mode can be realized,and the critical condition may be the low temperatures.

(iii)λ ∼O(1). When the diffusion condition(20)holds,the present situation is probable.This is related to the third HD mode.As illustrated in the Lifshitz gravity,the critical condition may be the special critical index.In that model,one can find 1<λ.5 in the parameter space with T&0.2µ and arbitrary β.

Collecting these results together,we can present a general predication for strange metals:when the thermoelectric effect is not very large,the scaling of σ is predominantly controlled by the HD diffusive mode(that determines DHDand χHD);otherwise more physics(that determines λ)besides the diffusion is required.More clearly,we propose to test∼ O(1)in the hightemperature regime of strange-metal phase.

One of possible “more physics” is the thermoelectric balance embodied in the Kelvin formula and the diffusion condition(20).Inputting them into Eq.(24)and Eq.(43),we can obtain λ = χ/χHD.Thus,we can retrieve DC,associated with DT.Interestingly,at this time the thermoelectric effect can be large and the momentum relaxation can be slow.This might be relevant to the recent experiment on cuprates,[37]as pointed out in Ref.[18].

7 Discussion

Without reference to quasiparticle pictures,we presented a theory of diffusive transport,which follows the spirit of Ref.[17]:the collective diffusion of charge and energy is relevant to certain bound and dominates the strange-metal transport that indicates the Planckian dissipation.The main differences include:(i)the relevant bound is trivial but universal;(ii)the butter fly velocity is taken as the characteristic velocity and it has the relation to the HD diffusivities;(iii)the diffusion may be also responsible for the ubiquity of strange metals that are relatively clean7Recently similar arguments have been presented.[59−60]and even have the considerable thermoelectric effect.

Our theory does not propose any bounds on HD diffusivities,and thereby the universality of HD modes should be limited.Nevertheless,we need to be convinced that the existence and features of HD modes are not accidental.In the Appendix,we will study two typical holographic theories,which involve the Gauss-Bonnet curvature[53−55]and anisotropy.[56−58]They are well-known counter examples of the viscosity bound but the HD modes are robust in both cases.

Acknowledgments

We are grateful to Elias Kiritsis,Xian-Hui Ge,Yi Ling,Hong Liu,Hong Lü,Sang-Jin Sin,and Yu Tian for helpful discussions.

Appendix:Typical Holographic Models

A1 Higher Curvature

The Gauss-Bonnet(GB)correction would be a dangerous source of violation for the feature that is robust in the Einstein gravity.[53−54]In the following,we will use the GB gravity as a good test for the universality of diffusive modes.

Adding the GB correction to the five-dimensional EMA theory gives

where α is the GB coupling constant.The black brane solution can be read from Ref.[55]as

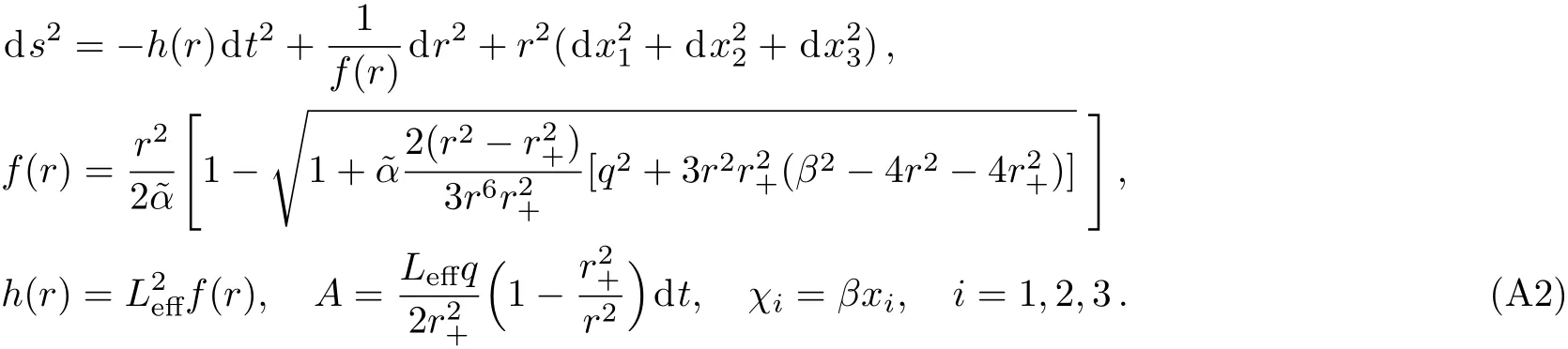
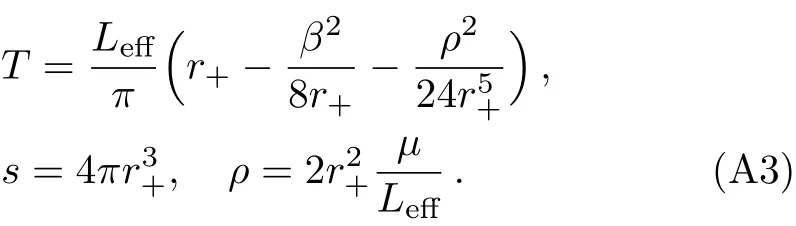
The thermo-electric conductivities have been calculated in Ref.[55]:

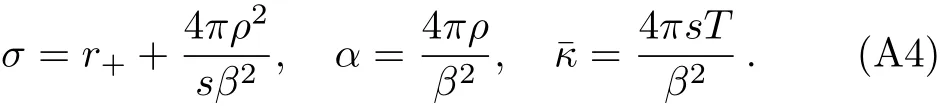
Using Eq.(A3)and Eq.(A4),the two diffusion conditions(15)and(16)can be tested by calculating two thermoelectric ratio

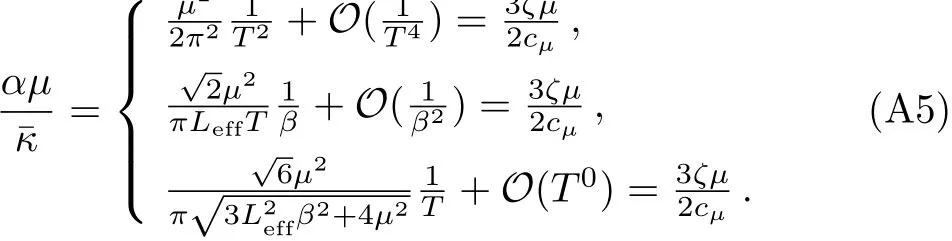
Thus,we have obtained the first diffusive mode at high temperatures or strong disorder,as well as the second diffusive mode at low temperatures.Also,one can evaluate the diffusion constants(15)and(16)

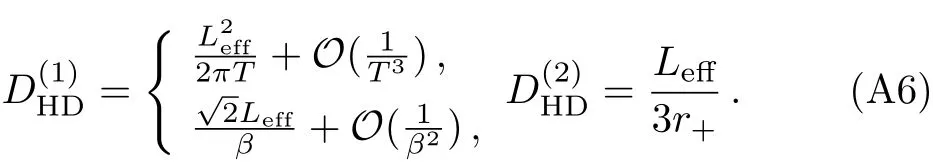
The quantum chaos in the GB gravity has been studied in Refs.[18,24].For our case,the butter fly velocity can be written as

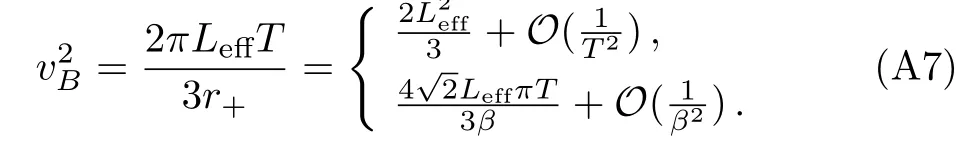
Combining Eq.(A6)and Eq.(A7),we build the diffusion/chaos relation

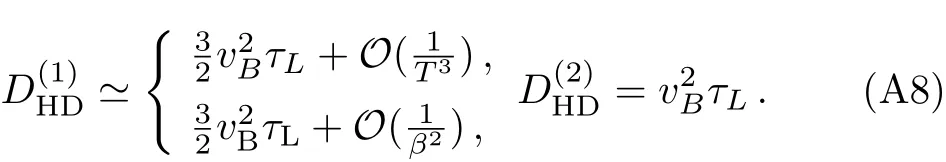
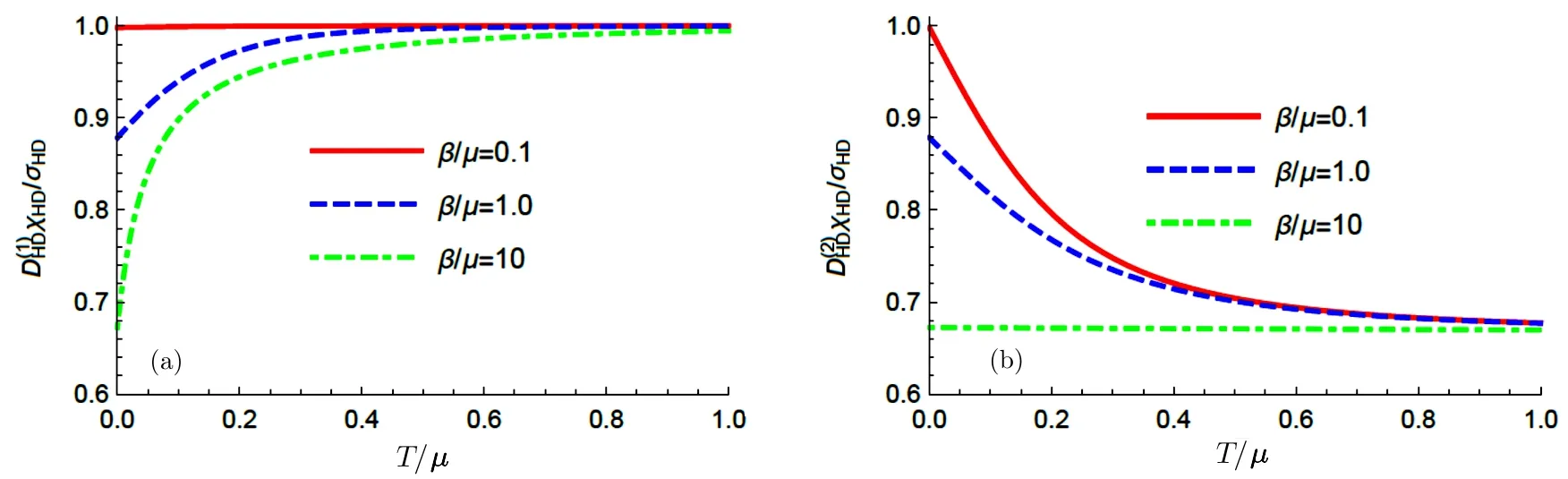
Fig.1The two ratio indicating the Einstein-like relation as functions of T/µwith α=9/100 in the GB model.The functions are bounded between 2/3 and 1.

To study the Einstein-like relation,we inspect two ratioandnumerically.Both of them are ranged from(2/3,1).Thus,the Einstein-like relation holds up to an O(1)constant.In Fig.1,we plot some typical curves.

A2 Anisotropy

We will study a five-dimensional EMAD action

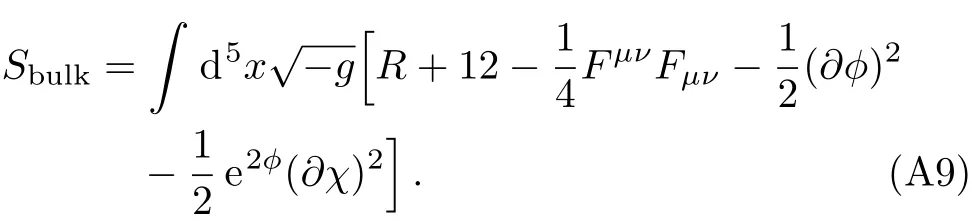
In Ref.[57],an anisotropic solution has been found numerically:

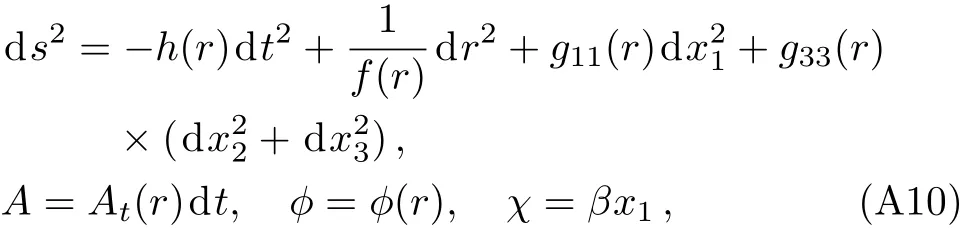
where the single parameter β simultaneously characterizes the strength of anisotropy and disorder.The analytical solution with small β also can be obtained,[57]which can be written as

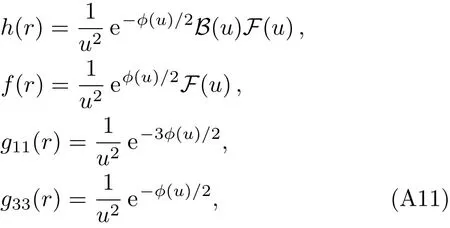
where u ≡ 1/r.The three functions(ϕ,B,F)are

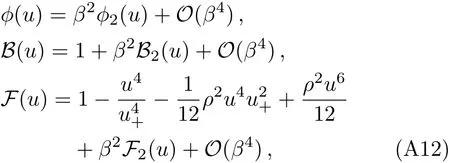
where(ϕ2,B2,F2)can be found in Eq.(135)of Ref.[57].We will use the analytical solution to study the diffusive mode.We will not use the numerical solution because the desired functions s(T,µ)and ρ(T,µ)are difficult to be solved from the thermodynamic quantities

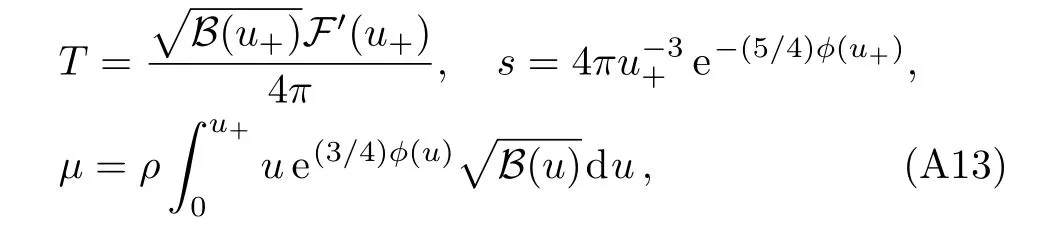
when the background has been described numerically.The thermo-electric conductivities can be read from Ref.[58],which are

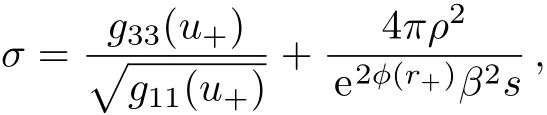
Using the analytical background solution and conductivities,we check the thermoelectric effect by Fig.2(a).Without loss of generality,we set the parameter β/µ =0.1.The regime T/µ ≪ 0.1 has been cut o ff,where β ≫ T and hence the analytical solution is not reliable.One can find that the diffusion conditions(15)and(16)hold at high temperatures and low temperatures,respectively.

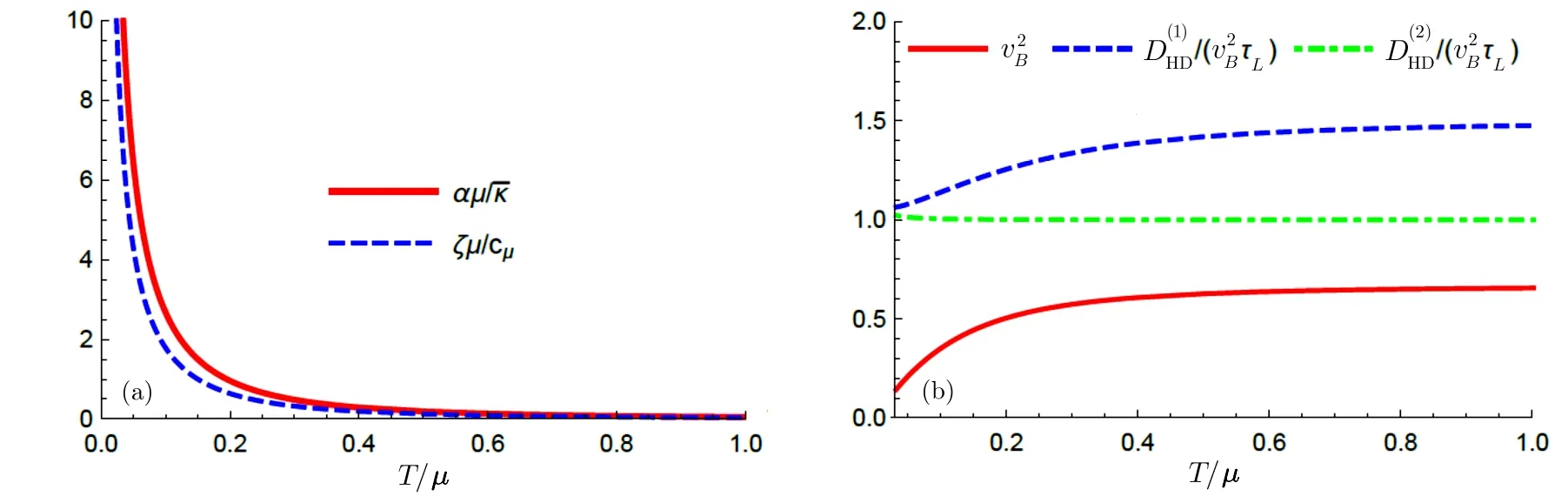
Fig.2Anisotropic model with β/µ=0.1.(a)Thermoelectric effect αµ/¯κ and ζµ/cµ.They become small and large when T/µincreases and decreases,respectively.(b)Butter fly velocity and diffusivty/chaos relation.Two of the curves saturate at high temperatures and the other always keeps constant.

Next,we will study the anisotropic chaos.In Refs.[18,50],it has been found that the form of the Lyapunov time τL=1/(2πT)and butter fly velocity=2πT/m keep the same as the isotropic model.However,the anisotropy changes the screening length by

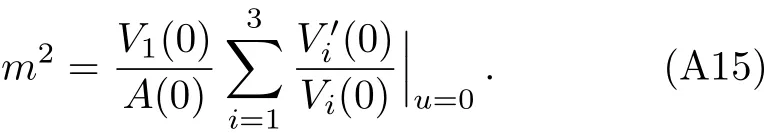
We display in Fig.2(b)the temperature dependence of the butter fly velocity and the diffusion/chaos relation.One can see

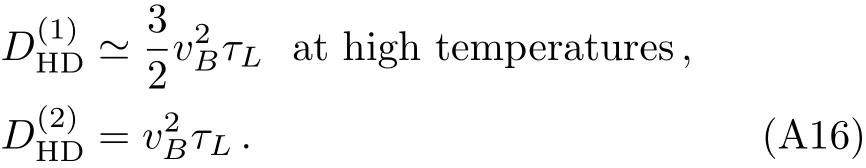
We turn to study the Einstein-like relation. By scanning the parameter space,we find that two ratioandare still bounded between(2/3,1).Their evolution as the function of T/µwith β/µ =0.1 is similar to the one shown in Fig.1.