变压器绕组变形的纳秒脉冲频率响应仿真研究

张延寿

(中原利达铁路轨道技术发展有限公司，河南 荥阳 450000)

0 引 言

变压器是电力系统中最为核心的输变电设备，其安全稳定运行直接影响电力系统的安全性和可靠性[1]。然而随着电网容量和规模的不断扩大，由于绕组变形造成的变压器短路故障呈上升趋势[2-4]。国家电网公司统计数据表明，110 kV及以上等级的变压器因短路故障而损坏的比例高达36.4%[5]。故障特征多为在短路电流所产生的轴向力和径向力的作用下，变压器绕组发生扭曲、倾斜、塌陷、鼓包和位移等不同程度的变形[6]，且具有一定的累积效应。随着故障严重程度的增加，变压器或因此突发灾难性事故，导致巨大的经济损失。

为此，国内外学者针对变压器绕组变形故障检测开展了大量的研究工作。目前离线电气检测方法广泛运用，根据测试原理的差异，可分为两大类：一类是通过测量并分析绕组的电阻、电容和电感等参数的改变量，来判断绕组的变形情况，例如短路阻抗法、电容量变化法和直流电阻变化法等[7]；另一类则是通过分析绕组的响应特性来实现检测，例如低压脉冲法、频率响应分析法和传输函数法等[8-9]。这些离线检测技术已取得了相当多的研究成果，但在线检测技术仍处于研究阶段，如何实现快速、可靠、便捷的在线检测技术尚待解决。

频率响应分析法(Frequency Response Analysis，FRA)能够快速、有效、无损检测电力变压器绕组变形。由于这些优势，各国学者也致力于将其应用于在线故障的检测。传统的正弦频率响应法在离线检测应用较多，难以满足电气设备在线检测与状态评估的发展趋势。由于在线脉冲频率响应法持续时间短、能量小，几乎不对变压器的正常运行造成影响，该方法具有实现在线检测的巨大潜力[10]。因而本文提出一种变压器绕组变形的纳秒脉冲频率响应检测方法，通过电路仿真得到绕组在纳秒脉冲激励下的时域响应，再使用快速傅里叶变换算法(Fast Fourier Transform，FFT)处理时域信号，获得其频率响应图谱，由此实现绕组状态评估。

1 纳秒脉冲频率响应基本原理

纳秒脉冲激励信号含有丰富的频率分量，其响应信号能反映绕组网络模型的特性，即可得到宽频范围的转移函数(Transfer Function，TF)，即频率响应曲线，从而实现绕组变形故障的诊断[11-12]。在高频激励下(>1 kHz)，变压器铁芯的励磁作用将消失，此时其绕组可等效为一个由分布的电感、电容和电阻构成的线性二端口网络模型。当在绕组的一端施加纳秒脉冲激励电压信号Vin，在绕组另一端可得到其响应信号Rout。当绕组受到短路电流造成的巨大电动力(主要分为辐向力、轴向力和联合力等)，发生弯曲、倾斜、鼓包、螺旋形变和重叠扭曲等变形[13]。由受绕组和媒质的几何尺寸和特性决定的网络模型的分布电感、电容和电阻参数依据将会发生变化。这将会直接导致绕组的网络模型的脉冲频率响应曲线TF发生改变，因此可将被测绕组的脉冲频率响应曲线与参考频率响应曲线进行对比而开展绕组变形诊断。

Vin(f)=f[Vin(t)]

(1)

Rout(f)=f[Rout(t)]

(2)

(3)

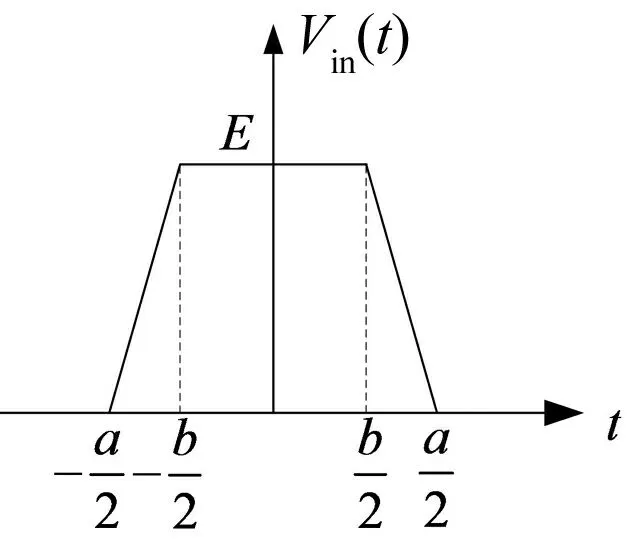
图1 简化的纳秒脉冲时域波形

式中:Vin(t)和Vin(f)分别为纳秒脉冲激励信号的时域及其频域表示形式；Rout(t)和Rout(f)分别为绕组的脉冲响应电压/电流信号的时域及其频域表示形式；f函数为将时域信号变换为频域信号的算法，目前通常采用快速傅里叶变换算法FFT；TF为以增益形式表示的绕组频率响应幅值曲线。

实际工程中纳秒脉冲的频谱分布受波形前后沿及脉宽的影响。考虑到方波脉冲的前沿和后沿差别不大，为简化计算，在此假设纳秒脉冲前后沿相等且线性，如图1所示，其时域表达式为：

(4)

图2 纳秒脉冲的频谱分布

式中：E为激励脉冲的幅值;b为脉冲宽度，上升沿和下降沿相等，均为a/2。通过傅里叶变换，可得到脉冲电压的频谱，表达式如下(频谱分布如图2所示)。

(5)

式中：j为虚数单位;ω是谐波的角频率。

在图2中，方波脉冲频谱的第一个零点2π/[T+(a-b)/2]以内频段，需要至少覆盖用于绕组变形频率响应检测的频段范围0～1 MHz，否则激励信号的高频能量难以引起绕组等值电路的谐振。由于频率响应曲线在过零点处，将出现伪谐振点，严重影响绕组变形的判断，所以选择脉冲频谱的第一个零点应当越大越好，以此避免伪谐振点的出现。当脉宽固定时，脉冲前沿越陡，其频谱第一个零点值越大；当脉冲前沿固定时，脉宽越窄，其频谱第一个零点值越大[14]。但脉冲越陡，脉宽越窄，对于脉冲发生器的研发就越严苛。综合考虑，为尽量使第一个伪谐振点出现在更高频率，以及降低对脉冲发生器的要求，本文选取上升沿50 ns、脉宽200 ns的脉冲作为激励信号。

2 基于Pspice的纳秒脉冲响应仿真

本文以一台单相变压器作为研究对象，对其纳秒脉冲的频率响应进行仿真分析[15-16]。该变压器等效电路如图3所示:高低压侧均由10饼绕组构成，其中每一饼单元的等效电路包含串联电阻Rs和串联电感Ls，以及相邻两饼间的电容Cs和饼间电导Gs；高低压绕组间的绝缘状态由绕组间等效的电容CHL和介质电导G表征；饼间互感用Mij表示。此外，低压绕组和铁芯之间、高压绕组和外壳之间的绝缘介质(变压器油)由等效的对地电容Cg和介质电导G模拟，绕组等值电路参数如表1[17]所示。在Pspice软件中建立该变压器的仿真电路。图4所示为高、低压侧第一饼电路图。

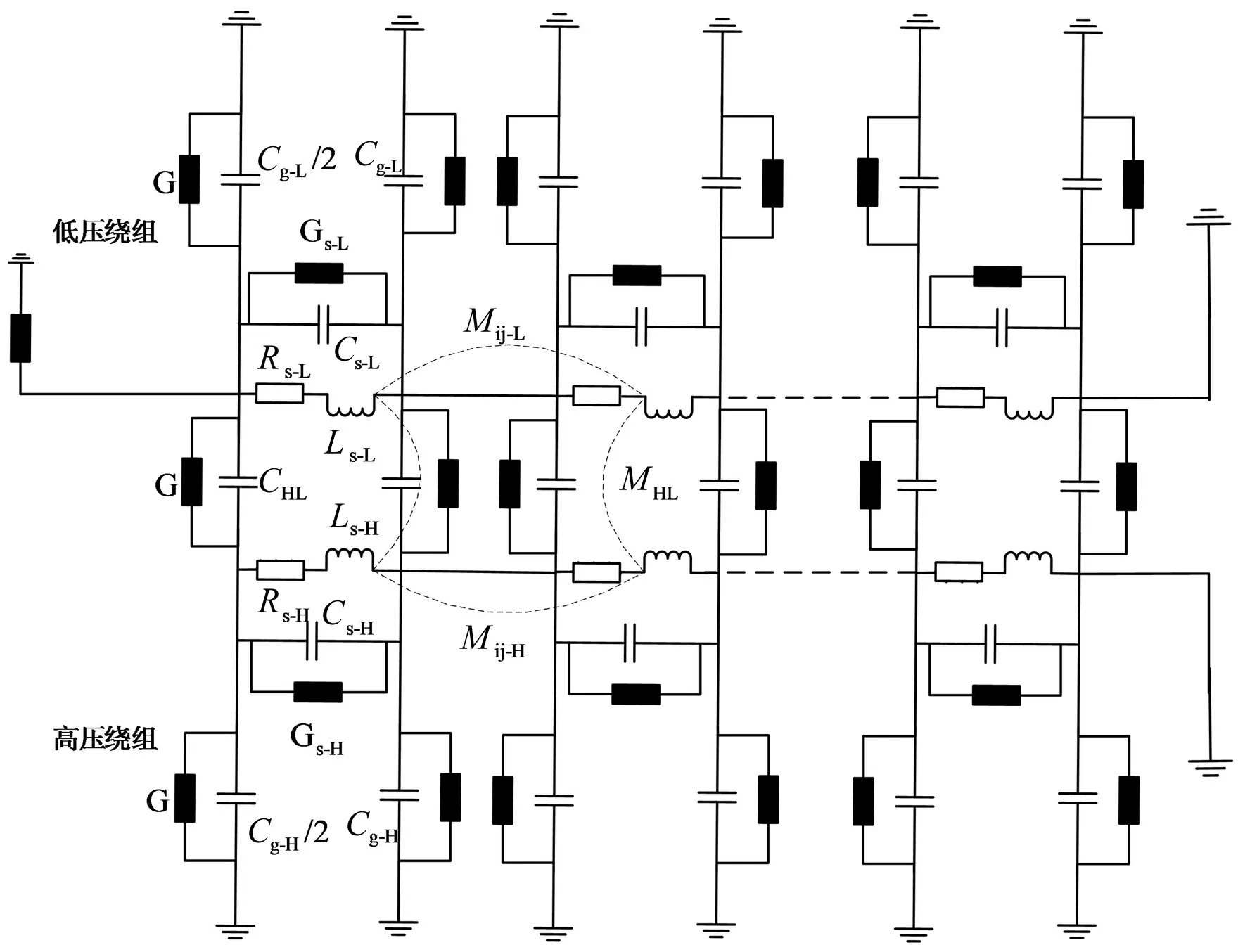
图3 变压器绕组等效电路模型

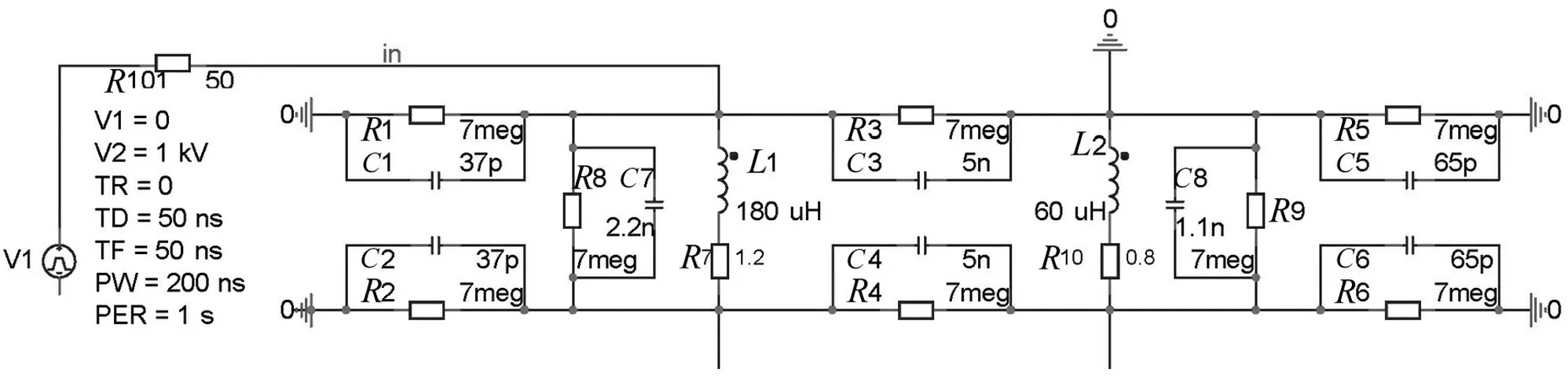
图4 变压器绕组仿真电路局部图

参数Rs/ΩLs/μHCs/ nFCg/ pFCHL/ nFG-1/ MΩ高压绕组1.21802.203757低压绕组0.8601.116557

2.1 健康绕组频率响应曲线获取

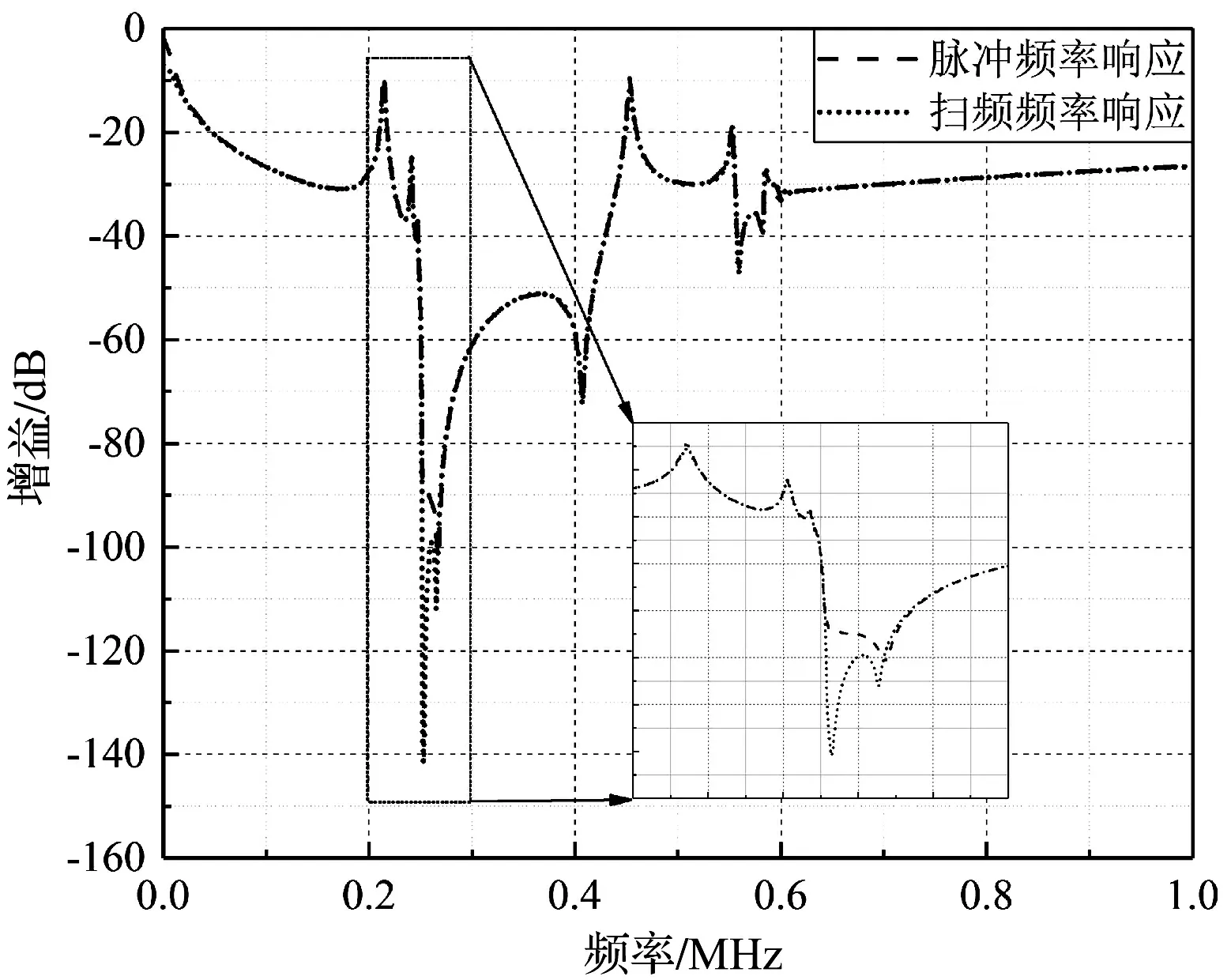
图5 扫频与脉冲频率响应曲线对比

在仿真电路中，将低压侧绕组两端分别接地，以此表示低压绕组短路接地。在高压侧施加纳秒脉冲，并测量高压侧绕组两端的电压信号。仿真采样时间设置为1 ms，采样间隔为10 ns。对采集到的时域响应电压信号进行FFT变换，再利用式(3)获得高压绕组在纳秒脉冲激励下频率响应曲线TF。另外为获得高压绕组的扫频响应曲线，则在高压侧施加正弦电压，利用扫频模块可进行仿真。设置正弦电压扫描频率范围为[1 Hz, 1 MHz]。两种方法获得的绕组频率响应曲线对比如图5所示。

2.2 故障状态绕组频率响应曲线获取

图6 幅向变形故障绕组脉冲频率响应曲线

若高压绕组其中一饼发生幅向变形，则该饼绕组所包围的面积将发生变化，且对地和对低压绕组以及对相邻绕组的距离将发生变化。如发生了向外凸起的鼓包，则该饼绕组所匝链的磁链将增加，即该饼绕组的自感Ls以及对其他绕组的互感Mij将增加。由于绕组相对地的距离减小，则对地电容Cg减小，对低压绕组的电容CHL相应增加。因此，在电路模型中改变第5饼绕组的自感Ls以及相对于其他绕组的互感M5j，同时改变对应的电容值，利用脉冲频率响应法获取包含故障绕组的高压绕组频率响应曲线如图6所示，其中幅向变形1和幅向变形2分别表示向外鼓包和向内塌陷的故障。

图7 轴向变形故障绕组脉冲频率响应曲线

当绕组发生轴向弯曲变形时，对应的绕组包围的面积不会发生变化，但将导致相对于邻近绕组的距离变化。因此，饼间电容Cs会发生变化。为在仿真种模拟该种故障类型，改变电路模型中第5饼绕组相对于邻近绕组的电容Cs。施加纳秒脉冲后，获得轴向变形故障状态下高压绕组脉冲频率响应曲线如图7所示，其中轴向变形1和2分别表示绕组发生轴向上弯曲和轴向下弯曲故障。

为模拟绕组发生短路故障时的状况，在仿真电路模型中，将短路绕组两端短接即可。故将电路模型中将第5饼绕组的两端短路，并施加纳秒脉冲，获得短路故障状态下高压绕组脉冲频率响应曲线如图8所示。

3 仿真结果分析

通过频率响应曲线诊断绕组变形的实质是通过其谐振峰、谷的位置以及幅值和相位信息来实现诊断，其余频段为冗余信息[18]。故本文从脉冲频率响应曲线谐振点出现的频率以及谐振点个数的变化进行分析。

由图5可以看出，利用纳秒脉冲注入获取的健康绕组的频率响应曲线与扫频频率响应曲线在[1 Hz，1 MHz]频率段基本重合，在250 kHz附近，脉冲频率响应曲线的增益比扫频频率响应偏大，但是谐振点的位置一致，这不会影响对于绕组状态的判断。因此，脉冲频率响应法在理论上可以替代传统扫频频率响应法作为绕组频响曲线的获取方法。

图8 短路故障绕组脉冲频率响应曲线

根据图6～图8所示的不同故障状态下高压绕组脉冲频率响应曲线，当单饼绕组发生轴向变形故障和幅向变形故障时，此变压器的等效电路模型频率响应曲线整体趋势不会发生大幅度的变化。这主要是由于相对于整个电路模型来说，单饼绕组的故障较小，对整个频率响应曲线的影响也较小。但是在局部[200 kHz，300 kHz]会发生谐振点偏移，或者新的谐振峰出现。

当绕组若发生饼间短路时，脉冲频率响应曲线在全频段[1 kHz, 1 MHz]出现了偏移，这可能是由于饼间短路对于10饼绕组的电路模型来说故障程度是很严重的。另外，在低频段和在高频段的谐振点位置偏移方向是相反的。

当绕组出现外凸以及内陷幅向变形的时候，绕组的自感大小变化是相反的，但是反应在脉冲频率响应曲线上，谐振点的偏移并没有明显的规律，这可能是由于等效电感的变化的同时，相应的等效电容也发生了变化，并不能在频率响应曲线上直接反映出电感的变化。

当绕组出现轴向下和轴向上弯曲变形故障时，绕组频率响应曲线中谐振点的偏移方向不是相反的，因此由频率响应曲线不能由谐振点的偏移情况直接判断不同的轴向故障类型。

4 结束语

本文对纳秒脉冲频率响应法用于检测绕组故障进行了仿真分析。首先基于理论分析了纳秒脉冲的参数选择依据，选择上升沿和下降沿均为50 ns、脉宽200 ns的脉冲作为仿真的激励源;然后建立了110 kV单相变压器10饼绕组的等效电路模型，通过扫描频率和脉冲频率响应两种方法获得了绕组的频率响应曲线，证明了由脉冲频率响应法获取绕组频率响应曲线的可行性;最后分析了幅向变形故障、轴向变形故障以及短路故障对于脉冲频率响应曲线的影响，发现对于此电路模型，短路故障会引起曲线的整体偏移，且在高频和低频段谐振点位置的偏移方向是不一样的,而幅向变形故障和轴向变形故障不会引起曲线的整体变化，但在局部[200 kHz，300 kHz]会出现谐振点的偏移及出现新的谐振点,频率响应曲线无法直接判断不同幅向变形或轴向变形的类型。这些结论可以为绕组变形的模式识别提供一定的参考。