多孔进水结构对蓄热水箱热特性的影响
(1 上海理工大学能源与动力工程学院 上海 200093; 2 住房和城乡建设部科技与产业化发展中心 北京 100835)
随着全球环境日益恶化,可再生能源受到高度关注。太阳能技术的使用日趋成熟,且应用领域广阔[1-3]。在太阳能热电联产系统和太阳能热水系统中,蓄热技术均应用广泛,是提高太阳能利用效率的关键技术之一。蓄热水箱是太阳能系统中的核心设备,蓄热水箱性能的高低,不仅对系统蓄热量有关键作用,而且对系统效率有决定性的影响,因此,有必要深入研究蓄热水箱的性能[4-6]。
国内外学者研究发现,由于水的密度随水温的升高而降低,由此形成的浮生力会驱动温度较高的水流向水箱顶部,同时温度较低的水会流向水箱底部,并在冷热水间形成温跃层,形成水箱的温度分层,从而提高系统效率[7-9]。
诸多学者使用数值模拟和实验的方法对分层蓄热水箱进行了深入研究。A. Castell等[10]在使用了一种喇叭形进口均流器的条件下,对比分析了理查德森数(Ri)、混合数(MIX)、佩克莱数(Pe)及雷诺数(Re)等表征分层水箱性能的参数,发现用Ri表征分层水箱性能最为合理。N. Altuntop等[11]基于标准k-ε湍流方程,采用FLUENT对具有不同结构折流板的水箱进行了数值模拟,结果表明,折流板对水箱的热分层特性提高效果显著,且具有环状结构折流板的水箱性能最佳。A. A. Hegazy[12]研究了楔形、多孔形及条缝形进口结构对水箱分层特性的影响,结果表明,相同进口体积流量及水箱长径比时,具有条缝形进口结构的水箱效率最高。
韩延民等[13]阐述了热分层的形成原因、破坏因素以及对热分层效果的评判指标,结果表明,水箱性能的提高,是由于导流板改善了水箱内水的流道,并进一步降低了蓄热水箱的湍流耗散程度。李舒宏等[14]基于80 cm×40 cm×40 cm方形水箱,研究了不同进水结构对水箱用能效率和内部温度分层特性的影响,当进口体积流量分别为5 L/min和10 L/min时,开孔型进口比直接进口的水箱用能效率分别提高21%和36%,表明该进水结构可明显提高水箱内部的热分层特性。孙东亮等[15]分别基于温度分层模型和均温模型,对太阳能水箱蓄热供暖系统进行了模拟研究,得到温度分层模型可以准确预测系统性能。郝新月等[16]研究了双分层水箱太阳能喷射制冷系统特性,结果表明,该制冷循环较传统水箱太阳能喷射制冷循环日产冷量提高36.8%。
综上所述,蓄热水箱中的分层可以提高热水出水量,进而提高整个太阳能集热系统效率;同时水箱分层越好,所具有的火用值越高,水箱分层良好与完全混合相比,火用值更高。而降低进口水流对高温水箱内热水的扰动是提高水箱热分层特性的关键因素之一。本文设计了一种具有抑制进口水流对高温水箱内热水扰动的均流器,并搭建了蓄热水箱热分层特性实验台,同时基于混合数法、理查德森数法和填充效率对蓄热水箱的热分层特性进行定量分析,研究结果可为太阳能水箱进出口结构设计提供参考。
1 实验系统
实验主要研究新型进口结构对于水箱分层及其效率的影响。3种蓄热水箱结构如图1所示,分别为直接进口结构水箱、三层孔板结构水箱及均流器结构水箱。水箱箱体为不锈钢材料,顶盖通过螺栓与箱体联接,以便对水箱结构进行更改。本文设计的分水器结构如图2所示。

图1 3种蓄热水箱结构Fig.1 The structures of three types of hot water storage tanks

图2 分水器结构Fig.2 The structure of stratifier
图3所示为实验系统原理,该实验系统主要由涡轮流量计、变频泵、阀、高温蓄热水箱及恒温水箱组成。蓄热水箱的容积是影响水箱分层的重要参数之一,尤其蓄热水箱的高径比,众多学者研究了高径比对水箱分层特性影响。由文献[10,17]可知,水箱高度越高,其内部分层效果越好,但同时也会增强水箱与周围环境的对流换热,增大水箱的热损失。根据文献[10,17],水箱的高径比为1~4时,效果最佳,考虑水箱的实际使用环境,本文选择水箱的高度为60 cm、直径为35 cm、长径比为1.7的不锈钢圆筒,并在其内部放置一根功率为1.5 kW的电加热器,该水箱的有效容积为60 L。水箱共布置16根铂电阻,型号为OMEGA PR-10-2-100-1/8-6-E, 精度为±(0.15+ 0.002|t|) ℃。其中桶壁沿高度方向均匀布置14根铂电阻,每根铂电阻深入桶内10 cm,铂电阻间距为4 cm,如图3所示,用于测试水箱各层温度分布。水箱顶部为高温热水出口、底部为低温冷水进口,分别位于水箱顶部和底部的中央位置,此外,在进、出水口处再分别布置一根铂电阻,用于检测水箱的进出口水温。本文采用Agilent 34970为测量数据记录仪,设定采集时间间隔为5 s。实验系统中体积流量测量采用OMEGA FLR1013-D,测量精度为±1%。为了减少漏热对实验结果的影响,本实验系统采用导热系数为0.024 W/(m·K)的保温材料,主要对高温蓄热水箱及进、出水管路进行保温。恒温水箱的温度范围为-120~100 ℃,精度为±0.1 ℃,以确保进口水温恒定。热水回收水箱用于回收来自蓄热水箱的高温出水,容积为200 L。在热水回收水箱的左侧上下分别有一个补水和回水口,以保证系统的水量充足。
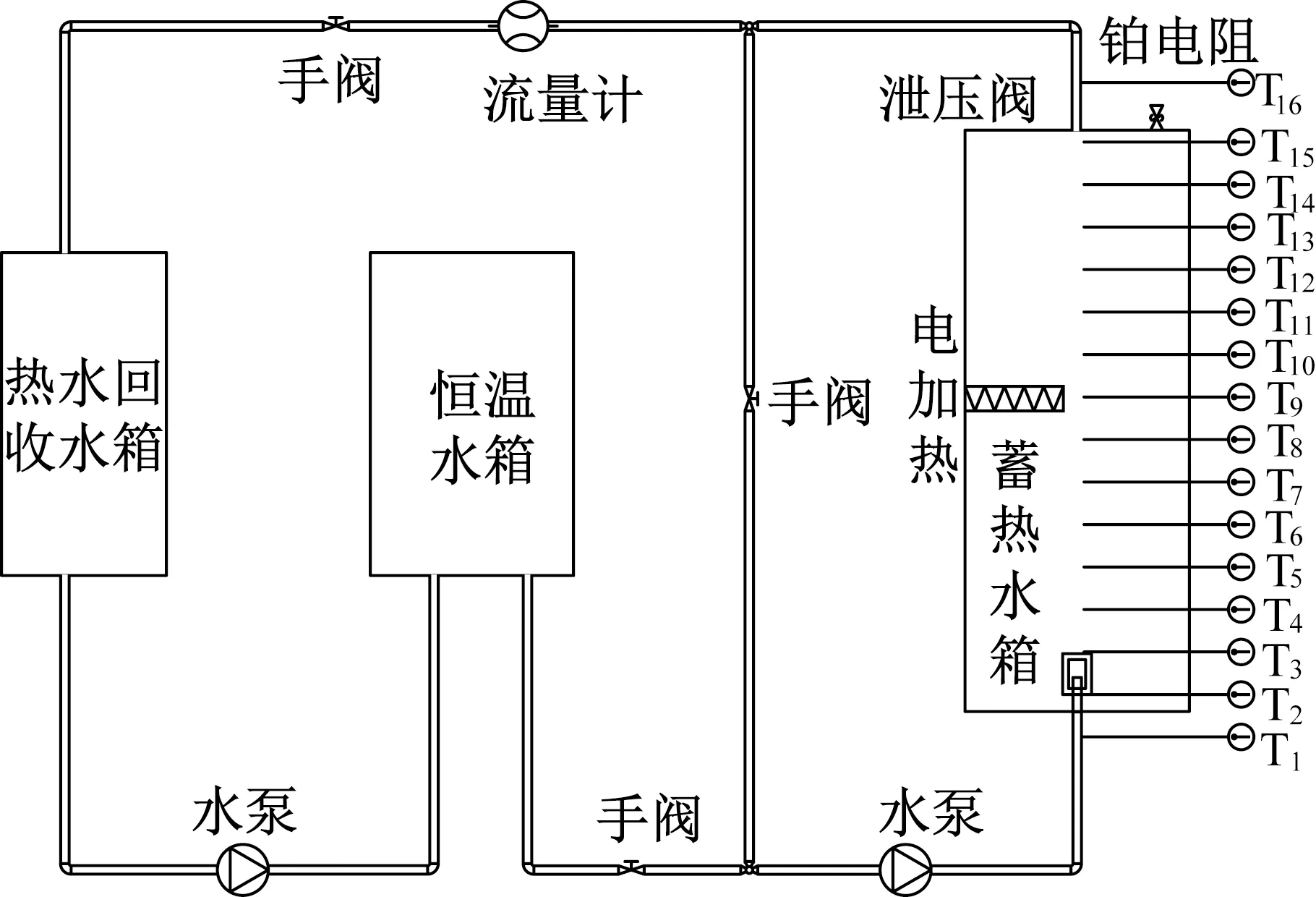
图3 太阳能分层水箱热力学特性实验系统Fig.3 Experimental system of thermodynamic characteristics of a solar water storage tank
使用电加热棒将水箱内水温加热至约70 ℃,由于冷热水密度不同,导致水箱内上层水温较高,下层水温较低,需要使用变频水泵进行循环使水温分布均匀,实验时,当水箱顶部与底部温差小于0.5 ℃时,即认为水箱内水温达到均匀。此外,设定恒温水箱温度为10 ℃,即为水箱的进水温度。从开始进水瞬间记录各温度点的温度,直至出水温度与进水温度近似相等时,停止数据采集。
本文实验工况为初始温度70 ℃,进水温度10 ℃,流量分别为1、2、3、4、5、6 L/min时的热分层特性,共计18组实验,每组实验重复3次,以确定实验数据的准确性。
2 计算模型
国内外学者提出多种方法来表征水箱内的分层效率,两种最基本的方法是密度法与温度法。A. Castell等[10]用最常用的无量纲数,如MIX、Ri、Ratio H/D、Pe和Re来表征水箱内的热分层。Pe和Re无法描述水箱内的热分层;Ratio H/D是影响热分层的重要因素,但无法表征热分层的实际程度,且并未考虑流体温度的不同;Ri用于计算对比热分层,如不同入口体积流量下的水箱内热分层的区别;MIX用于计算水箱内给定时间点的热分层,其值变化范围为0~1,表征不同程度的热分层,它对温度的微小变化极度灵敏[10]。
2.1 混合数法
E. Andersen等[18]提出了混合数的概念,如式(1)所示。混合数忽略了储热水箱的热损系数,并建立在箱内能量与温度分布水平的基础上。Mexp为计算值,且与Mstratified和Mfull-mix相关。MIX用于计算水箱内给定时间点的热分层,取值范围为0~1,表征不同程度的热分层。当水箱内冷热水为理想分层时,MIX=0;而当水箱内冷热水为充分混合时MIX=1。
(1)
其中,
(2)
Ei=ρVicpTi
(3)
假设Mstratified具有和实验水箱相同的总能量,并定义Thot与Tcold为实验值,即Thot=70 ℃,Tcold=10 ℃。
Estratified=Eexp
(4)
其中,
(5)
Estratified=VhotρcpThot+VcoldρcpTcold
(6)
VT=Vhot+Vcold
(7)
斜温层的位置ystratified由式(8)确定:
(8)
根据Vhot与Vcold,完美分层水箱的动量为:
(9)
完美混合时水箱的能量与实验水箱的能量相等:
Efully-mixed=Eexp
(10)
完美混合时水箱的动量:
(11)
其中,
Efully-mixed=ViρcpTfully-mixed
(12)
2.2 理查德森数
Ri表征浮力与混合力的比率,广泛应用于描述分层特性[19-20];Ri越小表示水箱内冷热水充分混合,而Ri越大则表示水箱内冷热水完美分层。
(13)
其中,
(14)
2.3 填充效率
Ri和MIX均可以用来表征水箱的热分层特性,但也存在各自的缺点。MIX未考虑体积流量对水箱分层特性的影响,而Ri只能从质而不能从量上分析水箱的分层特性,故需要完善表征水箱热分层特性的参数。本文根据水箱出口水温,并基于热力学第一定律,综合体积流量、初始水温及进口水温,提出填充效率的方法来表征水箱的分层特性。具体解释如下:
(15)
完美分层水箱的能量:
(16)
填充效率:
(17)
填充效率(ξ)取值范围为0~1,表征不同程度的热分层。ξ=0代表充分混合水箱,即冷热水层间的温度梯度为0,无热分层;ξ=1代表完美分层水箱,即冷热水层间的温度梯度无穷大,完美分层。ξ越大,代表水箱的可用能越多,水箱的热效率越大。
2.4 无量纲时间
为了便于分析,定义水箱的无量纲时间t*为:
t*=τ/σ
(18)

(19)
3 实验结果与分析
3.1 理查德森数分析
温度不同,传热介质的密度也不同,因此,在重力作用下形成具有驱动作用的浮升力,使水箱自下至上形成温度分层。对于上述情况,大多采用Ri(Ri=Gr/Re2)评价其影响程度[13]。
Ri是表征浮升力与惯性力之比的量度,当Ri≤0.1时为纯强迫对流。研究表明,当Ri≤3.6时,水箱进水口的结构对水箱内温度分层产生一定影响;而当Ri>10时,由于进水混合对水箱分层的影响很小,可忽略进水口结构对水箱内温度分层的影响。
由Ri的计算式可知,对于结构固定的水箱,当流体温度一定时,其Gr不变,而由于进水口结构的不同,其Re(表征惯性力)是改变的。因此,当Ri较小时,水箱中高、低温水之间的混合程度会随Re的提高而增强,进而降低水箱温度分层的效果。
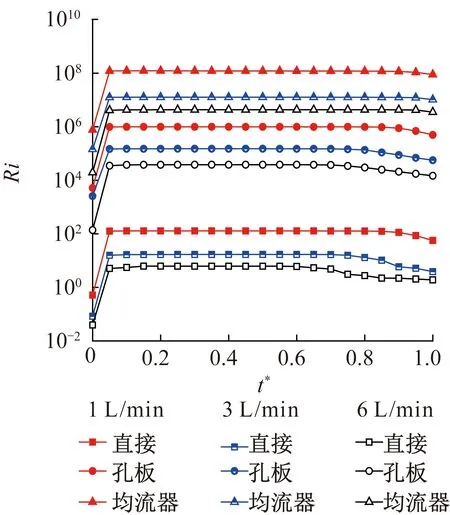
图4 不同体积流量下不同进水结构对Ri的影响Fig.4 The effect of different inlet structures on Ri under different volume flow rates
图4所示为不同体积流量下不同进水结构对Ri的影响。在图4中,分别对比了直接进口结构水箱、三层孔板结构水箱及均流器结构水箱在1、3、6 L/min时Ri的变化。不同进水结构的水箱Ri的衰减时刻随着进口体积流量的增大而提前,当进口体积流量为1 L/min时,直接进口结构水箱、三层孔板结构水箱及均流器结构水箱的衰减时间点分别为0.85、0.85和0.9;当进口体积流量增加为3 L/min时,直接进口结构水箱、三层孔板结构水箱及均流器结构水箱的衰减时间点分别为0.75、0.8和0.85;当进口体积流量增加为6 L/min时,直接进口结构水箱、三层孔板结构水箱及均流器结构水箱的衰减时间点分别为0.6、0.7和0.8。此外,当进水流量为6 L/min时,均流器结构水箱的Ri=4×106,而直接进口结构水箱和三层孔板结构水箱的Ri分别为6和4×104。说明均流器结构能明显提高水箱的热分层性能,原因是进口水经过分水器后,流速下降且水流方向变成流向水箱底部,使其与水箱底部的热水充分进行热交换,降低底部水温,水箱形成热分层,进而提高了水箱的热分层程度。
3.2 混合数分析
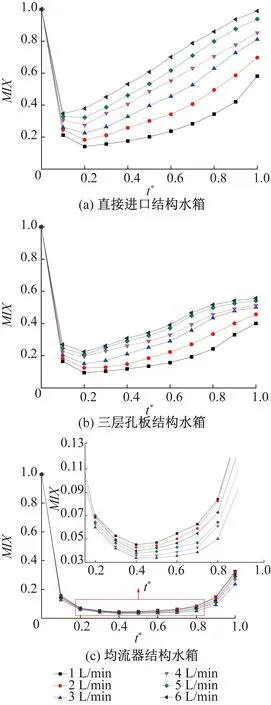
图5 不同体积流量下MIX随无量纲时间的变化Fig.5 The variation of MIX with t*under different volume flow rates
图5所示为不同体积流量下不同进水结构水箱对MIX的影响。在图5中,分别对比了直接进口结构水箱、三层孔板结构水箱及均流器结构水箱在1、2、3、4、5、6 L/min时MIX的变化。由图5(a)、(b)可知,直接进口结构和三层孔板结构水箱的MIX随着进水流量的增大而减小,并在t*=0.2时达到最小值,此后随着放水过程的进行逐渐增大。说明直接进口结构和三层孔板结构水箱的热分层程度随进口体积流量的增大而减小,这主要是由于进口体积流量的增加,破坏了冷热水的分阶层,并强化了水箱中冷热水的混合程度,使水箱的斜温度层厚度增加,进而使水箱的分层效率降低,且直接进口结构水箱MIX的增幅要大于三层孔板结构水箱,说明孔板结构对冷热水的混合起到了一定的削弱作用,提高了水箱的热分层程度。由图5(c)可知,均流器结构水箱的MIX随着进口体积流量的增大先减小后增大,并在t*=0.5时达到最小值,此后随着放水过程的进行逐渐增大。进口体积流量分别为1 L/min和2 L/min时的MIX均大于其他体积流量,这是因为流速较低时,出水时间长,水箱水层间导热和沿桶壁导热的作用。当进口体积流量为3 L/min时,水箱的MIX最小。由图5还可知,在水箱的放水过程中,均流器结构水箱的稳定状态时间(图5(c)中t*=0.2~0.8)要明显长于其他两种进水结构的水箱,表明该种进水结构的水箱具有较好的热分层特性。
3.3 填充效率分析
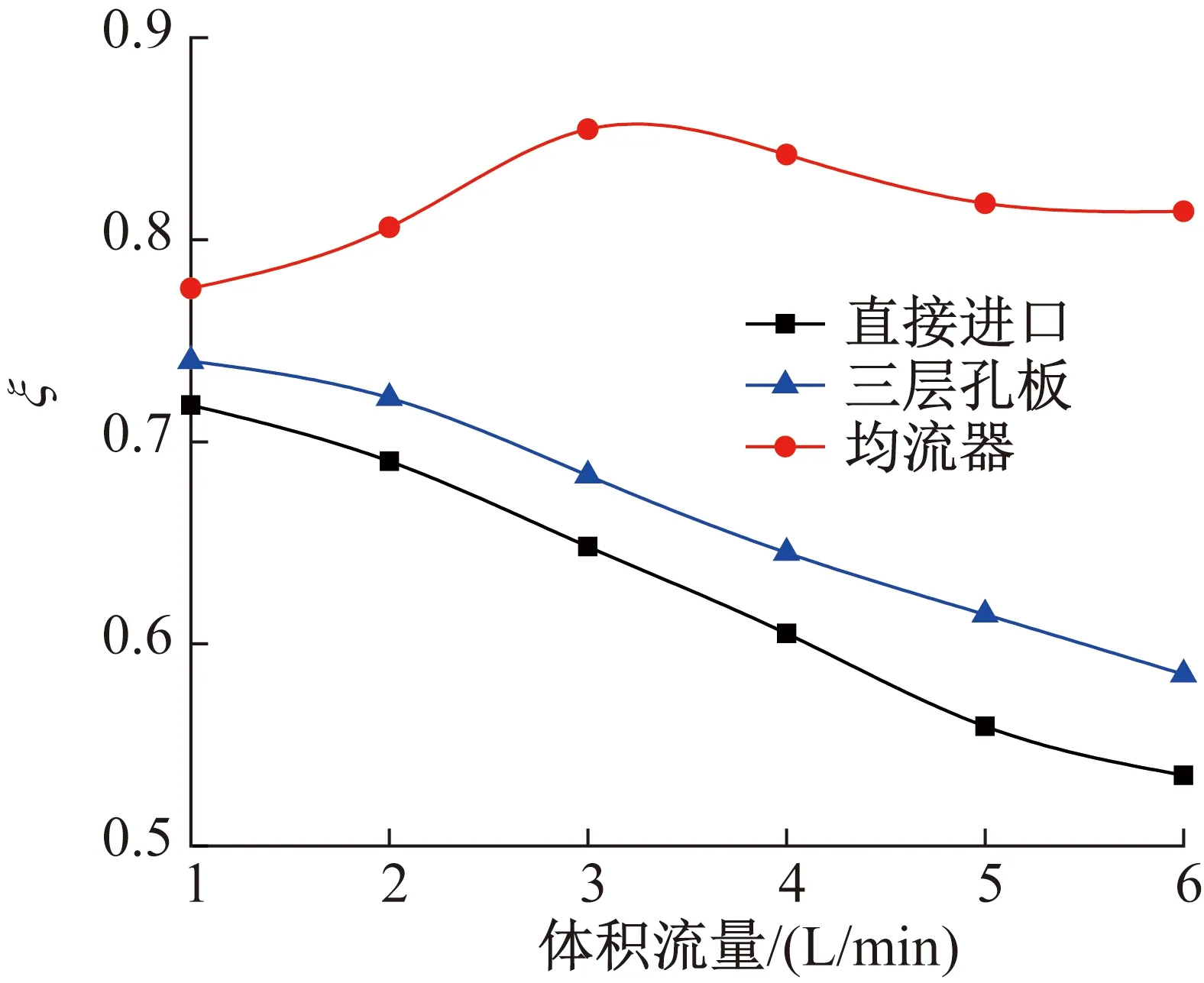
图6 填充效率随进口体积流量的变化Fig.6 The variation of the fill efficiency with inlet volume flow rates
图6所示为3种结构水箱的填充效率ξ随进口体积流量的变化。由图6可知,随着进口体积流量的增加,直接进口结构水箱和三层孔板结构水箱的ξ逐步降低。当进口体积流量为1 L/min时,直接进口结构和三层孔板结构水箱的ξ分别为0.718 27和0.740 01,相差0.021 81;而当进口体积流量为6 L/min时,ξ分别为0.534 93和0.584 93,相差0.05,说明随着体积流量的增加,直接进口结构水箱的ξ衰减较大,这主要是由于随着体积流量的增大,混合作用的加剧,直接进口结构水箱的ξ减小幅度变大,而三层孔板结构水箱由于孔板的作用减弱了水箱内冷热水混合,其ξ减小幅度较小。此外,当进口体积流量为1 L/min时,均流器结构水箱的ξ=0.775 99,并随进口体积流量的增加而增加;当进口体积流量为3 L/min时,ξ=0.854 71,达到峰值,此后,当进口体积流量增至6 L/min时,ξ减小至0.814 05。这主要是因为,当体积流量增大时,位于底部的分流器降低了进口速度,减缓了水箱内冷热水的混合,因此水箱的ξ有所提升。但随着体积流量的进一步增大,分流器对进口流量的缓冲作用减小,加剧了水箱内冷热水的混合程度,减小了水箱的ξ。当体积流量为1 L/min时,均流器结构水箱的ξ分别高于直接进口结构和三层孔板结构水箱5.7%和3.6%,并且随着体积流量的增加,ξ的增幅变大,当体积流量为6 L/min时,均流器结构水箱的ξ分别高于直接进口结构和三层孔板结构水箱27.9%和22.9%,说明在大体积流量条件下,均流器结构可以更好地提高水箱的热分层特性,进而提高水箱的效率。
4 结论
本文设计了一种用于提高蓄热水箱热分层特性的新型均流器,当初始水温为70 ℃,进水温为10 ℃,进口体积流量分别为、2、3、4、5、6 L/min工况下,与直接进口结构水箱和三层孔板结构水箱进行了热特性对比,得到如下结论:
1)不同进水结构水箱的理查德森数均随体积流量的增加而减小,三层孔板和均流器均能提高蓄热水箱的理查德森数,增强水箱的热分层特性,且均流器进水结构水箱的理查德森数最大。
2)不同进水结构水箱的混合数随放水过程的进行呈先减小后增大的趋势,表明水箱的热分层效率先提高后降低。在相同体积流量下或无量纲时间时,直接进口结构水箱、三层孔板结构水箱及均流器结构水箱的混合数依次减小,表明均流器可以更好地降低水箱内冷热水的混合程度,提高水箱的热分层效率。
3)相同进口体积流量下,直接进口结构水箱、三层孔板结构水箱及均流器结构水箱的填充效率逐步增大。直接进口结构水箱和三层孔板结构水箱的填充效率随着进口体积流量的增大而减小,且直接进口结构水箱的填充效率减小幅度大于三层孔板结构水箱,均流器结构水箱的填充效率随进口体积流量的增大而先增大后减小。此外,随着进口体积流量的增大,均流器结构水箱填充效率的增幅变大,表明在大体积流量条件下,均流器结构可以更好地提高水箱的热分层特性。
符号说明
cp——水的比热容,J/(kg·K)
D——水箱直径,m
E——水箱总能量,J
Ei——第i块水层的能量(i=1、2、3…15),J
Estratified——完美分层水箱的总能量,J
Eexp——实验水箱的总能量,J
Efully-mixed——绝对混合水箱的总能量,J
ξ——填充效率
Gr——格拉晓夫数
H——水箱高度,m
MIX——混合数
Mexp——实验水箱的能量矩,J·m
Mstratified——完美分层水箱的能量矩,J·m
Mfull-mix——完全混合水箱的能量矩,J·m

mi——每块的质量,kg
Q——水箱进水流量,m3/s
Qexp——实验水箱在τ时间内放出的能量,J·s
Qstratified——完美分层水箱在T时间内放出的能量,J·s
Ri——理查德森数
Re——雷诺数
rstratifier——水箱进水口当量半径,m
t*——无量纲时间
Ti——第i块水层的温度(i=1、2、3…15),K
Texp——实验温度,K
Thot——水箱初始水温,K
Tcold——水箱进口水温,K
Tfully-mixed——绝对混合水箱的温度,K
Ttop——水箱顶部温度,K
Tbottom——水箱底部温度,K
σ——理想活塞流情况下,将水箱内的水全部置换一遍所需时间,min
V——水箱容积,L
Vi——第i块水层的体积(i=1、2、3…15),m3
Vhot——完美分层水箱中热水的体积,m3
Vcold——完美分层水箱中冷水的体积,m3
νs——进入水箱的平均流速,m/s
yi——每个水层重心到水箱底部的垂直距离,m
ystratified——跃温层到水箱底部的垂直距离,m
ρ——水的密度,kg/m3
β——膨胀系数,1/K
τ——从放水瞬间开始所经历的时间,min

