动态制造系统生产计划与调度协同优化
王艳红 于 宁 蔡 明 邢大伟
1.沈阳工业大学管理学院,沈阳,1108702.沈阳工业大学信息科学与工程学院,沈阳,1108703.东北大学机械工程与自动化学院,沈阳,110819
0 引言
生产计划与调度是企业生产管理的核心内容,是实现制造业生产高效率、高柔性和高可靠性的关键[1]。科学的生产计划可以充分发挥企业的生产能力,充分满足市场需求;高效的调度算法可以提高生产效益和资源利用率,从而增强企业的竞争能力[2]。车间生产计划(shop production planning,SPP)主要解决生产什么、生产多少的问题,车间生产调度(shop production scheduling,SPS)则关注何时开始生产、在哪儿生产的问题[3]。随着市场竞争的加剧以及客户订单需求的多样化,传统的生产方式已难以适应现代化生产的需求,且多数企业普遍存在着“同工异地”加工方式,这使得多车间、多品种、小批量的作业模式成为主流生产方式。实际生产过程中,生产系统常会出现很多动态不确定事件(机器异常故障、紧急订单等),这势必会产生大量的扰动事件,结果将是实际生产活动永远不会与计划完全匹配,即使是再周密的生产计划都可能无法获得可行的生产调度[4]。
计划调度方案的频繁调整是为了使系统的生产计划、调度与生产活动能够产生一致性,动态制造环境的特点使得方案的调整已不能再局限于生产计划或调度之内,无论在静态规划过程,还是在动态生产过程,都应保持生产计划与调度具有较高的可靠性、耦合性和实时的协商合作能力,以便能高效地动态控制和调节系统[5]。因此对动态车间生产计划与调度协同优化的研究具有重要的意义。现阶段,很多学者针对不同的作业环境,建立了包含计划与调度的混合集成模型。张洁等[6-7]以加工时间为目标构建了调度模型;WANG等[8]为生产设置有限周期,通过定义决策变量,考虑机器的容量和客户的需求,提出了混合整数规划模型;YANG等[9]根据调度规则技术,建立了多生产线的预制生产流程调度模型;GEIGER等[10]在不确定环境下,建立生产计划与调度的数据库和规则库,进行分层优化。这类模型大多通过一些新的混合算法及分解方法进行求解,例如,WEN等[11]用一种包括随机模拟技术、神经网络和遗传算法的混合智能算法,对集成的再制造生产计划和调度系统进行优化;ZHANG等[12]采用基于模拟的优化框架来解决重制造的工作选定的过程路径优化问题;雷德明等[13]针对总能耗约束的柔性作业车间调度问题,设计了两阶段算法,提高了问题搜索能力。这些方法基本上都针对问题的特殊性构造求解。实际应用中,模型的建立往往要考虑多个相互冲突的目标,一个多目标问题可以有很多个候选解。如何选出候选解并确定一个最优的折中方案是集成优化的核心,这就需要在给出计划和调度方案的同时,对其进行优化和改进,在大多数动态制造过程中更需要对计划或调度进行重组。本文针对动态制造车间,建立了“动静联盟式”计划与调度模型,以确定动态分布环境下的生产计划情况,同时在生产计划中融合滚动调度,调度与计划形成“闭环响应模式”,用动态约束平衡的混合算法对生产计划与调度进行协同优化,并用实例验证了闭环响应下重调度的有效实施。
1 问题的描述
在动态制造环境下,为实现车间加工生产的高效性,以计划层为起点,用上层决策结果控制调度层的优化方案,再将调度层方案返回给计划层,从而建立适于批量生产的集成模型。考虑到调度目标的多样性和不确定性,在制定生产计划时,不但要考虑生产能力的约束,而且要将滚动的实时调度结果作为约束条件结合到模型中,以保证当动态问题产生时,生产计划与调度可以协同优化改变。根据调节机制,当动态情况发生时,需要根据能力约束和目标值,尽量在不改变原期望结果的情况下快速寻找最优调整策略,此时平衡机制就起到很好的作用。车间生产计划根据蚁群算法在分布状态下搜索并快速收敛从而优化。由于生产计划与调度的目标往往具有不同的属性,单目标规划往往难以达到同时优化的目的,因此采用多约束、多目标来描述生产计划与调度的优化模型更为合理。
在多品种、小批量的动态制造环境下,将生产分成T个周期,生产车间有m台设备、n个工件,工件i含k道工序,能完成每道工序加工任务的机器可能有多台,工件一旦在机器上加工就不中断。在t周期内,已知工件i的需求量dit、库存量rit。动态制造车间的首要任务是根据订单需求分解订单,根据车间生产能力Wit和库存量rit去制定动静结合的主生产计划和短期生产计划,同时考虑动静态调度调整,要求完成时间最小。
“动静联盟式”计划与调度总费用H为
H=min(γH1+θH2+μH3+ωH4)
(1)
(2)
(3)
(4)
(5)
式中,γ、θ、μ、ω为实际车间加工生产中各方面所占的权重;H1为当前协同车间批量生产的制造费用;H2为延期的惩罚费用;H3为库存费用;H4为重调度费用;T为总周期数;Xit为工件的生产量;Cit为生产费用;Fit为成本费用;pit为加工时间;Pit为惩罚费用;Rit为库存费用;sit为调整费用;Lit为重调度加工分配时间;Qit为重调度加工延迟时间;下标it表示第i个工件在第t个周期。
计划模型的约束函数考虑库存平衡约束,把生产能力和工序顺序的约束以及单机加工能力约束结合到模型中。基本的库存平衡方程为
ri(t-1)+Xit-dit=rit
(6)
同一工件不同工序间的加工顺序约束为
Eikt-Sikt≤hit+Ei(k+1)t-Si(k+1)t
(7)
式中,Eikt为在t周期工件i的第k道工序加工完成的结束时间;Sikt为在t周期工件i的第k道工序开始加工时间。
能力约束不等式为
(8)
式中,hit为调整时间。
在计划制定时,尽可能安排工件成批生产,减少准备时间,以获得设备最大利用率以保证零件的准时完工,从而达到预定的目标。
另外,对订单分解后的加工过程进行动态分析,用滚动调度来反馈控制调度和计划的形成,直至达到动态加工需求结束为止,最终使所有工件的总完工时间最小。
2 协同优化策略
2.1 闭环集成策略
集成策略是将计划与调度形成动态“闭环响应模式”。如图1所示,将能力约束加到短期生产计划及车间调度,再把调度约束与短期生产计划结合起来,把加工顺序约束与车间调度结合起来。约束后的短期生产计划与生产调度互相传递信息,形成闭环控制。所有约束用数学语言描述并放在数学模型中,在约束条件中考虑完工时间,相当于建立一个跟时间有关的目标函数,这样在动态制造生产中建立“动静联盟 (静态动态生产结合) ”的关系,通过共享信息,实现信息的双向流动,最终实现对生产系统的生产计划与调度控制。
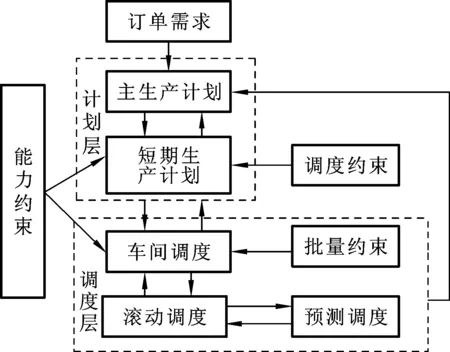
图1 集成策略Fig.1 Integration strategy
2.2 滚动重调度策略
滚动重调度策略本质上是在车间调度过程中,收集和反馈实时信息,将反馈的信息作为新的目标约束,从而对计划和调度进行调整。 动态不确定情况下,具体规则如下:
(1)需求订单改变时,在不增加库存成本的前提下,根据以往生产的预测信息,将原有信息和预测信息融合作为新的约束,调度加工在最小调整费用的前提下形成重调度方案。
(2)在订单不变的前提下,若某些工件完工时间提前或延迟,在尽量不改变最小完工时间的基础上,在调度方案中调整交换工序,形成重调度方案。
(3)加工过程中,若加工机器发生故障,则需要将未加工工件或工序调整到其他机器上完成。首先尽可能少地更改现行调度方案,根据工件加工工序的可调整方案,考虑多个约束和完成时间,控制调度方案的调整范围,以减小重调度方案带来的目标值的改变。
2.3 优化算法
遗传算法(genetic algorithm,GA)的快速全局搜索能力很强,但无法利用系统反馈的信息,导致求解效率较低。蚁群优化(ant colony optimization,ACO) 算法有较好的分布、全局收敛能力,通过累积的信息素更新,收敛于最优选择。考虑到蚁群算法和遗传算法的特点,将两者混合,应用到多车间、多品种、多批量的作业模式中,使算法整体性能得到了改善。算法的主要思路是:
(1)当订单需求发送到多车间、多机器上时,系统根据当前车间生产的能力约束,分配生产计划到机器上。在已知各工件、各工序在机器上作业所需时间和规则的基础上,将工件的加工工序作为上层染色体,将工件的加工机器作为下层染色体,最终形成双层编码的染色体,每一个双层编码的染色体对应一个调度方案,所形成的染色体为
全部工件完成时间越短,该染色体越好。种群通过交叉操作获得新的染色体,通过变异获得新的个体,实验中,遗传算法参数选取如下:选择概率Pk=0.8,交叉概率Pc=0.8,变异概率Pm=0.3。
(2)动态情况(如机器故障)一旦发生,故障机器上原本加工的工件和工序都需要调整,此时需要根据能力约束和目标值,尽量在不延长加工生产的总完成时间的基础上,快速寻找最优调整策略,平衡机制就起到了很好的作用,通过改变信息素增量的大小,使蚁群算法能在分布状态下快速搜索并收敛。在实验中,蚁群算法参数选取如下:循环次数N=100,蚂蚁数量λ=100,信息素增量Q=100,信息素启发因子α=1.5,期望启发式因子β=5,信息素剩余量系数ρ=0.6。
因此本文采用混合遗传蚁群算法,用遗传算法判断是否满足终止条件,进一步判断是否达到融合条件,并针对蚁群算法的挥发系数加入动态调整策略。蚁群算法使用的转移规则(随机比例规则)定义了蚂蚁位于节点工件i经过第m次运动时运行到节点工件j的转移概率Pijm。根据算法的局部最优倾向程度来动态调整挥发系数,从而避免算法早熟和局部停滞,其动态调整机制如图2所示。
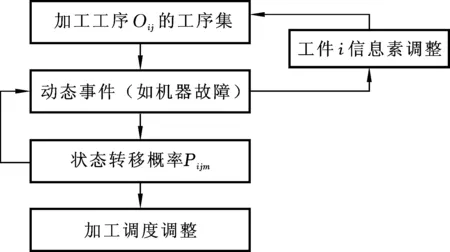
图2 动态调整机制策略Fig.2 Dynamic adjustment mechanism strategy
3 仿真研究与分析
3.1 仿真算例
假定订单有6个工件、4台机床,每个工件有4道工序,且这些工件必须按照规则进行加工,各工件、各工序在机器Mi上所需作业时间如表1所示,考虑到动态加工包含多个方面的情况,这里为了简化问题,将各费用所占权重设为1,只考虑动态加工下的机器故障问题。
表1各工件各工序所需作业时间表
Tab.1Timetablerequiredfortheworkofeachworkpiece
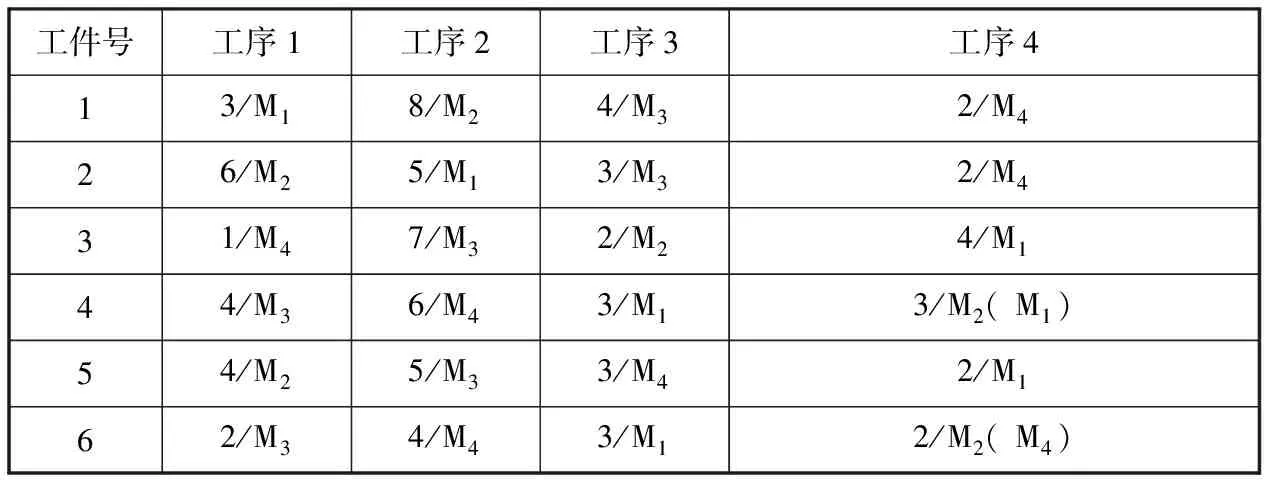
工件号工序1工序2工序3工序413/M18/M24/M32/M426/M25/M13/M32/M431/M47/M32/M24/M144/M36/M43/M13/M2( M1)54/M25/M33/M42/M162/M34/M43/M12/M2( M4)
注:x/Mi表示第i台加工机器的加工时间为x,h;括号内的是备选加工机器。
3.2 静态优化仿真
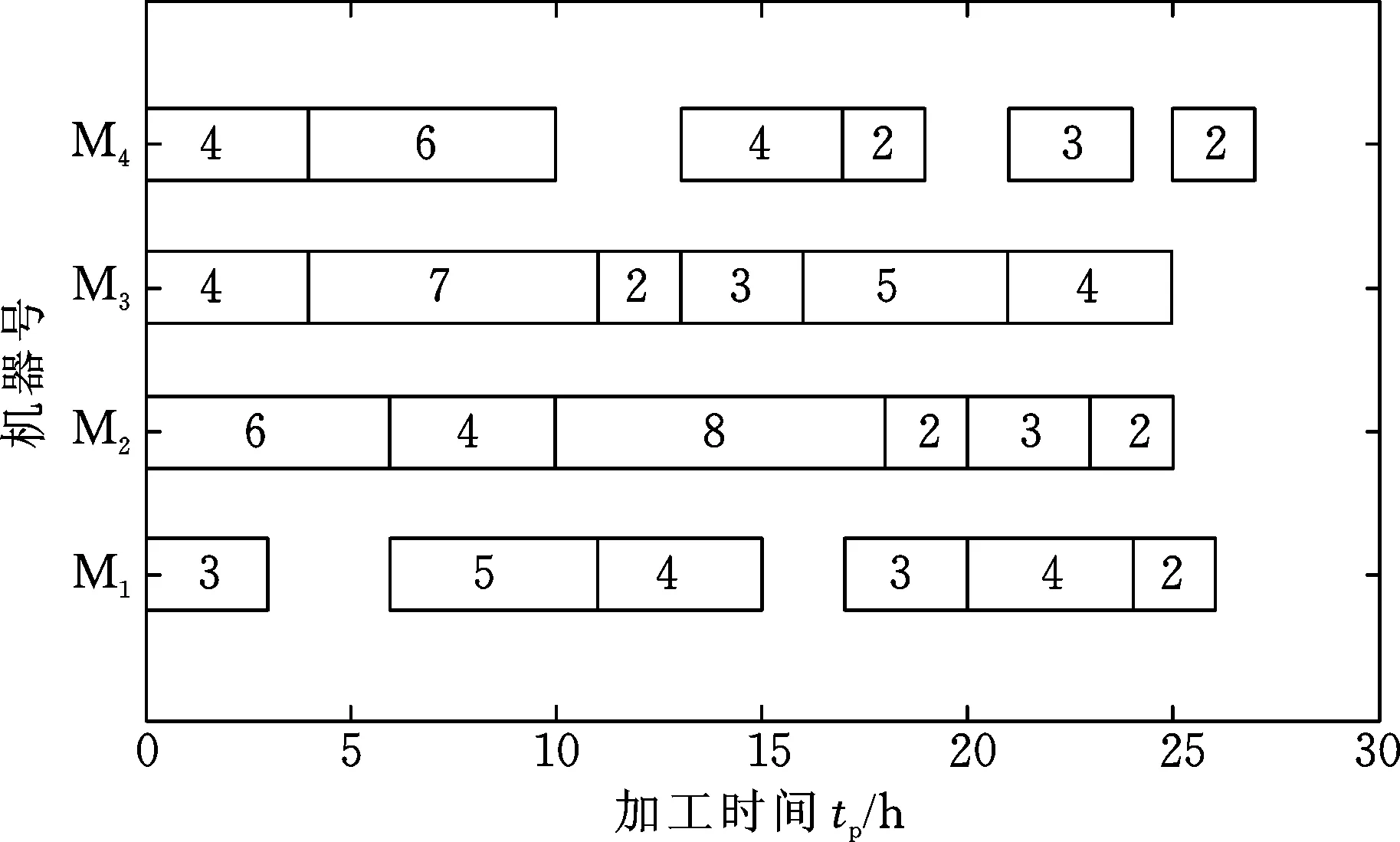
图3 加工甘特图Fig.3 Processing Gantt chart
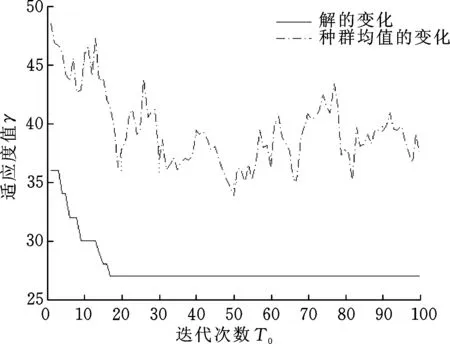
图4 收敛曲线Fig.4 Convergent curve
为了验证所提出算法的有效性和优越性,用基准数据作为测试例,将蚁群算法与遗传算法的混合算法(下文简称混合算法)同遗传算法进行对比,结果如表2所示。
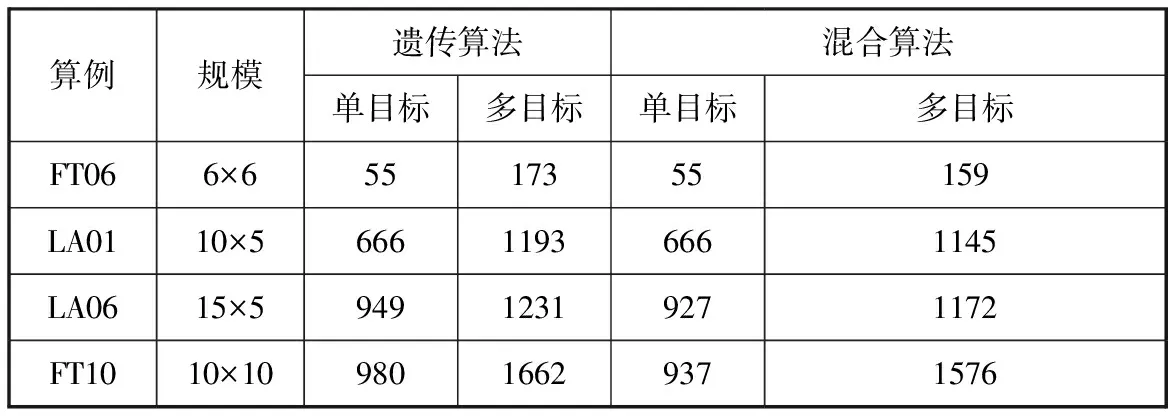
表2 基准数据测试仿真结果对比
同时在同一标准参数下对同种情况进行多次仿真,得到了最优解和最优解均值,见表3。
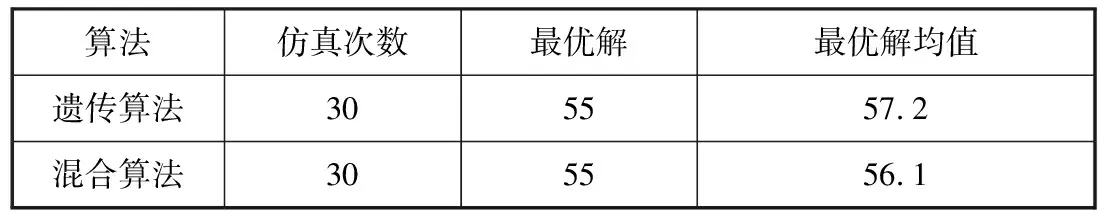
表3 运行结果对比
3.3 动态优化仿真
为验证动态环境下重调度的可行性,假设加工进行到某一时刻,机器发生故障,动态控制平衡机制会在故障点,根据滚动调度传达动态实时加工信息,以在不改变最小加工时间的情况下减少总费用,重新进行计划信息调整和调度重组。图5为机器2在某一时刻发生故障时,加工信息和调度重新调整重组的甘特图。
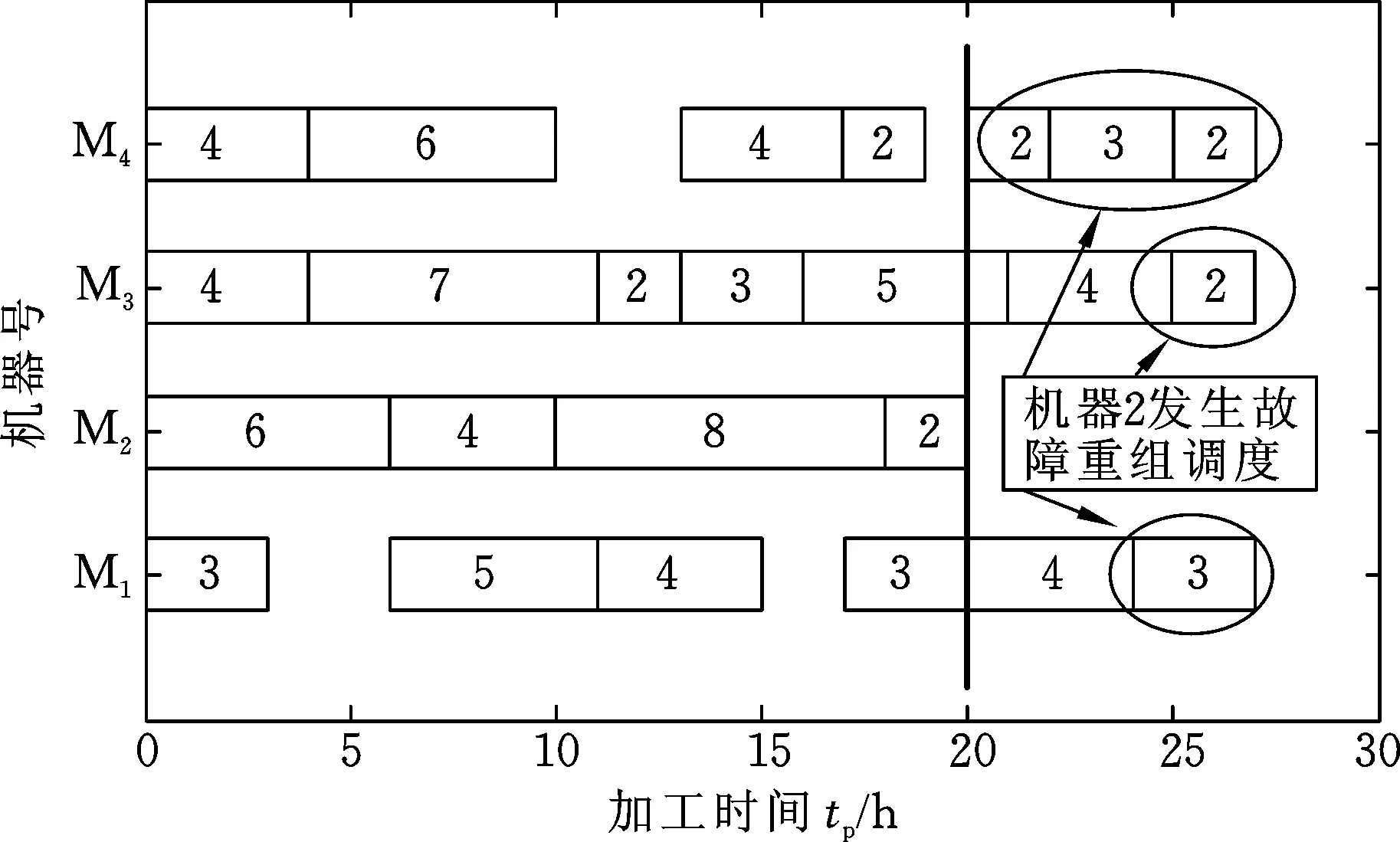
图5 故障发生后调度重组的甘特图Fig.5 Gantt chart of scheduling reconfiguration after failure
4 结论
(1)针对动态车间的生产计划与调度问题,建立了一种“联盟协作”模型,可根据实际生产模式设置不同需求费用所占权重。
(2)在集成策略上设计了计划与调度互相传递信息的闭环响应模式,并提出滚动调度和预测调度相结合的策略,使加工计划与调度能根据返回的有效动态信息进行更改,避免频繁调整。
(3)通过实例仿真,对计划与调度策略进行分析,并对某一时刻机器故障对系统调整的影响进行验证,得出重调度策略的计算时间和仿真结果。
(4)通过用不同算法对基准算例进行仿真,在不同目标情况下进行对比,验证了所提出算法的有效性和优越性。

