并行多机开放车间调度问题的模型与算法

陈亚绒 黄佩钰 李 沛 周富得 黄沈权

温州大学机电工程学院，温州，325035

0 引言

开放车间调度问题(open shop scheduling problem，OSSP)一般描述为将有限集合J={j1，j2，…，jn}中的n个工件安排在车间的s个阶段(或道次)的机器上加工，k阶段机器的数量为mk(k=1，2，…，s)。每个工件都包含s道工序，每道工序在每台机器上的加工时间确定。在给定的时间内，每台机器只能加工一个工件，且每个工件只能由一台机器加工。同一台机器上工件的加工顺序任意，每个工件的加工顺序也无限制。若k阶段机器的数量mk=1，则这类调度问题称为传统开放车间调度问题；若mk≥1且s≥2，同时每个阶段的机器为同类等效机，则此类问题称为并行多机OSSP[1-3]。

晶粒分类拣选工序是发光二极管(light emitting diode，LED)制造过程中的关键工序，该工序的生产调度问题是典型的并行多机OSSP，其调度算法是否有效直接影响LED制造工厂的生产[4]。

开放车间调度问题具有NP-hard属性[5]，因此许多学者开发启发式算法[6-7]以及智能优化算法如遗传算法[8-10]、蚁群算法[11]与粒子群算法[12-13]，以期在较短的时间内得到近似最优解。考虑到现实生产的动态与随机性，采用仿真方法的研究日益受到关注。如文献[14]研究了一种基于仿真的实时调度方法，来优化释放时间随机的非抢占开放车间调度问题。研究的调度目标主要是最小化Makespan或总完工时间[7-8，10-12]、最小化平均流程时间[6]、最小化总拖期[9]。比较而言，有关并行多机OSSP的研究相对较少，BAI等[15]研究了基于GDS求解大规模OSSP的启发式算法，以及求解中等规模OSSP的差分进化算法；针对实际问题中工件批量大于1的需求，WANG等[16]提出了分割求解工件批量的并行多机OSSP的差分进化算法；MATTA[17]提出了一种求解并行多机OSSP的计算机搜索方法；CHEN等[18]研究了每个阶段两台机器的OSSP，提出了求解该问题的多项式时间近似算法。文献[19]提出了一种基于网络流求解并行多机可中断OSSP的调度算法。这些文献的调度目标均是完工时间最小化。以当前的研究文献为基础，结合晶粒分类拣选工序的生产特性分析，本文以最小化总加权完工时间为目标，构建了并行多机OSSP的混合整数规划模型，设计了可以快速有效获得较佳解的启发式算法及改进粒子群优化算法，并通过实验仿真比较了不同算法的绩效。

1 晶粒分类拣选工序的调度问题描述

调研LED制造工厂得知，根据客户标准，晶圆片上的每一颗晶粒都可以归类到128种晶粒等级中的一种。每一台晶粒分类拣选设备/机台最多只能分类32种等级的晶粒。已设定分类某些等级晶粒的设备更改为其他等级时，需耗费8h的程序设定时间。实际生产过程中，管理者一般依照经验将128种晶粒等级归类成4～8群，每个群最多包含32种特定的晶粒等级；然后将若干台分类拣选设备设定成专门分类拣选“专属群”的晶粒等级。每一片晶圆都要历经4道以上不同“专属群”的加工工序(没有先后限制)，每道工序的加工设备是多台同类平行设备(图1)，因此该调度问题是典型的并行多机开放车间调度问题O(Pm1，Pm2，…，Pms)/rj/Σwjcj。

图1 晶粒分类拣选工序加工示意图Fig.1 Schematic diagram of grain sorting process

根据上述的生产作业环境，本文探讨的晶粒分类拣选工序生产调度问题描述如下：①磊晶工序之后的每一片晶圆都是一个独立的工件；②经过电性与旋光性针测工序，晶圆j上的晶粒等级、位置与数量确定且已知；③晶圆j释放(或抵达)到晶粒分类拣选工序的时间为rj；④晶圆j要经过s道晶粒分类拣选设备的加工(没有先后限制)，工序k包含mk台同型设备；⑤每台设备从晶圆片上拣选1颗晶粒所需的时间确定且已知；⑥每片晶圆在工序k上的作业时间等于这道工序设备拣选的晶粒总数量与拣选1颗晶粒所需时间的乘积；⑦每台晶粒分类拣选设备一次最多只能分拣1片晶圆，且不允许抢占；⑧调度期间内，不考虑晶粒分类拣选设备发生故障停机的情形；⑨晶圆j的经营管理绩效重要程度即权重确定且已知；⑩生产绩效是最小化总加权完工时间。

2 晶粒分类拣选调度问题的混合整数规划模型

针对晶粒分类拣选工序的并行多机、加工工序没有先后限制的生产特性，构建了求解此类调度问题的混合整数规划(mixed integer programming，MIP)模型。

晶粒分类拣选工序调度问题MIP模型的目标是最小化所有工件的总加权完工时间。

最小化总加权完工时间为

(1)

式中，wj为工件j的权重系数；Fj为工件j的完工时间；n为晶圆或工件数量。

约束条件如下：

(1)每个工件在各个道次间执行的先后顺序关系为

(2)

(3)

(2)一个工件的一个道次中只允许在该道次的多台并行机台中的一台机器上加工，即有

(4)

(5)

(3)每个工件在每个道次中的完工时间必须不小于此工件的释放时间与此道次加工时间之和，即

(6)

式中，Cjk为工件j在道次k的完工时间；rj为工件j的释放时间；pjk为工件j在道次k的加工时间。

(4)每个工件最终的完工时间必须不小于此工件在每个道次的完工时间，即

Fj≥Cjk

(7)

(5)每个工件在任意两个道次间的完工时间必须满足先后顺序关系，该先后顺序关系的数学表述为

(8)

式中，M为很大的正整数；Cjl为工件l的工序完工时间。

(6)任意两个工件在同一道次的同一台机器上加工时，必定有先后顺序的关系；反之，则没有先后顺序的关系，该先后顺序关系的数学表述为

(9)

(10)

(7)任意两个工件在同一道次的同一台机器上同时加工，两个工件之间的完工时间必须满足先后顺序关系，该先后顺序关系的数学表述为

(11)

晶粒分类拣选工序的生产调度问题属于NP-hard问题，建立的MIP模型主要用于验证后续设计的启发式算法与改进粒子群优化算法结果的正确性，并将MIP模型求得的解作为评估调度算法求解质量的基准。

3 晶粒分类拣选调度问题的启发式算法

尽管MIP模型可以求解晶粒分类拣选工序的生产调度问题，但当工件数量或晶粒分类拣选机器的数量急剧扩大时，MIP模型无法在可接受的时间内获得最优解，甚至无法获得任何一组可行解。考虑求解效率与现实运作要求，有必要设计迅速且有效获得满意可行调度解的启发式算法。

本文提出的启发式算法将整个求解过程细分成多个阶段，每个阶段只针对一台晶粒分类拣选机器与一个工件进行指派。阶段与阶段之间相互关联，即k+1阶段的求解是在k阶段获得的可行解基础上进行的，具体执行步骤如下：

(0)令时间初始值t←0。

(1)从所有晶粒分类拣选机器中找出还有工件需要加工的机器，将每台满足机器可用时间ma≤t的晶粒分类拣选机器放到候选晶粒分类拣选机器集合。

(2)若候选晶粒分类拣选机器集合为空集，则令t←t+1，执行步骤(1)；否则，根据晶粒分类拣选机器的优先处理规则，从此候选晶粒分类拣选机器集合中选择晶粒分类拣选机器。

(3)筛选所有还需要在步骤(2)选择的晶粒分类拣选机器上加工处理的工件，将每个满足工件释放时间wr≤t的工件纳入到候选工件集合之中。

(4)若候选工件集合为空集，则令t←t+1，执行步骤(1)；否则，根据工件的优先处理规则，从此候选工件集合中选择工件。

(5)更新此阶段晶粒分类拣选机器的可用时间ma、工件的释放时间wr。

(6)若尚有工件未指派处理完成，则返回执行步骤(1)；否则计算目标函数值，结束启发式算法。

晶粒分类拣选机器的优先处理规则是“未来剩余工件的平均负荷大者优先指派”。若晶粒分类拣选机器的平均负荷相同，则机器序号小者优先。工件的优先处理规则是“pj/wj小者优先指派”。若某道次工序当中的pj/wj相同，则工件序号小者优先指派。

4 晶粒分类拣选调度问题的改进粒子群优化算法

改进粒子群优化(modified particle swarm optimization，MPSO) 算法的基本概念与传统PSO相同，只在运行机制上进行了改进。

4.1 编码

传统PSO算法主要适用于求解连续空间域的优化问题。针对晶粒分类拣选调度问题的离散空间域组合优化问题特征，本文采用随机数大小顺序值排列(rank order value，ROV)编码方式，将连续空间域的粒子位置映像转换为离散空间域的调度解粒子[20]。

(1)对每个粒子使用ROV方法，将连续空间域的粒子位置映像转换成离散空间域编码。

(2)针对经过ROV映像转换后的每个粒子，利用Hash函数来计算此粒子的类似索引码，通过此数值来判断2个粒子的离散空间域编码是否重复。

(3)若粒子的离散空间域编码重复，则基于粒子多样性的需求，运用随机数重新产生一个粒子来取代此粒子。

4.2 解码

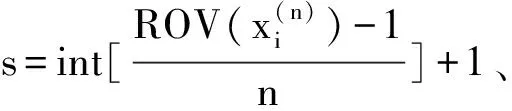
4.3 算法运行机制

MPSO算法运行机制的伪代码如下。

Initialize parameters ofNp，δ，c1，c2，reduce_rate，andtime_limit

Generate initial positionXi(0) and velocityVi(0) for particlei，∀i=1,2,…,Np

SetPi(0)=Xi(0)，Gb(0)=X1(0)，Gw(0)=X1(0)，timer=0，t=0

Do

Fori=1 toNp// 计算粒子群内每一个粒子的位置Pi(t)

IfZ(Xi(t))≤Z(Pi(t)) then

Pi(t)=Xi(t)

End if

Nexti

best= 1，worst= 1 //找出当前粒子群中最好与最差的位置Gb(t)，Gw(t)

Fori=1 toNp

IfZ(Xi(t))≤Z(Pbest(t)) then

best=i

End if

IfZ(Xi(t))≥Z(Pworst(t)) then

worst=i

End if

Nexti

IfZ(Pbest(t))

Gb(t)= Pbest(t)

Local_search(Gb(t)) //两两交换局部搜寻

End if

IfZ(Pworst(t))>Z(Gw(t)) then // 淘汰群内最差的粒子

Gw(t)=Pworst(t)

If random number≤threshold then

Generate a new particle randomly

ReplacePworst(t)，Xworst(t)，Vworst(t)

End if

End if

Fori=1 toNp// 更新每一个粒子的速度与位置

Vi(t+1)=δ·Vi(t)+c1·r1·(Pi(t)-Xi(t))+c2·r2·(Gb(t)-Xi(t))，Vi(t+1)∈[Vmin，Vmax],

Xi(t+1)=Xi(t)+Vi(t+1)，Xi(t+1)∈[Xmin，Xmax]

Nexti

Similarity check for a couple of particles

If similarity check is true，then

Generate a new particle randomly and replace one of the particles by the new one

End if

t=t+1，δ=δ×reduce_rate，δ∈[δmin，δmax]，updatetimer

While (timer≤time_limit)

除编码与解码之外，MPSO算法与传统PSO算法的不同之处如下：

(1)用惯性权重来控制粒子群优化搜索过程中整体探索与局部探索的比重。初期着重于整体性探索，惯性权重比较大；随着运行时间的增加，搜索偏重于局部性探索，则惯性权重逐步减小。

(2)执行一次迭代后，为了增加群体多样性，将当前目标函数值最差的粒子淘汰，然后随机产生一个新的粒子来替代。

(3)为了增加搜索的有效性，假使当前目标函数值最好的粒子改变时，借由两两对调局部搜索(pairwise interchange local search)机制来加以辅助运行，改善搜索的有效性。

5 仿真实验与分析

5.1 实验数据生成

5.2 实验结果分析

采用求解质量偏差百分比PD=(A-O)/O来评估不同算法的求解质量，其中，A为算法求得的解，O为评估基准值。当工件数量较小时，O为MIP获得的最优解。当工件数量较大时，MIP无法在2 h内获得最优解，O为2 h内取得的上界值BU与下界值BL，实际的PD在根据BU与BL计算得到的PD之间。

5.2.1各种实验参数之下四种算法的绩效比较

通过初步分析实验结果发现，当工件数量n处于一定范围时，算法的绩效相似，因此将其分成3个区间进行分析。MIP法、启发式算法、MPSO算法与传统PSO算法在各种实验参数之下的绩效如表1所示。绩效用解目标值R与运行时间T表示。工件数量n增大时，MIP法无法在最大可接受时间内获得最优解，其解目标值细分为BU与BL。

由表1可知，对于pjk、mk、rj的不同组合，当求解问题的规模较小(n≤5)时，MIP法、MPSO算法、传统PSO算法与启发式算法均能获得问题的最优解或近优解。问题规模较大(5

5.2.2求解质量分析

不同加工处理作业时间pjk、k次工序所配备的机器数量mk、工件数量n以及工件的释放时间rj等参数组合之下，启发式算法、MPSO算法与传统PSO算法的求解质量偏差PD如表2所示。

表1 4种算法在不同参数组合下的绩效汇总表

表2 不同参数组合下3种算法的求解质量偏差PD

注：括号里面的值代表PD为负值，表示该算法的解比MIP法在2 h可接受时间内获得的最好解更接近最优解。

由表2所示的结果可知，MPSO算法、传统PSO算法与启发式算法的求解质量偏差PD不仅与工件数量有关，也受pjk、mk与rj的影响。对于pjk、mk、rj的不同组合，随着求解问题规模的变大，3种算法BU的求解质量偏差PD基本呈现由小(PD=0)到大再到更小(PD<0)的趋势，BL的PD呈现由小到大的变化趋势。这表明当求解问题的规模足够大(n≥11)时，3种算法获得的解优于或接近在可接受时间内MIP法获得的最优解，且求解问题的规模越大，求解质量偏差PD的优势越明显。其中，MPSO算法的求解质量优于传统PSO算法，传统PSO算法的求解质量优于启发式算法。原因在于，求解问题规模的变大导致可行解空间的增大，进而造成MIP法在最大可接受时间获得的最好解与最优解的偏差变大。

5.2.3实验参数的影响分析

为比较实验参数对启发式算法、MPSO算法与传统PSO算法的影响，统一将加工处理作业时间pjk(U[1,10]与U[1,20])、k道次工序所配备的机器数量mk(U[1,3]与U[1,5])以及工件的释放时间rj(U[0,25]与U[0,75])的两个水平取值分别标记为-1与-2。3种算法在pjk、mk与rj等参数不同取值之下的PD如图2～图4所示。

图2 pjk对3种算法PD影响Fig.2 Influence of pjk on PD of three algorithms

图3 mk对3种算法PD影响Fig.3 Influence of mk on PD of three algorithms

图4 rj对3种算法PD影响Fig.4 Influence of rj on PD of three algorithms

由图2～图4可知，实验参数pjk、mk与rj对启发式算法PD的影响大于MPSO算法和传统PSO算法。问题的规模n=11时，实验参数的取值对MPSO算法和传统PSO算法的PD几乎没影响，图2～图4中显示为几乎重合的数据点。根据PD的计算方法可知，若调度问题的复杂度或难度变高，MIP法很难在可接受的时间内获得最优解，其他3种算法的BU的PD会变小，BL的PD会变大。因此，总体上实验参数对算法的影响如下：pjk=U[1,20]的BU的PD优于pjk=U[1,10]的BU的PD，而pjk=U[1,20]的BL的PD劣于pjk=U[1,10]的BL的PD；mk=U[1,3]的BU的PD优于mk=U[1,5]的BU的PD，而mk=U[1,3]的BL的PD劣于mk=U[1,5]的BL的PD；rj=U[0,25]的BU的PD优于rj=U[0,75]的BU的PD，而rj=U[0,25]的BL的PD劣于rj=U[0,75]的BL的PD。需要注意的是，实验参数对启发式算法BU的PD的影响与MPSO算法和传统PSO算法有所不同，在问题规模变大(n≥15)时发生了转变。原因是实验参数取值对启发式算法求解质量的影响大于问题规模的影响。总之，当问题规模较大(n>11)时，3种实验参数变化之下：MPSO算法的PD变化范围小于传统PSO算法，传统PSO算法的PD变化范围小于启发式算法，这表明MPSO算法的稳健性最高。

6 结语

本文针对LED制造工厂的晶粒分类拣选调度问题的并行多机生产特性，建立了求解此类调度问题的混合整数规划模型，兼顾求解效率与质量，设计了一种简单易行的启发式算法和一种改进粒子群优化算法。根据企业的生产实践设计了实验算例，通过比较4种算法的调度绩效，发现启发式算法虽能快速求解，但是求解的质量仍然有改善的空间，改进粒子群优化算法在求解速度与质量的要求下均能满足企业晶粒分类拣选调度的实务要求。同时，对于加工处理时间、释放时间以及每一道次工序所配备的机器数量等参数的变化，改进粒子群优化算法的变化范围最小、最稳健。未来研究方向将侧重于考虑将改进粒子群优化算法用于其他的调度问题，以及探讨晶粒分类拣选工序的生产调度问题的多目标优化求解方法。