闸门振动监测与ELM预测模型研究

汤小飞

(江苏省泰州引江河管理处，江苏 泰州 225321)

我国高水头水利工程建设规模已跃居世界第一。水头的逐渐提高对闸门的要求也日益提高，对闸门的灵活性、安全性和耐久性都有了极高的要求[1- 2]。在水利工程中的闸门，分为平板闸门、弧形闸门、人字闸门、圆通闸门等，用的最多的为平板闸门和弧形闸门[3]。弧形闸门具有受力合理、质量可靠、启动迅速等优点，但存在着不便检修、造价较高、占地空间大的缺点[4]。平板闸门由于其占地空间小、运行建设方便、便于检修等优点，同样应用广泛[5]，直升式平板闸门为平板闸门中应用最广泛的型式[6]为本文的研究对象。

闸门作为水工建筑物中的主要挡水设施，其稳定性决定着水利枢纽的运行寿命与安全，闸门的失稳直接威胁水工建筑物的安全，直接影响着居民的人身安全[7]。由于闸门上下游水位的不断变化，同时受到水跃、冰压力等作用的影响，闸门易受到脉动压力的影响，从而引起闸门振动，造成闸门裂缝，引发闸门失稳[8]。现有的研究基本集中在对闸门振动的原型观测和数值模拟中[9- 10]，对闸门振动的预测模型研究较少。本文通过原型监测试验得出试验数据，并基于ELM预测模型对闸门振动进行预测，以期为闸门设计与安全运行提供理论依据。

1 试验观测与研究方法

1.1 闸门振动试验观测

对于闸门的振动监测，针对平板闸门主要受力部位主梁和纵向隔板的监测，如图1所示共设置40个振动监测点。在设计水位下，闸门所受振动压力随着部位的不同呈现不同的分布特征，监测闸门启闭过程中，其振动脉动压力与位移变化，从而得出长序列数据，为闸门安全运行评价与预测模型建立提供数据支撑。

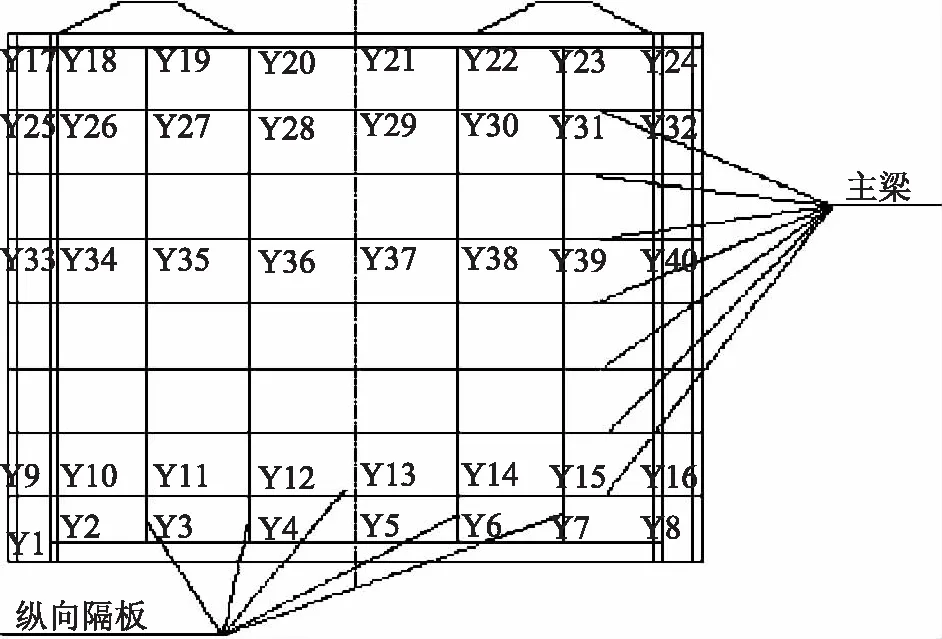
图1 闸门测试点分布图

1.2 闸门振动ELM预测模型建立

传统的神经网络模型存在训练速度慢、易陷入局部最优等缺点。ELM模型可以很好地克服这些缺点。其具有收敛速度快、计算精度高等优点，在回归检验、模型预测领域已得到了极大的应用[11]。图2为ELM模型的基本原理图，ELM模型主要可分为输入层、隐含层和输出层3部分。首先通过输入层输入所求变量，通过与隐含层之间的权重ωij，计算出输出层权重βjk和输出变量矩阵，得出最终结果。

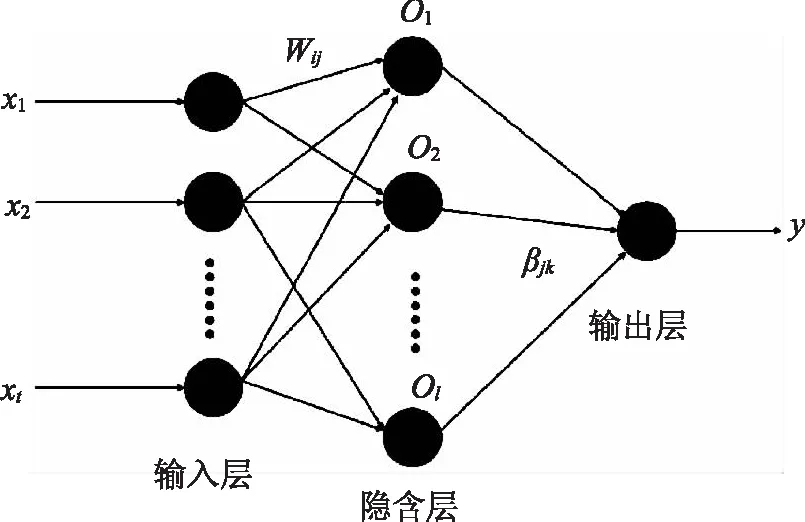
图2 ELM模型计算原理图

极限学习算法将神经网络输出权重过程分为2步。在初始阶段，假定所求权重为β，假设初始输入权重为ai和输入偏置bi，输入层矩阵用H0表示，通过式(1)计算输出权重β0为:

(1)

(2)

式中，β0—输出权重；H0—输入层矩阵；T0—变量矩阵。

对于输出权重βi，可由下式计算：

(3)

(4)

根据求得的输出权重，与输出变量进行运算，最终求得极限学习机算法的最终模拟结果。

本文中ELM模型算法采用Matlab2013a软件进行模拟计算，详细运算过程与代码形式见参考文献[12]。

1.3 预测模型精度指标体系建立

Nash-Sutcliffe系数(CD)、逐日相对均方根误差(RMSE)和决定系数(R2)可以较好地反映长时间预测序列与实测值的误差和一致性，是系统性较好的数据评价指标体系。其中，CD与R2的值越大、RMSE的值越小，模型算法与实测值的一致性越好、计算精度越高，RMSE和CD具体公式如下，R2采用EXCEL表计算取得：

(5)

(6)

2 结果与分析

2.1 闸门水流脉动压力观测

图3为闸门脉动压力随时间及闸门开度的变化过程。图3显示，闸门所受压力随着闸门开度的增大而增大，在试验原型监测过程中可以发现，试验测得的最大脉动压力出现在闸门开度为8.0m时，之后随着闸门开度的增大，闸门所受脉动压力有所降低，最大脉动压力均方根值达到了1.16m水柱，按3倍均方根值估计最大值，则最大脉动压力约为3.48m水柱。

由闸门典型测点的脉动压力功率谱密度曲线可知，闸门所受的脉动水压力在5s和15s左右时为正值，其余基本为负值，表明闸门承受的主要能量来自于5s和15s左右的范围内。

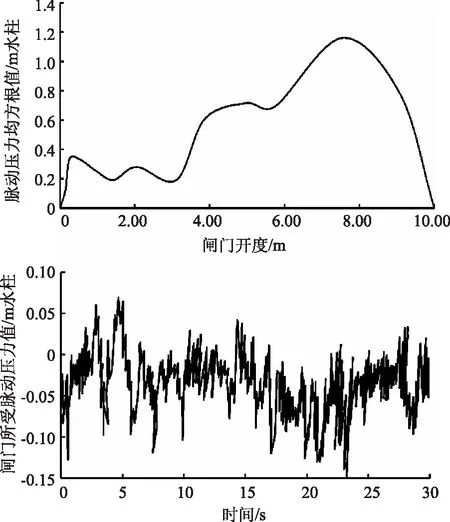
图3 闸门脉动压力变化过程监测

2.2 闸门振动响应监测

图4为闸门振动位移与加速度随时间的变化过程。图4显示，闸门振动位移的频率较低，主频为5～10Hz，加速度的频率较高，频带较宽，主频达到了20～30Hz，同时闸门振动位移在20s左右达到最高值，为1.547mm，加速度在15～20s附近达到最高值，已有研究表明平均振动位移为0～0.0508mm时可忽略不计，在0.0508～0.2540mm之间为微小振动，在0.2540～0.5080mm之间为中等振动，大于0.5080mm为严重振动[13]，本研究在监测闸门振动时，发现闸门振动的平均振动位移为1.36mm，属于严重振动，因此，该闸门的振动安全存在隐患，应优化闸门结构，采取措施增强闸门结构的整体性，提高结构的刚度和自振频率，以减小其振动响应。

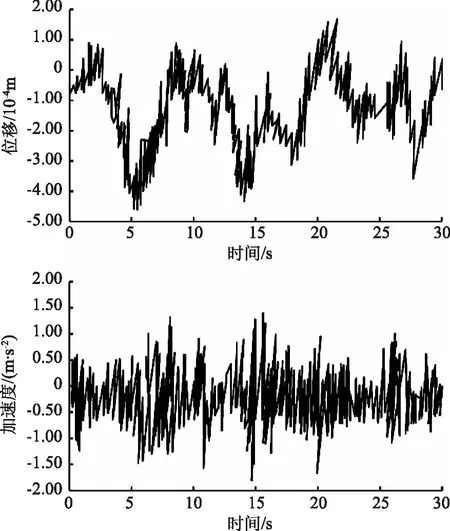
图4 闸门振动响应时程分析

2.3 ELM模型预测结果分析

图5为ELM模型预测值的脉动压力与实测值的对比。图5显示，按0～15s的数据训练模型，验证15～30s的数据，模拟出的数据与实测值的拟合效果较好，模拟值同样在5s和15s左右时为正值，同时对模拟值进行精度指标检验可知，模拟值与实测值的RMSE值仅为0.207，而CD与R2分别达到了0.824和0.898，且与实测值的相关性达到了极显著水平(P<0.01)，表明预测模型结果表现出了较高的一致性与较低的误差，可充分反映该模型的预测精度，该模型可作为闸门振动预测的模型使用。

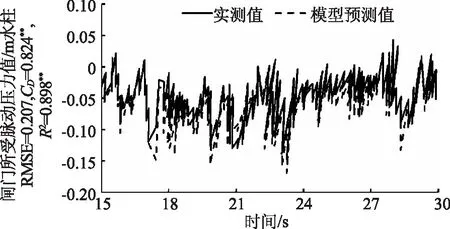
图5 预测模型模拟结果与实测值对比

3 结论

(1)闸门所受压力随着闸门开度的增大而增大，闸门开度为8.0m时，所受压力达到最大值，闸门所受的脉动水压力在5s和15s左右时为正值，其余基本为负值，表明闸门承受的主要能量来自于5s和15s左右的范围内；

(2)监测过程中发现，闸门振动的平均振动位移为1.36mm，属于严重振动，应及时采取措施；

(3)对闸门脉动压力进行ELM预测可知，预测结果与实测值的RMSE值仅为0.207，而CD与R2分别达到了0.824和0.898，精度较高，可作为闸门振动监测的标准预测模型使用。