基于政府间博弈的农村饮水安全工程补偿分摊模型研究
张 艳
(铁岭市铁岭县水利局,辽宁 铁岭 112600)
农村饮水安全工程是一项公益性系统工程,其本质是对农村居民生活饮用水水质不洁、供水保证率低、取水困难、水量不足等状况进行改善,政府补偿在很大程度上决定了其运行效率的高低[1]。当前,省级政府和中央政府承担了约80%的农村饮水安全工程的建设资金,基层政府承担了约20%的资金。而补偿费用在项目运行阶段则完全由基层政府承担,财权和事权在项目运行阶段分别向中央上移与地方政府下放是造成政府无力承担项目各项支出费用的关键性因素。因此,基层政府为减少财政支出对饮水安全工程项目的补偿费用往往希望省级政府和中央分担。而基层政府与省级政府在向中央与省级政府上报分担补偿费用时会产生各级政府间补偿分担比例虚报等问题[2]。董文虎等[4]依据水利工程消耗补偿基本状况给出了公益性资产与经营性资产的补偿标准和分类;何寿奎等[5]在分析了水利工程在国内外常用补偿模式,对影响私人投资者参与和维护水利工程建设积极性的因素开展了科学研究。工程消耗的补偿原则、补偿办法以及补偿模式等方面为当前研究的主要内容和方向,涉及补偿分担等问题的研究相对较小。据此,薛小杰等[6]通过对效益分摊影响因素进行研究建立了补偿分摊模型,并给出了补偿效益在不同条件下合理的分摊方法;高士春等[7]利用熵权法构建了效益补偿分摊模式并以大渡河阶梯电站为研究对象进行了各种分摊模式的研究,研究成果可为流域效益补偿提供决策依据和支持;李维乾等[8]通过对上下游流域的DEA合作博弈进行分析,给出了研究流域的分摊补偿方案并为该区域提供了一定决策依据;上述相关研究主要是对补偿效益分摊进行研究,而对补偿主体的分摊问题并未展开深入的研究。据此,本文针对补偿资金的虚报问题讨论了省级与中央政府参与补偿的费用分摊研究,并为降低省级政府发生虚报的可能性构建了中央与省级政府的监督博弈模型,所构建的分摊比例模型可为各级政府间的补偿分摊提供决策依据和支持。
1 构建模型
1.1 各级政府申报与监管博弈模型
考虑到人的思维局限性、信息不完全以及环境复杂等因素影响并为研究方便,在建立博弈模型前需做基本的假设,即假定基础、省级以及中央政府三级补偿主体在追求自身利益最大化时均认定为具有合理性。由于中央和地方政府在农村饮水安全工程项目运行补偿分摊问题上不同的目标,可将其作为一个信息动态不完全的博弈,地方政府补偿作为中央政府的依托完成项目运行。中央政府和地方政府分别为委托人和代理人,而地方政府在委托人对代理人监管不力时可增大其财政缺口并产生农户对水的有效需求夸大的现象。中央政府在财政收入保持不变的条件下可通过对地方政府的监管降低补贴成本。中央政府考虑到地方政府可能发生的虚报补偿的情况,需对其进行监管然而无法对每个、每次案例进行监管。地方与中央政府在监管与申报博弈过程中可存在虚报与不虚报以及监管和不监管等策略选择。因此在进行不同策略选择时可对如下变量进行确定:区域省份的实际需求和省政府的申报需求分别以R、D进行表征;总虚报资金以及省政府的努力程度采用F、W表征;中央政府的补偿投资和建设投资分别利用C、B表征;省级政府的实报概率和中亚对提防政府虚报行为的监管成分分别利用r、I进行表征;非负参数分别为α、θ;选择监管的概率利用p表示。
依据省级与中央政府设定的申报与监管策略,博弈主体双方在选择不同的策略行为时其期望收入可存在一定的差异。当审计政府如实申报而中央政府进行监管时,审计与中央政府的收益分别为B+RC-θW、αW-(B+C)R-I;当省级政府如实申报而中央政府不进行监管时,省级与中央政府的收益分别为B+RC-θW、αW-(B+C)R;当省级政府存在虚报而中央政府进行监管时,省级与中央政府的收益分别为DC-θW和αW-D(B+C);当省级政府存在虚报而中央政府不监管时。省级与中央政府的收益分别为B+DC-θW、αW-D(B+C)。中央政府的最优策略为在地方政府不存在虚报时为不监管、在地方政府存在虚报报时进行监管。而地方政府的最优策略为在中央政府不监管时存生虚报、在中央政府监管时不产生虚报。在选择不同策略时博弈双方主体以某种概率分布,存在一个浑河战略的纳什平衡,因此省级与中央政府在混合纳什平衡条件下的支付矩阵见表1。
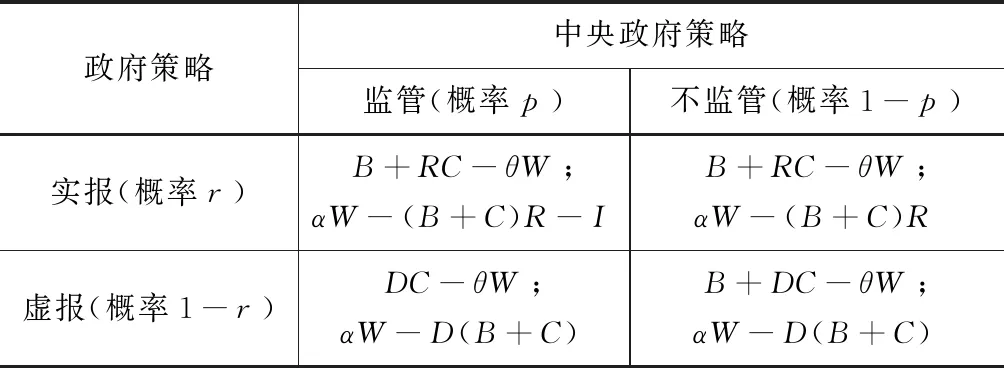
表1 地方与中央政府在混合纳什平衡条件下的支付矩阵
由上表可以看出,中央政府在选择监管与不监管时的期望收入分别如下:r[αW-(B-C)R-I]+(1-r)[αW-DC-I];r[αW-(B+C)R]+(1-r)[αW-D(B+C)];而省级政府在如实申报与存在虚报的期望收益分别为:p[]B+RC-θW]+(1-p)[B+RC-θW]和p[]DC-θW]+(1-p)[B+DC-θW]。
利用上述结果和混合纳什平衡基本理论可求得省级政府的监管概率和地方政府的实报概率分别为p*(p*=(D-R)C/B)和r*(r*=(DB-I)(DB);当符合p
1.2 省级政府与基层政府分摊模型
在基层与省级政府之间的分摊比例进行讨论时首先应假定按工程所辖人口中央进行定量补偿,并且考虑到基层与省级政府存在虚报部分并假定分摊比例与虚报分摊比例相同[11]。若分摊总额为1,则省级与基层政府的分摊分别为1-t和t,其中0≤t≤1。假定基层与省级政府的虚报资金分别为F2、F1,则申报部分减去实际需求资金即为总虚报部分资金,可表示为F1+F2=D-R,因此省级与基层政府的资金分摊与申报比例可表示为:
t/(1-t)=F1/F2
(1)
省级与基层政府在分摊比例模型中均知道自己决策行为对对方的反应函数,其中反应函数常数引入K1、K2进行表征,因此可求得基层与省级政府的期望资金申报函数,表达式如下:

(2)
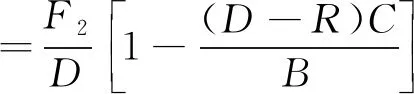
(3)
地方与省级政府依据博弈主体的利益最大化基本假定都希望自己具有最大的资金申报需求[12],因此省级与地方政府利用资金申报需求函数求导可求得各自的资金申报在期望资金申报函数的需求F2、F1,并具有显著的凹性,可存在最大值满足各自需求的利益最大化。在基层与省级政府的一阶最优化问题可表示为:
假定∂π省/∂F1=0;∂π基/∂F2=0,则有方程:
(4)
引入F2*、F1*分别代表基层与省级政府的资金最优虚报数,利用上述公式可求得各级政府的资金最优虚报需求,计算公式如下:
(5)
(6)
省级与基层政府的资金最优虚报需求F2*、F1*由于主体博弈的存在而不能同时达到要求,因此各级政府的资金最优虚报需求函数可依据公式(5)和(6)进行建立,如图1所示,双方的资金最优虚报需求即为之间的交点(F1**,F2**)。
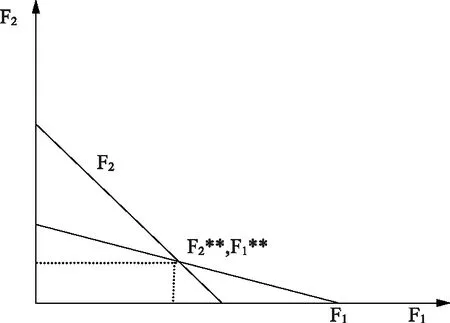
图1 省政府反映函数
据此可对省级与基层政府的资金最优虚报(F1**,F2**)进行求解,计算公式分别如下:
(7)
(8)
上述公式满足L1+=2WB+C2;L2=CB+C2R;L3=2WB+C(B+C);
L4=-C(B+C);L5=(B+C)(B+CR)。
利用上述结果可对分摊比例进行求解,公式如下:
(9)
2 实例应用
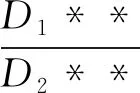
3 结论
(1)铁岭市区政府和县政府补贴分别为685.42万元和40.38万元,区政府、中央与省级政府资金补偿分别占总额的31.8%和68.2%;各级政府的分摊比例和补偿额具有一定的可实现性与合理性;其中县级政府为项目运行的责任主体并承担补偿费用的主要部分,省级与中央政府给予合理的分摊符合省级与中央的相关利益。
(2)本研究是在假定了中央政府补偿资金固定的前提下进行研究,因此在分摊比例计算时只是对基层与省级政府的分摊比例进行求解,而对中央补偿资金为变量的条件下各级政府的分摊比例仍需要进一步的研究。

