屏蔽电机氮气腔壁表面吸收率对温度场的影响
仲维滨,刘延浩,周 超,路义萍,谢增林
屏蔽电机氮气腔壁表面吸收率对温度场的影响
仲维滨1,刘延浩2,周 超2,路义萍2,谢增林1
(1. 哈尔滨电气动力装备有限公司,哈尔滨 150066;2. 哈尔滨理工大学机械动力工程学院,哈尔滨 150080)
核主泵屏蔽电机绕组的峰值温度高低直接关系到电机能否安全运行。本文针对某大型屏蔽电机,基于有限体积法,根据计算流体动力学(CFD)原理,考虑了定子端部氮气腔中辐射换热,并对腔壁表面吸收率的变化时电机内三维温度场进行了数值模拟,获得了主要部件的温度分布特点。计算结果表明,当氮气腔内壁面的吸收率由0.2提高到0.6时,电机的峰值温度降低了7.2%,强化辐射换热能够有效降低定子绕组的峰值温度。所得结论能为屏蔽电机中强化传热设计提供参考。
屏蔽电机;氮气腔内壁面吸收率;温度场;强化辐射换热;CFD
0 前言
以往在进行电机流-热耦合数值分析时,会忽略辐射换热,在计算模型中只考虑对流换热和导热两种热传递方法,这是目前电机温度场数值模拟比较常见的计算方式[1]。文章中所讨论的屏蔽电机主要使用在核电方面,上下端部氮气腔中绕组温度较高,是电机峰值温度所在处,辐射传热是该处的热传递方式之一,为保证电机60年安全运行,进一步降低峰值温度,探索强化该处的传热研究显得非常必要[2]。
国内外很多学者对各类屏蔽电机在电磁线圈处理、流体缝隙一般规律、产品设计与生产技术、使用可靠度等不同的层面[3-6]进行了大量研究;随着核主泵屏蔽电机的不断优化设计,鉴于试验的复杂性及滞后性,在研发阶段能够对所设计的电机进行流场、温度场的数值模拟研究[7-10],并对其内部件数值模拟计算方法及其影响因素进行三维仿真研究显得非常重要。此外,通过数值模拟的方式来研究各种规模较大的电机设计技术已经在以往的多次案例中被使用[11-13],试验研究虽然不能完全被数值模拟替代,但是这种方式能够表达出电机内部的相互作用原理以及物理规律的变化,因此能够为机电研究优化设计提供理论基础。
本文以一种屏蔽电机为研究对象,针对其内部损耗高,发热严重,特别是氮气腔内定子绕组端部结构,散热条件差,峰值温度十分接近绝缘的许用温度等问题[8-9],运用了流体力学(CFD)的计算方法,湍流选择使用剪切应力传输(SST)两方程模型研究,端部气腔必须要充分考虑到辐射,并且选取DO(Discrete Ordinate Methods)模型进行耦合计算;重点研究额定运行工况时,端部氮气腔中内壁面发射率变化对定子绕组最高温度的影响,研究分析降低绕组温度的可行性,以进一步保障电机的正常工作状态。
1 模型构建
本文中讨论的屏蔽电机主要指立体式鼠笼三相四极型异步屏蔽电动机设备,其正常工作时的转速是1786 r/min,绕组的绝缘级别约为N级,最大允许使用温度为200℃,定子的主要绕组方式采用双层短距绕组。屏蔽电机的冷却水路分为两部分,其中最主要的是电机内部的冷却水路,即一次冷却水路。外置换热器中的低温冷却水从下封头的入口管进入电机内,由电机转子轴内通道到达辅叶轮处;经过辅叶轮提速、加压后从出口甩出。辅叶轮出口处的冷却水又分为两路,一路向下回流,冷却下径向轴承、下飞轮及飞轮两侧的双向推力轴承,在下端盖内入口前与新的低温冷却水混合;另一路冷却水经过定、转子和屏蔽套之间环形通道,以对流换热的方式带走定、转子和屏蔽套中的热量,然后继续向上流动,冷却上推力轴承、上封头及上飞轮等部件,最终升温后的冷却水进入上封头的汇流腔中,从上封头出口管道进入外置换热器进行冷却,如图1所示。
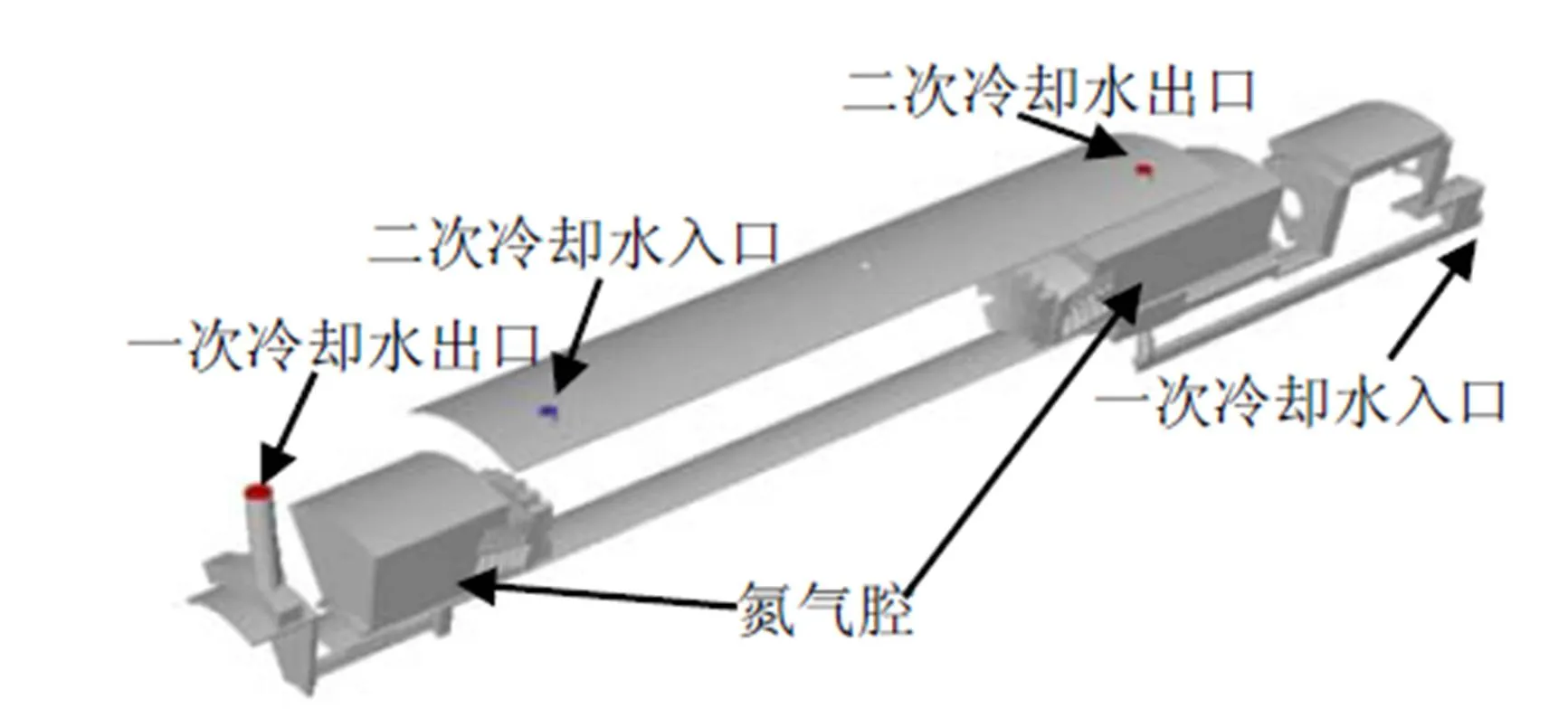
图1 电机冷却水路及氮气腔物理模型
考虑该电机内热量传递的连续性及几何布置特点,选取了整机周向1/8作为计算域物理模型,如图2所示。

图2 电机部件整体模型
2 数学模型及计算条件
2.1 基本假设
(1)电机内一、二次冷却水流动表现为湍流状态,而且流体的流动速度较为平稳,所以,应当按照湍流状态下的控制模型计算方式来进行电机流场数据计算;
(2)对电机的冷却液材料选择来说,其马赫数不超过1,因此可以将这种流体认为是不能够压缩流体,即是表示流体的密度不会由于压力的变化而发生改变;
(3)在稳态温度计算中,电机可看做为均质发热体,电磁的工作耗损以及水体运动摩擦过程中所产生的热能可以认为均匀分布于每个个体当中,所以能够按照热源密度情况来进行赋值计算;
(4)因为定、转子铁心是由硅钢片叠装而成,横、纵向导热系数差异较大,所以物性参数为各向异性,其他材料为各项同性;
(5)进行辐射热能的相关计算时,可以将氮气腔内部的部件(如定子压板、锥形环、支撑环等)材料设定为与灰体具有相似的性质,其发射频率和主要的吸收频率都完全一致,并且气腔内的不同位置拥有一样的吸收率,数值为0.2[14];
(6)辐射换热计算过程中,认为定子的绕组绝缘材料为灰体,其发射频率和吸收频率一致,都是0.4[14]。
2.2 数学模型
冷却介质水密度是常数,冷却介质处于湍流情况。因此在计算过程中,需要充分认识到因转子的转动过程带动屏蔽套间隙里的水旋转,并且处于主轴中的水也会随着主轴转动,因此是复杂三维空间内多坐标系下的流动、传热问题,需要设定出一定的旋转速度下的旋转壁面。其稳定状态和传热状态使用基本相同的控制方程来进行计算,包括质量、动量、能量守恒方程[13]:

在屏蔽电机的顶部与底部位置的封闭空腔内部的氮气和邻近区域的线棒以及其余的固体表面发生的主要是自然状态下的对流方式热量交换,这种换热形式的热量转移速度主要是由交换双方之间的温度或者密度差大小造成的;在空腔内部远离壁面的区域,不存在驱动力,因此只需要按照自然对流来进行考虑,并且由于氮气微观结构为双原子,基本属于透明介质类型,在热量交换的过程对热量的吸收能力为0,如果考虑到辐射形式的热量交换,那么需要在方程(1)的右侧散度区域内增加辐射换热转子转动时由于黏性作用带动冷却水流动,冷却水路在径向上尺寸较小,特别是在屏蔽套之间的冷却水路,会在径向上形成较大的速度梯度层,属于边界层内受黏性力支配的绕圆柱强制对流。考虑各种湍流模型特点,在Fluent软件中,选用SST模型计算流场。同时,进行温度场计算时,选用DO辐射模型耦合计算,具体见文献[15],最终获得收敛解:
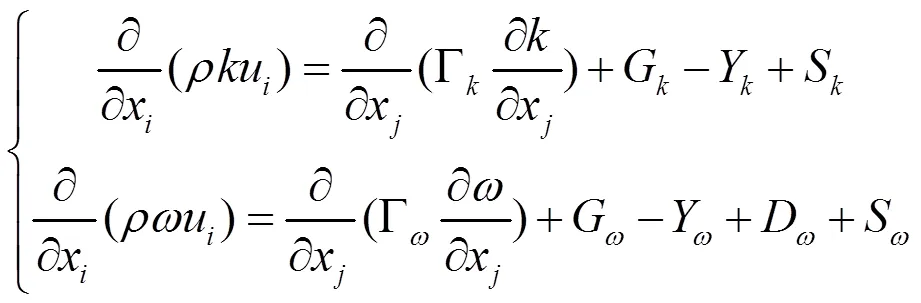
式中,S和S主要表示为自定义源项,G主要代表因为平均速度变化而造成的湍流动能,G表示数学函数造成的湍流状态动能变化。
2.3 计算条件
对于流体流动和传热相关问题的研究中需要首先限定边界、热源以及热物性等,本文所研究的问题的边界条件如下:
(1)计算域一、二次冷却水入口为速度入口,试验测得速度数值分别为4.66m/s、1.74m/s,温度数值分别为57°C、37.8°C;一、二次冷却水出口表压力均为0Pa。
(2)屏蔽电机定子端部绕组采用渐开线型的几何结构,计算域左右两侧边界上(1/8计算域物理模型,周向-22.5°和22.5°为边界面)的绕组截面对应设置为周期性边界;物理模型上部,表示处于上面的飞轮的地面处于恒温状态下;其他的电机和空气自然接触情况下的对流换热定义换热系数为基本的1W/(m2·K),而机器的工作环境的温度定义为48.9℃。处于电机内部的冷却水与周边的壁体之间的边界条件为流固耦合状态,电机内部的转子位置壁体表面类同于处于旋转坐标体系状态中,定义其转速为1786r/min。
(3)假设热源均布于发热体中。电机额定电流下,转子部分包括铁心、屏蔽套体、环耗损、谐波耗损以及铜耗,定子部位主要包括有铁心与铜耗等,定转子铁心齿部与轭部的能力损耗需要另外进行计算,除上述所说之外还必须要对锥形环与定子齿压板、轭部等位置的损耗进行充分考虑,这些部位的损耗情况除了采用不同的分析软件进行计算之外,还可以参考厂商提供的数据值;其杂散损耗在充分研究和分析了厂商提供的同类别的屏蔽电机数据基础上根据已有经验按照不同的比例进行分配,假设损耗均匀分布在发热体中。电机内部的水路里,辅助叶轮、定转子外部所装屏蔽套、顶部与顶部的导轴承以及上下飞轮部位的流体的厚度较薄,一般采用毫米为数量单位,并且其中具有明显的机械磨损,通常根据解析法来分析和计算工作状态下的水摩擦能量耗损,可以在流体中设置完全一致的水体作为热源项来进行分析[7-9]。
(4)关于热物性条件,经多次模拟计算以后,材料的热物性参数应当设置为这种材料的升温数值中的最小项。并且,定转子的铁心叠片一般认为是各向异性的传热材料,其轴向与径向、切向的对应数值需要根据试验结果来进行确定,其余部位基本认为是各向同性,可以根据常规材料来确定数值大小。其中,定子绕组绝缘表面的发射率为0.4。
当对求解域内部的流场与对应温度场进行分析与计算时,需要进行多次重复试算,并且需要对各次结果进行Y+优化,这样才能够使结果充分符合壁面函数的需要;微分计算方程中的对流项目离散通常按照二阶迎风式来进行分析,使用分离式方程组、隐式来计算最终结果,一般根据SIMPLE算法来对压力耦合方程组进行计算,结果方程组求解能够得到速度与温度场耦合收敛形式的网格独立解。
3 温度场计算结果与分析
根据屏蔽电机内湍流状态下的流场与温度场相互耦合计算结果,在定子绕组绝缘表面的发射率均为0.4,定子端部氮气腔中内壁面发射率为0.2、0.6可通过改变金属表面颜色、表面氧化等多种方法增强腔壁的吸收率[14](本文中不做详细研究)。两种条件下,得到考虑辐射换热时计算域内的温度分布特征。
3.1 定子氮气腔内壁面吸收率为0.2时温度分布特征
图3给出了计算域物理模型中的三维温度分布云图,图中温度分布特征为:定子外夹套的设备冷却水温度最低,云图显示数值为37.8℃;定子绕组上端部温度最高,云图显示数值为182.1℃。
定子绕组温度的最高值不能够大于定子的绝缘允许温度值,绕组整体沿轴向呈现出中部温度低、两侧温度高的变化形式;并且沿着半径方向温度呈现减小的趋势。绕组上端部受上飞轮温度及一次冷却水流动方向的影响,导致上端部温度略高于下端部。定子绕组在整个计算模型中温度最高,原因之一是损耗较大,原因之二为在氮气腔内部,绕组两端主要是因为氮气与壁表面自然对流连同氮气间导热,绕组表面与可见的腔壁面间的辐射换热向与之不接触的腔内壁表面传热,传热环节较多,特别是通过氮气介质导热环节,由于其热导率很小,散热效果很差(端部腔必须采用惰性气体)。所以为保证电机安全稳定运行,强化辐射传热必然成为降低定子绕组峰值温度的一种重要措施。

图3 计算域内部温度分布云图/℃
3.2 定子绕组温度分布比较
为比较方便,图4与图5给出了氮气腔内壁面吸收率分别为0.2、0.6,其他条件完全相同时定子绕组部件的三维温度分布云图。对比可知,氮气腔内壁面吸收率为0.6时,上端部的最高温度为169.9°C,与绝缘许用温度200°C相差约30°C,安全余度增加,比吸收率为0.2时降低了7.2%,与吸收率为0.2时的试验测量峰值温度186°C相比,温度降低了8.7%;下端部的绕组最高温度也降低14.8°C。说明增强绕组绝缘表面和腔壁之间的辐射换热强度能够有效地降低定子绕组的温度,同时证明本文计算结果误差较小,吸收率为0.2时的峰值误差为-2.1%。此外,绕组鼻端同一轴向截面位置的温度差变大,中心层绕组温度数值最高,云图显示更为明显,这是因为高温定子绝缘外表面热量以热辐射方式向外界投射,到达氮气腔内低温壁面热量被吸收的份额增加,导致其温度降低,与定子绝缘外表面相邻的内层绕组间产生温差,向外层的导热量也相应增加。绕组直线段部分的最低温度也由81.4°C降低为80.5°C。
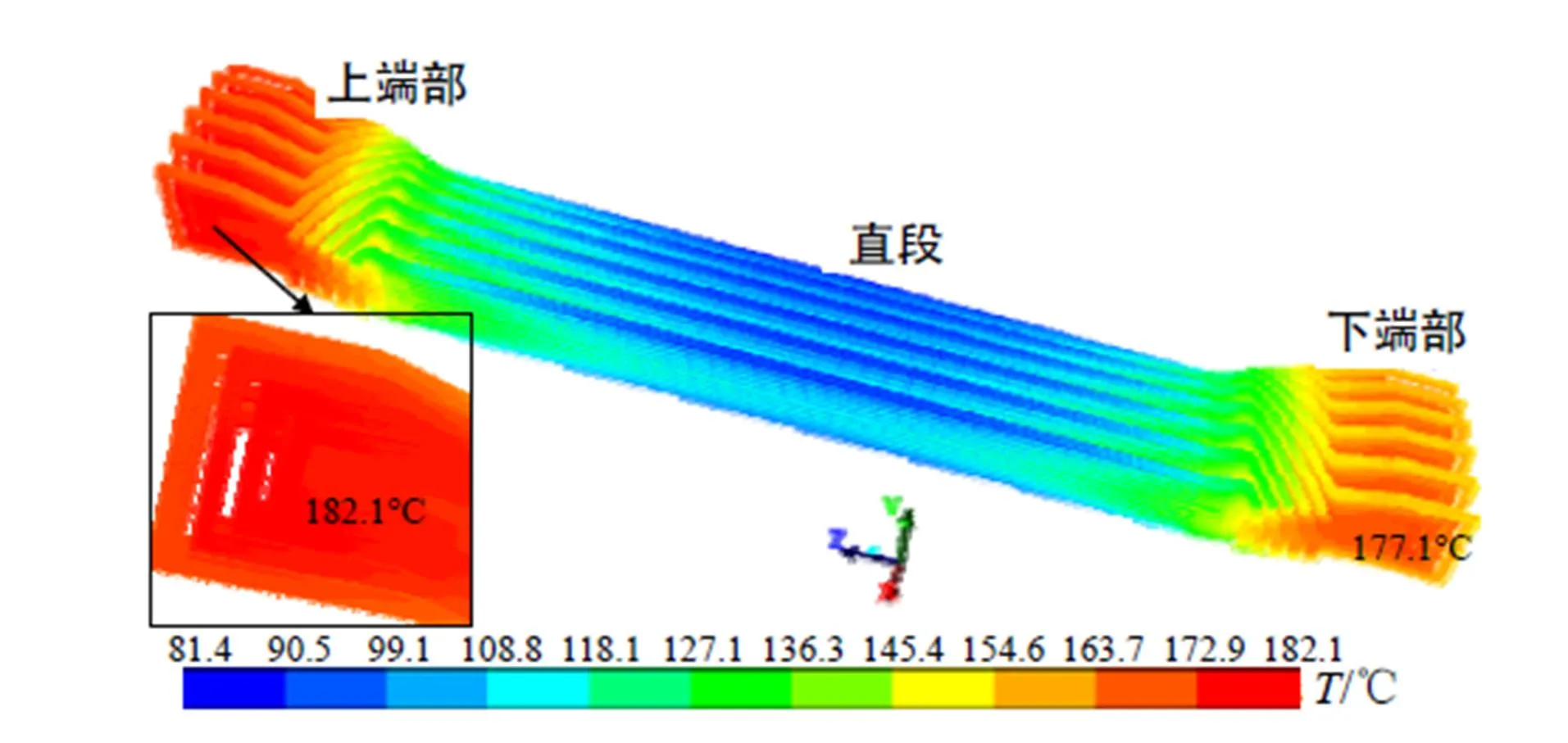
图4 吸收率0.2时定子绕组温度分布云图/℃
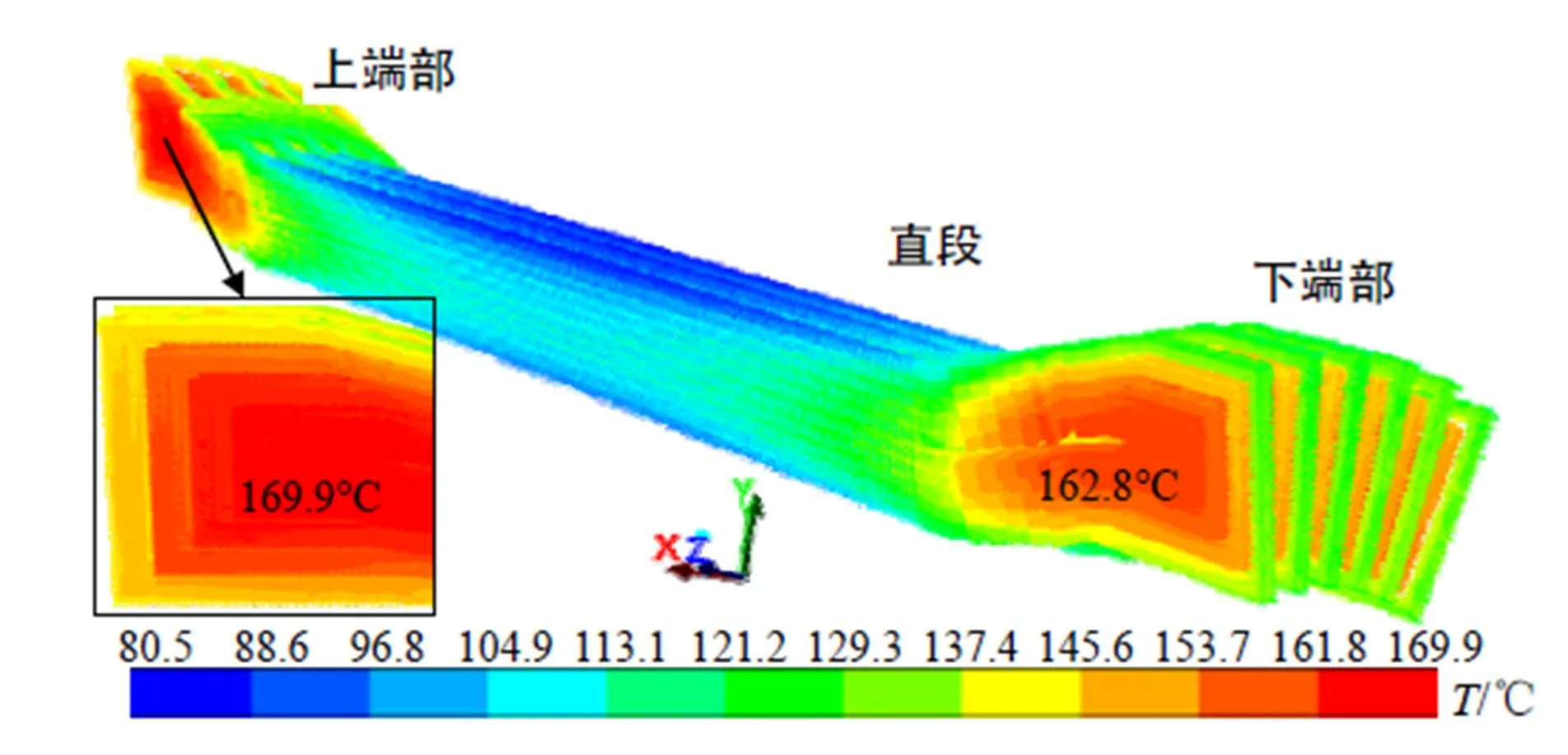
图5 吸收率为0.6时定子绕组温度分布云图
3.3 相邻部件温度分布特征
为了说明定子腔内壁吸收率变化对主要部件温度分布的影响,图6、7分别给出了氮气腔内壁面吸收率为0.2时定子铁心和定子上、下压板的温度分布云图,为比较方便,图8给出了内壁面吸收率为0.6时定子铁心和定子上、下压板的温度分布云图,(a)为定子铁心,(b)为定子上、下压板。对比三幅图可以看出,增强氮气腔壁的吸收率之后,定子铁心和上、下压板的温度分布规律不变,齿部温度高,轭部温度低,轭部沿半径增大方向温度逐渐降低,形成明显温度梯度。铁心的最高温度依然出现在铁心齿部上端面,但温度数值降低,铁心的最高温度降为129.7°C,上、下压板的最高温度为129.6°C和124.9°C,比原吸收率情况下分别降低了3.7°C、3.5°C和5°C,温度变化不明显。
屏蔽电机内的辐射换热主要发生在氮气腔中,发生于定子绕组端部绝缘表面与氮气腔壁之间,辐射换热对电机温度场的影响主要在定子绕组端部区域,对其他部分以及流场影响很小。

图6 吸收率0.2时定子铁心温度分布云图
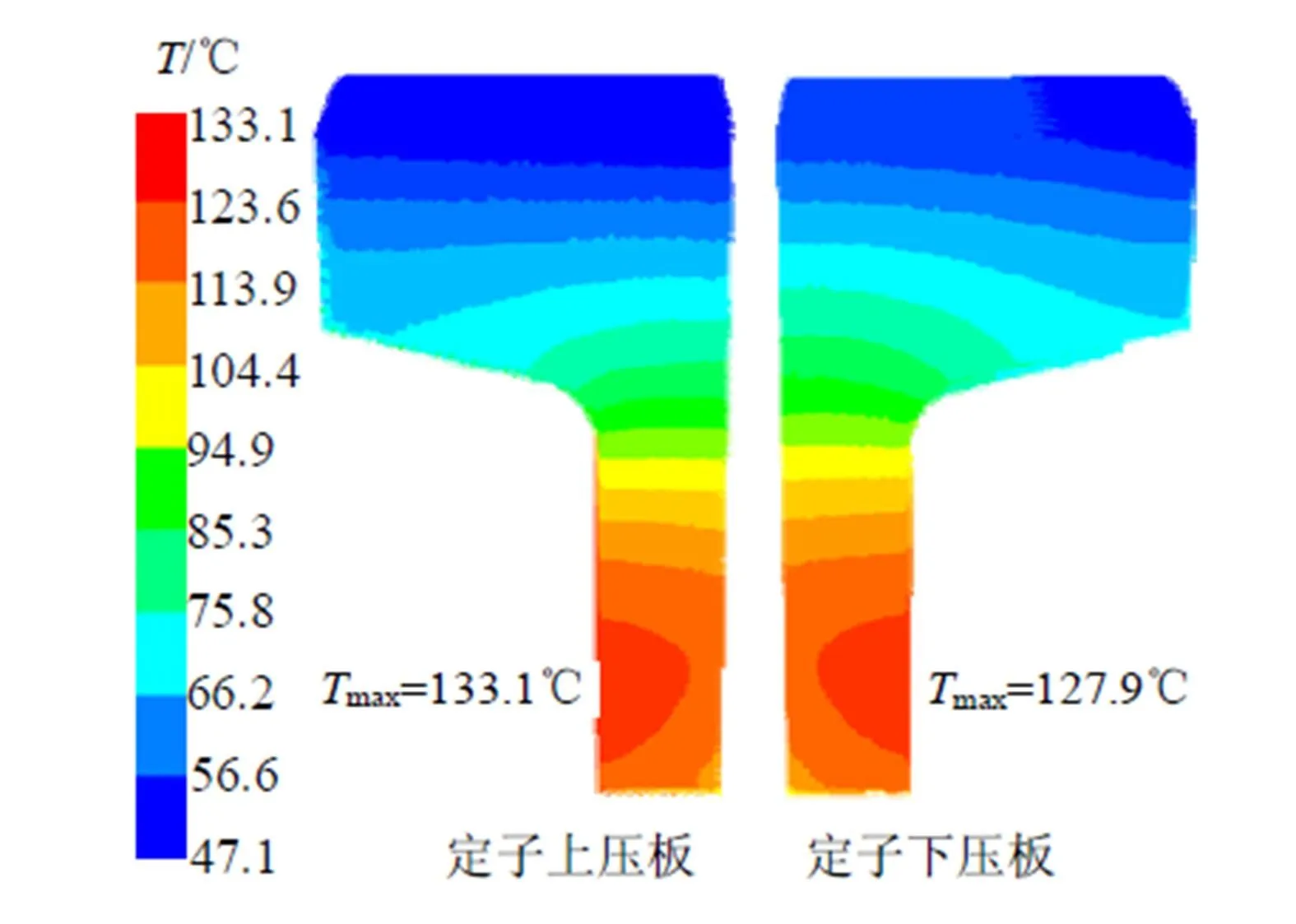
图7 吸收率0.2时定子压板温度分布云图

图8 定子铁心和压板温度分布云图(吸收率0.6)
4 结论
本文以一台屏蔽电机为例,对屏蔽电机定子端部腔表面发射率变化对温度场影响进行了CFD数值模拟研究,得到结论如下:
将腔壁的吸收率由0.2提高到0.6之后,增强氮气腔内辐射换热,能够改善屏蔽电机定子绕组的温度分布,绕组的峰值温度降低7.2%,其他各部件的平均温度降低不明显;有利于提高电机寿命,保障电机的安全运行。
[1] 陈起旭,王云洪,杨来顺,徐俊,曹秉刚. 通转子三相异步电动机温度场流场耦合分析[J]. 电机与控制应用, 2017, 44(10):77-82.
[2] 丁舜年.大型电机的发热与冷却[M].北京: 科学出版社, 1992:136-175.
[3] 宋艳文,林艳江.屏蔽电动机屏蔽套的设计特点及常见问题的预防措施[J]. 防爆电机, 2002,(110):16-18.
[4] 罗宇辰,刘应征,陈汉平. 压水堆主泵飞轮周围间隙流中泰勒涡传热特性的数值研究[J].原子能科学技术,2014,48(3):441-446.
[5] 孙桂英,邹继斌,李连锋,等. 屏蔽电机的磁场与屏蔽层损耗的解析计算[J]. 哈尔滨工业大学学报, 1999, 31(4):30-33.
[6] LIANG Y P, BIAN X, YU H H, et al. Finite-Element Evaluation and Eddy-Current Loss Decrease in Stator End Metallic Parts of a Large Double-Canned Induction Motor[J]. IEEE Transactions on Industrial Electronics, 2015, 62(11):6779-6785.
[7] 丁树业, 孟繁东, 葛云中. 核主泵屏蔽电机温度场研究[J]. 中国电机工程学报, 2012, 32(36):149-155.
[8] 李藏雪,任智达,路义萍,等. 一种屏蔽电动机的三维温度场及影响因素研究[J].电机与控制学报,2015,19(8):15-21.
[9] 霍菲,张晓晨,程鹏.屏蔽电机定子温度场的数值计算与分析[J]. 电机与控制应用, 2006(4):7-12.
[10] 谢增林.双屏蔽电机屏蔽套材料对定子绕组温度的影响[J]. 机电信息, 2016(18):165-167.
[11] 李俊卿,马少丽,李和明. 基于耦合物理场的汽轮发电机定子温度场的分析与计算[J]. 华北电力大学学报, 2008, 33(5):6-10.
[12] 周封,熊斌,李伟力,程树康. 大型电机定子三维流体场计算及其对温度场分布的影响[J].中国电机工程学报,2005,25(24):128-132.
[13] Lu Yiping, Liu Li, Zhang Dongxue. Simulation and Analysis of Thermal Fields of Rotor Multislots for Nonsalient-Pole Motor [J]. IEEE Transactions on Industry Electronics,2015,62(12):7678-7686.
[14] 余其铮.辐射换热原理[M] .哈尔滨:哈尔滨工业大学出版社,2000:26-68.
[15] Fluent Inc. (2017). Fluent 18. User’s Manual. Fluent Inc, USA.
Influence of Wall Absorptivity in Nitrogen Cavity on the Temperature Field of Canned Motor
ZHONG Weibin1, LIU Yanhao2, ZHOU Chao2, LU Yiping2, XIE Zenglin1
(1. Harbin Electric Power Equipment Co., Ltd., Harbin 150066, China; 2. School of Mechanical Power Engineering, Harbin University of Science and Technology, Harbin 150080, China)
The peak temperature of winding in Nuclear main pump shield motor is directly related to the safety of the motor. For a large canned motor structure, based on the finite volume method, according to the principle of computational fluid dynamics (CFD), the numerical simulation of the internal temperature field of the motor is adopted considering radiation heat transfer and variation of wall aborptivity. A three-dimensional temperature fields of the canned motor are obtained. The calculation results show that the peak temperature of the motor is reduced by 7.2% when wall absorptivity in nitrogen cavity is increased from 0.2 to 0.6. Intensifying the radiation heat transfer can effectively reduce the peak temperature of the stator winding. The conclusions provide a reference for the canned motor heat transfer enhancement design.
canned motor; wall absorptivity in nitrogen cavity; temperature field; enhanced radiative heat transfer; CFD
TM343
A
1000-3983(2018)06-0062-05
2018-04-12
仲维滨(1963-),1985年7月毕业于吉林工业大学机械制造专业,2010年5月毕业于清华大学工商管理专业,硕士,主要从事科研、设计、制造、检验试验、管理等工作,高级工程师。


