多塔部分斜拉桥自振频率的实用简化算法

唐冕，丁千夏，宋旭明



多塔部分斜拉桥自振频率的实用简化算法

唐冕1，丁千夏2，宋旭明1

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 华蓝设计(集团)有限公司，广西 南宁 530011)

为了便于在概念设计阶段快速准确地估算多塔部分斜拉桥的基频，根据Rayleighmethod方法，以主梁的静挠度曲线作为振型函数，推导支承体系和刚构体系多塔部分斜拉桥的基频估算公式。以某三塔部分斜拉桥为例，计算其频率，讨论结构体系及塔跨数对多塔部分斜拉桥基频的影响。并将公式与较为精确的有限元法和《公路桥涵抗风设计规范》的单一估算方法进行比较，研究结果表明：计算多塔部分斜拉桥基频不可忽略结构体系及塔跨数的影响；支撑体系基频远低于刚构体系，不可用单一公式计算；随着塔跨数增加，基频降低。有限元解与公式解的对比结果表明，公式基频误差在10%以内，可以满足工程概念设计的需要。

斜拉桥；基频；矮塔；结构体系

部分斜拉桥作为连续梁(或连续刚构)与斜拉桥的组合体系，具有塔矮、梁刚、索集中的特点，灵活的跨径布置、美观的外形及经济的造价使其在近年内得到广泛应用。目前的《公路斜拉桥设计细则》和《公路斜拉桥抗风设计规范》中仅对双塔斜拉桥中有辅助墩和没有辅助墩有不同的估算公式，没有考虑各种边界条件，对于与普通斜拉桥不同的多塔部分斜拉桥没有明确区分。根据国内外众多学者对斜拉桥实时监测数据和数值模拟的研究，斜拉桥的动力特性除了受结构自身状态的影响外，还收到各种温度、损伤和车辆荷载质量等环境因素的影 响[1−6]。为了研究斜拉桥的动力特性，陈恒大等[7]推导了考虑主塔刚度影响三塔斜拉桥振动基频公式；李国豪[8]用单质点模型来估算漂浮体系斜拉桥基频；袁万城等[9]用双质点模型估算斜拉桥的纵飘频率；张先忠等[10]提出名义单位质量的抗弯刚度概念，推导高墩固结体系矮塔斜拉桥纵飘基频的估算公式；宋涛等[11]假设振型函数为三角函数，用Rayleigh method法，推导双塔矮塔斜拉桥基频。对于支承体系斜拉桥，本文简化为简支梁模型，对于刚构体系斜拉桥简化为固端梁模型，以静挠度曲线作为振型函数，并考虑了多塔的影响，推导斜拉桥基频，并与相对精确的有限元法和《公路桥涵抗风设计规范》的估算方法进行比较。

1 Rayleigh method法计算斜拉桥基频

1.1 斜拉桥基频的推导

用Rayleigh method计算斜拉桥的频率基本公式为：

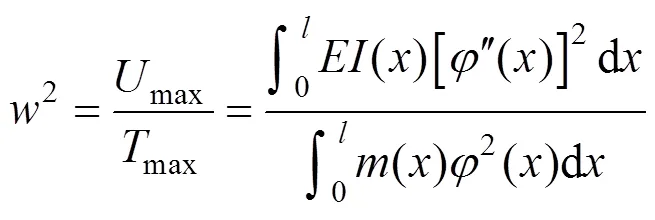
其中：势能和动能都包括主梁、主塔和拉索3部分。

主梁弯曲变形能为：

主塔弯曲变形能为：

考虑主塔的侧向位移，拉索的变形量示意图如图1所示。

(a) 主塔侧向位移；(b) 主梁挠度

则拉索的变形量为：

其中：为主梁在拉索处的挠度；为桥塔侧向 位移。

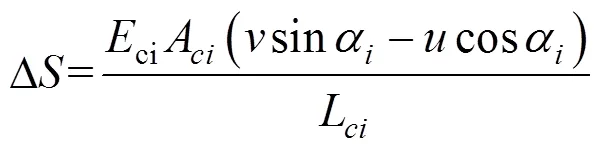
式中：Δ为拉索索力增量；E和A为拉索的弹性模量和截面面积；和L为拉索的水平倾角和 索长。

拉索的变形能为：

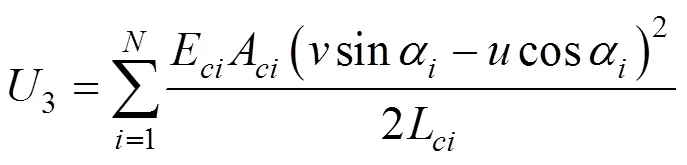
其中：为拉索数。

索力垂直分量的变化为：

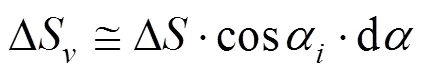
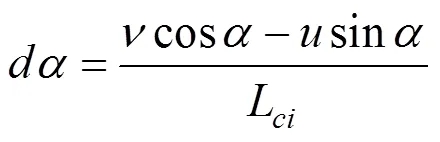
二次变形所做的功为：

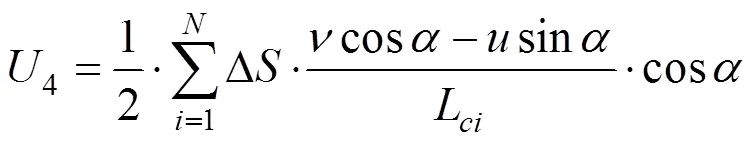
主梁动能为：

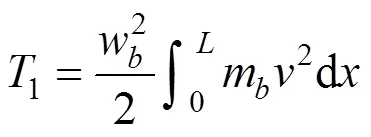
主塔动能为：

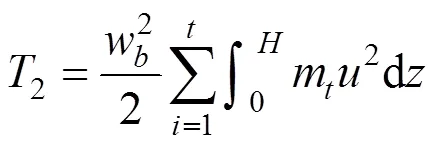
拉索动能为：

把式(2)，(3)，(6)，(9)~(12)代入式(1)得：

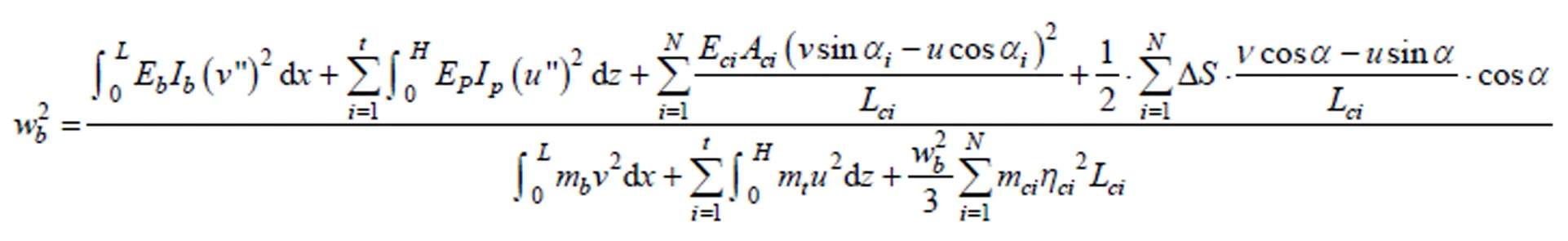
1.2 斜拉桥基频的简化

在动能中，拉索质量相对主梁质量是个小量，可以忽略或者合并到主梁质量中，并且拉索的动力特性与分析阻尼器、梁体振动、温度等外界条件有关[12]，分析较为繁杂，因此本文不计算拉索动能。主塔的变位和质量相对于主梁也是小量，桥塔截面抗弯刚度仅对高阶频率有明显影响[3]，本文也忽略不计。在弯曲变形能中，拉索的二次变形能相对较小，可以忽略不计[7]，则(13)式简化为：

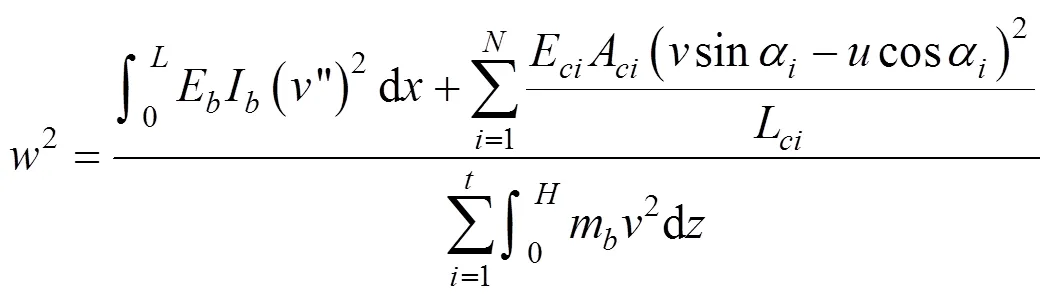
2 部分斜拉桥基频

2.1 支承体系

由式(14)求频率，必须先假定振型函数，假定的振型函数越接近第一阶实际振型函数时，得到的基频就越精确。因为支承体系是将主梁支承在墩上，主梁一般只在一个塔柱处设置固定支座，其余为纵向活动支座。因此，把支承体系斜拉桥主梁简化为均布荷载作用下的简支梁，取其均布荷载下的静挠度曲线作为振型函数：

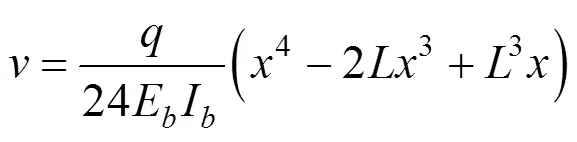
求导得：

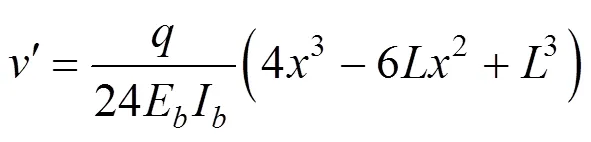
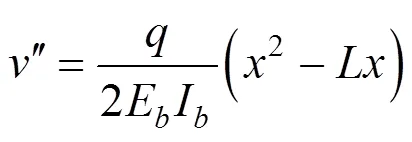
把式(17)代入式(2)得：

把式(11)代入式(6)得：

忽略塔的侧向位移，主梁跨中最大挠度为：

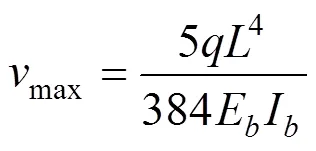
以平均挠度计算拉索的变形能，即：

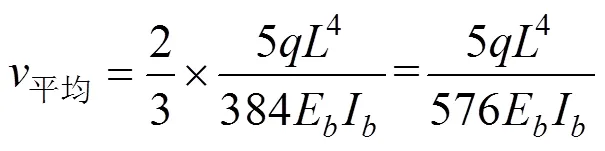
则单根拉索的变形能为：

则拉索变形能为：

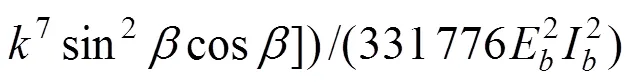
式中：为主塔每侧拉索数；为中跨拉索倾角；为边跨拉索倾角。

把式(18)，(19)和(23)代入式(14)得：

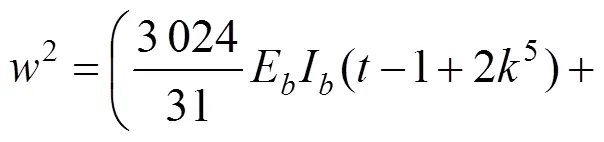
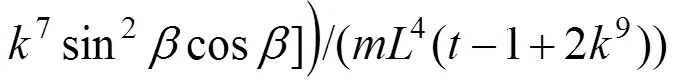
2.2 刚构体系

因为刚构体系斜拉桥塔梁墩相互固结，形成具有多点弹性支承的刚构。因此，把刚构体系斜拉桥主梁简化为均布荷载作用下的固端梁，取其均布荷载下的静挠度曲线作为振型函数。

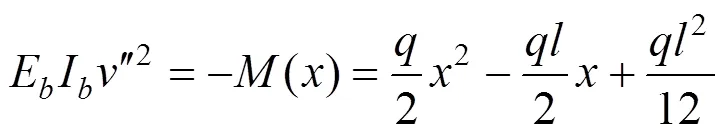
积分得：

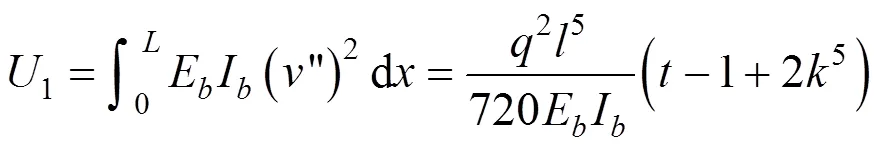
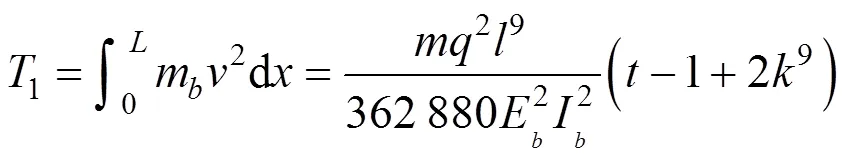
以平均挠度计算拉索的变形能，即：

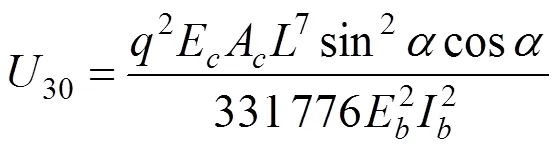
式中：为主塔每侧拉索数；为中跨拉索倾角；为边跨拉索倾角。

则拉索变形能为：

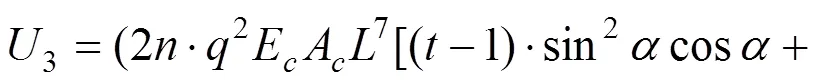
把式(27)，(28)和(32)代入式(14)得：

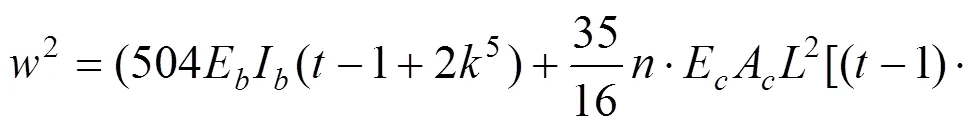
综上所述，支承体系多塔部分斜拉桥，刚构体系多塔部分斜拉桥基频可用下式计算：

支承体系：

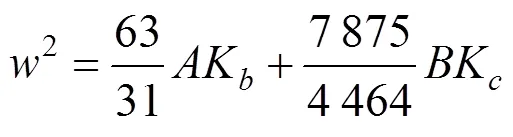
刚构体系：

其中：

若=：

3 算例分析

以某在建的三塔矮塔斜拉桥为基准模型，采用Midas civil 2015进行仿真分析，通过变换结构体系或塔跨数，来对比不同结构体系及不同塔跨数下的桥梁动力响应。中跨跨径225 m，主梁刚度EI=2.59×109(kN∙m2)，拉索刚度EI=1.5×106kN，边中跨比为0.62，主梁单位长质量=82.0 (mg∙m−1)，主塔每侧拉索数=18，倾角0.317 rad。桥型布置图如图2所示。

表1，表2和表3中的基频均为竖弯基频。表1和表2数值分析结果表明，随着塔跨数增加，支承体系斜拉桥基频和刚构体系斜拉桥的基频均逐渐降低，与规范解的偏差也越来越大，但塔跨数增加的越多，基频降低的趋势越不明显。这是由于中塔没有后锚索，整体刚度比较小，因此塔跨数越多，多塔部分斜拉桥刚度越小，基频也越小。显然，斜拉桥的基频仅用跨径来计算是不够的，表1(表2)4个模型，跨径及其他计算计算参数都相同，但由于塔跨数不同，基频不同。

表3数值分析结果表明，采用支承体系的部分斜拉桥由于在纵桥向与横桥向约束大大减弱，所以基频明显较刚构体系要小得多。这也同样说明斜拉桥的基频仅仅用跨径来计算是不够的，故《公路桥梁抗风设计规范》的公式误差比较大，尤其对于支承体系斜拉桥。而宋涛等[5]以三角函数为振型函数，用瑞莱法推导的基频公式，三塔四跨支承体系斜拉桥计算基频为0.559 6 Hz，与有限元的值相比，误差也较大。而本文推导的基频公式计算误差都在10%以内，更加接近精确解，可以作为概念设计阶段的基频估算公式。

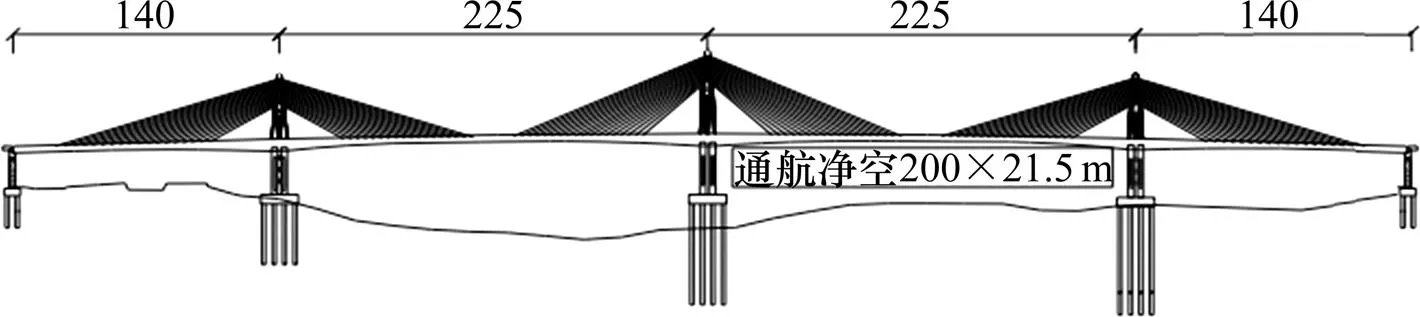
单位：m

表1 塔跨数对支承体系斜拉桥基频影响

注：误差1是规范解与有限元解之间的误差；误差2是规范解与有限元解之间的误差

表2 塔跨数对刚构体系斜拉桥基频影响

注：误差1是规范解与有限元解之间的误差；误差2是文中解与有限元解之间的误差

表3 结构体系对斜拉桥基频影响

注：误差1是规范解与有限元解之间的误差；误差2是文中解与有限元解之间的误差

4 结论

1) 随着塔跨数增加，斜拉桥基频降低；但是塔跨数增加地越多，基频降低地越不明显，因此塔跨数对多塔矮塔斜拉桥基频的影响不能忽略。

2) 支承体系基频远低于刚构体系基频，因此多塔矮塔斜拉桥基频，不仅与主梁抗弯刚度，拉索抗弯刚度，主跨跨径有关，结构体系对斜拉桥基频有很大影响。

3) 本文推导的式(34)~(35)适用于多塔支承体系斜拉桥和多塔刚构体系斜拉桥，而且与抗风规范和参考文献[5]和[6]相比更贴近Midas计算的精 确解。

[1] SONG M T, CAO D Q,ZHU W D, et al. Dynamic response of a cable-stayed bridge subjected to a moving vehicle load[J]. Acta Mechanica, 2016, 227(10): 2925−2945.

[2] Gwanghee Heo, Joonryong Jeon. Dynamic characteristics estimation of cable-stayed bridge using artificial filter bank (AFB)[J]. International Journal of Engineering and Technology, 2015, 7(1): 8−11.

[3] Bhagwat M, Sasmal S,Novák B, et al. Dynamic performance evaluation of straight and curved cable- stayed bridges[J]. Bridge Structures, 2009, 5(2−3): 87− 95.

[4] ZHOU Ding, JI Tianjian. Dynamic characteristics of a generalized[J]. International Journal of Mechanical Sciences, 2008, 50(1): 30−42.

[5] 闫涛. 基于监测数据的斜拉桥动力特性分析及基准模型研究[D]. 上海: 同济大学，2013: 77−87. YAN Tao. Study on dynamical properties and baseline model of cable-stayed brideg based on monitoring data[D]. Shanghai: Tongji University, 2013: 77−87.

[6] 关进轩. 多塔部分斜拉桥的参数敏感性分析及优化[D].长沙: 中南大学, 2016: 19−20. GUAN Jinxuan. Parameters sensitivity analysis and optimization of multi-pylon extra dosed cable-stayed bridge[D]. Changsha: Central South University, 2016: 19−20.

[7] 陈恒大, 邬晓光, 姚丝思, 等. 考虑主塔刚度影响的三塔斜拉桥振动基频实用公式[J]. 铁道科学与工程学报, 2016, 13(10): 1962−1969. CHEN Hengda, WU Xiaoguang, YAO Sisi, et al. Practical vertical frequency formula for vibration of cable-stayed bridges with three tower considering tower stiffness influence[J]. Journal of Railway Science and Engineering, 2016, 13(10): 1962−1969.

[8] 李国豪. 桥梁结构稳定与振动(修订版)[M]. 北京: 中国铁道出版社, 2002: 390−396. LI Guohao. Stability and vibration of bridge structure[M]. Beijing: China Railway Press, 2002: 390−396.

[9] 袁万诚, 闫冬. 斜拉桥纵飘频率简化计算方法[J]. 同济大学学报(自然科学版), 2005, 33(11): 1423−1427. YUAN Wancheng, YAN Dong. Simplified calculational method of floating frequency for cable-stayed bridges[J]. Journal of Tongji University (Natural Science Edition), 2005, 33(11): 1423−1427.

[10] 张先忠, 张筱雨, 宋涛. 高墩固结体系矮塔斜拉桥纵飘基频的估算实用公式[J]. 武汉大学学报(工学版), 2017, 50(3): 436−440. ZHANG Xianzhong, ZHANG Xiaoyu, SONG Tao. Estimation practical frequency formula for longitudinal vibration of frame rigid extradosed cable-stayed bridge with high pier[J]. Journal of Wuhan University Engineering, 2017, 50(3): 436−440.

[11] 宋涛, 宋一凡, 贺拴海, 等. 矮塔斜拉桥竖弯频率的能量法估算适用公式[J]. 北京工业大学学报, 2016, 42(4): 521−526. SONG Tao, SONG Yifan, HE Shuanhai, et al. Estimation practical frequency formulas for vertical vibration of extradosed cable-stayed bridge based on energy method[J]. Journal of Beijing University of Technology, 2016,42(4):521−526.

[12] 吉伯海, 程苗, 傅中秋, 等. 基于振动频率法的斜拉桥索力测试影响因素[J]. 中南大学学报(自然科学版), 2015, 46(7): 2621−2625. JI Bohai, CHEN Miao, FU Zhongqiu, et al. Influential factors in cable force measurement of cable-stayed bridges based on vibration frequency method[J]. Journal of Central South University (Science and Technology), 2015, 46(7): 2621−2625.

[13] 黄斌, 李烨君, 朱礼平, 等. 桥塔抗弯刚度随机性对斜拉桥动力特性的影响[J]. 西南交通大学学报, 2014, 49(2): 202−207. HUANG Bin, LI Yejun, ZHU Liping, et al. Effects towers random sectional bending stiffness on dynamic characteristics of large-span cable-stayed bridge[J]. Journal of Southwest Jiaotong University, 2014, 49(2): 202−207.

The practical simplification algorithm of multi-pylon extradosed cable-stayed Bridge fundamental frequency

TANG Mian1, DING Qianxia2, SONG Xuming1

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. Hualan Design Co., Ltd, Nanning 530011, China)

In order to estimate the fundamental frequency of multi tower cable-stayed bridge quickly and accurately in the conceptual design stage, this paper according to the Rayleigh method, took the static deflection curve of the main beam as the shape function, deduced the fundamental frequency estimation formula of the supporting system and rigid frame system of multi tower partial cable-stayed bridge. Taking a three towers partial cable-stayed bridge as an example, discuss the effect of structural system and tower number on the fundamental frequency of cable stayed bridge. Finally, the formula was compared with a more accurate finite element method and the single estimation method in “highway bridge wind resistant design specification”. The results show that the influence of structural system and tower number can’t be ignored in calculating the frequency of multi tower partial cable-stayed bridge: the frequency of support system is far lower than the rigid system, indicating a single formula is not accurate; with the increase in the number of towers, the frequency is reduced. The comparison results of the finite element solution and the formula shows that the error of the formula is less than 10%, which can satisfy the need of engineering concept design.

cable-stayed bridge; the fundamental frequency; short tower; the structural system

10.19713/j.cnki.43−1423/u.2018.11.017

U448.27

A

1672 − 7029(2018)11 −2861− 06

2017−09−14

国家自然科学基金资助项目(51178471，50908232)；湖南省交通科技资助项目(201426)

唐冕(1970−)，女，辽宁开原人，副教授，博士，从事大跨度复杂桥梁研究；E−mail：tangmian513@163.com

(编辑 蒋学东)